模拟单链表
拿捏链表一
-
- 一、单向、不带头、非循环链表的结构
- 二、代码实现
- 三、框架分析
-
- 0. 对框架进行说明
- 1. 创建一个类 Node,表示节点
- 2. 模拟链表内部结构
- 3. 初始化一个链表
- 4. 打印每个节点对应的 val
- 5. 得到链表的长度
- 6. 头插法
- 7. 尾插法
- 8. 在任一位置插入节点
- 9. 查找关键字key是否在单链表当中
- 10. 删除第一次出现关键字为 key 的节点
- 11. 删除所有出现 key 的节点
- 12. 清空链表
- 四、测试程序
-
- 1. 初始化链表
- 2. 插入功能
- 3. 删除单节点
- 4. 删除指定的重复节点
- 总结
一、单向、不带头、非循环链表的结构
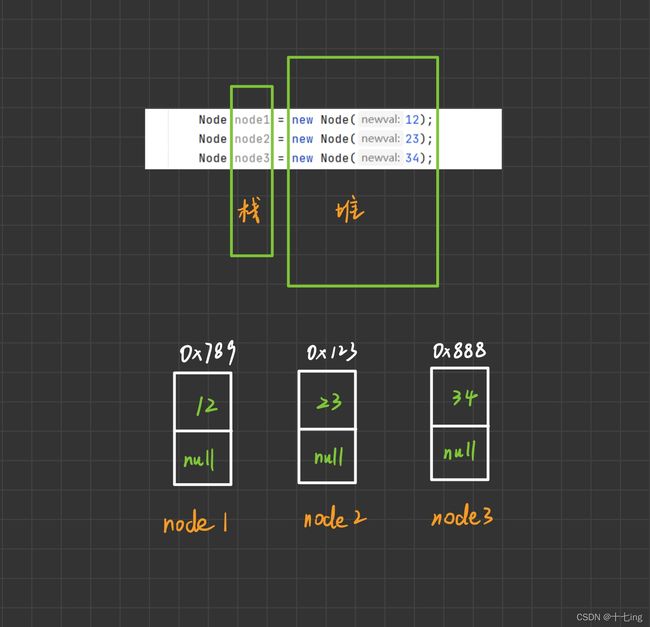
模拟五个节点,每个节点有两个域:
一个是数据域,存放的是元素
另一个是指针域,存放的是当前节点的下一个节点的地址

二、代码实现
1. 第一个 java 文件放的是两个类
一个类实现节点 Node,另一个类实现链表 LinkedList
class Node{
public int val;
public Node next;
public Node (int newval){
this.val = newval;
}
}
public class LinkedList {
//头指针
public Node head;
//初始化链表 ✓
public void initialList(){
Node node1 = new Node(12);
Node node2 = new Node(23);
Node node3 = new Node(34);
Node node4 = new Node(45);
Node node5 = new Node(56);
this.head = node1;
node1.next = node2;
node2.next = node3;
node3.next = node4;
node4.next = node5;
//此时的node5.next默认就是null
}
//打印链表每个节点存的元素 ✓
public void print(){
Node cur = this.head;
while(cur != null){
System.out.print(cur.val + " ");
cur = cur.next;
}
System.out.println();
}
//得到链表的长度 ✓
public int size(){
Node cur = this.head;
int count = 0;
while(cur != null){
count++;
cur = cur.next;
}
return count;
}
//头插法 ✓
public void addFirst(int data){
Node newnode = new Node(data);
if(this.head == null){
this.head = newnode;
return;
}
newnode.next = this.head;
this.head = newnode;
}
//尾插法 ✓
public void addLast(int data){
Node newnode = new Node(data);
if(this.head == null){
this.head = newnode;
return;
}
Node cur = this.head;
while(cur.next != null){
cur = cur.next;
}
cur.next = newnode;
}
//寻找要插入的位置,返回插入节点的前驱 ✓
public Node searchPos(int pos){
int sign = 0;
Node cur = this.head;
while(sign + 1 != pos){
sign++;
cur = cur.next;
}
return cur;
}
//任意位置插入,假设第一个数据节点为 0 号下标 ✓
public void insertData(int pos,int data){
//1. 位置不合法
if(pos<0 || pos>size()){
System.out.println("链表的插入位置不合法!");
}
//2. 头插
else if(pos == 0){
addFirst(data);
}
//3. 尾插
else if(pos == size()){
addLast(data);
}
//4. 中间插
else{
Node newnode = new Node(data);
Node cur = searchPos(pos);
newnode.next = cur.next;
cur.next = newnode;
}
}
//查找是否包含关键字key是否在单链表当中 ✓
public boolean contains(int key){
Node cur = this.head;
while(cur != null){
if(cur.val == key){
return true;
}else{
cur = cur.next;
}
}
return false;
}
//删除第一次出现关键字为key的节点 ✓
public void remove(int key){
//1. 链表为空
if(this.head == null){
System.out.println("链表为空,无法删除!");
return;
}
//2. 头删
if(this.head.val == key){
this.head = this.head.next;
return;
}
//3. 中间删 + 尾删
Node prev = this.head;
Node del = this.head;
while(prev.next != null){
if(prev.next.val != key){
prev = prev.next;
}
else{
del = prev;
del.next = del.next.next;
return;
}
}
System.out.println("你所删除的节点在链表中没有找到!");
}
//删除所有值为key的节点 ✓
public void removeAllKey(int key){
//1. 链表为空
if(this.head == null){
System.out.println("链表为空,无法删除!");
return;
}
//2. 开始删除重复的节点
Node cur = this.head;
Node prev = this.head;
while(cur != null){
if(cur.val == key){
prev.next = cur.next;
cur = cur.next;
}
else{
prev = cur;
cur = cur.next;
}
}
//3. 考虑头节点
if(this.head.val == key){
this.head = this.head.next;
}
}
//清空链表 ✓
public void clear(){
this.head = null;
}
}
2. 第二个 java 文件放的是一个类 Test
目的是使用主函数来测试单链表的一系列功能
public class Test {
public static void main(String[] args) {
LinkedList test = new LinkedList();
test.initialList();
test.print();
}
}
三、框架分析
0. 对框架进行说明
(1)我所创建的框架是拆解了代码的方法(函数),把类中的每一个方法都拿出来仔细分析。
(2)我画图的地方可能有些不规范,比如地址的表示形式,比如箭头指向等等,我旨在表达逻辑,所以请读者自行理解,也请大佬多多指点。
1. 创建一个类 Node,表示节点
class Node {
public int val;
public Node next;
}
创建一个类 Node,表示节点,每次插入一个节点,就使用这个类
每个节点有两个元素:
一个存的是当前节点的值 val
另一个存的是下一个节点的地址 next,next 的类型是引用,即当前的 Node.

2. 模拟链表内部结构
class Node {
public int val;
public Node next;
public Node(int newval){
this.val = newval;
}
}
public class LinkedList {
public static void main(String[] args) {
Node node1 = new Node(12);
Node node2 = new Node(23);
Node node3 = new Node(34);
}
}
说明:类 Node 中的 public Node(int newval) { },这是构造方法,以便于 LinkedList 中实例化对象,并赋值。
为了展现出清晰的链表结构,我们创建一个新的类 LinkedList,表示整个链表里面的结构,并在这个类中实现各种接口。我们尝试着直接往里面一个一个放数据,为了展示底层原理,我先放在主函数中以帮助理解。
我们为什么不把引用类型 next 置成 null 呢?因为 next 是一个成员变量,如果不将其初始化,那么默认为 null,即不指向任何对象的地址,下图辅助理解。
3. 初始化一个链表
public class LinkedList {
//头指针
public Node head;
//初始化链表 ✓
public void initialList(){
Node node1 = new Node(12);
Node node2 = new Node(23);
Node node3 = new Node(34);
Node node4 = new Node(45);
Node node5 = new Node(56);
this.head = node1;
node1.next = node2;
node2.next = node3;
node3.next = node4;
node4.next = node5;
//此时的node5.next默认就是null
}
}
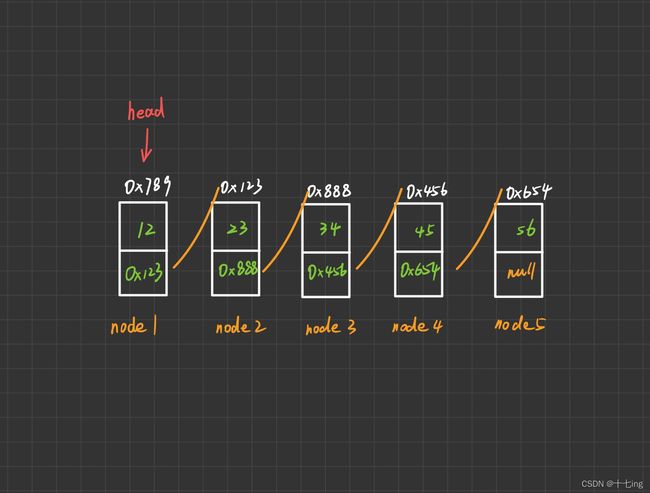
在上述的解释后,我们已经清楚地了解了关于链表的一些基础结构。
那么接下来,在类 LinkedList 中,创建一个方法 initialList,来初始化一个链表,并利用实例化后的对象来将各个节点串起来,并注意,我们要引用一个成员变量 head,以此来记住链表是从哪开始的!而链表的尾部我们不关心,因为它肯定是 null.
从目前来看,这是一个很笨的穷举方法,然而,我们的目的是深入理解链表。
4. 打印每个节点对应的 val
//打印链表每个节点 ✓
public void print(){
Node cur = this.head;
while(cur != null){
System.out.print(cur.val + " ");
cur = cur.next;
}
System.out.println();
}
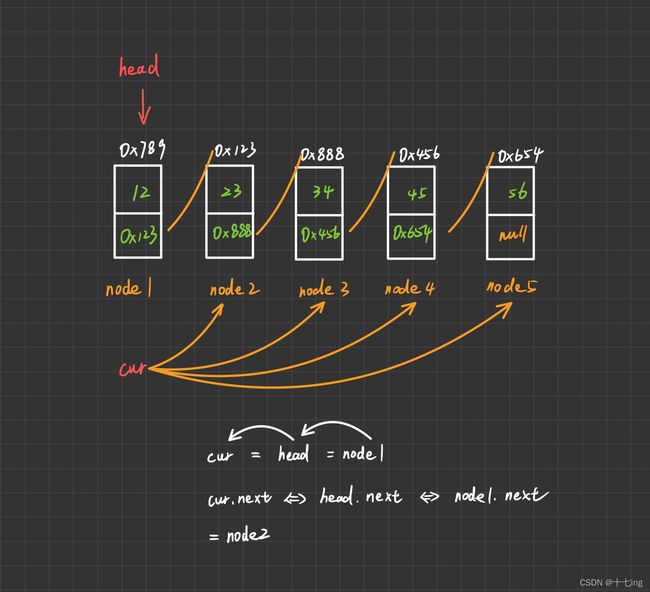
我们的思想是:遍历链表,当引用指向 null 时,那么就到了最后一个节点。
当然,我们要十分注意,要创建一个新的引用类型 cur,让这个 cur 去跑。因为你如果让 head 去遍历,head 不再指向第一个节点了,以此带来的结果是:我们不再能够控制链表,它就像一个无头苍蝇一样。
此外,我们让代码 cur = cur.next,来不断地拿到下一个节点的地址,以此来遍历,这和 C语言中的指针相似,只是实现方法不同。
下图辅助理解
5. 得到链表的长度
//得到链表的长度 ✓
public int size(){
Node cur = this.head;
int count = 0;
while(cur != null){
count++;
cur = cur.next;
}
return count;
}
6. 头插法
//头插法 ✓
public void addFirst(int data){
Node newnode = new Node(data);
if(this.head == null){
this.head = newnode;
return;
}
newnode.next = this.head;
this.head = newnode;
}
头插法的最关键的思想就是,改变头指针 head 指向的地址。
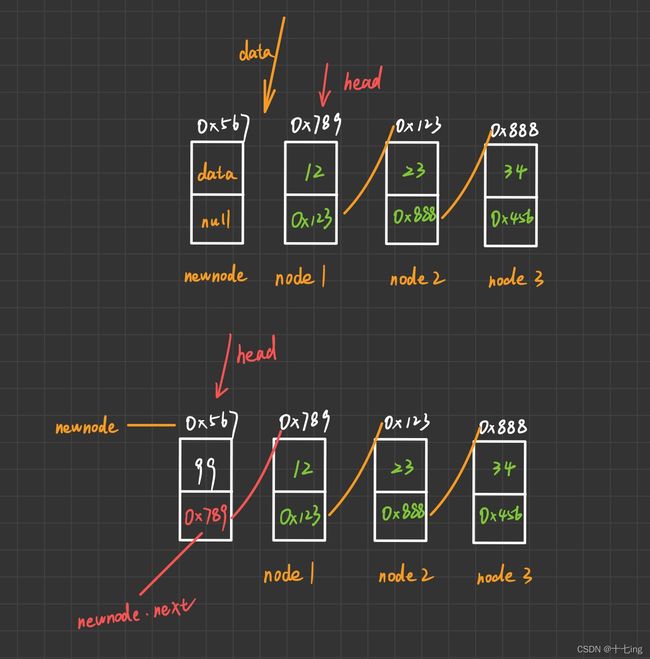
在没有插入数据之前,head 指向原先的 node1,在插入之后,新的节点 newnode 存放两个数据,一个是整型的 data,一个是空指针 null。
而我们要做的就是让 head 指向 newnode,而 newnode 这个新的节点存放的又是原先的 node1,所以我们通过以下两行代码进行实现
newnode.next = this.head <=> node1;
this.head = newnode;
而这两行核心代码不能颠倒顺序,否则,会导致死循环。
下图为辅助理解,应当注意的是,整个过程全部都是由地址实现转换的,另外,也要把整个链表为空的情况考虑进去。
7. 尾插法
//尾插法 ✓
public void addLast(int data){
Node newnode = new Node(data);
if(this.head == null){
this.head = newnode;
return;
}
Node cur = this.head;
while(cur.next != null){
cur = cur.next;
}
cur.next = newnode;
}
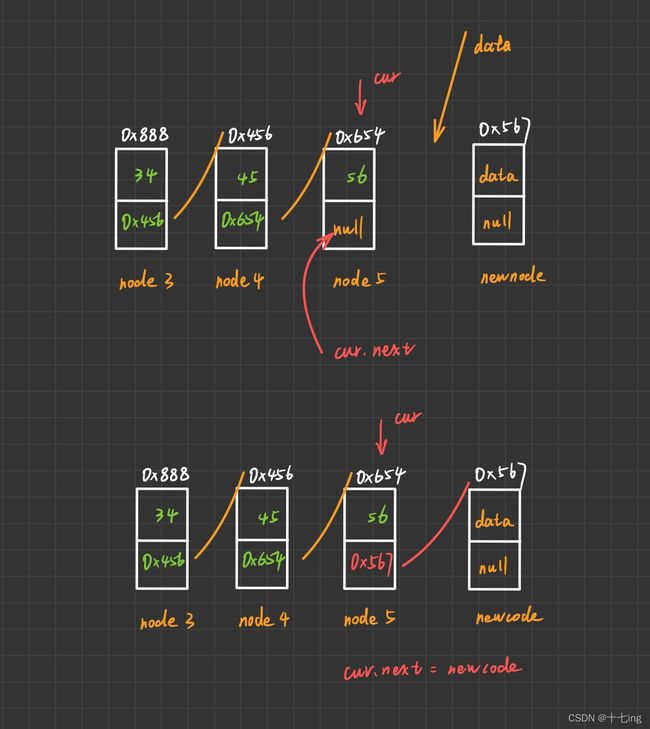
如果链表中有元素,那么就遍历链表找到最后一个节点存的地址,也就是 cur.next 必定为 null,然后就把新的节点地址赋给 cur.next。
下图为辅助理解,应当注意的是,整个过程全部都是由地址实现转换的,另外,也要把整个链表为空的情况考虑进去。
尾插法相比于头插法,较为简单,但是实现的思想相同。
8. 在任一位置插入节点
//寻找要插入的位置,返回插入节点的前驱 ✓
public Node searchPos(int pos){
int sign = 0;
Node cur = this.head;
while(sign + 1 != pos){
sign++;
cur = cur.next;
}
return cur;
}
//任意位置插入,第一个数据节点为0号下标 ✓
public void insertData(int pos,int data){
//1. 位置不合法
if(pos<0 || pos>size()){
System.out.println("链表的插入位置不合法!");
}
//2. 头插
else if(pos == 0){
addFirst(data);
}
//3. 尾插
else if(pos == size()){
addLast(data);
}
//4. 中间插
else{
Node newnode = new Node(data);
Node cur = searchPos(pos);
newnode.next = cur.next;
cur.next = newnode;
}
}
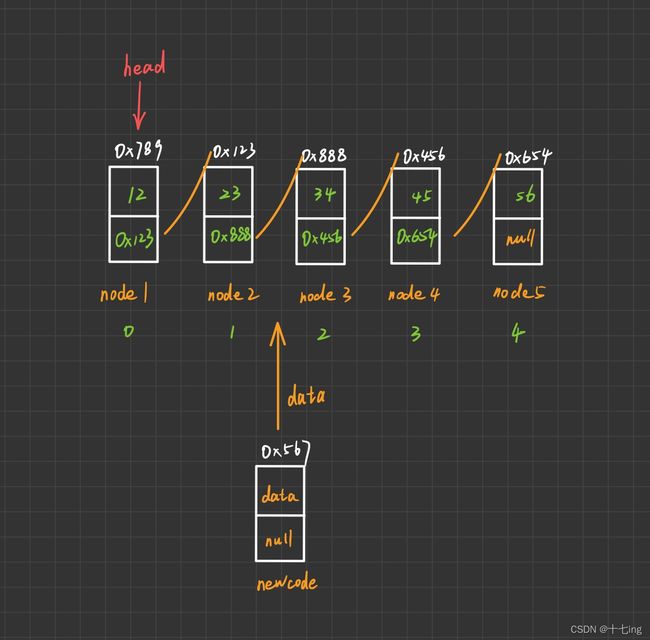
在中间位置插入数据之前,每个节点的 “内存” 是连着的,所以我们考虑插入数据之后,也要满足上面的要求,就像一根线把零散的珠子串起来一样,上述代码分为几种情况,读者可自行体会,而我们下面只分析中间插入节点的情况。
思路如下:
在类中创建两个方法
一个函数是 searchPos,用来找到要插入节点位置下标的,并返回节点的前驱 cur,因为前驱即将存的是我们插入节点的地址,我们假设把第一个节点的下标设置成 0,第二个节点的下标设置成 1…
另一个函数是 insertData,用来执行插入节点后的地址转换
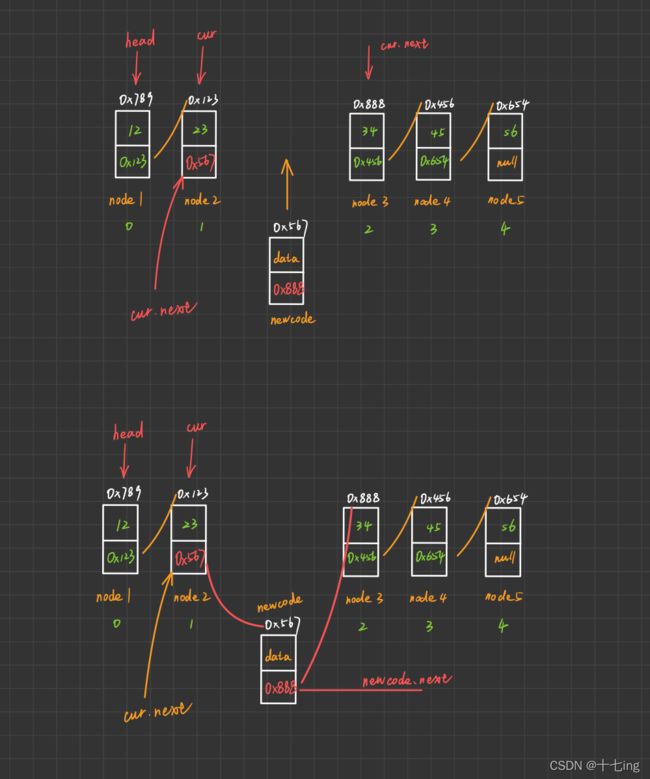
举个例子,我们在链表中插入的位置是下标 2,那么我们通过下面的图和代码进行演示,
而这两行核心代码不能颠倒顺序,否则,会导致死循环。
newcode.next = cur.next;
cur.next = newcode;
9. 查找关键字key是否在单链表当中
//查找是否包含关键字key是否在单链表当中 ✓
public boolean contains(int key){
Node cur = this.head;
while(cur != null){
if(cur.val == key){
return true;
}else{
cur = cur.next;
}
}
return false;
}
10. 删除第一次出现关键字为 key 的节点
//删除第一次出现关键字为key的节点 ✓
public void remove(int key){
//1. 链表为空
if(this.head == null){
System.out.println("链表为空,无法删除!");
return;
}
//2. 头删
if(this.head.val == key){
this.head = this.head.next;
return;
}
//3. 中间删 + 尾删
Node prev = this.head;
Node del = this.head;
while(prev.next != null){
if(prev.next.val != key){
prev = prev.next;
}
else{
del = prev;
del.next = del.next.next;
return;
}
}
System.out.println("你所删除的节点在链表中没有找到!");
}
这里就不再画图描述,思想和任意位置插入是一样的,所以我主要阐明一下步骤:
删除节点有如下几种情况:
(1)删除的链表是否为空
(2)如果链表不为空,删除的节点是否有对应的元素
(3)头删
(4)尾删
(5)中间删
假设我们删除的是 key 为 34,也就是 2 号位,那么我们一定要让 cur 走到 1号位,因为 1 号位是 2 号位的前驱,即1 号位存放着 2 号位的地址,然后通过如下代码,就可以完成目的,而删除尾部的节点,和此时的思想是一样的。
cur.next = cur.next.next
11. 删除所有出现 key 的节点
//删除所有出现 key 的节点 ✓
public void removeAllKey(int key){
//1. 链表为空
if(this.head == null){
System.out.println("链表为空,无法删除!");
return;
}
//2. 开始删除重复的节点
Node cur = this.head;
Node prev = this.head;
while(cur != null){
if(cur.val == key){
prev.next = cur.next;
cur = cur.next;
}
else{
prev = cur;
cur = cur.next;
}
}
//3. 考虑第一个节点
if(this.head.val == key){
this.head = this.head.next;
}
}
方法一:我们可以不断调用 remove 函数,一次调用删一个值,遍历很多次,然而这样的效率太低,所以我们可以尝试方法二。
方法二:我们可以只经过一次遍历,就可以达到所有删除的目的,下面我主要讲解方法二,方法二有两种情况。
(情况1)指定的节点在链表中非连续存放
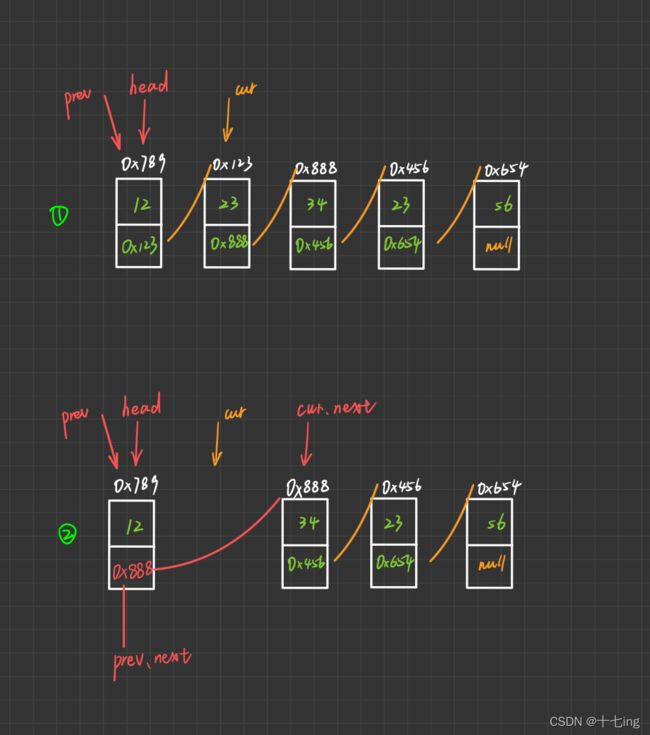
举个例子:假设我们要删除的节点对应值 key 为 23
那么下图开始我的分析
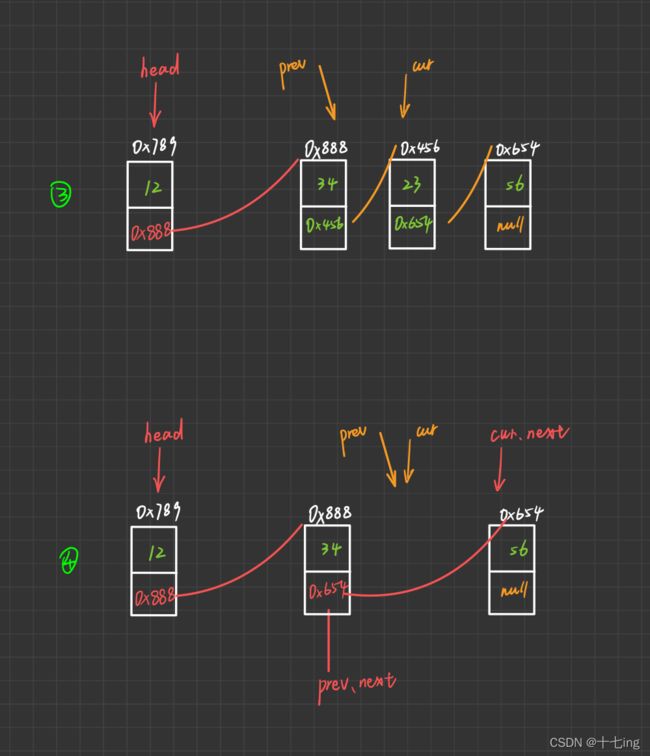

拆解步骤:
步骤①:我们创建两个引用(指针)
一个是 cur, 代表搜寻指针,指向 head.next,目的是让 cur 遍历整个链表,遇到对应的 key,那么就停下,没遇到对应的 key,就继续跑,直到遇到 null,就跳出循环。
另一个是 prev, 代表 cur 的前驱指针,指向 head,目的是跟随指针 cur,起到串联链表中零散节点的作用。
后面的步骤开始执行:
例如步骤②,如果遇到了 key ,就执行如下代码
prev.next = cur.next; //串联零散节点
cur = cur.next; //继续遍历
例如步骤③,如果没遇到 key ,就执行如下代码
prev = cur; //重置前驱
cur = cur.next; //继续遍历
最后判断第一个节点 head.val 是否 == key,是 key 就重新指向,读者可以思考,如果 head 放在程序最开始判断,那么 head 将不断被改变,因为我们要删除 key 对应的节点的位置是不可预知的,这样考虑下来,直接将头指针放置在程序最后判断较为方便。
而最后一个节点是否有对应的 key 我们不用关心,因为它仍然符合以上代码。
此外,还有一种情况:
(情况2)指定的节点在链表中连续存放
此情况被被情况(1)包含,所以仍然符合以上代码,读者可以自行画图分析。
12. 清空链表
//清空链表 ✓
public void clear(){
this.head = null;
}
四、测试程序
1. 初始化链表
public class Test {
public static void main(String[] args) {
LinkedList test = new LinkedList();
test.initialList();
test.print();
}
}
2. 插入功能
public class Test {
public static void main(String[] args) {
LinkedList test = new LinkedList();
test.addFirst(1);
test.addFirst(3);
test.addFirst(5);
test.addFirst(7);
test.print();
test.addLast(2);
test.addLast(4);
test.addLast(6);
test.addLast(8);
test.print();
test.insertData(8,77);
test.print();
test.insertData(0,99);
test.print();
test.insertData(2,88);
test.print();
}
}
3. 删除单节点
public class Test {
public static void main(String[] args) {
LinkedList test = new LinkedList();
test.addLast(1);
test.addLast(3);
test.addLast(5);
test.addLast(7);
test.addLast(9);
test.print();
test.remove(9);
test.print();
test.remove(1);
test.print();
test.remove(5);
test.print();
test.remove(10);
}
}
4. 删除指定的重复节点
public class Test {
public static void main(String[] args) {
LinkedList test = new LinkedList();
test.addLast(2);
test.addLast(3);
test.addLast(5);
test.addLast(2);
test.addLast(2);
test.addLast(9);
test.addLast(2);
test.print();
test.removeAllKey(2);
test.print();
}
}
总结
- 刚接触单链表的时候,花了我很长时间,可能我和大家不一样,底层思想我是很快就懂了,但是使用 Java 代码实现的时候,却花了我很长时间。
- 总体来说,Java 实现链表确实要简洁一点,C / C++ 实现我没用过,但是肯定少不了指针和结构体,因为目前刚刚接触到类与对象的概念,从面向过程到面向对象,这是一个思维的大改变,确实不容易,使用引用的时候,很不习惯。
- 现在慢慢接触数据结构,还是很吃力的,我发现画图也是很重要的,如果草图表达的清楚了,并且自己可以耐心地一步步往下推,那么剩下的就是语法实现而已。