牛客网面试必刷TOP101之——反转与合并链表

⚓️作者简介：即将大四的北京某能源高校学生。
 
座右铭：“九层之台，起于垒土” 。所以学习技术须脚踏实地。
 
这里推荐一款刷题、模拟面试神器，可助你斩获大厂offer：点我免费刷题、模拟面试

前言

牛客网是一个集笔面试系统、题库、课程教育、社群交流、招聘内推于一体的招聘类网站，更是一个专注于程序员的学习和成长的平台。
 
在某次浏览博客的过程中，我偶然点进一个链接，注册了牛客账号。一来到牛客首页，我就被其丰富的功能与良好的社区环境所吸引：

进入题库，更是有最新校招试题与专项练习：
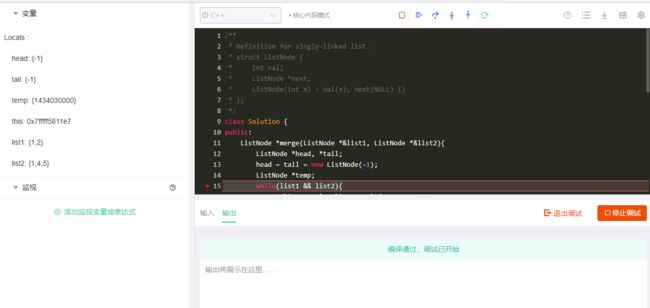
在线编程更是有在线调试功能，可大大提高debug效率：

问答题下还有超多牛客用户交流：

总之，牛客是一个专注于程序员的学习和成长的平台，所以我极力推荐大家注册牛客，坚持刷题，充实自己，大厂offer便指日可待。

链表基础题

 链表，别名链式存储结构或单链表，用于存储逻辑关系为 “一对一” 的数据。与顺序表不同，链表不限制数据的物理存储状态，换句话说，使用链表存储的数据元素，其物理存储位置是随机的。

下面来刷几个链表题练练手

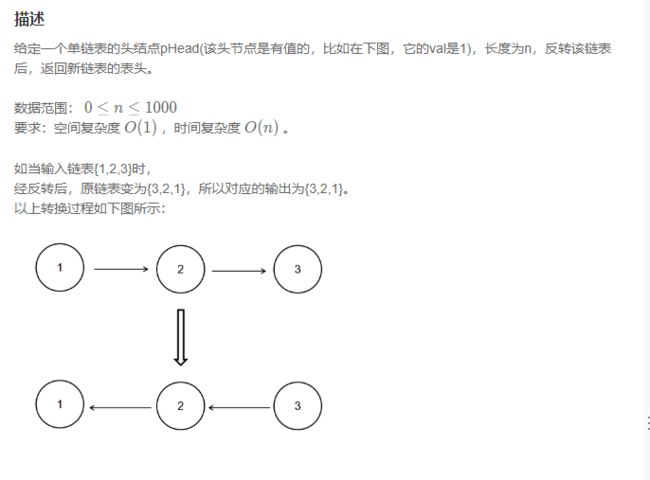
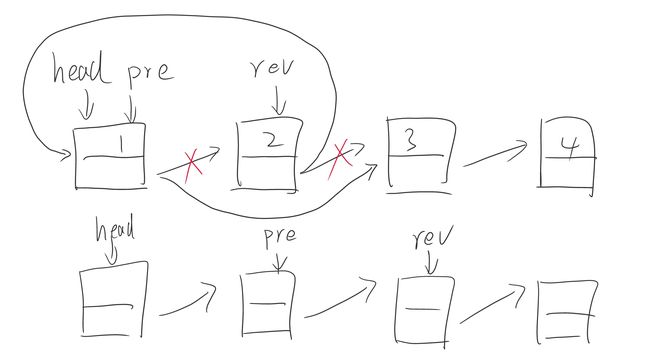
1.反转链表

题目：
示例：

解题思路

本题为题简单，思路也比较清晰：

维护三个指针：

• pre：指向要翻转结点的前一个结点，用来跳过要翻转的结点；
• rev：指向要翻转结点，用来将其指向头结点；
• head：指向整个翻转过程的头结点。

翻转过程：

• 将pre指向rev的下一个结点；
• rev的下一个结点指向head；
• head指向rev；
• rev指向pre的下一个结点。

图解示例：

C++解题代码：

class Solution {
public:
    ListNode* ReverseList(ListNode* pHead) {
        if(!pHead || !(pHead->next)) return pHead;
        ListNode* pre = pHead, *rev = pHead->next;
        while(rev != NULL){
            pre->next = rev->next;
            rev->next = pHead;
            pHead = rev;
            rev = pre->next;
        }
        return pHead;
    }
};

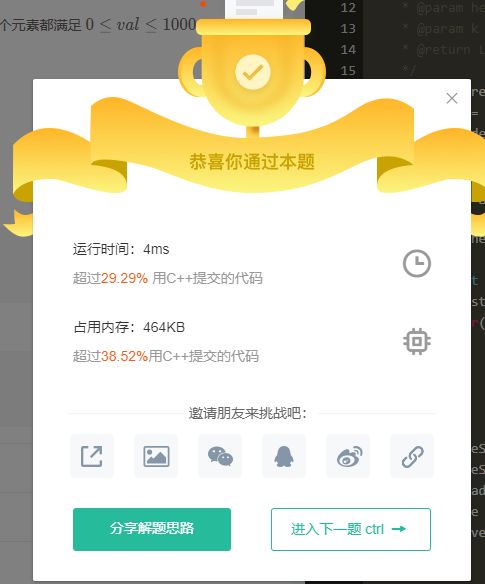
这道题还是比较基础的，但我的解法并不是最优的，运行时间还比较慢，大家要是想了解这道题的更优解法可以点击链接去学习哦。
此外有一点：牛客提交的运行时间并不是固定的，同一个答案提交几次运行时间和内存消耗是不一样的，大家要注意这点。

2.链表内指定区间反转

题目：

示例：

解题思路

找到第 m 个结点的前驱，与第 m 个结点，结合上一题的代码进行翻转即可

C++解题代码：

class Solution {
public:
    /**
     * 
     * @param head ListNode类 
     * @param m int整型 
     * @param n int整型 
     * @return ListNode类
     */
    ListNode* reverseBetween(ListNode* head, int m, int n) {
        int i = 1;
        ListNode *pHead = head, *Pre = pHead;
        for(;i < m;++i) {Pre = pHead;pHead = pHead->next;}
        if(!pHead || !(pHead->next)) return head;
        ListNode* pre = pHead, *rev = pHead->next;
        while(i < n){
            pre->next = rev->next;
            rev->next = pHead;
            pHead = rev;
            rev = pre->next;
            if(m!=1)
                Pre->next = pHead;
            ++i;
        }
        return (m==1)?pHead:head;
    }
};

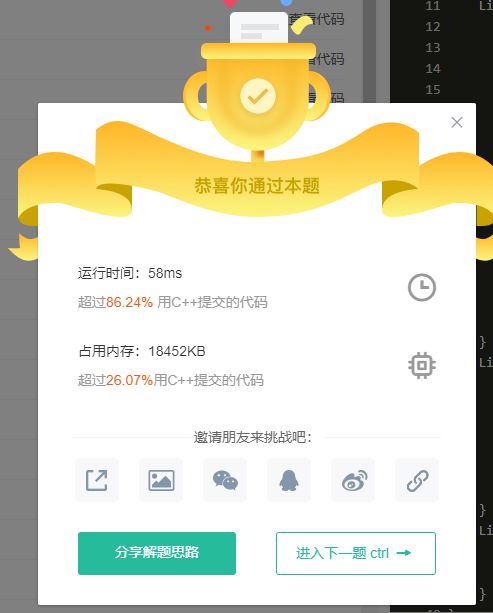
本题也属于简单题，理解上一题的原理这题就不难做出来，但是要注意对 m 等于 1 的情况特殊处理，这就是不带头节点的链表的缺点。牛客题解中有添加头结点的方法，大家可以参考。

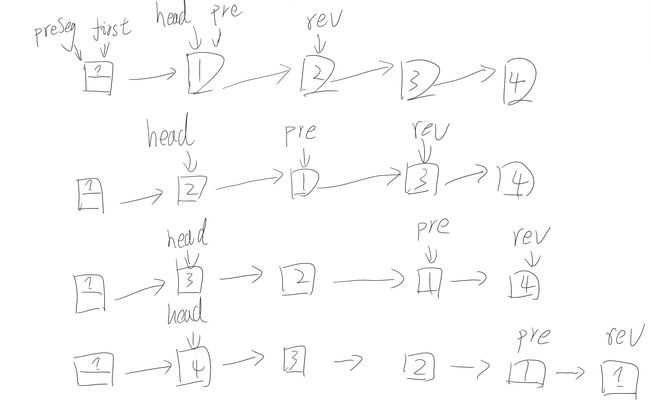
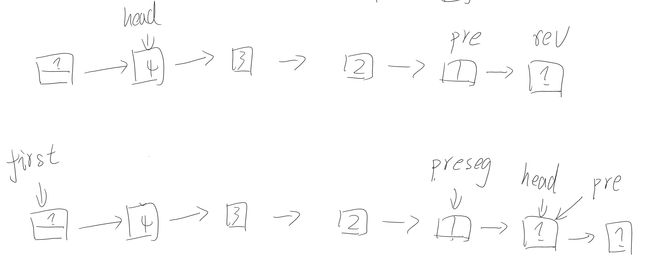
3. 链表中的节点每k个一组翻转

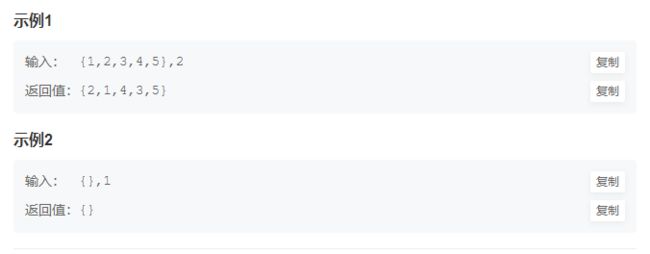
题目：

示例：

解题思路：
将链表划分为 链表长度/k 个小链表，在小链表内部进行翻转，同时应该注意小链表之间的连接问题。

图解示例一：

链表内部翻转，添加头结点，翻转过程与第一题翻转整个链表一样。多了两个指针，功能如下：

• first 用来指向头结点；
• preseg 用来指向小链表的头结点；

图解示例二：
连接小链表。

C++解题代码

class Solution {
public:
    /**
     * 
     * @param head ListNode类 
     * @param k int整型 
     * @return ListNode类
     */
    ListNode* reverseKGroup(ListNode* head, int k) {
        if(k == 1 || head == nullptr) return head;
        ListNode *first = new ListNode(-1);
        first->next = head;
        ListNode *preSeg = first, *pre = head;
        int length = 0;
        while(pre){pre = pre->next;++length;}
        pre = head;
        
        for(int i = 0; i < length/k;++i){
            ListNode *reverse = head->next;
            for(int j = 1; j < k; ++j){
                pre->next = reverse->next;
                reverse->next = head;
                head = reverse;
                reverse = pre->next;
            }
            preSeg->next = head;
            preSeg = pre;
            head = reverse;
            pre = reverse;
            reverse = reverse->next;
        }
        
        return first->next;
    }
};

本题还是前两题的拓展，处理好小链表的连接问题就很容易解决了。

4.合并k个已排序的链表

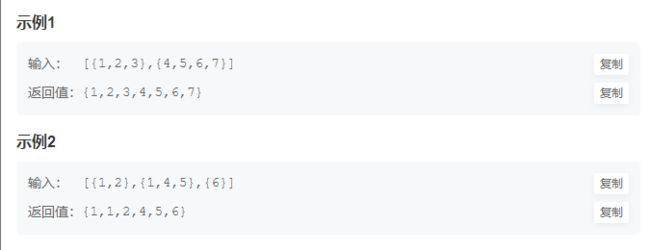
题目：

示例：

解题思路：
思路一：将所有链表的第一个节点数据存入一个大小为 k 的数组，每次遍历找到最小的，然后这个链表第二个节点进入数组替代该值。但时间复杂度为$O(n^2)$，不满足题意。

思路二：将所有链表的所有值存入一个向量，排序后再构造链表，时间复杂度$O(nlogn)$，但空间复杂度变大了，需要一个临时向量和新链表，时间复杂度为$O(n)$。

思路三：像归并排序的归并步骤一样将链表归并起来：

归并的过程需要维护一个链表来存储归并后的元素，空间复杂度为$O(n)$，而时间复杂度则为$O(nlogn)$。

C++解题代码

class Solution {
public:
    ListNode *merge(ListNode *&list1, ListNode *&list2){
        ListNode *head, *tail;
        head = tail = new ListNode(-1);
        while(list1 && list2){
            if(list1->val < list2->val){
                tail->next = list1;
                list1 = list1->next;
            }else{
                tail->next = list2;
                list2 = list2->next;
            }
            tail = tail->next;
        }
        if(!list1) tail->next = list2;
        if(!list2) tail->next = list1;
        return head->next;
    }
    ListNode *merge(vector<ListNode *> &lists, size_t lo, size_t hi){
        if(lo == hi) return lists[lo];
        size_t mid = lo + (hi - lo)/2;
        ListNode *list1 = merge(lists, lo, mid);
        ListNode *list2 = merge(lists, mid + 1, hi);
        return merge(list1, list2);
    }
    ListNode *mergeKLists(vector<ListNode *> &lists) {
        if(!lists.size()) return nullptr;
        return merge(lists, 0, lists.size() - 1);
    }
};

本题主要考察的点是把时间复杂度控制在$O(nlogn)$内，而利用归并正好可以做到这点。

我希望通过写博客来结束浑浑噩噩的生活，我更希望通过刷题结束人云亦云的思考。朋友们，刷题不仅仅是刷题，还是我们与自己内心深处的对话。希望我们可以一起在牛客刷题交流，一起收割大厂offer