GNN(图神经网络)在反欺诈领域的落地
今天的博客主要参考了《Heterogeneous Graph Neural Networks for Malicious Account Detection》和《GeniePath: Graph Neural Networks with Adaptive Receptive Paths》,都来自阿里的蚂蚁金服团队,都使用了当下最流行的Graph Neural Network的相关知识。
其实有关GCN的相关基础知识在网上都查的到,特别是后面涉及到的数学知识还是十分复杂的,这里就不详细推导每一个步骤了。这里就给出一个最终的结论,也是Kipf and Welling在2016年GCN领域最经典的paper《Semi-supervised classification with graph convolutional net- works.》里对原始的基于拉普拉斯谱变换进行了一些简化得到最终的图卷积公式如下:
H ( t + 1 ) = σ ( A u H ( t ) W ( t ) ) H^{(t+1)}=\sigma (A^{u} H^{(t)}W^{(t)}) H(t+1)=σ(AuH(t)W(t)),其中 A u A^u Au是一个对称归一化矩阵, A u = D ∗ − 1 / 2 A ∗ D ∗ − 1 / 2 A^u=D^{*-1/2}A^*D^{*-1/2} Au=D∗−1/2A∗D∗−1/2, A ∗ = A + I A^*=A+I A∗=A+I,其中 I I I是单位矩阵, A A A是临接矩阵, D ∗ D^* D∗是矩阵 A ∗ A^* A∗的对角度矩阵, H ( t ) ∈ R N , K H^{(t)} \in R^{N,K} H(t)∈RN,K是第t层的中间隐层表示。 H ( 0 ) = X H^{(0)}=X H(0)=X,即初始的输入是每一个node节点的embedding表示,这样最后GCN输出的最后一层节点的Embedding包不但包含了节点的初始特征还包含了网络的拓扑特征。从GCN最基本的变换公式可以看出,我们需要做的是结合业务场景定义的是临接矩阵 A u A^u Au和节点的初始状态 H ( 0 ) = X H^{(0)}=X H(0)=X。
上面其实是最基本的GCN的函数形式,以后所有的GCN变体都是在这个基础之上进行衍生,比方说当 A u = D ∗ − 1 A ∗ A^u=D^{*-1}A^* Au=D∗−1A∗的时候,就是另一种形式的GCN。
介绍完了GCN的一些基础知识,下面开始正式讲解paper。
首先讲的paper是《Heterogeneous Graph Neural Networks for Malicious Account Detection》,即在异构网络中使用Graph Neural network去进行欺诈。首先作者根据分析出的欺诈账户规律,总结出了黑产用户活动的2个规律:1 Device aggregation(设备聚集性,这里的设备是一个 抽象的概念,具体化可以有IP,设备ID,账户等信息。设备聚集性说的是黑产手中的设备资源是有限的); 2 Activity aggregation(活动方式的聚集性,即由于黑产设备是在同一批的控制之下活动的,那么这些账户之间一定存在着较大的共线性)。理解这两个黑产活动规律是很重要的,后面的模型都是针对这两个规律构建的。
正如paper标题中所说的,论文提出的是一个异构网络,即网络中的节点包括了2类:Account(账户) 和 Device(设备资源)。如果网络中某一个节点account i在设备节点device j上有登录或者注册等行为(这里的account可以认为是主维度字段,device可以认为是关联维度字段),那么节点i和j之间就有一条边(个人认为这样的定义有点太宽松了,应该加上时间窗口),这样N个account和device的节点就可以形成一个网络 G G G,其临接矩阵的表征形式为 A G ∈ { 0 , 1 } N , N A ^G\in \{0,1\}^{N,N} AG∈{0,1}N,N。由于这里面的设备是一个抽象的概念,如果具体的话可以有IP,设备ID,阿里设备指纹等形式(假设具体的设备字段个数为D),所有针对某一类具体的设备字段 d d d会有一个sub-graph即 G d G^d Gd,而 G d G^d Gd的邻居矩阵维度即顶点数和 G G G一样,只不过只留下了和当前type d有关系的边。
接下来我们要定义节点的初始状态矩阵 X ∈ R N , p + ∣ D ∣ X\in R^{N,p+|D|} X∈RN,p+∣D∣,这里可以发现矩阵的行数是节点的数量N,而列数是 p + ∣ D ∣ p+|D| p+∣D∣。其中p是当节点为account时,将数据按照时间划分出 p p p个time slot(在实际工程中,可以加入其它和节点相关的特征进去),并统计每一个time slot中的操作次数;而 D D D则是当节点为device不同关联维度的种类数即type d的数量,这里采用的是one-hot编码的方式。由于是异构网络,即一个矩阵中存在含义不同的节点,但是为了保证每一个节点的维度都一致,多余的维度即针对account 节点来说就多余了 D D D为,对于device 节点来说就多余了 p p p维,都采用填充0的方式进行对齐。下面就是图神经网络的递推迭代公式:
H ( 0 ) = 0 ( 矩 阵 ) H^{(0)}=0(矩阵) H(0)=0(矩阵) 公式一
H ( t ) = σ ( X W + 1 ∣ D ∣ ∑ d = 1 ∣ D ∣ A ( d ) H ( t − 1 ) V d ) H^{(t)}=\sigma (XW+\frac{1}{|D|}\sum_{d=1}^{|D|}A^{(d)}H^{(t-1)}V_d) H(t)=σ(XW+∣D∣1∑d=1∣D∣A(d)H(t−1)Vd) 公式二
其中 H ( t ) ∈ R N , k H^{(t)}\in R^{N,k} H(t)∈RN,k属于图神经网络的中间层输出, W ∈ R ( p + ∣ D ∣ ) ∗ k W \in R^{(p+|D|)*k} W∈R(p+∣D∣)∗k和 V d ∈ R k ∗ k V_d \in R^{k*k} Vd∈Rk∗k属于模型参数,随着模型一起学习。最后的损失函数,即当T层之后,可以使用少部分标注数据进行网络参数的学习,最终的损失函数是交叉熵形式为: L = − ∑ i N 0 l o g σ ( y i , ( u T , h T ) ) L=-\sum_{i}^{N_0}log \sigma(y_i,(u^T,h_T)) L=−∑iN0logσ(yi,(uT,hT))。
这里作者发现,在公式一中,可以使用attention机制来优化效果,即优化升级公式二引入attention机制,得到
H ( t ) = σ ( X W + 1 ∣ D ∣ ∑ d ∈ D s o f t m a x ( α d ) A ( d ) H ( t − 1 ) V d ) H^{(t)}=\sigma (XW+\frac{1}{|D|}\sum_{d \in D}softmax(\alpha_d)A^{(d)}H^{(t-1)}V_d) H(t)=σ(XW+∣D∣1∑d∈Dsoftmax(αd)A(d)H(t−1)Vd) 公式三
其中, s o f t m a x ( α d ) = e x p ( α d ) ∑ i e x p ( α i ) softmax(\alpha_d)=\frac{exp(\alpha_d)}{\sum_i exp(\alpha_i)} softmax(αd)=∑iexp(αi)exp(αd),其中 α = [ α 1 , α 2 , . . . . α ∣ D ∣ ] T ∈ R ∣ D ∣ \alpha=[\alpha_1,\alpha_2,....\alpha_{|D|}]^T \in R^{|D|} α=[α1,α2,....α∣D∣]T∈R∣D∣。
第二篇要讲的paper是《GeniePath: Graph Neural Networks with Adaptive Receptive Paths》,从题目中可以看到“Adaptive Receptive Paths”,即自适应的最佳搜索路径。
这也是本篇paper最大的创新点和贡献点,这个创新点是相对于基础的GCN来讲的,从上面可知基础的GCN迭代公式形式为: H ( t + 1 ) = σ ( A u H ( t ) W ( t ) ) H^{(t+1)}=\sigma (A^{u} H^{(t)}W^{(t)}) H(t+1)=σ(AuH(t)W(t)),如果神经网络的层数为T,那么T层的节点输出就是考虑了距离当前节点t距离为T的所有邻居,为了增加考虑的邻居数,可以不断的增加T,但是过多的层数会导致模型参数量过大,导致模型在训练的时候难以收敛,故有些paper会结合残差网络的概念引入残差网络,即 H ( t + 1 ) = F ( H ( t ) , A , X ) + H ( t ) H^{(t+1)}=F(H^{(t)},A,X)+H^{(t)} H(t+1)=F(H(t),A,X)+H(t)。
但是这样依然是会有2个比较显著的缺陷:1 并不是所有邻居都是同等重要的(对应paper里的breadth 方向的Adaptive Receptive Paths);2 并不是所有深度搜索的路径都是一样重要的(对应paper里的depth方向的Adaptive Receptive Paths)。
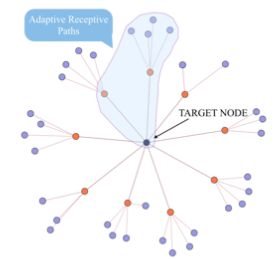
上图形象的说明了adaptive receptive path的概念,即目标target节点周围的邻居以及对应更远的hop的路径重要程度是不一样的,图中有浅蓝色底色的区域就是adaptive receptive path。至于哪些邻居节点以及哪些更远的延伸路径是adaptive receptive path,这就是本篇paper要解决的问题了。
基于此,paper提出了基于breadth 和depth两个方向自适应优化的算法框架:
for t = 1 t=1 t=1 to T T T
H ( t m p ) = ϕ ( A , H ( t − 1 ) ; θ ) H^{(tmp)}=\phi(A,H^{(t-1)};\theta) H(tmp)=ϕ(A,H(t−1);θ) breadth function
//这里需要注意的是, breadth function需要具备permutation invariant的性质,即无论邻居节点输入的顺序如何, breadth function生成的结果都是一样的
H ( t ) = η ( H ( t m p ) ∣ { H ( τ ) ∣ τ ∈ t − 1 , . . . . 0 } ) H^{(t)}=\eta(H^{(tmp)}|\{H^{(\tau)}|\tau \in {t-1,....0}\}) H(t)=η(H(tmp)∣{H(τ)∣τ∈t−1,....0}) depth function
具体来说:
breadth function 形式: h i ( t m p ) = t a n h ( W t ∑ j ∈ N ( i ) α ( h i t , h j t ) . h j t ) h_i^{(tmp)}=tanh(W^{t}\sum_{j\in N(i)}\alpha(h_i^t,h_j^t).h_j^t) hi(tmp)=tanh(Wt∑j∈N(i)α(hit,hjt).hjt),其中 α ( x , y ) = s o f t m a x ( V T t a n h ( W s T x + W d T y ) ) \alpha(x,y)=softmax(V^Ttanh(W_s^Tx+W_d^Ty)) α(x,y)=softmax(VTtanh(WsTx+WdTy))。
depth function 形式(很大程度上借鉴了LSTM的信息流控制形式):
i i = σ ( W i ( t ) h i ( t m p ) ) i_i=\sigma(W_i^{(t)}h_i^{(tmp)}) ii=σ(Wi(t)hi(tmp))
f i = σ ( W f ( t ) h i ( t m p ) ) f_i=\sigma(W_f^{(t)}h_i^{(tmp)}) fi=σ(Wf(t)hi(tmp))
o i = σ ( W o ( t ) h i ( t m p ) ) o_i=\sigma(W_o^{(t)}h_i^{(tmp)}) oi=σ(Wo(t)hi(tmp))
C ∗ = t a n h ( W c ( t ) h i ( t m p ) ) C^*=tanh(W_c^{(t)}h_i^{(tmp)}) C∗=tanh(Wc(t)hi(tmp))
C i ( t + 1 ) = f i ⨀ C i ( t ) + i i ⨀ C ∗ C_i^{(t+1)}=f_i\bigodot C_i^{(t)}+i_i\bigodot C^* Ci(t+1)=fi⨀Ci(t)+ii⨀C∗
h i ( t + 1 ) = o i ⨀ t a n h ( C i ( t + 1 ) ) h_i^{(t+1)}=o_i\bigodot tanh(C_i^{(t+1)}) hi(t+1)=oi⨀tanh(Ci(t+1))
对于每一个节点i来讲, C i 0 = 0 C_i^0=0 Ci0=0
这两个步骤的具体表现如下图所示:
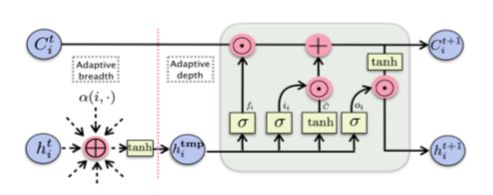
图中 ⨁ \bigoplus ⨁操作代表了 ∑ j ∈ N ( i ) α ( h i t , h j t ) . h j t ) \sum_{j\in N(i)}\alpha(h_i^t,h_j^t).h_j^t) ∑j∈N(i)α(hit,hjt).hjt)。
另一种综合考虑breadth function和depth function的变体Variant形式
即将depth function的操作推迟,首先仅仅按照breadth function操作对原始输入数据进行T层转换,得到每一层的输出结果向量 { h i 0 , h i 1 , . . . h i T } \{h_i^0,h_i^1,...h_i^T\} {hi0,hi1,...hiT},接下来将 h i h_i hi序列输入到下述变换公式中:
i i = σ ( W i t i_i=\sigma(W_i^t ii=σ(Wit c o n c a t ( h i t , μ i t ) ) concat(h_i^t,\mu_i^t)) concat(hit,μit))
f i = σ ( W f t f_i=\sigma(W_f^t fi=σ(Wft c o n c a t ( h i t , μ i t ) ) concat(h_i^t,\mu_i^t)) concat(hit,μit))
o i = σ ( W o t o_i=\sigma(W_o^t oi=σ(Wot c o n c a t ( h i t , μ i t ) ) concat(h_i^t,\mu_i^t)) concat(hit,μit))
C ∗ = t a n h ( W c t ) C^*=tanh(W_c^t) C∗=tanh(Wct) c o n c a t ( h i t , μ i t ) ) concat(h_i^t,\mu_i^t)) concat(hit,μit))
C i t + 1 = f i ⨀ C i t + i t ⨀ C ∗ C_i^{t+1}=f_i \bigodot C_i^t+i_t\bigodot C^* Cit+1=fi⨀Cit+it⨀C∗
μ i t + 1 = o i ⨀ t a n h ( C i t + 1 ) \mu_i^{t+1}=o_i \bigodot tanh(C_i^{t+1}) μit+1=oi⨀tanh(Cit+1)
其中 μ i 0 = W x T X i \mu_i^0=W_x^TX_i μi0=WxTXi
这两年GNN以及GCN的概念还是非常火的,个人经验是,我们在运用的时候,网络层间的迭代公式使用目前常用的几种就可以,作为算法工程师的我们唯一需要注意的地方就是:1 定义好临接矩阵 A A A的形式;2 定义好节点特征状态 X X X的初始形式。接下来就可以使用GCN来直接进行节点的分类,或者提取节点的全面特征,供后续的分类所用。