Japanese Student Championship 2021

考试情况

前四题用了20分钟全部A掉
就开始自闭的过程
做完以后看了眼排行榜，发现F题做出来的人其实比E题做出来的人还多
自己审了一遍题，对E题其实也没什么思路，就跳过，去搞F了，因此自闭了一个半小时，只打出来了一个暴力，其他就不会搞了

总结

自我感觉非常好，手速和脑速同时在线，最起码就前四题而言，对自己非常满意了
但还是缺乏解决难题的能力（还是我太菜了吧）

题解

E

可以考虑到一些性质，假设该字符串为k级回文串，那么将这个字符串拆成2个字符串，若这两个字符串仍回文，那它们就是k-1级回文串，直到拆分成1级回文串后，再拆分出的字符串就不能再回文，否则就会改变最终结果
例如第五组样例中
2
acaabcbababaaac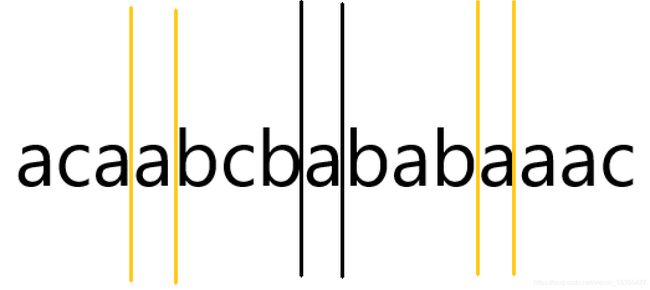
用黑线分隔开的两部分，应为回文串，并且这整个字符串也应为回文串
即要求acaabcb回文，babaaac回文，acaabcbababaaac回文
但用黄线分割开的部分不能回文
即要求aca不回文，bcb不回文，bab不回文，aac不回文
故可以发现第一个字符，第七个字符，第九个字符，第十五个字符必须相同，以此类推

符合上述条件的即为要求的二级回文串
可以提前进行一个处理，用二分的思想，将每个数找到它要与哪个数相等，用并查集将这个数视为它的祖先

这样的话，只需要找出每一组中出现次数最多的字符即可，然后可以算出一个初值，即将所有组用最优方式修改
但会出现特殊情况，即修改完以后，黄线分割开的部分有回文串，所以我们不光需要找到每一组出现最多的字符，还要找出出现次多的字符，当出现上述情况时，只需要修改一个字符就可以使最终的字符串符合题意，所以我们只需要求出修改哪个字符，使最后结果最优即可

code

#include
const int N=500005; 
using namespace std;
int k,n,p,v[N],fa[N],c[N][27],mx[N],q[N],id[N],ans;
char s[N];
void err()
{
	puts("impossible");
	exit(0);
}
int find(int k)
{
	if(k==fa[k]) return k;
	else return fa[k]=find(fa[k]);
}
void solve(int l,int r,int k)
{
	if(!k) return;
	int mid=l+r>>1;
	if((l+r)&1) solve(l,mid,k-1),solve(mid+1,r,k-1); 
	else solve(l,mid-1,k-1),solve(mid+1,r,k-1);
	for(int i=l;i<l+r-i;i++) fa[r+l-i]=i;
}
int main(){
	scanf("%d%s",&k,s+1);
	p=n=strlen(s+1);
	for(int i=1;i<=n;i++) fa[i]=i; 
	for(int i=1;i<=k;i++)
	{
		if(!p) err();
		p>>=1;
	}
	if(p==1) err();
	solve(1,n,k);
	for(int i=1;i<=n;i++) mx[i]=q[i]=-N,c[find(i)][s[i]-'a']++;
	for(int j=1;j<=n;j++)
		if(find(j)==j)
			for(int i=0;i<27;i++)
			{
				if(c[j][i]>mx[j]) q[j]=mx[j],id[j]=i,mx[j]=c[j][i];
				else if(c[j][i]>q[j]) q[j]=c[j][i];
			}
	for(int i=1;i<=n;i++) if(find(i)==i) ans+=mx[i];
	if(!p)
	{
		printf("%d",n-ans);
		return 0;
	}
	int fl=0,mn=N;
	for(int i=1;i<=p;i++) if(id[i]!=id[p-i+1]) fl=1;
	if(!fl)
	{
		for(int i=1;i<=p;i++) if(i+i-1!=p) mn=min(mn,mx[i]-q[i]);
		ans-=mn;
	}
	printf("%d",n-ans);
	return 0;
}