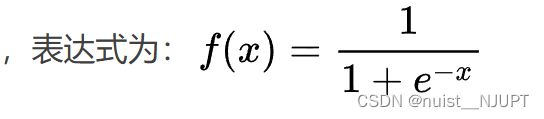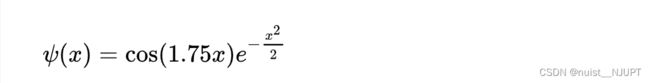备战数学建模46-小波神经网络WNN(攻坚站11)

我们之前学过BP神经网络，今天我们学习一下小波神经网络，和BP神经网络相比，小波神经网络拥有小波变换的优点，避免了 BP 网络设计结构上的盲目性，但是隐含层的节点数以及各层之间的权值、尺度因子的初始化参数难以确定，会影响网络的收敛速度。在后续的学习中，可以尝试其他小波函数的神经网络，通过比较其最优结果构造小波神经网络。

目录

一、小波神经网络案例

1.1、比较BP神经网络和小波神经网络

1.2、小波神经网络建立

 1.3、小波神经网络的预测流程图

1.4、数据集准备

 1.5、小波神经网络预测短时交通流MATLAB代码及结果分析

1.6、小结

---

一、小波神经网络案例

1.1、比较BP神经网络和小波神经网络

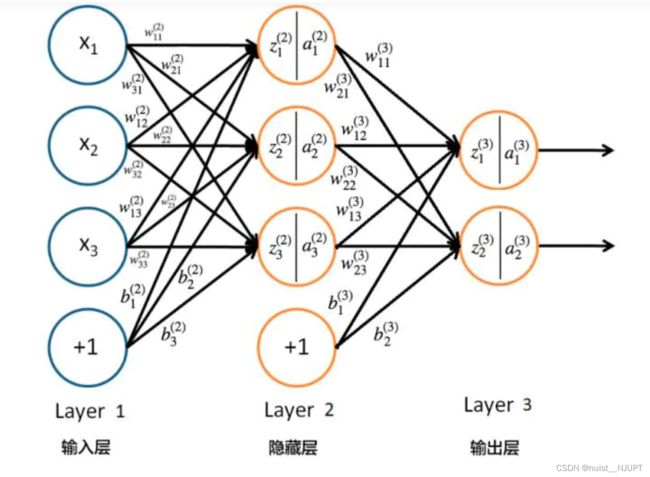
我们首先看一下BP神经网络，BP 网络的实现过程主要分成两个阶段，第一阶段是信号的前向传播，从输入层经过隐含层到达输出层，第二阶段是误差的反向传播，从输出层经过隐含层到达输入层。误差传递完后，依次调节输入层和隐含层之间的权值和偏置，以及隐含层和输出层之间的权值和偏置。如图所示：

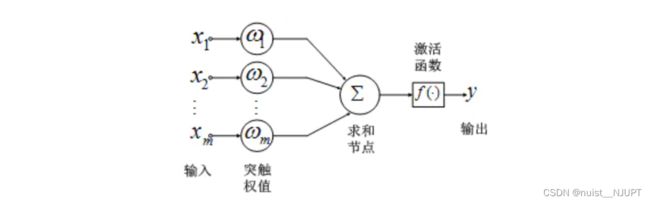
 BP神经网络的神经元如下所示，一般使用的激活函数是sigmoid函数，如下：

 

小波变换是以 Fourier 分析为基础的一种新的数学变换手段，它克服了 Fourier变换的局限性以及加窗 Fourier 变换的窗口不变的缺点。小波变换主要通过伸缩和平移实现多尺度细化，突出所要处理的问题细节，有效提取局部信息。小波神经网络是改进的BP网络，将原先的隐含层的Sigmiod激活函数替换为小波函数——Morlet小波，其表达式为：

1.2、小波神经网络建立

我们看一下这个小波神经网络，相比BP神经网络，将原先的隐含层的Sigmiod激活函数替换为小波函数。

 

 

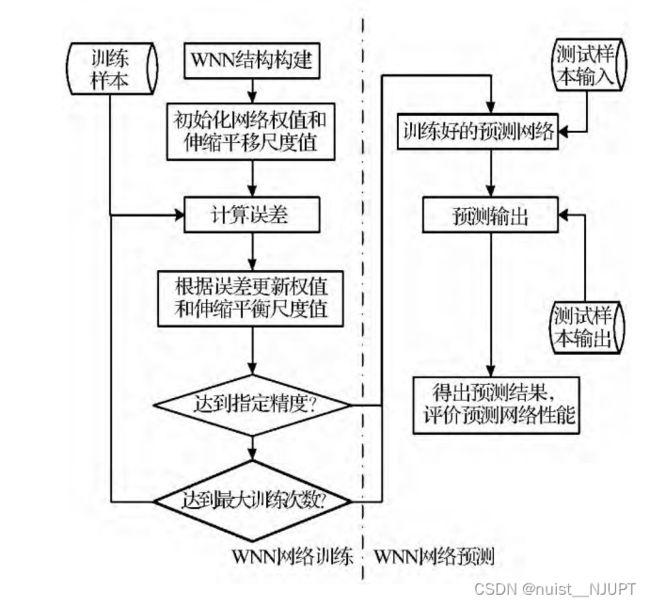
 1.3、小波神经网络的预测流程图

小波神经网络的预测过程如下，初始化网络权值和伸缩平移尺度等参数，计算误差，根据误差调整参数，根据训练集训练出较好的网络，然后根据网络进行预测。

 

1.4、数据集准备

数据划分为训练集数据和测试集数据，训练276组，测试集92组，输入为交通相关的四个参数，输出是交通流量。

 1.5、小波神经网络预测短时交通流MATLAB代码及结果分析

 下面看一下小波神经网络的matlab代码：

%% 清空环境变量
clc
clear

%% 网络参数配置
load traffic_flux input output input_test output_test

M=size(input,2); %输入节点个数
N=size(output,2); %输出节点个数

n=6; %隐藏层节点个数
lr1=0.01; %学习速率
lr2=0.001; %学速率速率
maxgen=100; %迭代次数

%初始化输入层到隐含层，隐含层到输出层的权值
Wjk=randn(n,M);Wjk_1=Wjk;Wjk_2=Wjk_1;
Wij=randn(N,n);Wij_1=Wij;Wij_2=Wij_1;
%初始化伸缩因子
a=randn(1,n);a_1=a;a_2=a_1;
b=randn(1,n);b_1=b;b_2=b_1;

%节点初始化
y=zeros(1,N);
net=zeros(1,n);
net_ab=zeros(1,n);

%权值学习增量初始化
d_Wjk=zeros(n,M);
d_Wij=zeros(N,n);
d_a=zeros(1,n);
d_b=zeros(1,n);

%% 输入输出数据归一化
[inputn,inputps]=mapminmax(input');
[outputn,outputps]=mapminmax(output'); 
inputn=inputn';
outputn=outputn';

%% 网络训练
for i=1:maxgen
    %误差累计
    error(i)=0;
    % 循环训练
    for kk=1:size(input,1)
        x=inputn(kk,:);
        yqw=outputn(kk,:);
        for j=1:n
            for k=1:M
                net(j)=net(j)+Wjk(j,k)*x(k);
                net_ab(j)=(net(j)-b(j))/a(j);
            end
            temp = exp(-(net_ab(j).^2)/2) * cos(1.75*net_ab(j));
            %temp=mymorlet(net_ab(j)); %小波函数
            for k=1:N
                y=y+Wij(k,j)*temp;   %计算输出
            end
        end
        
        %计算误差和
        error(i)=error(i)+sum(abs(yqw-y));
        
        %权值调整
        for j=1:n
            %计算d_Wij，隐藏层和输出层权值调整
            temp=exp(-(net_ab(j).^2)/2) * cos(1.75*net_ab(j));
            for k=1:N
                d_Wij(k,j)=d_Wij(k,j)-(yqw(k)-y(k))*temp;
            end
            %计算d_Wjk，输入层到隐藏层权值调整
            temp = -1.75*sin(1.75*net_ab(j)).*exp(-(net_ab(j).^2)/2)-net_ab(j)* cos(1.75*net_ab(j)).*exp(-(net_ab(j).^2)/2) ;
      
            for k=1:M
                for l=1:N
                    d_Wjk(j,k)=d_Wjk(j,k)+(yqw(l)-y(l))*Wij(l,j) ;
                end
                d_Wjk(j,k)=-d_Wjk(j,k)*temp*x(k)/a(j);
            end
            %计算d_b，伸缩因子
            for k=1:N
                d_b(j)=d_b(j)+(yqw(k)-y(k))*Wij(k,j);
            end
            d_b(j)=d_b(j)*temp/a(j);
            %计算d_a，伸缩因子
            for k=1:N
                d_a(j)=d_a(j)+(yqw(k)-y(k))*Wij(k,j);
            end
            d_a(j)=d_a(j)*temp*((net(j)-b(j))/b(j))/a(j);
        end
        
        %权值参数更新      
        Wij=Wij-lr1*d_Wij;
        Wjk=Wjk-lr1*d_Wjk;
        b=b-lr2*d_b;
        a=a-lr2*d_a;
    
        d_Wjk=zeros(n,M);
        d_Wij=zeros(N,n);
        d_a=zeros(1,n);
        d_b=zeros(1,n);

        y=zeros(1,N);
        net=zeros(1,n);
        net_ab=zeros(1,n);
        
        Wjk_1=Wjk;Wjk_2=Wjk_1;
        Wij_1=Wij;Wij_2=Wij_1;
        a_1=a;a_2=a_1;
        b_1=b;b_2=b_1;
    end
end

%% 网络预测
%预测输入归一化
x=mapminmax('apply',input_test',inputps);
x=x';

%网络预测
for i=1:92
    x_test=x(i,:);

    for j=1:1:n
        for k=1:1:M
            net(j)=net(j)+Wjk(j,k)*x_test(k);
            net_ab(j)=(net(j)-b(j))/a(j);
        end
        temp=exp(-(net_ab(j).^2)/2) * cos(1.75*net_ab(j));
        for k=1:N
            y(k)=y(k)+Wij(k,j)*temp ; 
        end
    end

    yuce(i)=y(k);
    y=zeros(1,N);
    net=zeros(1,n);
    net_ab=zeros(1,n);
end
%预测输出反归一化
ynn=mapminmax('reverse',yuce,outputps);

%% 结果分析
figure(1)
plot(ynn,'r*:')
hold on
plot(output_test,'bo--')
title('预测交通流量','fontsize',12)
legend('预测交通流量','实际交通流量')
xlabel('时间点')
ylabel('交通流量')

这次使用了两个Morlet小波函数：用来更新各层之间的权重和伸缩因子。

y = exp(-(t.^2)/2) * cos(1.75*t);

y = -1.75*sin(1.75*t).*exp(-(t.^2)/2)-t* cos(1.75*t).*exp(-(t.^2)/2) ;

预测的效果如下所示，可以发现使用测试集进行预测，预测的交通流量和实际的交通流量较为接近，网络模型的泛化能力较好。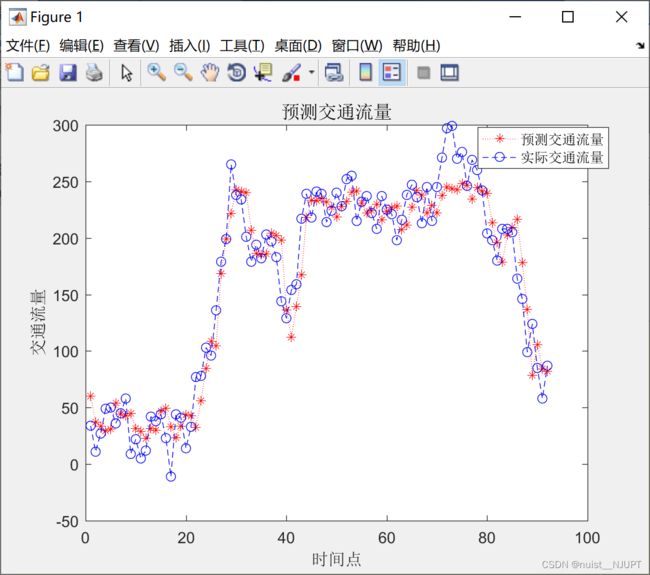

 

1.6、小结

小波神经网络（Wavelet Neural Network， WNN）是在小波分析研究获得突破的基础上提出的一种人工神经网络。它是基于小波分析理论以及小波变换所构造的一种分层的、多分辨率的新型人工神经网络模型。即用非线性小波基取代了通常的非线性Sigmoid 函数，其信号表述是通过将所选取的小波基进行线性叠加来表现的。它避免了BP 神经网络结构设计的盲目性和局部最优等非线性优化问题，大大简化了训练，具有较强的函数学习能力和推广能力及广阔的应用前景。