支持向量机----核技巧(Kernel Trick)

升维转换

支持向量机模型强大的另一个原因是能够解决非线性分类问题，通过升维转换的方式将 n 维数据转化为 n+1 维数据，从而构建决策超平面进行分类。

如下图的这种分类问题

可见上图，具有两种不同的数据点的类别，分别为蓝色(1)、红色(-1),显然在此2维平面内无法找出一个直线对这两个类别进行有效分类。

这个时候应该如何实现对这两类数据点进行分类呢?

我们可以为这些数据点进行维度升级，即从2维数据升级至3维数据，即$\begin{array}{rl}(x_1,x_2)& \Rightarrow (x_1,x_2,x_1^2+x_2^2)\end{array}$，之后再使用决策超平面进行构建分类器。

如下图:

这样我们便可以使用支持向量机进行构建决策超平面进行数据点分类了。

升维转化后的最优值求解

我们已经知道支持向量机的最优化(最大间隔)的公式为(如有不解，请点击)

$$max(-\frac{\sum _{i=1}^s\sum _{j=1}^s{\lambda }_i{\lambda }_j{y}_i{y}_j\ast x_i\cdot x_j}{2}+\sum _{i=1}^s{\lambda }_i)$$

当进行升维转化后，发生了以下变化

$$\begin{array}{rl}(x_1,x_2)& \Rightarrow (x_1,x_2,x_1^2+x_2^2)\end{array}$$

我们可以把升维转化通过**函数$T(x)$**来表示，即

$$\begin{array}{rl}x& \Rightarrow T(x)\end{array}$$

所以，升维转化后的最优化(最大间隔)的公式为

$$max(-\frac{\sum _{i=1}^s\sum _{j=1}^s{\lambda }_i{\lambda }_j{y}_i{y}_j\ast T(x_i)\cdot T(x_j)}{2}+\sum _{i=1}^s{\lambda }_i)$$

如何进行升维转化

从n维数据转化为n+1维数据并求解 $T(x_i)\cdot T(x_j)$ 有两种方式

1、 自定义维数升级函数 $T(x)$，再计算$T(x_i)\cdot T(x_j)$

2、 直接使用核函数进行计算 $K(x_i,x_j)$

自定义维度升级函数 $T(x)$，并利用向量内积求解

这种方法是直接定义维度转化函数，将低维数据升级至高维数据，再利用向量内积计算结果，如下例

$$\begin{array}{rl}x=(x_1,x_2)& \Rightarrow T(x)=(1,\sqrt{2}{x}_1,\sqrt{2}{x}_2,x_1^2,x_2^2,\sqrt{2}{x}_1{x}_2)\end{array}$$

该维度转化函数将原来的二维数据转化为六维数据，现在计算内积结果(计算内积结果的目的是可以求解最优化间隔)：

$$T(x_i)\cdot T(x_j)=(1+2x_{i1}{x}_{j1}+2x_{i2}{x}_{j2}+x_{i1}^2{x}_{j1}^2+x_{i2}^2{x}_{j2}^2+2x_{i1}{x}_{j1}{x}_{i2}{x}_{j2})$$

之后再代入最优化间隔公式即可。

但是这种方式无法处理无限维度的数据，且需要人工定义维度转化函数，故大多数时候不采用。

核函数 $K(x_i,x_j)$ 直接计算

直接套用多项式核函数(见下)进行计算

$$\begin{array}{rl}K(x_i,x_j)& =(1+x_i\cdot x_j{)}^2\\ & =(1+(x_{i1}{x}_{j1}+x_{i2}{x}_{j2}){)}^2\\ & =(1+2x_{i1}{x}_{j1}+2x_{i2}{x}_{j2}+x_{i1}^2{x}_{j1}^2+x_{i2}^2{x}_{j2}^2+2x_{i1}{x}_{j1}{x}_{i2}{x}_{j2})\end{array}$$

可见，两种方式计算的结果最终一致。

核函数(Kernel Function)

核函数是用来计算升维转换后的 $x_i^{\ast }\cdot y_i^{\ast }$ ，便于最优化间隔的计算，有利于构成决策超平面。

以下介绍两种最常用的核函数，分别为多项式核函数、高斯核函数(RBF)。

多项式核函数

多项式核函数的一般形式为

$$K(x_i,x_j)=(c+x_i\cdot x_j{)}^d$$

不同的参数c和d能够控制转换后的维度数和空间相似度，进而影响最终的决策超平面结果。

多项式核函数的参数c十分重要，正是因为它的存在，最终的点积结果表达式中才包含了从低次项到高次项的数据组合，体现了维度的多样性。

若无常数量c，可结合多个多项式核函数丰富维度的多样性。

高斯核函数(RBF)

高斯核函数的一般形式为

$$K(x_i,x_j)=e^{-\gamma ||x_i-x_j|{|}^2}$$

该结果一般会反映两向量的相似度大小，决定因素为一个大于0的 $\gamma$ 值和两向量坐标点间的距离共同决定。

当调整 $\gamma$ 值的大小时，它对应的变化如下

当 $\gamma =1$ 时，数据点的距离越大，相似度越趋于0，且图像是平滑的，即样本数据会被简单的决策超平面划分。

当 $\gamma =50$ 时，只有当数据点的距离足够小时，相似度才为1，否则均为0，图像是尖窄的，即样本数据会被复杂的决策超平面划分。

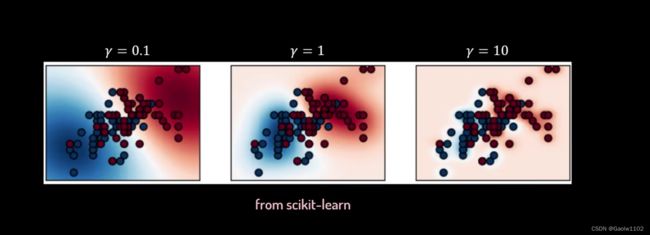
如下图，不同的 $\gamma$ 对应不同的划分方式，其中红、蓝代表两个不同的类别

所以在高斯核函数中选择合适的 $\gamma$ 值变得尤其重要。

另外，高斯核函数的另外一个优势是可以应用到无限维度的数据样本中，我们尝试着把它变换一下(这里令 $\gamma =0.5$ ):

$$\begin{array}{rl}K(x_i,x_j)& =e^{-\gamma ||x_i-x_j|{|}^2}\\ & =e^{-\frac{1}{2}(x_i-x_j)(x_i-x_j)}\\ & =e^{-\frac{1}{2}(||x_i|{|}^2+||x_j|{|}^2-2x_i{x}_j)}\\ & =e^{-\frac{1}{2}(||x_i|{|}^2+||x_j|{|}^2)}{e}^{x_i\cdot x_j}\end{array}$$

这里令 $C=e^{-\frac{1}{2}(||x_i|{|}^2+||x_j|{|}^2)}$，故原式转化为:

$$K(x_i,x_j)=C{e}^{x_i\cdot x_j}$$

使用泰勒展开式 $e^x=\sum _{n=0}^{\infty }\frac{x^n}{n!}=1+x+\frac{x^2}{2}+...+\frac{x^n}{n!}$ 对高斯核函数进行展开，得

$$K(x_i,x_j)=C(1+x_i\cdot x_j+\frac{(x_i\cdot x_j{)}^2}{2}+...+\frac{(x_i\cdot x_j{)}^n}{n!})$$

证明得之，高斯核函数确实能够应用在无限维度的样本数据中(理想情况)。

小结

支持向量机的核技巧(Kernel Trick)通过维度转换能够很有效地解决数据分类的问题。

但往往对参数的设置十分敏感，在实际情景中应用时应作适当调整。