Secret-Key Encryption Lab网安实验
Secret-Key Encryption Lab网安实验
实验站点
文章目录
- Secret-Key Encryption Lab网安实验
-
- Task 1: Frequency Analysis Against Monoalphabetic Substitution Cipher
- Task 2: Encryption using Different Ciphers and Modes
- Task 3: Encryption Mode – ECB vs. CBC
-
- -aes-128-ecb
- -aes-128-cbc
- Task 4: Padding
- Task 5: Error Propagation – Corrupted Cipher Text
-
- ECB
- CBC
- CFB
- OFB
- Task 6: Initial Vector (IV)
- Task 7: Programming using the Crypto Library
Task 1: Frequency Analysis Against Monoalphabetic Substitution Cipher
It is well-known that monoalphabetic substitution cipher (also known as monoalphabetic cipher) is not secure, because it can be subjected to frequency analysis. In this lab, you are given a cipher-text that is encrypted using a monoalphabetic cipher; namely, each letter in the original text is replaced by another letter, where the replacement does not vary (i.e., a letter is always replaced by the same letter during the encryption). Your job is to find out the original text using frequency analysis. It is known that the original text is an English article.
In the following, we describe how we encrypt the original article, and what simplification we have made. Instructors can use the same method to encrypt an article of their choices, instead of asking students to use the ciphertext made by us.
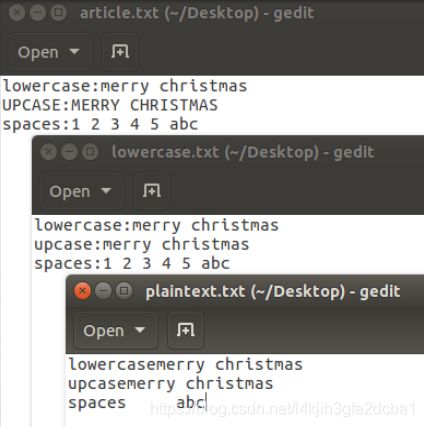
- Step 1: let us do some simplification to the original article. We convert all upper cases to lower cases, and then removed all the punctuations and numbers. We do keep the spaces between words, so you can still see the boundaries of the words in the ciphertext. In real encryption using monoalphabetic cipher, spaces will be removed. We keep the spaces to simplify the task. We did this using the following command:
$ tr [:upper:] [:lower:] < article.txt > lowercase.txt
$ tr -cd ’[a-z][\n][:space:]’ < lowercase.txt > plaintext.txt
- Step 2: let us generate the encryption key, i.e., the substitution table. We will permute the alphabet from a to z using Python, and use the permuted alphabet as the key. See the following program.
$ python
>>> import random
>>> s = "abcdefghijklmnopqrstuvwxyz"
>>> list = random.sample(s, len(s))
>>> ’’.join(list)
’sxtrwinqbedpvgkfmalhyuojzc’
- Step 3: we use the tr command to do the encryption. We only encrypt letters, while leaving the space and return characters alone.
$ tr ’abcdefghijklmnopqrstuvwxyz’ ’sxtrwinqbedpvgkfmalhyuojzc’ \
< plaintext.txt > ciphertext.txt
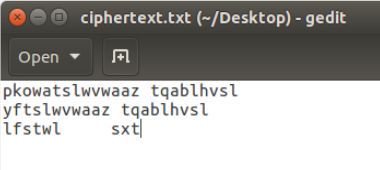
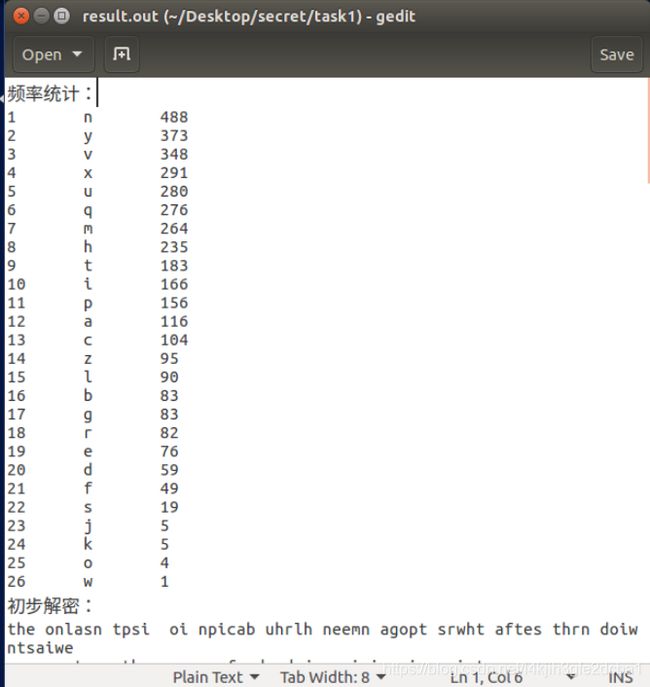
We have created a ciphertext using a different encryption key (not the one described above). You can download it from the lab’s website. Your job is to use the frequency analysis to figure out the encryption key and the original plaintext.
ciphertext.txt
//cpp11
//需要提前创建"result.out"
#include 总结:可以正常统计出各个字母的出现频率并根据公开单字母频率制作对照表,但似乎仍未能正确解密原文,推测还需要制作双字母对照表,限于时间未能进一步完善。
Task 2: Encryption using Different Ciphers and Modes
In this task, we will play with various encryption algorithms and modes. You can use the following openssl enc command to encrypt/decrypt a file. To see the manuals, you can type man openssl and man enc.
$ openssl enc -ciphertype -e -in plain.txt -out cipher.bin \
-K 00112233445566778889aabbccddeeff \
-iv 0102030405060708
-ciphertype可以选择想要使用的加密方式
Please replace the ciphertype with a specific cipher type, such as -aes-128-cbc, -bf-cbc, -aes-128-cfb, etc. In this task, you should try at least 3 different ciphers. You can find the meaning of the command-line options and all the supported cipher types by typing “man enc”. We include some common options for the openssl enc command in the following:
-in input file
-out output file
-e encrypt
-d decrypt
-K/-iv key/iv in hex is the next argument
-[pP] print the iv/key (then exit if -P)
使用案例:
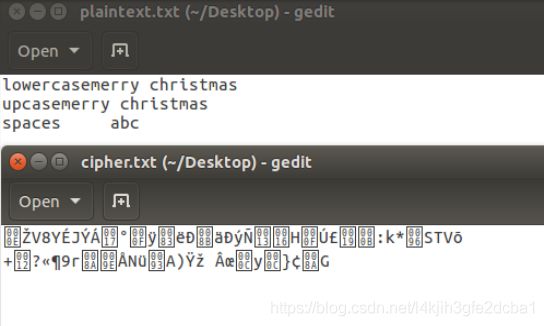
$ openssl enc -des -e -in ./plaintext.txt -out cipher.bin -K 0011223344 -iv 0102030405060708
Task 3: Encryption Mode – ECB vs. CBC
The file pic original.bmp can be downloaded from this lab’s website, and it contains a simple picture. We would like to encrypt this picture, so people without the encryption keys cannot know what is in the picture. Please encrypt the file using the ECB (Electronic Code Book) and CBC (Cipher Block Chaining) modes, and then do the following:
pic_original.bmp
-aes-128-ecb
加密指令:
openssl enc -aes-128-ecb -in ./pic_original.bmp -out ./p2.bmp -e -K 12345678
-aes-128-cbc
加密指令:
openssl enc -aes-128-cbc -in ./pic_original.bmp -out ./p_cbc.bmp -e -K 12345678 -iv 12345678
- Let us treat the encrypted picture as a picture, and use a picture viewing software to display it. However, For the .bmp file, the first 54 bytes contain the header information about the picture, we have to set it correctly, so the encrypted file can be treated as a legitimate .bmp file. We will replace the header of the encrypted picture with that of the original picture. We can use the bless hex editor tool (already installed on our VM) to directly modify binary files. We can also use the following commands to get the header from p1.bmp, the data from p2.bmp (from offset 55 to the end of the file), and then combine the header and data together into a new file.
$ head -c 54 ./pic_original.bmp >header
$ tail -c +55 p_ecb.bmp > ecb_body
$ tail -c +55 p_cbc.bmp > cbc_body
$ cat header ecb_body > newECB.bmp
$ cat header cbc_body > newCBC.bmp
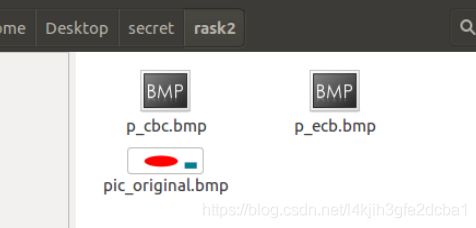
- Display the encrypted picture using a picture viewing program (we have installed an image viewer program called eog on our VM). Can you derive any useful information about the original picture from the encrypted picture? Please explain your observations.
Observation:
越是复杂的图片加密的效果越好,但ECB的加密强度会比CBC差很多,这点可以由简单图片的加密得出。
Task 4: Padding
For block ciphers, when the size of a plaintext is not a multiple of the block size, padding may be required. All the block ciphers normally use PKCS#5 padding, which is known as standard block padding. We will conduct the following experiments to understand how this type of padding works:
1.Use ECB, CBC, CFB, and OFB modes to encrypt a file (you can pick any cipher). Please report which modes have paddings and which ones do not. For those that do not need paddings, please explain why.
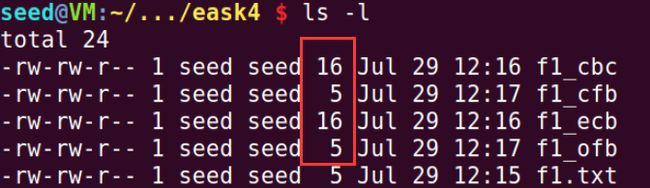
$ echo -n "12345" > f1.txt
$ openssl enc -aes-128-ecb -in f1.txt -out f1_ecb -e -K 12345678
$ openssl enc -aes-128-cbc -in f1.txt -out f1_cbc -e -K 12345678 -iv 12345678
$ openssl enc -aes-128-cfb -in f1.txt -out f1_cfb -e -K 12345678 -iv 12345678
$ openssl enc -aes-128-ofb -in f1.txt -out f1_ofb -e -K 12345678 -iv 12345678
ECB、CBC出现填充,CFB、OFB没有填充。因为CFB、OFB可以将DES转换为流密码。
2.Let us create three files, which contain 5 bytes, 10 bytes, and 16 bytes, respectively. We can use the following “echo -n” command to create such files. The following example creates a file f1.txt with length 5 (without the -n option, the length will be 6, because a newline character will be added by echo):
$ echo -n "12345" > f1.txt
We then use “openssl enc -aes-128-cbc -e” to encrypt these three files using 128-bit AES
with CBC mode. Please describe the size of the encrypted files.

We would like to see what is added to the padding during the encryption. To achieve this goal, we will decrypt these files using “openssl enc -aes-128-cbc -d”. Unfortunately, decryption by default will automatically remove the padding, making it impossible for us to see the padding.
However, the command does have an option called “-nopad”, which disables the padding, i.e., during the decryption, the command will not remove the padded data. Therefore, by looking at the decrypted data, we can see what data are used in the padding. Please use this technique to figure out what paddings are added to the three files.
It should be noted that padding data may not be printable, so you need to use a hex tool to display the content. The following example shows how to display a file in the hex format:
$ hexdump -C p1.txt
#00000000 31 32 33 34 35 36 37 38 39 49 4a 4b 4c 0a |123456789IJKL.|
$ xxd p1.txt
#00000000: 3132 3334 3536 3738 3949 4a4b 4c0a 123456789IJKL.
作者选择使用xxd
xxd第一部分为这一行第一个byte的位置;
xxd第二部分为这一行ASCII码转十六进制
xxd第三部分为这一行原本的内容
根据输出,我们发现,CBC的填充内容每个字节都为该行的大小与满编的距离,例如该行有5字节,则空余部分每个字节均填充(0x10-0x05)=0x0b=11
Task 5: Error Propagation – Corrupted Cipher Text
To understand the error propagation property of various encryption modes, we would like to do the following exercise:
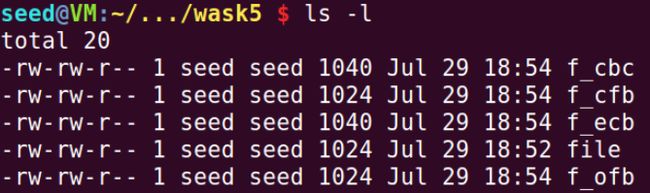
- Create a text file that is at least 1000 bytes long.
- Encrypt the file using the AES-128 cipher.
- Unfortunately, a single bit of the 55th byte in the encrypted file got corrupted. You can achieve this corruption using the bless hex editor.
- Decrypt the corrupted ciphertext file using the correct key and IV.
Please answer the following question: How much information can you recover by decrypting the corrupted file, if the encryption mode is ECB, CBC, CFB, or OFB, respectively? Please answer this question before you conduct this task, and then find out whether your answer is correct or wrong after you finish this task. Please provide justification.
预测:
ECB将只有第四组解密错误
CBC将有第四组与第五组的解密错误
CFB根据加解密的设置不同可造成影响不同,但至少当前组与下一组组将出现错误
OFB将只有当前组解密错误
如图依次完成4份加密文件的修改,以下为进入bless的方法
bless xxx.txt
ECB
如图,ECB加密方式64bit为一组,其中一个字节出现错误,整组解密均错误
CBC
如图,当前一组64bit均解密错误,并且因为与下一组进行异或,下一组的第7个字节出现错误
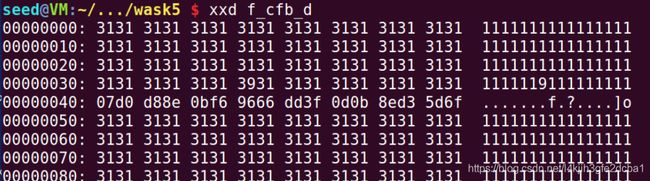
CFB
如图,当前组与流密码异或,第55个字节出现错误,但该组进入下一组的移位寄存器参与AES,使得下一组整组错误
OFB
如图,OFB不存在扩散问题,且因为与流密码异或加密,所以一个字节错误不会影响整组的解密错误,仅第55字节错误
Task 6: Initial Vector (IV)
Most of the encryption modes require an initial vector (IV). Properties of an IV depend on the cryptographic scheme used. If we are not careful in selecting IVs, the data encrypted by us may not be secure at all, even though we are using a secure encryption algorithm and mode. The objective of this task is to help students understand the problems if an IV is not selected properly. Please do the following experiments:
- Task 6.1. A basic requirement for IV is uniqueness, which means that no IV may be reused under the same key. To understand why, please encrypt the same plaintext using (1) two different IVs, and (2) the same IV. Please describe your observation, based on which, explain why IV needs to be unique.
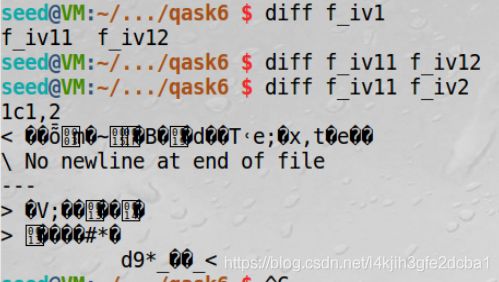
$ openssl enc -aes-128-ofb -in file -out f_iv11 -K 12345678 -iv 12345678
$ openssl enc -aes-128-ofb -in file -out f_iv12 -K 12345678 -iv 12345678
$ openssl enc -aes-128-ofb -in file -out f_iv2 -K 12345678 -iv 87654321
可以发现,在相同key下,使用相同iv将导致加密结果相同,使用iv等于变相增强加密密钥的复杂度
- Task 6.2. One may argue that if the plaintext does not repeat, using the same IV is safe. Let us look at the Output Feedback (OFB) mode. Assume that the attacker gets hold of a plaintext (P1) and a ciphertext (C1) , can he/she decrypt other encrypted messages if the IV is always the same? You are given the following information, please try to figure out the actual content of P2 based on C2, P1, and C1.
Plaintext (P1): This is a known message!
Ciphertext (C1): a469b1c502c1cab966965e50425438e1bb1b5f9037a4c159
Plaintext (P2): (unknown to you)
Ciphertext (C2): bf73bcd3509299d566c35b5d450337e1bb175f903fafc159
P1保存为文件,C1C2保存为二进制文件
P2=P1 ⨁ \bigoplus ⨁C1 ⨁ \bigoplus ⨁C2
使用python对P1 C1 C2的三份二进制文件进行异或,得到P2的二进制为4f726465723a204c61756e63682061206d697373696c6521

If we replace OFB in this experiment with CFB (Cipher Feedback), how much of P2 can be revealed? You only need to answer the question; there is no need to demonstrate that.
如果是CFB,那么视iv的长度得到可以解密的长度,长于iv的内容都无法正常解密。
因为已知明文攻击可以通过异或得到iv但是无法得到K值,那么使用CFB加密,攻击者将在解出K前无法算出流密码,即无法解密接下来的内容。相反,已知明文后攻击OFB无需得到K即可获得长度相当于明文的流密码,只要K与iv不变,可以攻击任何长度不大于已知明文长度的密文。
The attack used in this experiment is called the known-plaintext attack, which is an attack model for cryptanalysis where the attacker has access to both the plaintext and its encrypted version (ciphertext). If this can lead to the revealing of further secret information, the encryption scheme is not considered as secure.
- Task 6.3. From the previous tasks, we now know that IVs cannot repeat. Another important requirement on IV is that IVs need to be unpredictable for many schemes, i.e., IVs need to be randomly generated. In this task, we will see what is going to happen if IVs are predictable.
Assume that Bob just sent out an encrypted message, and Eve knows that its content is either Yes or No; Eve can see the ciphertext and the IV used to encrypt the message, but since the encryption algorithm AES is quite strong, Eve has no idea what the actual content is. However, since Bob uses predictable IVs, Eve knows exactly what IV Bob is going to use next. The following summarizes what Bob and Eve know:
Encryption method: 128-bit AES with CBC mode.
Key (in hex): 00112233445566778899aabbccddeeff (known only to Bob)
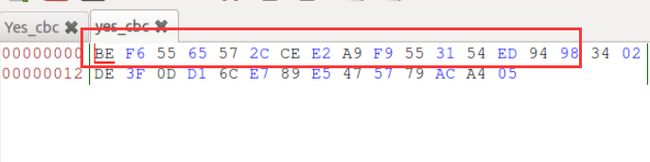
Ciphertext (C1): bef65565572ccee2a9f9553154ed9498 (known to both)
IV used on P1 (known to both)
(in ascii): 1234567890123456
(in hex) : 31323334353637383930313233343536
Next IV (known to both)
(in ascii): 1234567890123457
(in hex) : 31323334353637383930313233343537
A good cipher should not only tolerate the known-plaintext attack described previously, it should also tolerate the chosen-plaintext attack, which is an attack model for cryptanalysis where the attacker can obtain the ciphertext for an arbitrary plaintext. Since AES is a strong cipher that can tolerate the chosen-plaintext attack, Bob does not mind encrypting any plaintext given by Eve; he does use a different IV for each plaintext, but unfortunately, the IVs he generates are not random, and they can always be predictable.
Your job is to construct a message P2 and ask Bob to encrypt it and give you the ciphertext. Your objective is to use this opportunity to figure out whether the actual content of P1 is Yes or No.
已知Bob的明文有两种情况:(1)“Yes”(2)“No”。
根据task5我们知道, “Yes”在CBC加密中会被补全到16字节:59 65 73 0D 0D 0D 0D 0D 0D 0D 0D 0D 0D 0D 0D 0D 。“No”会被补全为:4E 6F 0E 0E 0E 0E 0E 0E 0E 0E 0E 0E 0E 0E 0E 0E
因为Bob的明文只有两种情况,所以我们可以先假设上一条明文为Yes,构造P2验证C2与Yes加密后结果相同,若不同则上一条为No。
所以我们构造的P2(Yes)的十六进制形式为:59 65 73 0D 0D 0D 0D 0D 0D 0D 0D 0D 0D 0D 0D 0C。(P2(No)的十六进制形式为4E 6F 0E 0E 0E 0E 0E 0E 0E 0E 0E 0E 0E 0E 0E 0F)注意到我们只修改了最后一个字节。将我们构造的P2发送给Bob请求加密,并与C1比对即可得知上一条密文的明文。
我们根据task5可以知道16字节文件加密会被补全到32字节,但根据CBC加密特点,我们只需要关注前16个字节即可,后16字节对结果无影响
对“Yes”的猜测回文:
对“No”的猜测回文:
Task 7: Programming using the Crypto Library
This task is mainly designed for students in Computer Science/Engineering or related fields, where programming is required. Students should check with their professors to see whether this task is required for their courses or not.
In this task, you are given a plaintext and a ciphertext, and your job is to find the key that is used for the encryption. You do know the following facts:
- The aes-128-cbc cipher is used for the encryption.
- The key used to encrypt this plaintext is an English word shorter than 16 characters; the word can be found from a typical English dictionary. Since the word has less than 16 characters (i.e. 128 bits), pound signs (#: hexadecimal value is 0x23) are appended to the end of the word to form a key of 128 bits.
Your goal is to write a program to find out the encryption key. You can download a English word list from the Internet. We have also linked one on the web page of this lab. The plaintext, ciphertext, and IV are listed in the following:
Plaintext (total 21 characters): This is a top secret.
Ciphertext (in hex format): 764aa26b55a4da654df6b19e4bce00f4ed05e09346fb0e762583cb7da2ac93a2
IV (in hex format): aabbccddeeff00998877665544332211
You need to pay attention to the following issues:
- If you choose to store the plaintext message in a file, and feed the file to your program, you need to check whether the file length is 21. If you type the message in a text editor, you need to be aware that some editors may add a special character to the end of the file. The easiest way to store the message in a file is to use the following command (the -n flag tells echo not to add a trailing newline):
$ echo -n "This is a top secret." > file
- In this task, you are supposed to write your own program to invoke the crypto library. No credit will be given if you simply use the openssl commands to do this task. Sample code can be found from the following URL:
https://www.openssl.org/docs/man1.0.2/crypto/EVP_EncryptInit.html - When you compile your code using gcc, do not forget to include the -lcrypto flag, because your code needs the crypto library. See the following example:
$ gcc -o myenc myenc.c -lcrypto
话不多说,先上代码:
// main.cpp
#include 如图,答案是Syracuse