【数学建模】“一口价”的战略（博弈模型）

问题背景

商店推出一种销售策略：双方同时报价，若顾客的出价大于商家卖价则成交，价格为双方出价的均值，否则不成交。在此情况下，双方应如何报价？

模型假设

1.商家知道商品对自己的真实价值$v_s$，也就是可以卖出的最低价格；顾客知道商品对自己的真实价值$v_b$，也就是可以支付的最高价格。
2.商家不知道商品对顾客的真实价值$v_b$，但知道其概率分布；顾客不知道商品对商家的真实价值$v_s$，但也知道其概率分布。
3.不妨假设$v_s,v_b$都服从[0,1]上的均匀分布。
4.对一组给定的$(v_s,v_b)$如果以价格$p$成交，该交易对商家和顾客的效用分别为$p-v_s$，$v_b-p$；如果不成交，双方的效用均为0.商家和顾客都希望最大化自己的期望效用。
5.以上信息为双方所共有。

模型建立

记商家的战略为$p_s(v_s)$，即当商家认为商品的价值为$v_s$时，他给出卖价$p_s(v_s)$；记顾客的战略为$p_b(v_b)$，即当顾客认为商品的价值为$v_b$时，他给出报价$p_b(v_b)$。自然地，$p_b(v_b)$和$p_s(v_s)$都应该是定义在[0,1]区间上、取值也在[0,1]区间上的非减函数。

对于任意给定的 $v_s\in [0,1]$，商家的报价$p_s(v_s)$应该使其期望利润最大。因为只有$p_b(v_b)\ge p_s(v_s)$时才能成交，成交后商家的利润为$(p_s(v_s)+p_b(v_b))/2-v_s$，而不成交时利润为0，所以$p_s(v_s)$应满足
$$\underset{p_s}{\max }\left\{\frac{p_s+E[p_b(v_b)|p_b(v_b)\ge p_s]}{2}-v_s\right\}P\left\{p_b(v_b)\ge p_s\right\}（1）$$
类似地，对于任意给定的$v_b\in [0,1]$，顾客的报价 $p_b(v_b)$ 应该使其期望赢得最大，成交后顾客的赢得为 $v_b-(p_s(v_s)+p_b(v_b))/2$，不成交时赢得为0，所以$p_b(v_b)$应满足
$$\underset{p_b}{\max }\left\{v_b-\frac{p_b+E[p_s(v_s)|p_b\ge p_s(v_s)]}{2}\right\}P\left\{p_b\ge p_s(v_s)\right\}（2）$$

如果战略组合$(p_s(v_s),p_b(v_b))$满足（1）和（2），则是双方的一个均衡，对于这个博弈问题存在很多均衡，下面介绍其中两个比较简单的均衡。

单一价格均衡

设定(0,1)区间上一个数x，商家如果认为商品的价值$v_s\le x$，则报价x，否则报价为1；顾客如果认为商品的价值$v_b\ge x$，则报价x，否则报价为0.这种价格战略可表示为
$$p_s(v_s)=\{\begin{array}{ll}x,& v_s\le x\\ 1,& v_s>x\end{array}(3)$$
$$p_b(v_b)=\{\begin{array}{ll}x,& v_b\ge x\\ 0,& v_b<x\end{array}(4)$$

观察可得，战略组合$(p_s(v_s),p_b(v_b))是同时满足（1）和（2）$

首先，可以注意到成交价格只能发生在x。
此外，从商家的角度看，如果顾客坚持战略（4），则商家在$v_s\le x$时报价x是他的最优反应。因为报价低于x显然使自己的利润降低（假设能成交）；而报价高于x则不能成交，自己本来可以从成交中获得的利润不能实现。如果$v_s>x$，则成交会使商家利润为负，商家当然不希望成交，而报价为1可以保证不成交。因此战略（3）是商家对顾客的战略（4）的最优反应。
同理，如果商家坚持战略（3），战略（4）是顾客的最优反应。因此，（3）和（4）是一个均衡，称为单一价格均衡。

对一组给定的$(v_b,v_s)$，当$v_b<v_s$时称为交易时有利的，因为此时一定存在$p\in (v_s,v_b)$，当双方以价格$p$交易时，对双方都是有利的（由模型假设4），交易给双方带来的效用之和（即$v_b-v_s$）称为交易价值。在给定的战略组合下，能够实际发生的交易的期望与有利的全部交易的期望价值的比值称为该战略的交易效率。

下面分析单一价格战略的交易效率，显然，当且仅当 $v_s\le x\le v_b$时，交易实际上才能发生。若$v_s,v_b$都服从[0,1]上的均匀分布，图1中对角线上的三角形时交易有利的区域，而蓝色矩形区域才是交易实际发生的区域，所以交易效率为：
$$\eta =\frac{{\int }_x^1\mathrm{d}{v}_b{\int }_0^x(v_b-v_s)\mathrm{d}{v}_s}{{\int }_0^1\mathrm{d}{v}_b{\int }_0^{v_b}(v_b-v_s)\mathrm{d}{v}_s}$$

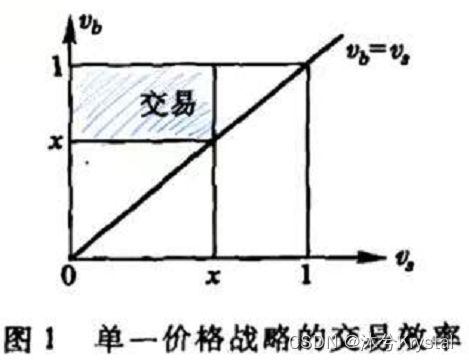
显然，当$x=0.5$时交易效率最大，但最大效率也只有3/4。

线性价格均衡

假设商家和顾客的报价分别是商品对二者价值的线性函数，表示为
$$\begin{gathered} p_s(v_s)=a_s+c_s{v}_s(6) \\ {p}_b(v_b)=a_b+c_b{v}_b(7) \end{gathered}$$
我们需要确定其中的系数（不妨假设均为正数）$a_s,c_s,a_b,c_b$，使这个战略组合$(p_s(v_s),p_b(v_b))$同时满足（1）和（2），即构成一个均衡。

假设商家的战略为(6)，由假设3知$p_s$服从$[a_s,a_s+c_s]$上的均匀分布，此时对于给定的$v_b$，顾客的最优反应就是寻找满足（2）式的$p_b$。当$p_b\in [a_s,a_s+c_s]$时，$P\left\{p_b\ge p_s(v_s)\right\}=(p_b-a_s)/c_s,E[p_s|p_b\ge p_s]=(a_s+p_b)/2$，于是（2）式为
$$\underset{p_b}{\max }\left\{v_b-\frac{p_b+(a_s+p_b)/2}{2}\cdot \frac{p_b-a_c}{c_s}\right\}$$
这是一个二次函数的优化，其最优解为
$$p_b=\frac{2}{3}{v}_b+\frac{1}{3}{a}_s$$
类似的，求解过程如下图：

评注

这里讨论的模型一般称为双向拍卖，是一个同时出价的博弈（静态博弈），而且是信息不完全（双方的真实价值是各自的私有信息，对方只知道其分布），所以是一个不完全信息静态博弈。可以看出，这个问题不仅是对某个具体交易（给定的$v_s,v_b$）提供报价决策，而是要对所有可能的$v_s,v_b$提供一个报价方案$(p_s(v_s),p_b(v_b))$，这才是一个均衡（战略组合）。对不完全信息静态博弈，这样的均衡一般称为贝叶斯均衡或贝叶斯-纳什均衡。