声谱图,梅尔语谱,倒谱,梅尔倒谱系数
常用的频域音频特征
语音特征提取。声音信号本是一维的时域信号,直观上很难看出频率变化规律。傅里叶变换可把它变到频域上,虽然可看出信号的频率分布,但是丢失了时域信息,无法看出频率分布随时间的变化。为了解决这个问题,很多时频分析手段应运而生,如短时傅里叶,小波,Wigner分布等都是常用的时频域分析方法。
频谱图、相位频谱图
将一段信号做离散傅里叶变换后,将频率作为横轴,幅度为纵轴,得到的就是频谱图。
将一段信号做离散傅里叶变换后,将频率作为横轴,相位为纵轴,得到的就是相位频谱图。
声谱图 / 语谱图(spectrogram)
首先从理论上:
对于一段语音信号x(t),
(1)首先加窗分帧,变为x(m,n)。(n为帧长,m为帧的个数);
(2)然后做FFT变换,得到X(m,n),做周期图Y(m,n)(Y(m,n) = X(m,n) * X(m,n)');

能量密度谱函数Pn(w)是二维的非负实值函数。也是信号的自相关函数的STFT。

其中,短时自相关函数:

用时间n作为横坐标,w作为纵坐标,将Pn(w)的值表示为灰度级所构成的二维图像即语谱图(Spectrogram)。
语谱图是表示语音频谱随时间变化的图形,其纵轴为频率,横轴为时间,任一给定频率成分在给定时刻的强弱用相应点的灰度或色调来表示。语谱图中显示了大量与语音的语句特性有关的信息,它综合了频谱图和时域波形的点,明显地显示出语音频谱随时间的变化情况,或者说是一种动态的频谱。目前,现代的语谱图阅读技术已经显示出语谱图中包含有充足的语音学信息,一些语音学家能够用其语音学知识,从语谱图上可见的发声特征来解释语谱图。语谱图中的花纹有横杠、乱纹等。浊音一般对应横杠,横杠所在之处是基音频率或者基音频率的整数倍,而清音从语谱图上看,表现为乱纹。在一个语音段的语谱图中,有没有横杠出现是判断它是否是浊音的重要标志。
下面从物理意义上直观讲解:
短时傅里叶变换(STFT)是最经典的时频域分析方法。所谓短时傅里叶变换,顾名思义,是对短时的信号做傅里叶变化。那么短时的信号怎么得到的? 是长时的信号分帧得来的。STFT的原理非常简单,把一段长信号分帧、加窗,再对每一帧做傅里叶变换(FFT),最后把每一帧的结果沿另一个维度(频域)堆叠起来(旋转90度),得到类似于一幅图的二维信号形式。然后把这些幅度映射到一个灰度级表示(也可以理解为将连续的幅度量化为256个量化值?),0表示黑,255表示白色。幅度值越大,相应的区域越黑。这样就得到了最右边的图。那为什么要这样呢?为的是增加时间这个维度,这样就可以显示一段语音而不是一帧语音的频谱,而且可以直观的看到静态和动态的信息。
从下图来看,语语谱(spectrogram),实际上就是把每帧的频谱图向左旋转90度,用颜色的深浅表示幅度的大小,幅度越大颜色越深,然后把每帧的颜色信息按照时间(帧)的顺序列出来,所以,语谱的横坐标为时间(帧),纵坐标为频率,颜色为频率的幅度。
注意: 频率和时间值是离散的,每个代表一个“bin”,而振幅是实值。颜色显示在离散坐标(时间,频率)振幅的实值。
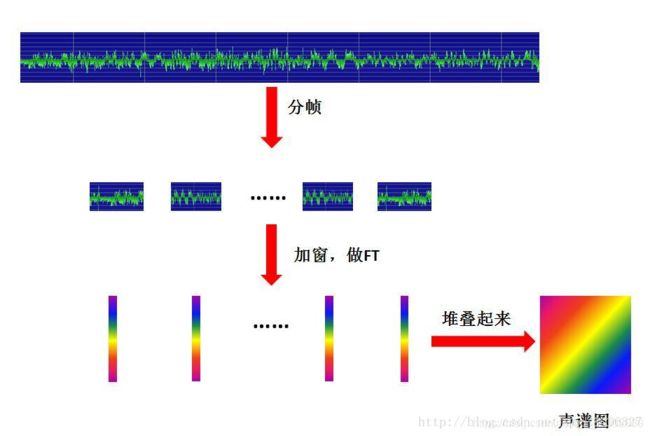
这个过程中,需要注意的有两点,一个是帧长,对于使用较短的帧,其具有较宽的频带(宽带语谱图),较高的时间分辨率和较低的频率分辨率,而对于较长的帧,则具有较窄的频带(窄带语谱图),较低的时间分辨率和较高的频率分辨率;另一点要注意的是为了是帧与帧之间的过渡更加平稳,采用了帧移的方法,即两帧之间有个重叠区域。
语谱图分类:
- 宽带语谱图(45Hz):良好的时间分辨率,能给出语音的共振峰频率及清辅音的能量汇聚区,共振峰呈现黑色条纹;
- 窄带语谱图(300Hz):良好的频率分辨率,有利于显示基音频率和各次谐波,不利于观察共振峰(声道变化)。

语谱图的本质就是确定不同说话人声音的本性。横坐标为时间,纵坐标为频率。图中的条纹称之为“声纹”,它因人而异,即可利用声纹鉴别不同的说话人。有横杠(Bar),乱纹,和竖直条等花纹。 - 横杠是与时间轴平行的几条深黑色带纹,它们相应于短时谱中的几个凸点,也就是共振峰,从横杠对应的频率和带宽可以确定相应的共振峰频率和带宽。在一个语音段的语谱图中,是否有横杠出现是判断他是否是浊音的重要标志。
- 竖直条(又叫冲直条),是与时间轴垂直的一条窄黑条,每个竖直条相当于一个基音,条纹的起点相当于声门脉冲的起点,条纹之间的距离代表基音周期,条纹越密说明基音频率越高。
- 元音一般对应横杠,它代表共振峰的存在。清擦音在语谱图中表现为乱纹,乱纹的深浅,上下限反映了噪声能量在频域中的分布。
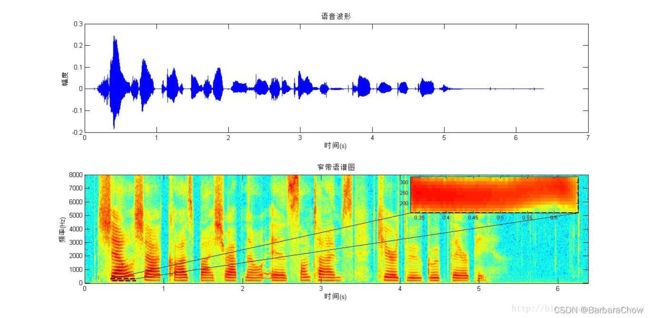
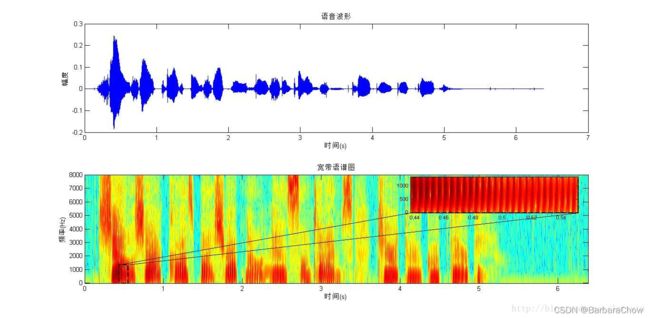
下面分别展示了一条语音句子的窄带语谱图和宽带语谱图。短时窗长度分别是20ms和2ms。
窄带:都是横纹。所以频率分辨率高。
宽带:都是竖纹。所以时间分辨率高。
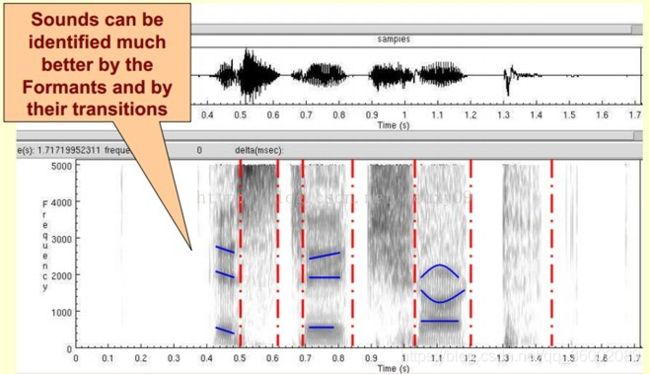
下图是一段语音的声谱图,很黑的地方就是频谱图中的峰值(共振峰formants)
语谱图优点:
音素(Phones)的属性可以更好的在这里面观察出来。
通过观察共振峰和它们的转变可以更好的识别声音。
隐马尔科夫模型(Hidden Markov Models)就是隐含地对声谱图进行建模以达到好的识别性能。还有一个作用就是它可以直观的评估TTS系统(text to speech)的好坏,直接对比合成的语音和自然的语音声谱图的匹配度即可。
梅尔频谱 / 梅尔语谱(Mel-spectrogram)
语谱图往往是很大的一张图,为了得到合适大小的声音特征,往往把它通过梅尔标度滤波器组(mel-scale filter banks),变换为梅尔频谱。
人耳听到的声音高低和实际(Hz)频率不呈线性关系,用Mel频率更符合人耳的听觉特性(这正是用Mel声谱图的一个动机,由人耳听力系统启发),即在1000Hz以下呈线性分布,1000Hz以上呈对数增长,Mel频率与Hz频率的关系为:
fmel=2595⋅lg(1+f/700Hz)。
有另一种计算方式为fmel=1125⋅ln(1+f700Hz)。
python中可以用librosa调包得到梅尔声谱图。

上图是HZ到Mel的映射关系图,可以看到二者为log关系,在频率较低时,Mel随HZ变化较快;当频率较高时,曲线斜率小,变化缓慢。
mel-specotrogram提取步骤:
- 提取信号的STFT
- 将amplitude转换为DBs(10log|s|^2)
- 将频率转换到mel尺度(mel-bands个数选择,构建mel滤波器组)
mel bands个数选择多少合适?
常见的有40,60,90,128等,具体问题具体选择。
构建mel滤波器组:
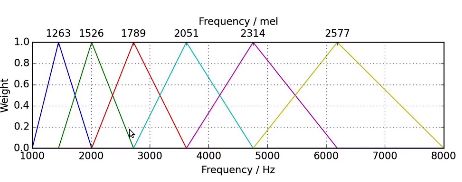
mel滤波器组形状:M = (bands, framesize / 2 +1)
信号频谱形状:Y = (framesize /2 +1, frames)
bands:mel滤波器个数;framesize每帧长;frames:帧数
那么,
Mel spectrogram = MY (bands, frames)
mel语谱图的应用:

倒谱(cepsrum)
倒谱一词是频谱spectrum英文的前四个单词倒过来写而构成的。下面是一个语音的频谱图(FT)。峰值表示语音的主要频率成分,我们把这些峰值称为共振峰(formants),而共振峰就是携带了声音的辨识属性(就是个人身份证一样)。
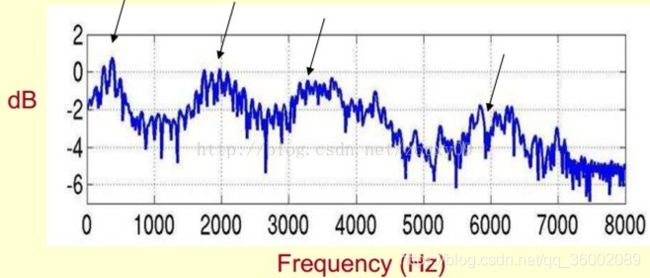
提取共振峰:要提取的不仅仅是共振峰的位置,还得提取它们转变的过程。所以我们提取的是频谱的包络(Spectral Envelope)。这包络就是一条连接这些共振峰点的平滑曲线。
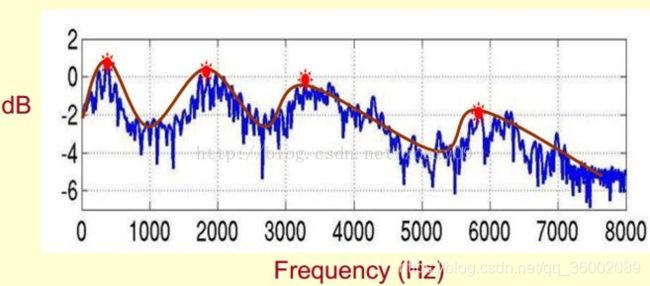
可以这么理解,将原始的频谱由两部分组成:包络和频谱的细节。这里用到的是对数频谱,所以单位是dB。那现在我们需要把这两部分分离开,这样我们就可以得到包络了。
那怎么把他们分离开呢?也就是,怎么在给定log X[k]的基础上,求得log H[k] 和 log E[k]以满足log X[k] = log H[k] + log E[k]呢?
即:同态信号处理。它的目的是将非线性问题转化为线性问题的处理方法。
1)将原语音信号经过傅里叶变换得到频谱:X[k]=H[k]E[k];
(时域卷积–频域乘积)只考虑幅度就是:|X[k] |=|H[k]||E[k] |;
2)我们在两边取对数:log||X[k] ||= log ||H[k] ||+ log ||E[k] ||。(乘性–加性)
3)再在两边取逆傅里叶变换得到:x[k]=h[k]+e[k]。
在对数频谱上面做IFFT就相当于在一个伪频率(pseudo-frequency)坐标轴上面描述信号。所以虽然是时域序列,但它们所处的离散时域显然不同,此时称为倒谱频域。
x[k]实际上就是倒谱Cepstrum。(这个是一个新造出来的词,把频谱的单词spectrum的前面四个字母顺序倒过来就是倒谱的单词了)。而我们所关心的h[k]就是倒谱的低频部分。h[k]描述了频谱的包络,它在语音识别中被广泛用于描述特征。
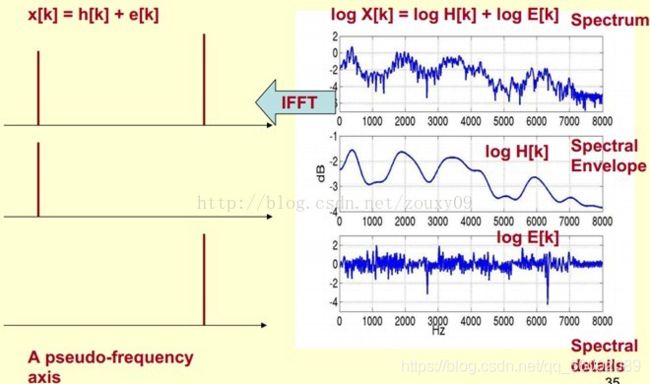
总结下,倒谱(cepstrum)就是一种信号的傅里叶变换经对数运算后再进行傅里叶反变换得到的谱。它的计算过程如下:

梅尔倒谱系数(Mel-Frequency Cepstral Coefficients, MFCC)
我们将频谱通过一组Mel滤波器就得到Mel频谱。公式表述就是:
log X[k] = log (Mel-Spectrum)。这时候我们在log X[k]上进行倒谱分析:
1)取对数:log X[k] = log H[k] + log E[k]。
2)进行逆变换:x[k] = h[k] + e[k]。
在Mel频谱上面获得的倒谱系数h[k]就称为Mel频率倒谱系数,简称MFCC。
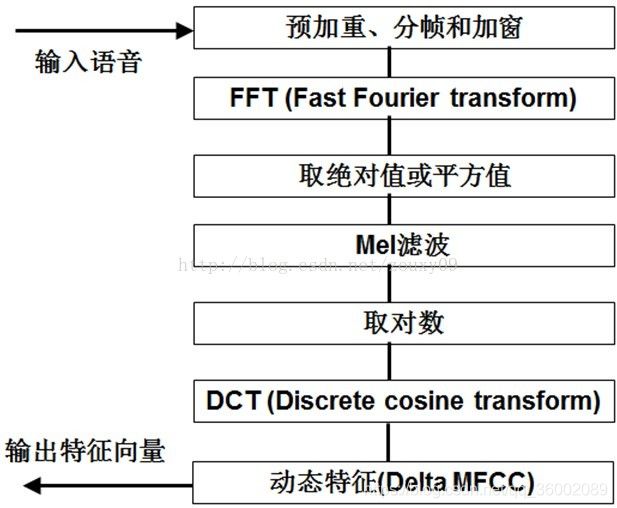
完整的MFCC及其动态特征提取过程:
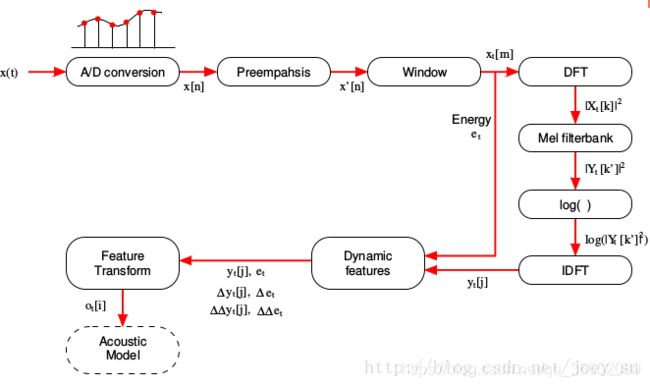
MFCC特征为什么要做DCT,而一般不做反傅里叶IDFT?
DCT可以看作是IDFT的简化版,DCT得到的是实值系数,而FFT会返回复数值,但这里复数系数并不太需要。mel滤波器组有很多重叠部分,DCT可以在不同的mel频带上去相关性,因为在机器学习中,希望输入的特征之间的相关性越小越好。而且DCT相当于是对log mel谱的降维。
总结如下:

mel滤波器组:
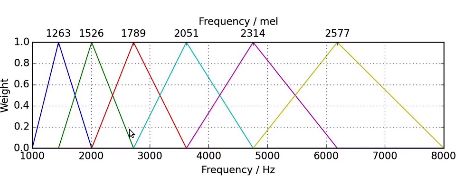
需要选择多少个系数?
因为一般只关注声道信息,即谱包络成分(低频),语音识别中不太需要声门激励信息,也就是谱细节(高频),因为声道信息才是包含了我们感兴趣的成分,如音素信息,共振峰等,所以一般选前12-13个系数。当然你也可以选择更多系数,但可能对算法性能提升并不大。一般为了提高机器学习模型性能,会选择一阶和二阶MFCC,因为delta(MFCC)会与前一帧相减,还会取delta(delta(MFCC)),这样每帧差不多就共有13*3=39个系数。

上图是个可视化的MFCC图,选了16个系数。
感知线性预测(Perceptual linear prediction, PLP)
知线性预测(PLP)技术最早发表于1990年,其感知体现在巴克刻度、临界频带、等响度曲线和幂函数等对人耳听觉感知的建模上。
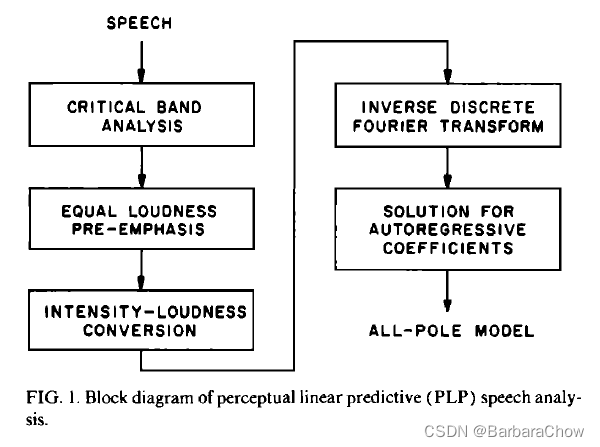
(1)分帧加窗。原始论文建议帧长20ms,汉明窗。
(2)对每帧进行FFT,帧长不是2的整数次幂补零即可,得时频谱。
(3)将幅值平方,得功率谱。
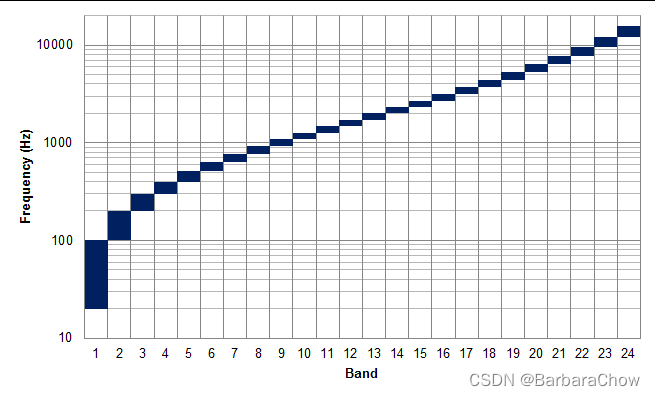
(4)输入巴克滤波器组(预先设计好的临界频带critical-band),目的是校正人耳听觉对频率的非线性。
(5)通过等响度曲线预加重equal-loudness preemphasis,校正人耳对不同频率的敏感度。

(6)用幂函数校正人耳对于声强的非线性intensity-loudness power law。
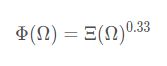
(7)逆DFT,从而得到线性预测编码系数。
总结
1.频谱:时域信号(一维)傅里叶变换后的频域信号(一维)。
2.声谱图/语谱图:时域信号(一维)短时傅里叶变换后的时频信号(二维)。
3.倒谱:也叫做倒频谱,二次谱,对数功率谱等。对声谱图取对数后,再DFT变回时域,此时不是完全意义上的时域,应叫做倒谱域。
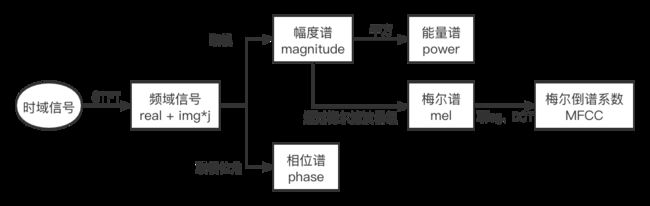
4.MFCC:对线性声谱图应用mel滤波器后,取log,得到log梅尔声谱图,然后对log滤波能量(log梅尔声谱)做DCT离散余弦变换(傅里叶变换的一种),然后保留第2到第13个系数,得到的这12个系数就是MFCC。
附加:
1.能量谱:也叫做能量密度谱。是原信号傅里叶变化的平方。用于描述时间序列的能量随频率的分布。
2.功率谱:将频谱或时频谱(语谱)中的幅值进行平方,得到功率谱。
3.功率谱密度:定义为单位频带内的吸纳后功率。其推导公式较为复杂,但维纳-辛欣定理证明了:一段信号的功率谱等于 这段信号自相关函数的傅里叶变换。
注:信号分为确定和随机,确定信号又分为能量和功率,随机信号一定是功率信号。语音信号是随机信号。


