2017年高教社杯全国大学生数学建模竞赛题目--C题 颜色与物质浓度辨识
问题
比色法是目前常用的一种检测物质浓度的方法,即把待测物质制备成溶液后滴在特定的白色试纸表面,等其充分反应以后获得一张有颜色的试纸,再把该颜色试纸与一个标准比色卡进行对比,就可以确定待测物质的浓度档位了。由于每个人对颜色的敏感差异和观测误差,使得这一方法在精度上受到很大影响。随着照相技术和颜色分辨率的提高,希望建立颜色读数和物质浓度的数量关系,即只要输入照片中的颜色读数就能够获得待测物质的浓度。试根据附件所提供的有关颜色读数和物质浓度数据完成下列问题:
- 附件Data1.xls中分别给出了5种物质在不同浓度下的颜色读数,讨论从这5组数据中能否确定颜色读数和物质浓度之间的关系,并给出一些准则来评价这5组数据的优劣。
- 对附件Data2.xls中的数据,建立颜色读数和物质浓度的数学模型,并给出模型的误差分析。
- 探讨数据量和颜色维度对模型的影响。
已给条件:
1、附件表中的浓度ppm也称百万分比浓度,表示每升体积纯水(或溶剂)中待测物质所含的毫克数(mg/L),
即ppm=mg/L,经常用于浓度很小的场合。如:组胺浓度为50ppm 表示每升组胺溶液中含组胺50毫克。
表中"水":表示待测物质浓度为零的情形。
2、附件表中的变量B、G、R、H、S含义:
B(Blue):蓝色颜色值
G(Green):绿色颜色值
R(Red):红色颜色值
H(Hue): 色调
S(Saturation):饱和度

分析
第一问:
分析附件Data1.xls里的数据可知,颜色的数据是用RGB模式表示,即用:红 、绿、蓝三种颜色的数值,共同得出真实颜色的数值。通过在网上的查找,可以使用一下公式计算颜色值:颜色值 = 65536Red+256Green+Blue。然后我有了解了色调和饱和度的概念。
色调:色调是指图像的相对明暗程度,在彩色图像上表现为颜色。在rgb中色调越低,颜色更加偏向于红色。色调越高,颜色更加偏向于蓝色。
饱和度:饱和度决定了颜色空间中颜色分量,饱和度越高,说明颜色越深,饱和度越低,说明颜色越浅。
R方:确定系数,是通过数据的变化来表征一个拟合的好坏。由上面的表达式可以知道“确定系数”的正常取值范围为[0 1],越接近1,表明方程的变量对y的解释能力越强,这个模型对数据拟合的也较好.
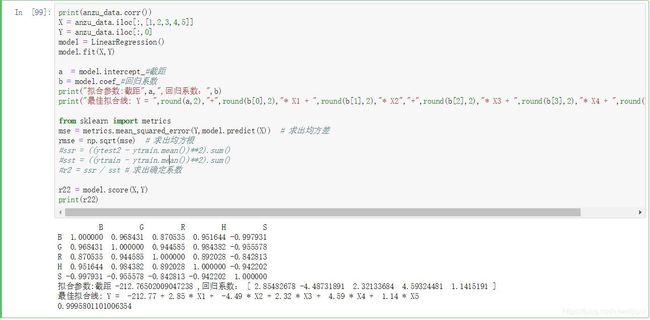
首先,通过利用pandas库里的corr函数,得到所给数据满足线性关系,所以我建立多元线性回归模型。最后准则我选择确定系数(即R方),通过比较五组数据的拟合程度,进而比较五组数据的准确性。
我分别对每种物质的数据进行多元线性回归,并求其R方值
数据导入和分析
组胺:

溴酸钾

工业碱


硫酸铝钾:


奶中尿素


根据R值可知:拟合行从好到坏:组胺>溴酸钾>奶中尿素>工业碱>硫酸铝钾
所以优劣排序为:组胺>溴酸钾>奶中尿素>工业碱>硫酸铝钾
第二问
题目要求对Data2.xls中的数据进行分析,并建立颜色读数和物质浓度的数学模型。首先,我们还先对Data2.xls中的数据进行处理,并建立多元线性回归模型,得出其最佳拟合曲线和确定系数。

数据导入和处理
第三问
首先我们分析数据量对模型的影响:
我们拿附件Data1.xls中具有代表性的两组数据,即硫酸铝钾和组胺,分析数据量对模型的影响。
首先是拟合效果最好的组胺:
由于其只有两组数据,所以我们每次去除一组浓度值,第一次我们去除了浓度为12.5的两组数据,第二次我们去除了浓度为100的两组数据,第三次我们又去除了浓度为50的两组数据。
| 数据量 | R2 | 模型检验 |
|---|---|---|
| 10 | 0.99958 | 成立 |
| 8 | 0.99982 | 成立 |
| 6 | 1 | 不成立 |
其次是数据量最多的硫酸铝钾:
由于硫酸铝钾数据很多,所以我们每次删除每种浓度里的一组数据。每次删除6个数据
| 数据量 | R2 | 模型检验 |
|---|---|---|
| 37 | 0.46866 | 成立 |
| 31 | 0.44771 | 成立 |
| 25 | 0.39343 | 不成立 |
| 19 | 0.47690 | 不成立 |
| 13 | 0.69584 | 不成立 |
综上所述,实验量不能太高或者太低,太高会导致数据错误较多,误差变大,数据太小会导致数据真实性不足。
颜色维度的结果没有算出来!!!
论文
第一问
论文也使用了多元线性回归的模型,但是其对模型的判断指标,除了我选择的R2之外,还有F 检验、 P 值、估计误差方差 S2
F检验: 对于多元线性回归模型,在对每个回归系数进行显著性检验之前,应该对回归模型的整体做显著性检验。这就是F检验。
样本标准偏差的平方,即:
S2=∑(x- x的平均数)2/(n-1)
两组数据就能得到两个S2值
F=S2/S2’
然后计算的F值与查表得到的F表值比较,如果
F < F表 表明两组数据没有显著差异;
F ≥ F表 表明两组数据存在显著差异。
估计误差方差 S2:
在统计学中,估计误差是此估计量的期望值与估计参数的真值之差。误差为零的估计量或决策规则称为无偏的。否则该估计量是有偏的。
同时,他在进行多元线性回归之前,还删除了一些明显存在错误的数据,所以其得到的R2和拟合效果比我的好的多。
第二问
论文也首先使用了多元线性回归模型,进行曲线拟合,但是模型的残差较大,拟合效果不佳。所以又使用了以下四个模型:①linear(线性)②purequadratic(纯二次) ③interaction(交叉)④quadratic(完全二次)。
rstool 函数输出包括回归参数,剩余标准差以及残差,可以通过修改
model 的值比较多个模型的标准差来确定哪个最好。
最终论文采用完全二次的方法进行多元非线性二次回归
第三问
本篇论文中,把颜色维度分成了:五维(rgbhs)三维(rgb)二维(hs)一维(r)一维(g)一维(b)一维(h)一维(s)
然后拿所给数据,根据不同的维度,进行曲线拟合,分别列出不同维度下曲线拟合的R2,F 检验、 P 值、和估计误差方差 S2,综合分析不同维度对结果的影响。最后得出 进一步 对比发
颜色维度的大小比数据量的多少对模型的影响更大
然后,它还利用了层次分析法对数据量和颜色维度对模型的影响因子进行求解得出数据量和颜色维度对模型的影响因子分别为 0.414 和0.586。最后得出模型评价的层次结构模型。
