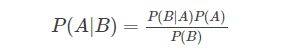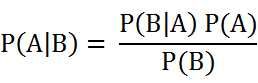机器学习笔记——朴素贝叶斯(Naive Bayes)
1贝叶斯算法简介
贝叶斯分类算法是统计学的一种分类方法,它是一类利用概率统计知识进行分类的算法。在许多场合,朴素贝叶斯(Naïve Bayes,NB)分类算法可以与决策树和神经网络分类算法相媲美,该算法能运用到大型数据库中,而且方法简单、分类准确率高、速度快。
1.1贝叶斯算法优点
优点:在数据较少时仍有效,可处理多类别问题
1.2贝叶斯算法缺点
缺点:对输入数据准备方式敏感,如果输入的数据的各个特征之间是具有关联的,那么分类的效果可能不佳,反之,如果各个特征之间的关联度不大,则分类效果才可能不错
1.3贝叶斯算法思想
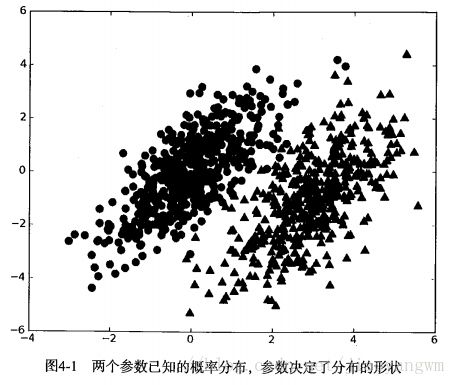
假设现在我们有一个数据集,它由两类数据组成,数据分布如上图所示:
我们现在用p1(x,y)表示数据点(x,y)属于类别1(图中圆点表示的类别)的概率,用p2(x,y)表示数据点(x,y)属于类别2(图中三角形表示的类别)的概率,那么对于一个新数据点(x,y),可以用下面的规则来判断它的类别:
如果p1(x,y) > p2(x,y),那么类别为1
如果p1(x,y) < p2(x,y),那么类别为2
也就是说,我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想,即选择具有最高概率的决策。
适用决策树不会非常成功,和简单的概率计算相比,KNN计算量太大,因此对于上述问题,最佳选择是概率比较方法。
接下来,就是学习如何计算p1和p2概率。
2.概率公式
2.1 条件概率
条件概率(Condittional probability),就是指在事件B发生的情况下,事件A发生的概率,用P(A|B)来表示。
2.2 全概率
3 朴素贝叶斯定理
3.1贝叶斯推导
对条件概率进行变形:
我们把P(A)称为”先验概率”(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。
P(A|B)称为”后验概率”(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。
P(B|A)/P(B)称为”可能性函数”(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。
所以,条件概率可以理解成下面的式子:
后验概率=先验概率∗调整因子后验概率=先验概率∗调整因子
这就是贝叶斯推断的含义:我们先预估一个”先验概率”,然后加入实验结果,看这个实验到底是增强还是削弱了”先验概率”,由此得到更接近事实的”后验概率”。
在这里,如果”可能性函数”P(B|A)/P(B)>1,意味着”先验概率”被增强,事件A的发生的可能性变大;如果”可能性函数”=1,意味着B事件无助于判断事件A的可能性;如果”可能性函数”<1,意味着”先验概率”被削弱,事件A的可能性变小。
3.2朴素贝叶斯概念
“朴素”的解释:假设各个特征之间相互独立(在贝叶斯分类器上做了简化)
朴素贝叶斯的基础假设:
①每个特征相互独立;
②每个特征的权重(或重要性)都相等,即对结果的影响程度都相同。
3.2朴素贝叶斯计算条件概率
4.实现代码
4.1词表到向量转换函数
把文本看成 单词向量 或者 词条向量,也就是说将句子转换为向量。考虑出现在所有文档中的所有单词,再决定将哪些词纳入词汇表或者说所要的词汇集合,然后必须要将每一篇文档转换为词汇表上的向量。简单起见,先假设已经将本文切分完毕,存放到列表中,并对词汇向量进行分类标注。
def loadDataSet():
"""
Function: 创建实验样本
Args: 无
Returns: postingList:词条切分后的文档集合
classVec:类别标签的集合
"""
#词条切分后的文档集合
postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
#类别标签的集合
classVec = [0,1,0,1,0,1] #1 is abusive, 0 not
#词条切分后的文档集合和类别标签结合
return postingList,classVec
def createVocabList(dataSet):
"""
Function: 创建一个包含所有文档中出现的不重复词的列表
Args: dataSet:数据集
Returns: list(vocabSet):返回一个包含所有文档中出现的不重复词的列表
"""
#创建一个空集
vocabSet = set([])
#将新词集合添加到创建的集合中
for document in dataSet:
#操作符 | 用于求两个集合的并集
vocabSet = vocabSet | set(document)
#返回一个包含所有文档中出现的不重复词的列表
return list(vocabSet)
def setOfWords2Vec(vocabList, inputSet):
"""
Function: 词表到向量的转换
Args: vocabList:词汇表
inputSet:某个文档
Returns: returnVec:文档向量
"""
#创建一个所含元素都为0的向量
returnVec = [0]*len(vocabList)
#遍历文档中词汇
for word in inputSet:
#如果文档中的单词在词汇表中,则相应向量位置置1
if word in vocabList:
returnVec[vocabList.index(word)] = 1
#否则输出打印信息
else: print("the word: %s is not in my Vocablary!" % word)
#向量的每一个元素为1或0,表示词汇表中的单词在文档中是否出现
return returnVec- postingList 是原始的 词条列表;
- VocabList 是 词汇表,是所有单词出现的集合,没有重复的元素;一个单词在词汇表中出现过一次,那么就在相应位置记作1,如果没有出现就在相应位置记作0。
- setOfWords2Vec(vocabList, inputSet)则根据vocabList词汇表,将inputSet向量化,向量的每个元素为1或0
4.2朴素贝叶斯分类器训练函数
依照4.1我们将一组单词转换为一组数字,现在知道一个词是否出现在一篇文档中,也知道该文档所属的类别。这时重写贝叶斯准则,将之前的B、A 替换为w。粗体w表示这是一个向量,即它由多个数值组成。
![]()
假设所有词都互相独立,该假设也称作条件独立性假设,对每个类计算该值,然后比较这两个概率值的大小。 p0V和p1V存放的就是VocabList中单词的条件概率,举个例子p0V存放的是属于类别0的单词的概率,也就是非侮辱类词汇的概率。而pAb就是文档属于侮辱类的概率
def trainNB0(trainMatrix, trainCategory):
"""
Function: 朴素贝叶斯分类器训练函数
Args: trainMatrix:文档矩阵
trainCategory:类别标签向量
Returns: p0Vect:非侮辱性词汇概率向量
p1Vect:侮辱性词汇概率向量
pAbusive:侮辱性文档概率
"""
#获得训练集中文档个数
numTrainDocs = len(trainMatrix)
#获得训练集中单词个数
numWords = len(trainMatrix[0])
#计算文档属于侮辱性文档的概率
pAbusive = sum(trainCategory)/float(numTrainDocs)
#初始化概率的分子变量
p0Num = zeros(numWords); p1Num = zeros(numWords)
#初始化概率的分母变量
p0Denom = 0.0; p1Denom = 0.0
#遍历训练集trainMatrix中所有文档
for i in range(numTrainDocs):
#如果侮辱性词汇出现,则侮辱词汇计数加一,且文档的总词数加一
if trainCategory[i] ==1:
p1Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
#如果非侮辱性词汇出现,则非侮辱词汇计数加一,且文档的总词数加一
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
#对每个元素做除法求概率
p1Vect = p1Num/p1Denom
p0Vect = p0Num/p0Denom
#返回两个类别概率向量和一个概率
return p0Vect, p1Vect, pAbusive4.3朴素贝叶斯分类函数
通过classifyNB()方法就可以利用 p0V和p1V和pAb数据将待分类的词条数组进行分类。
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
"""
Function: 朴素贝叶斯分类函数
Args: vec2Classify:文档矩阵
p0Vec:非侮辱性词汇概率向量
p1Vec:侮辱性词汇概率向量
pClass1:侮辱性文档概率
Returns: 1:侮辱性文档
0:非侮辱性文档
"""
#向量元素相乘后求和再加到类别的对数概率上,等价于概率相乘
p1 = sum(vec2Classify * p1Vec) + log(pClass1)
p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)
#分类结果
if p1 > p0:
return 1
else:
return 0
def testingNB():
"""
Function: 朴素贝叶斯分类器测试函数
Args: 无
Returns: testEntry:测试词汇列表
classifyNB(thisDoc, p0V, p1V, pAb):分类结果
"""
#从预先加载中调入数据
listOPosts, listClasses = loadDataSet()
#构建一个包含所有词的列表
myVocabList = createVocabList(listOPosts)
#初始化训练数据列表
trainMat = []
#填充训练数据列表
for postinDoc in listOPosts:
trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
#训练
p0V, p1V, pAb = trainNB0(trainMat, listClasses)
#测试
testEntry = ['love', 'my', 'dalmation']
thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
print(testEntry,'classified as: ', classifyNB(thisDoc, p0V, p1V, pAb))
#测试
testEntry = ['stupid', 'garbage']
thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
print(testEntry,'classified as: ', classifyNB(thisDoc, p0V, p1V, pAb))4.4构建词袋模型
def bagOfWords2VecMN(vocabList, inputSet):
"""
Function: 词袋到向量的转换
Args: vocabList:词袋
inputSet:某个文档
Returns: returnVec:文档向量
"""
#创建一个所含元素都为0的向量
returnVec = [0]*len(vocabList)
#将新词集合添加到创建的集合中
for word in inputSet:
#如果文档中的单词在词汇表中,则相应向量位置加1
if word in vocabList:
returnVec[vocabList.index(word)] += 1
#返回一个包含所有文档中出现的词的列表
return returnVec4.5准备数据验证
def textParse(bigString):
"""
Function: 切分文本
Args: bigString:输入字符串
Returns: [*]:切分后的字符串列表
"""
import re
#利用正则表达式,来切分句子,其中分隔符是除单词、数字外的任意字符串
listOfTokens = re.split(r'\W*', bigString)
#返回切分后的字符串列表
return [tok.lower() for tok in listOfTokens if len(tok) > 2]
def spamTest():
"""
Function: 贝叶斯垃圾邮件分类器
Args: 无
Returns: float(errorCount)/len(testSet):错误率
vocabList:词汇表
fullText:文档中全部单词
"""
#初始化数据列表
docList = []; classList = []; fullText = []
#导入文本文件
for i in range(1, 26):
#切分文本
wordList = textParse(open('email/spam/%d.txt' % i).read())
#切分后的文本以原始列表形式加入文档列表
docList.append(wordList)
#切分后的文本直接合并到词汇列表
fullText.extend(wordList)
#标签列表更新
classList.append(1)
#切分文本
#print('i = :', i)
wordList = textParse(open('email/ham/%d.txt' % i).read())
#切分后的文本以原始列表形式加入文档列表
docList.append(wordList)
#切分后的文本直接合并到词汇列表
fullText.extend(wordList)
#标签列表更新
classList.append(0)
#创建一个包含所有文档中出现的不重复词的列表
vocabList = createVocabList(docList)
#初始化训练集和测试集列表
trainingSet = list(range(50)); testSet = []
#随机构建测试集,随机选取十个样本作为测试样本,并从训练样本中剔除
for i in range(10):
#随机得到Index
randIndex = int(random.uniform(0, len(trainingSet)))
#将该样本加入测试集中
testSet.append(trainingSet[randIndex])
#同时将该样本从训练集中剔除
del(trainingSet[randIndex])
#初始化训练集数据列表和标签列表
trainMat = []; trainClasses = []
#遍历训练集
for docIndex in trainingSet:
#词表转换到向量,并加入到训练数据列表中
trainMat.append(setOfWords2Vec(vocabList, docList[docIndex]))
#相应的标签也加入训练标签列表中
trainClasses.append(classList[docIndex])
#朴素贝叶斯分类器训练函数
p0V, p1V, pSpam = trainNB0(array(trainMat), array(trainClasses))
#初始化错误计数
errorCount = 0
#遍历测试集进行测试
for docIndex in testSet:
#词表转换到向量
wordVector = setOfWords2Vec(vocabList, docList[docIndex])
#判断分类结果与原标签是否一致
if classifyNB(array(wordVector), p0V, p1V, pSpam) != classList[docIndex]:
#如果不一致则错误计数加1
errorCount += 1
#并且输出出错的文档
print("classification error",docList[docIndex])
#打印输出信息
print('the erroe rate is: ', float(errorCount)/len(testSet))
#返回词汇表和全部单词列表
#return vocabList, fullText5.利用sklearn实现垃圾邮件分类
class sklearn.naive_bayes.MultinomialNB(alpha, fit_prior, class_prior)
MultinomialNB假设特征的先验概率为多项式分布,即如下式:
![]()
其中,P(Xj=xjl|Y=Ck)P(Xj=xjl|Y=Ck)是第k个类别的第j维特征的第l个个取值条件概率。mkmk是训练集中输出为第k类的样本个数。λλ 为一个大于0的常数,常常取为1,即拉普拉斯平滑。也可以取其他值。
参数alpha即为上面的常数λλ,如果你没有特别的需要,用默认的1即可。如果发现拟合的不好,需要调优时,可以选择稍大于1或者稍小于1的数。布尔参数fit_prior表示是否要考虑先验概率,如果是false,则所有的样本类别输出都有相同的类别先验概率。否则可以自己用第三个参数class_prior输入先验概率,或者不输入第三个参数class_prior让MultinomialNB自己从训练集样本来计算先验概率,此时的先验概率为P(Y=Ck)=mk/mP(Y=Ck)=mk/m。其中m为训练集样本总数量,mkmk为输出为第k类别的训练集样本数。总结如下:
| fit_prior | class_prior | 最终先验概率 |
| false | 填或者不填没有意义 | P(Y=Ck)=1/kP(Y=Ck)=1/k |
| true | 不填 | P(Y=Ck)=mk/mP(Y=Ck)=mk/m |
| true | 填 | P(Y=Ck)=P(Y=Ck)=class_prior |
import numpy as np
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
# 预处理数据
def text_parse(big_string):
token_list = big_string.split()
return [tok.lower() for tok in token_list if len(tok)>2]
# 去除列表中重复元素,并以列表形式返回
def create_vocab_list(data_set):
vocab_set = set({})
for d in data_set:
vocab_set = vocab_set | set(d)
return list(vocab_set)
# 统计每一文档(或邮件)在单词表中出现的次数,并以列表形式返回
def words_to_vec(vocab_list, input_set):
return_vec = [0] * len(vocab_list)
for word in input_set:
if word in vocab_list:
return_vec[vocab_list.index(word)] += 1
return return_vec
# 朴素贝叶斯主程序
doc_list, class_list, x = [], [], []
for i in range(1, 26):
# 读取第i篇垃圾文件,并以列表形式返回
word_list = text_parse(open('email/email/spam/{0}.txt'.format(i), encoding='ISO-8859-1').read())
doc_list.append(word_list)
class_list.append(1)
# 读取第i篇非垃圾文件,并以列表形式返回
word_list = text_parse(open('email/email/ham/{0}.txt'.format(i), encoding='ISO-8859-1').read())
doc_list.append(word_list)
class_list.append(0)
# 将数据向量化
vocab_list = create_vocab_list(doc_list)
for word_list in doc_list:
x.append(words_to_vec(vocab_list, word_list))
# 分割数据为训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, class_list, test_size=0.25)
x_train, x_test, y_train, y_test = np.array(x_train), np.array(x_test),\
np.array(y_train), np.array(y_test)
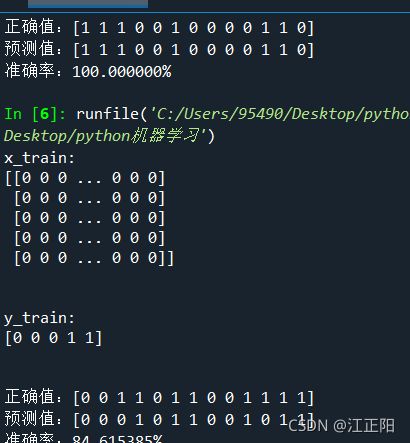
print("x_train: ")
print(x_train[:5])
print("\n")
print("y_train: ")
print(y_train[:5])
print("\n")
# 训练模型
nb_model = MultinomialNB()
nb_model.fit(x_train, y_train)
# 测试模型效果
y_pred = nb_model.predict(x_test)
# 输出预测情况
print("正确值:{0}".format(y_test))
print("预测值:{0}".format(y_pred))
print("准确率:%f%%" % (accuracy_score(y_test, y_pred)*100))