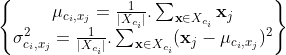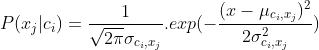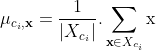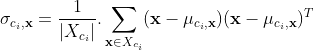朴素贝叶斯（Naive Bayes）详解
朴素贝叶斯是贝叶斯分类器中的一种模型，用已知类别的数据集训练模型，从而实现对未知类别数据的类别判断。其理论基础是贝叶斯决策论（Bayesian decision theory）。
一：基础知识
（1）联合概率：
联合概率表示两个事件共同发生的概率，例如事件A与事件B同时发生，则表示为P(A,B)或P(AB)。
对于上面的八个物体，设事件A为从中取出圆形物体，事件B为从中取出红色物体，则联合概率P(A,B)=0.25。
（2）边缘概率
边缘概率是指某个事件发生的概率，而与其它事件无关，它是由联合概率边缘化得到的，即在联合概率中，把最终结果不需要的事件合并成事件全概率而消失。例如P(A,B1)表示事件A与事件B1同时发生的概率，P(A,B2)表示事件A与事件B2同时发生的概率，若事件B1与B2合在一起为B事件发生的全部情况，则A 的边缘概率P(A)=p(A,B1)+P(A,B2)。
以（1）中的8个物体为例，A表示从中取出圆形物体，B1表示取出红色物体，B2表示取出蓝色，B3表示取出绿色，则A的边缘分布为P(A)=P(A,B1)+P(A,B2)+P(A,B3)=0.25+0.125+0.25=0.625,也就是从中取出圆形物体是概率P(A)=5/8=0.625。
（3）条件概率
条件概率是概率论中的基础知识，由于本文需要大量使用，所以兔兔在这里先回顾一下。条件概率，顾名思义就是在已知一个事件B发生的情况下，此时另一个事件A发生的概率，符号表示为P(A|B)，它等于联合概率P(A,B)除以边缘分布P(B),即：
或可以写成：
表示事件A,B联合概率等于在B发生的条件下A发生的条件概率乘以B事件发生概率。以（1）中的8个物体为例，A事件表示取出圆形物体，B事件表示取出红色物体，则P(A|B)表示从红色物体中取出圆形的概率，数值为2/4=0.5；P(B)表示取出红色的概率，数值为4/8=0.5。所以事件A,B的联合概率为0.5×0.5=0.25，与事实相符。
由于P(A,B)也等于P(B|A)P(A) （P(A,B)与P(B,A)含义相同，数值相等），所以也有公式：
二：贝叶斯决策论
贝叶斯决策论是一种在概率框架下实施决策的方法。它的主要结论是给定某一组数据x，计算在数据为x的条件下，类别为
的概率，即条件概率
（其中i表示所有类别中的第i类）。如果某一类
的条件概率
值最大，则认为该组数据x属于类，即：
其中γ表示所有的可能类别，γ={c1,c2,...cN}。arg 函数是返回使得后面P(c|x)达到最大值的类别c，
称为贝叶斯最优分类器（Bayes optimal classifer)，即根据某组数据x计算该样本属于哪一类。它的推导是基于期望损失（expected loss)、条件风险（condtion risk）R(c|x)、最小化总体风险（或称为“贝叶斯风险”）等方法，由于推导过程比较绕，反而没有上述结论更加直观，所以兔兔在这里就不展开讨论了。
在后面的讲解中，兔兔令训练集为X，它含有n组数据，p个属性（或指标、变量）,每组数据都有相应的类别
，一共有N个类别，属性中的数据可以分为两种情况：一种的连续性的数值数据，如身高、体重、温度等；另一种情况是离散型数据，例如：果蝇眼睛性状中的红眼与白眼、兔子的毛发性状中长毛、短毛、卷毛等。
（1）“判别式模型”与“生成式模型”
“判别式模型”（discriminative models）与生成式模型“（generstive models）的区别在于是否需要学习出联合概率分布P(X,Y)。“判别式模型”是直接建模，并根据某一数据直接预测；“生成式模型”是模型先对联合概率分布P(x,y)建模，能够学习出联合概率分布，然后由贝叶斯公式得出条件分布P(y|x)，进而进行判断。例如神经网络、支持向量机、距离判别法、逻辑回归等都属于判别式模型；混合高斯模型、隐马尔可夫、玻尔兹曼机以及本文的朴素贝叶斯等都属于生成式模型。对于前面讲到的贝叶斯决策，如果直接对P(c|x)建模，直接计算判断x属于哪一类，则是判别式模型，如果先对联合概率分布P(x,c)建模，在由此得到P(c|x)，则是生成式模型。在贝叶斯决策中，主要还是采用生成式模型的方法。根据前面的条件概率公式，可得：
其中P(c)称为类“先验”(prior)概率，P(x|c)称为样本x相对于类c的类条件概率(class-conitional probability，或称为“似然” likelihood)，P(x)为用于归一化的“证据”(evidence)因子。这样，计算P(c|x)问题，就转化成计算P(c)与P(x|c)问题。
（注：对于给定的数据x，由于计算不同类别c下P(c|x)并比较大小，可以发现它们计算式分母都是P(x)，即最终判断结果不受P(x)的影响，而与类别c有关。所以最终我们只需比较P(c).P(x|c)即可。）
所以，在这种情况下，我们只需要利用训练集X求出不同类别的类先验概率P(c)与类条件概率P(x|c)，在之后的预测过程中只需将x代入式中计算并进行比较，从而得出结论。
（2）P(c)计算方法
计算类先验概率，只需用训练集中类ci总数除以样本数据总个数n即可。即：
其中Xci表示类别为ci样本，X为总样本，| |表示样本的个数。
举例：
| 身高(cm) | 体重(kg) | 性别 | 胖瘦类型 | |
| 1 | 181 | 80 | M | 中 |
| 2 | 179 | 50 | W | 瘦 |
| 3 | 155 | 70 | M | 胖 |
| 4 | 168 | 50 | M | 中 |
| 5 | 160 | 40 | W | 瘦 |
对于以上数据，类别为"瘦"的概率为P(瘦)=2/5=0.4，“中”为P(中)=2/5=0.4。
（3）离散型属性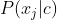
计算方法
我们在这里暂不讨论P(x|c)的情况，而是其中某一属性j的类条件概率。对于离散型数据，其某一属性类条件概率为：在c类数据中中所有值为xj的样本个数除以类别为c的样本个数，即：
其中
表示属于ci类且属性j的取值为xj的样本个数，
表示属于ci类样本。
举例：
对于上面的数据，P(性别=男|瘦)=0/2=0，P(性别=男|中)=2/2=1,P(性别=女|中）=0/2=0。只需先找类别，在该类别内找对应属性值（男or女）,从而求出类条件概率。
（4）连续性属性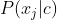计算方法与极大似然法。
对于连续性数值，我们需要知道关于属性j在类别c的条件概率分布形式并估计概率分布中的参数，从而在预测过程中根据给定的xj值计算P(xj|c)。参数的计算主要通过极大似然估计（Maximum Likelihood Estimation,MLE）来进行参数估计（parameter estimation）。
（注：在频率主义学派中，认为概率分布的参数虽然未知，但是值是固定的，而贝叶斯学派认为概率分布的参数不是固定的，其本身也服从一定的分布，而我们在数理统计、多元统计中更多接触的是前者，所以本文也采用频率主义学派的极大似然估计法。并且这里认为分布都是服从正态分布）。
在这种情况下，我们对于属性j，采用极大似然法，利用样本来估计类别ci中属性j服从正态分布的参数
和
的值，兔兔在这里省去推导，最终结论为：
为类别ci数据中属性j数据的方差，
为类别为ci数据中属性j数据的方差，即：
其中表示类别为ci的样本，x为其中的一组数据，xj表示该组数据的第j个属性。根据上述公式计算得出参数，在计算一个属性某一数据x的类条件概率时把该数据与参数代入下式即可。
举例：
以上面数据的身高属性为例，“瘦”类身高均值为μ=(179+160)/2=169.5,方差为[(179-169.5)^2+(160-169.5)^2]/2=90.25，则对于身高160，P(x=160|瘦)=
（5）多个连续性属性的类条件概率
兔兔在前面讲了离散型与连续型某一属性的类条件概率，是为了后面朴素贝叶斯作准备。这里讲述多个连续型属性的类条件概率，在后面朴素贝叶斯中是不会用到的。
对于多个连续型属性情况，我们认为这些连续性属性服从多元正态分布，设连续性属性个数为m，则认为类条件概率P(x|ci)服从m元正态分布(其中x为m维列向量，向量中每一行与属性相对应)。根据多元统计中的参数估计，我们计算得到参数
为类别ci样本中属性1~m的均值向量，
为类别ci样本中属性1~m的协方差阵，即：
其中x为ci类中各属性数据组成的m维列向量。这样对给定的一组数据x，将其与上面参数代入多元正态分布函数中，即可求得此时的P(x|ci)。
![P(\mathbf{x}|c_i)=(2\pi)^{-m/2}.|\sigma_{c_i,\textbf{x}}|^{-1/2}.exp[-\frac{1}{2}(\textbf{x}-\mu_{c_i,\mathbf{\mathbf{}x}})^T \sigma_{c_i,\textbf{x}}^{-1}(\textbf{x}-\mu_{c_i,\mathbf{x}})]](http://img.e-com-net.com/image/info8/130e9031672c4f998986eaf89aba8979.gif){kind=small}
式中|σ|表示协差阵的行列式值，
表示协差阵逆矩阵。
三：朴素贝叶斯
我们在前面贝叶斯决策论中，知道判断未知数据x的类别，在于寻找类别c，使得P(c|x)最大。后来进一步简化为使得P(c).P(x|c)最大的类别c。P(c)的计算较为简便，各个单独属性xj的类条件概率也能够计算，现在问题在于，如何计算多个属性x的P(x|c)？属性中若都是连续型可以采用上面(5)的方法，若都是离散型的、或多个离散型与多个连续性属性呢？
对于这样的问题，朴素贝叶斯认为各个属性是独立的，即“属性条件独立性假设”（attribute conditional independence assumption），假设每个属性都独立地对分类结果产生影响，这也是“朴素”一词的来源。这样联合概率就可以简化为各个属性类条件概率的乘积，即：
如果都是连续性属性的情况，若使用朴素贝叶斯，就认为各属性均服从正态分布且相互独立，即多元正态分布中协差阵对角线以外的元素都为0的情况。
这样，经过训练后，我们根据某一未知类别数据x，计算：
找到使其数值最大的类别即可。
（1）缺陷与改进
我们发现，由于使用P(xi|c)连续相乘，一旦某一属性中某值的类条件概率为0，此时无论其它属性如何，即使在其它属性上明显属于某一类ci，此时结果也是0，这明显是不太合理的（注：这种情况主要发生在离散型属性数据，即待预测数据的某一属性携带的信息被训练集中未出现的属性值抹去）。另一方面，如果属性很多，各个属性的类条件概率值较小，连续相乘后的值会很小，以至于四舍五入后接近于0（注：该情况在两类属性中都会出现，也称为“下溢出”）。所以，我们要对式子进行改进，避免某属性为0对结论的干扰以及连续相乘后值过小的情况，同时也不会影响各个类条件概率的相对大小关系。
对于属性某值类条件概率为0的情况，常采用“拉普拉斯修正”（Laplacian correction）来解决。即：在离散型属性情况下，二(2)公式中分子加1，分母加上样本的可能的类别数N；二（3）的公式中分子中加1，分母加上样本第i个属性可能的取值数Ni。
举例：
以前面的数据为例，P(瘦）=(2+1)/(5+3)=3/8。5表示样本数，3表示“瘦，中，胖”类别数。
P(M|瘦)=(0+1)/(2+2)=1/4。0表示在“瘦”条件下M的个数，2分别表示属于“瘦”样本个数与性别属性的取值数(M与W)。
对于连续相乘导致下溢的情况，可以在计算P(c)与P(x|c)后取对数log，即：用logP(c)与logP(x|c)代替P(c)、P(x|c)。根据对数计算规律，最后计算结果为这些对数相加。
利用上述公式代替前面“三”中的公式，进行最后的计算，便可以避免下溢出问题。
四：实际应用
（1）dry bean dataset 数据集训练与预测
兔兔在这里采用dry bean dataset 数据集进行训练，由于数据集中同类数据都在一起，所以先把数据集打乱，选取9000组数据作为训练集，4000组数据作为测试集。该数据集所有属性都为连续型，没有离散型。但是为了模型的普适性，下面代码可以用于连续型、离散型以及离散与连续型混合数据的朴素贝叶斯分类，使用前将数据初步处理，转化成np.array类型，并拆分成样本与对应的类别标签即可使用。
class NB:
'''朴素贝叶斯分类器'''
def __init__(self,data,label):
self.data=data #训练数据
self.label=label #训练数据类别
self.n=len(data) #数据样本个数
self.p=len(data[0]) #属性个数
self.pCondition,self.pClass=self.train()
def Cal_class(self):
'''计算训练样本的类别'''
c=set()
for i in self.label:
c.add(i)
return c
def Cal_value(self,attr):
'''计算属性attr的可能取值'''
v=set()
for i in self.data[:,attr]:
v.add(i)
return v
def train(self):
'''计算P(c)与P(x|c)'''
str_type=type(np.array(['a'])[0]) #用于后面属性数据类型的判断，此处为numpy.str类型
int_type=type(np.array([1])[0]) #numpy.int类型
float_type=type(np.array([1.1])[0]) #numpy.float类型
c=self.Cal_class()
pClass={} #用于储存各类的概率P（c）
numClass={} #用于储存各类的个数
pCondition=[{} for i in range(self.p)] #列表中每个字典用于储存对应属性的类条件概率；若为连续性，储存μ与σ
for i in range(self.n):
if self.label[i] not in pClass:
pClass[self.label[i]]=1/(self.n+len(c)) #分子加1，为拉普拉斯修正
numClass[self.label[i]]=0
pClass[self.label[i]]+=1/(self.n+len(c))#统计各类出现的概率
numClass[self.label[i]]+=1 #统计各类的数值
for j in range(self.p):
'''逐个属性计算'''
if type(self.data[0][j])==str_type:
'''计算离散型属性的类条件概率'''
v = self.Cal_value(attr=j)
for i in range(self.n):
if self.label[i] not in pCondition[j]:
init_num = [1/(pClass[self.label[i]]+len(v)) for i in range(len(v))] #初始数据，并采用拉普拉斯修正
pCondition[j][self.label[i]]=dict(zip(v,init_num)) #用于统计label[i]类下的j属性的条件概率
pCondition[j][self.label[i]][self.data[i][j]]+=1/(pClass[self.label[i]]+len(v))
elif type(self.data[0][j])==float_type or int_type:
'''计算连续型属性的类条件概率'''
data_class={} #储存该属性中各类对应的数据
for i in range(self.n):
if self.label[i] not in data_class:
data_class[self.label[i]]=[self.data[i][j]]
else:
data_class[self.label[i]].append(self.data[i][j])
for key in data_class.keys():
miu,sigma=np.mean(data_class[key]),np.var(data_class[key])
pCondition[j][key]={'miu':miu,'sigma':sigma}
return pCondition,pClass
def Cal_p(self,attr,x,c):
'''计算属性attr中值为x的c类条件概率：P(x|c)
attr:属性，值为0~p-1
x:值，为连续的数或离散的值
c:类'''
if 'miu' and 'sigma' in self.pCondition[attr][c]:
'''判断是否为连续型属性，此时是连续型属性'''
miu=self.pCondition[attr][c]['miu']
sigma=self.pCondition[attr][c]['sigma']
p=np.exp(-(x-miu)**2/(2*sigma))/np.sqrt(2*np.pi*sigma)
return p
else:
p=self.pCondition[attr][c][x]
return p
def predict(self,x):
'''根据一组数据x预测其属于哪一类
x:长度为p的列表或array类型'''
p={} #储存属于各类的概率
for c in self.pClass.keys():
pc=np.log(self.pClass[c])
for i in range(self.p):
pc+=np.log(self.Cal_p(attr=i,x=x[i],c=c))
p[c]=pc
maxp=max(p.values()) #选取最大概率
for key,value in p.items():
if value==maxp:
return key
def test(self,testData,testLabel):
'''利用测试集测试模型准确性'''
n=len(testData)
correct=0 #统计正确的个数
for i in range(n):
if self.predict(testData[i])==testLabel[i]:
correct+=1
return correct/n
if __name__=='__main__':
df=pd.read_csv('Dry_Bean_Dataset.csv')
df=pd.DataFrame(df)
df=np.array(df)
np.random.shuffle(df)
traindata=df[0:9000,0:-1]
trainlabel=df[0:9000,-1]
testdata=df[9000:13000,0:-1]
testlabel=df[9000:13000,-1]
nb=NB(data=traindata,label=trainlabel)
correct_rate=nb.test(testdata,testlabel)
print(correct_rate)兔兔运行几次，准确率都在90%附近，说明准确率较高。
如果给定某一数据，预测其类别，在训练后把数据x输入到predict函数即可。
nb=NB(data=traindata,label=trainlabel)
c=nb.predict(x=testdata[10])
print(c)
print(testlabel[10])兔兔在训练后随便找样本中一组数据进行预测，得到c为预测类别，testlabel[10]为真实类别，通常情况下，预测还是比较准确的。
（2）文档分类问题
朴素贝叶斯的一个重要应用是文档的自动分类，其基本方法与前面较为相似。对于文档分类问题，我们先从所有文档中提取单词，并把这些词汇以列表形式排列，形成单词表；之后对于每一个文本，先初始长度与词汇表长度相等、且每个元素为0的列表，然后看该对应的单词是否在该文本中出现，出现则对应位置的值为1，即构建文档向量，采用这种方法构建的文档向量不考虑单词出现的频次，相当于假设单词是等权重的，只考虑是否出现该单词，称为词集模型(set of words model)。例如：对于两个文本"it is a rabbit"," I am a rabbit",词汇表可以表示成[it,is,am,I,a,rabbit]，此时第一句就可以表示为[1,1,0,0,1,1]，第二句为[0,0,1,1,1,1]。对于多个文本，仍是如此。该方法属于朴素贝叶斯基于贝努力模型的实现。
另一种是考虑某一文档中单词出现的频次来构建文档向量，即文档向量对应位置数值表示该文档中某单词出现的次数，而不像前面那样仅用0，1表示单词是否出现在文本中。这种方法被称为词袋模型(bag of words model)。该方法属于朴素贝叶斯基于多项式模型的实现。
对于这些文本数据，除了把文档转换成文档向量，还要对每个文档的类别进行人工标注，之后进行训练。
在训练过程中，统计每一类中各个单词的词频，即该类的所有文档中出现某一单词个数与该类文档所有单词之比（可以考虑单词在文档中出现频次或不考虑，即前面的词袋或词集模型)。对应就是前面的类条件概率P(x|c)。P(c)与前面相同，统计各类出现的概率。
由于这里也会出现某单词的类条件概率为0的情况，所以同样需要用拉普拉斯修正，这里采用方法是：构建文档向量时，令初始值都为1，单词总数加2即可。预测分类时，计算条件概率后取对数，再与预测文档向量对应位置元素相乘求和，加上logP(c)。
import numpy as np
class NB:
def __init__(self,data,label):
self.data=data
self.label=label
self.VocaList=self.get_VocaList()
self.p=len(self.VocaList) #单词表长度
self.n=len(data) #样本数据个数
self.pClass,self.pCondition=self.train()
def get_VocaList(self):
VocalList=set()
for i in self.data:
VocalList=VocalList | set(i) #求单词集合并集
return list(VocalList)
def get_WordsVec(self,words):
'''构建文档向量'''
Words_Vec=np.ones(shape=self.p)
for word in words:
if word in self.VocaList:
Words_Vec[self.VocaList.index(word)] +=1 #词袋模型
#Words_Vec[self.VocaList.index(word)] =1 #词集模型
return Words_Vec
def train(self):
pClass={} #各类概率P(c)
numWords={} #各类数据某单词数
pCondition={} #各个单词的类条件概率
for i in range(self.n):
if self.label[i] not in pClass:
pClass[label[i]]=0
numWords[label[i]]=np.zeros(shape=self.p)
pClass[label[i]]+=1/(self.n)
numWords[label[i]]+=self.get_WordsVec(words=self.data[i])
for key in pClass.keys():
pCondition[key]=numWords[key]/(2+np.sum(numWords[key]))
return pClass,pCondition
def predict(self,words):
'''预测文档words属于哪一类'''
v=self.get_WordsVec(words=words)
p={}
for key in self.pClass.keys():
p[key]=np.sum(np.log(self.pCondition[key])*v)+np.log(self.pClass[key])
pmax=max(p.values())
for key,value in p.items():
if value==pmax:
return key
if __name__=='__main__':
txt=['it is a lovely rabbit',
'This Dog is a pet',
'I like singing',
'He is singing',
'The rabbit and dog are pet',
'The song is very nice',
'This mathematical problem is very difficult',
'I like study',
'I like math and can solve mathematical problems very well',
'Have you heard this song']
label=['pet','pet','music','music','pet','music','study','study','study','music']
data=[]
for i in txt:
data.append(i.split())
nb=NB(data=data,label=label)
nb.train()
c=nb.predict(words=['it','is','a','pet'])
c1=nb.predict(words=['I','like','math'])
print(c,c1)最终预测c为pet类，c1为study类，结果较为准确。
总结：
朴素贝叶斯作为一种基于概率的分类方法，其应用是十分广泛的，并且大多数情况下分类预测效果较好，训练速度较快。针对贝叶斯决策问题中P(x|c)不易求解的问题，该方法采用了属性条件独立性假设，但是现实情况下这种假设难以成立，所以针对该问题后面又有了半朴素贝叶斯等方法的出现。