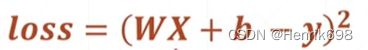PyTorch-02梯度下降Gradient Descent、回归案例、手写数字识别案例
PyTorch-02梯度下降Gradient Descent、回归案例、手写数字识别案例
了解梯度下降
梯度下降是深度学习的精髓。整个deep learning是靠梯度下降所支撑的。可以求解一个非常难的函数,使用的方法就是梯度下降算法。
求一个函数的极小值,就可以先求其函数对应的导数,再检验这个函数的导数是否为极大值或者极小值点。梯度下降与上述的方法类似,但这里还需要一个迭代计算的过程。
例子:
函数y=x^2·sin(x)
该函数导数y’=2·x·sin(x) + x^2·cos(x)
在每获得一个倒数的时候,在x基础上减去y函数在x处的导数。即x’=x-∂x这样就可以获得一个新的x。
比如说,该函数在某一处的x为2.5,其函数y在x为2.5处时的导数为-0.9,新的x=2.5-0.9,但是这里如果之间减去-0.9,会让新的x变化过快,所以这里需要给一个缩放倍数(即学习的速率)使得新x调整的过程不会过大。
所以最终新的 x’ = x - ∂x·learningRate,这样新的x变化情况就可以变化的非常非常小。
假设x=5时,learningRate = 0.005,∂x=0,该函数y有最小值,即x’=5 - 0·0.005 = 5 ,这样x’依然为5,实际上∂x不会是0,会有一定的计算误差,x’会在5附加产生一定的抖动。

梯度下降思想在线性回归情况中的应用:
理想情况:精确求解Closed Form Solution

对于精确求解很多实际情况下是做不到的,但是如果可以达到近似求解并且在实际情况下被证明可行,这样就已经满足我们的目的了,不需要一个非常准确的精确求解Closed Form Solution。
真实情况:伴随着噪声

这里我们需要求解的是y = w·x + b 这个函数,与真实y之间的差值,即wx + b 与y真实值之间的差值和最小。这里表示均方误差最小。loss = (WX+b-y)^2的最小值。使得y真实与wx+b之间更加接近。
案例:

对于具体的方程:loss = ∑i (w·xi+b-yi)^2 要求解w和b,观测到的具体值是xi和yi(xi表示第i个观测到的样本)。借助梯度下降的方法,计算出一个极小值,希望一个wx+b逼近于y,即(y-(wx+b))这个的极小值。在这个取到极小值的时候的w’ 和b’ 的值就是我们需要求解的,即获得最能拟合出真实值y情况的w’x+b’。

loss = (w·xi+b-yi) ^2
∑i (w·xi+b-yi)^2 最小,这个过程是很好理解的:

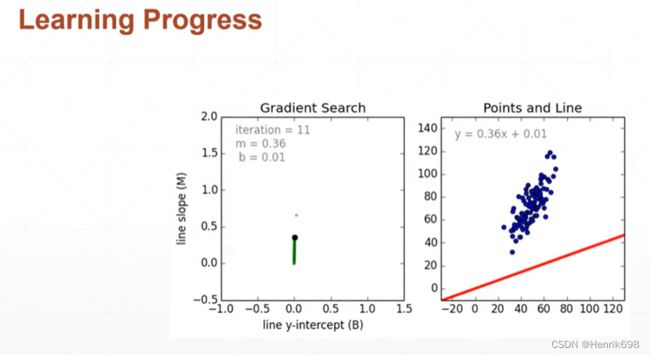
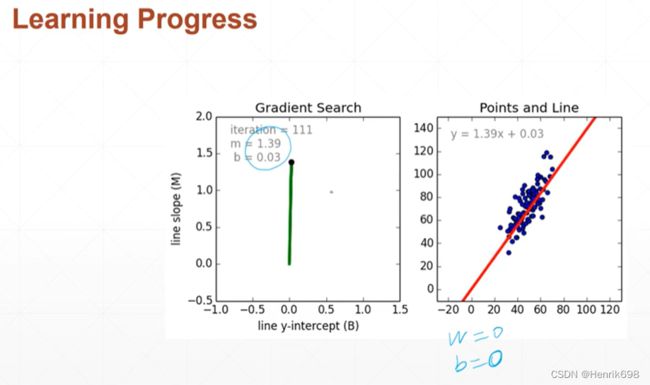
loss是大于等于0的,所以b=0,w=1左右,loss是最小的。如果loss函数能够可视化的话,就可以搜索出loss最低点的w和b的值,就可以很直观的求解出loss最小值。但是现实情况往往不能够可视化,因为x的维度非常非常高,使得w的维度也非常高,因此很难在3维图像上将loss函数曲面图绘制出来。
凸优化Convex optimization
上图是有一个全局最小点的,这样的函数叫做凸函数,会有专门的学科叫凸优化,对于深度学习,我们只需要了解一下即可,不需要深入了解,只需要会使用现成的凸函数优化器即可,即使是非凸函数,也能找到一个局部最小值。
查看一下求解过程:
随机的一个初始点,w=0,b=0为初始点,然后在每一处对w和b来求导,从而不断跟新w值,最终希望有一条直线穿过整个数据集,使得整体的误差偏小。


回归问题实战:
#.csv
32.50234527 31.70700585
53.42680403 68.77759598
61.53035803 62.5623823
47.47563963 71.54663223
59.81320787 87.23092513
55.14218841 78.21151827
52.21179669 79.64197305
39.29956669 59.17148932
48.10504169 75.3312423
52.55001444 71.30087989
45.41973014 55.16567715
54.35163488 82.47884676
44.1640495 62.00892325
58.16847072 75.39287043
56.72720806 81.43619216
48.95588857 60.72360244
44.68719623 82.89250373
60.29732685 97.37989686
45.61864377 48.84715332
38.81681754 56.87721319
66.18981661 83.87856466
65.41605175 118.5912173
47.48120861 57.25181946
41.57564262 51.39174408
51.84518691 75.38065167
59.37082201 74.76556403
57.31000344 95.45505292
63.61556125 95.22936602
46.73761941 79.05240617
50.55676015 83.43207142
52.22399609 63.35879032
35.56783005 41.4128853
42.43647694 76.61734128
58.16454011 96.76956643
57.50444762 74.08413012
45.44053073 66.58814441
61.89622268 77.76848242
33.09383174 50.71958891
36.43600951 62.12457082
37.67565486 60.81024665
44.55560838 52.68298337
43.31828263 58.56982472
50.07314563 82.90598149
43.87061265 61.4247098
62.99748075 115.2441528
32.66904376 45.57058882
40.16689901 54.0840548
53.57507753 87.99445276
33.86421497 52.72549438
64.70713867 93.57611869
38.11982403 80.16627545
44.50253806 65.10171157
40.59953838 65.56230126
41.72067636 65.28088692
51.08863468 73.43464155
55.0780959 71.13972786
41.37772653 79.10282968
62.49469743 86.52053844
49.20388754 84.74269781
41.10268519 59.35885025
41.18201611 61.68403752
50.18638949 69.84760416
52.37844622 86.09829121
50.13548549 59.10883927
33.64470601 69.89968164
39.55790122 44.86249071
56.13038882 85.49806778
57.36205213 95.53668685
60.26921439 70.25193442
35.67809389 52.72173496
31.588117 50.39267014
53.66093226 63.64239878
46.68222865 72.24725107
43.10782022 57.81251298
70.34607562 104.2571016
44.49285588 86.64202032
57.5045333 91.486778
36.93007661 55.23166089
55.80573336 79.55043668
38.95476907 44.84712424
56.9012147 80.20752314
56.86890066 83.14274979
34.3331247 55.72348926
59.04974121 77.63418251
57.78822399 99.05141484
54.28232871 79.12064627
51.0887199 69.58889785
50.28283635 69.51050331
44.21174175 73.68756432
38.00548801 61.36690454
32.94047994 67.17065577
53.69163957 85.66820315
68.76573427 114.8538712
46.2309665 90.12357207
68.31936082 97.91982104
50.03017434 81.53699078
49.23976534 72.11183247
50.03957594 85.23200734
48.14985889 66.22495789
25.12848465 53.45439421
import numpy as np
# y = wx + b
def compute_error_for_line_given_points(b, w, points):
totalError = 0
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
totalError += (y - (w * x + b)) ** 2
return totalError / float(len(points))
def step_gradient(b_current, w_current, points, learningRate):
b_gradient = 0
w_gradient = 0
N = float(len(points))
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
b_gradient += -(2/N) * (y - ((w_current * x) + b_current))
w_gradient += -(2/N) * x * (y - ((w_current * x) + b_current))
new_b = b_current - (learningRate * b_gradient)
new_m = w_current - (learningRate * w_gradient)
return [new_b, new_m]
def gradient_descent_runner(points, starting_b, starting_m, learning_rate, num_iterations):
b = starting_b
m = starting_m
for i in range(num_iterations):
b, m = step_gradient(b, m, np.array(points), learning_rate)
return [b, m]
def run():
points = np.genfromtxt("data.csv", delimiter=",")
learning_rate = 0.0001
initial_b = 0 # initial y-intercept guess
initial_m = 0 # initial slope guess
num_iterations = 1000
print("Starting gradient descent at b = {0}, m = {1}, error = {2}"
.format(initial_b, initial_m,
compute_error_for_line_given_points(initial_b, initial_m, points))
)
print("Running...")
[b, m] = gradient_descent_runner(points, initial_b, initial_m, learning_rate, num_iterations)
print("After {0} iterations b = {1}, m = {2}, error = {3}".
format(num_iterations, b, m,
compute_error_for_line_given_points(b, m, points))
)
if __name__ == '__main__':
run()

可以发现error由最初的5565.107到112.614810。线性回归的拟合的均方误差明显减小了。
手写数字识别问题案例:
MNIST数据集
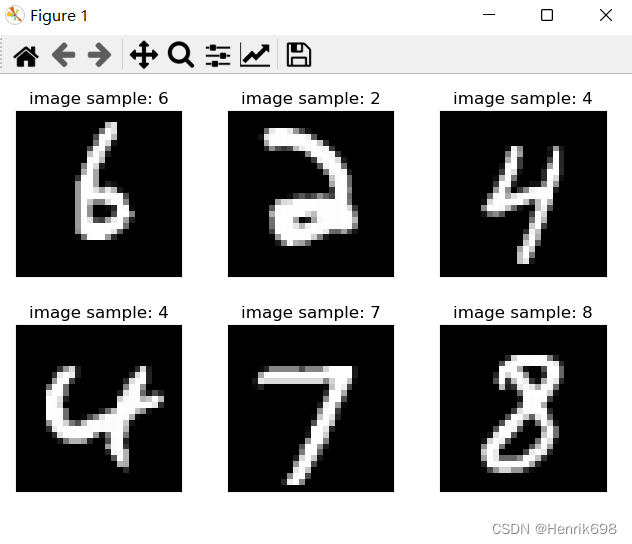
这个数据集每一个数字照片大小是28*28,有7000张。将前6000张做训练集,剩余1000张做测试集。

每一个手写数字图片可以由矩阵来表示,即28行28列,每一个index所对应的值是0到1区间内的值,该值表示灰度值。将这个28行28列的矩阵通过flat操作进行降维,拉伸成1维向量,数据量不变784,这样忽略了位置相关性。在降维后的向量前添加一个维度,使其变为[1,784],这样数据是不变的,只是前面多了一个1。
一个简单的线性模型y=wx+b,但是对于手写数字来说,仅仅使用简单的线性模型是不够的,我们使用三个线性函数的嵌套。

loss损失函数如何计算:
loss = ([预测结果]-[真实值])^2
这里的真实值,需要转换成独热编码one-hot。


对于线性模型很难处理非线性情况,这里引入非线性因子Non-linear Factor。这里非线性因子主要有sigmoid函数(激活函数),ReLU函数等。这里我们选用ReLU函数作为非线性因子。



将上述过程通过python来实现:

最后一层不加relu非线性因子:

主要分为四个步骤对手写数字进行识别:
1、加载图片
2、新建模型
3、训练集
4、测试集

utils.py:
import torch
from matplotlib import pyplot as plt
#绘制下降的曲线:
def plot_curve(data):
fig = plt.figure()
plt.plot(range(len(data)), data, color='blue')
plt.legend(['value'], loc='upper right')
plt.xlabel('step')
plt.ylabel('value')
plt.show()
#绘制图片,识别的结果
def plot_image(img, label, name):
fig = plt.figure()
for i in range(6):
plt.subplot(2, 3, i + 1)
plt.tight_layout()
plt.imshow(img[i][0]*0.3081+0.1307, cmap='gray', interpolation='none')
plt.title("{}: {}".format(name, label[i].item()))
plt.xticks([])
plt.yticks([])
plt.show()
#实现独热编码
def one_hot(label, depth=10):
out = torch.zeros(label.size(0), depth)
idx = torch.LongTensor(label).view(-1, 1)
out.scatter_(dim=1, index=idx, value=1)
return out
mnist_train.py:
import torch
from torch import nn #表示神经网络的一些工作
from torch.nn import functional as F #表示常用的一些函数
from torch import optim #导入优化工具包
#mnist是一个视觉的数据集,所以需要导入torchvision
import torchvision
from matplotlib import pyplot as plt
#导入utils类,即utils.py文件
from utils import plot_image,plot_curve,one_hot
# step1. load dataset
#这里有一个batch_size概念:
#gpu性能非常强大,一次处理1张图片可能需要3毫秒,一次处理多张图片可能也就4到5毫秒。
#这样通过并行处理多张图片,可以大大节省计算时间。
batch_size = 512 #因为图片是28*28的大小,图片比较小,所以这里batch_size就稍微大一些。
#加载训练集
#torch专门加载数据集的方法:
train_loader = torch.utils.data.DataLoader(
#加载mnist数据集
#参数1:指定数据集
#参数2train:指定下载的数据是那60000张训练集数据集,因为有60000张图片是做训练集的,有10000张是测试集的。
#参数3download:表示如果当前文件没有mnist数据集,就从网络上下载下来。
#参数4transform:转换格式,网络下载下来的数据集是numpy格式,需要转换成Tensor格式,该格式是torch的一个数据载体。
#此外还有一个正则化过程normalize,因为神经网络所接受的数据最好均匀分布在0附近,但是我们图片的像素是0到1之间(0的右侧分布),通过减去0.1307再除以标准差这样一个过程使得我们的数据能够在0周围均匀的分布,这样更方便神经网络去优化,这个正则化可以不做,注释掉的话性能会差一些可能70%作用,如果使用正则化效果会好很多80%多。
torchvision.datasets.MNIST('mnist_data', train=True, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
])),
# 参数5batch_size:一次加载多少张图片,并行处理多张图片。
# 参数6shuffle:表示加载的时候随机打散
batch_size=batch_size, shuffle=True)
#加载测试集
test_loader = torch.utils.data.DataLoader(
#这里参数shuffle设置为false,因为测试集就没必要打散了
torchvision.datasets.MNIST('mnist_data/', train=False, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=False)
#将加载的图片显示出来
#next() 返回迭代器的下一个项目。
#next() 函数要和生成迭代器的 iter() 函数一起使用。
#iter() 函数用来生成迭代器,iter(object[, sentinel]),object -- 支持迭代的集合对象。
#sentinel -- 如果传递了第二个参数,则参数 object 必须是一个可调用的对象(如,函数),此时,iter 创建了一个迭代器对象,每次调用这个迭代器对象的__next__()方法时,都会调用 object。
x,y = next(iter(train_loader))
#512张图片,1个通道,28行,28列,label有512个,最小值-0.4242,最大值2.8215,说明在0周围分布。
print(train_loader)
print(x.shape,y.shape,x.min(),x.max())
# print(x)
plot_image(x,y,'image sample')
#step2.create net
class Net(nn.Module):
def __init__(self):
super(Net,self).__init__()
#xw+b
self.fc1 = nn.Linear(28*28,256)
self.fc2 = nn.Linear(256,64)
self.fc3 = nn.Linear(64,10)
def forward(self,x):
# x:[b,1,28,28]
# h1 = xw+b
x = F.relu(self.fc1(x))
# h2 = relu(h1w2+b2)
x = F.relu(self.fc2(x))
# h3 = h2w3+b3
x=self.fc3(x)
return x
net = Net()
#[w1,b1,w2,b2,w3,b3]
optimizer = optim.SGD(net.parameters(),lr=0.01,momentum=0.9)
#step.3 trainning
train_loss = []
for epoch in range(3):
for batch_idx,(x,y) in enumerate(train_loader):
# x: [b,1,28,28],y:[512]
# [b,1,28,28] => [b , feature]
x= x.view(x.size(0),28*28)
# => [b,10]
out = net(x)
#[b,10]
y_onehot = one_hot(y)
#loss = mse(out , y_onehot)
loss = F.mse_loss(out,y_onehot)
optimizer.zero_grad()
loss.backward()
#w' = w - lr*grad
optimizer.step()
train_loss.append(loss.item())
if batch_idx % 10 ==0:
print(epoch,batch_idx,loss.item())
plot_curve(train_loss)
#we get optimal [w1,b1,w2,b2,w3,b3]
#step.4 accuracy
total_correct = 0
for x,y in test_loader:
x = x.view(x.size(0),28*28)
out = net(x)
#out :[b,10] => pred:[b]
pred = out.argmax(dim = 1)
correct = pred.eq(y).sum().float().item()
total_correct += correct
total_num = len(test_loader.dataset)
acc = total_correct/total_num
print('test acc:',acc)
#step.5
x,y = next(iter(test_loader))
out = net(x.view(x.size(0),28*28))
pred = out.argmax(dim =1)
plot_image(x,pred,'test')