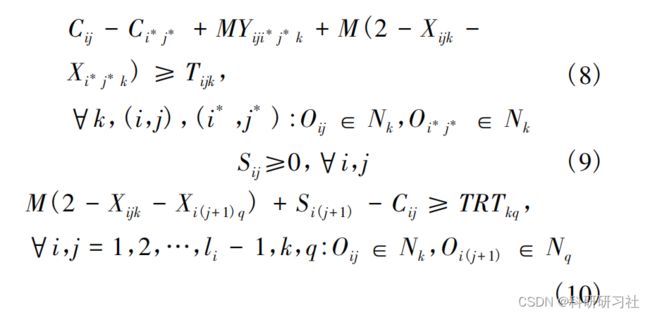【车间调度】基于遗传算法的柔性车间调度（Matlab代码实现）

目录

1 概述

2 模型表示

3 运行结果

4 Matlab代码实现 

5 结论

6 参考文献

7 写在最后

---

1 概述

柔性作业车间调度问题（ flexible job shopscheduling problem,FJSP)是JSP的扩展，以往的JSP和FJSP研究中,大都忽略了运输时间。由于考虑运输时间会使调度优化结果更符合实际,所以考虑运输时间的FJSP研究日益增多10-1,但这些研究并没有考虑运输时间对能耗的影响。FJSP中各工序有多台机床可供选择,造成相邻工序间运输路线存在多种可能，从而使得运输时间不同。若工件运输目的机床处于待机状态,缩短运输时间显然有助于减少其待机能耗。
 

2 模型表示

 

约束条件式(5)表示每道工序只能选择一台机床加工;式(6)表示每道工序的加工起止时间间隔为该工序在选择机床上的加工时间;式(7)和(8)表示若两道工序分属于不同工件,当其在同一机床上加工时,它们的加工时间不允许重叠;式(9)表示任一工序的加工开始时间都是非负的;式(10)表示属于同一工件的工序有先后顺序约束,且各工序的开始时间受运输时间约束。详细讲解见第4部分。

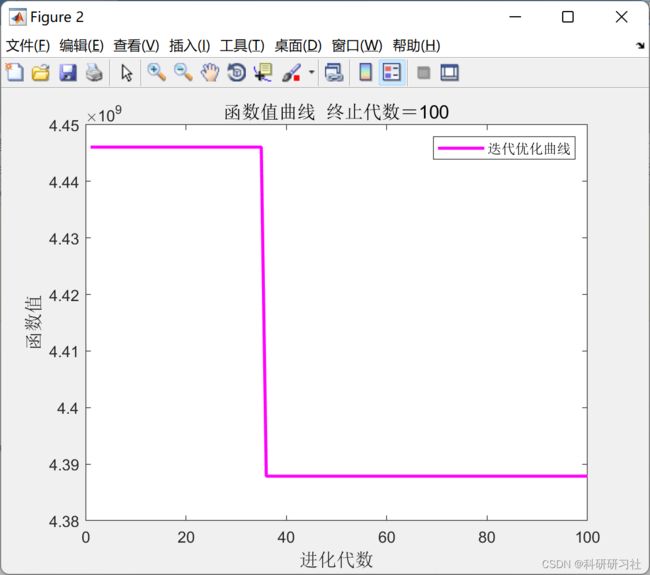
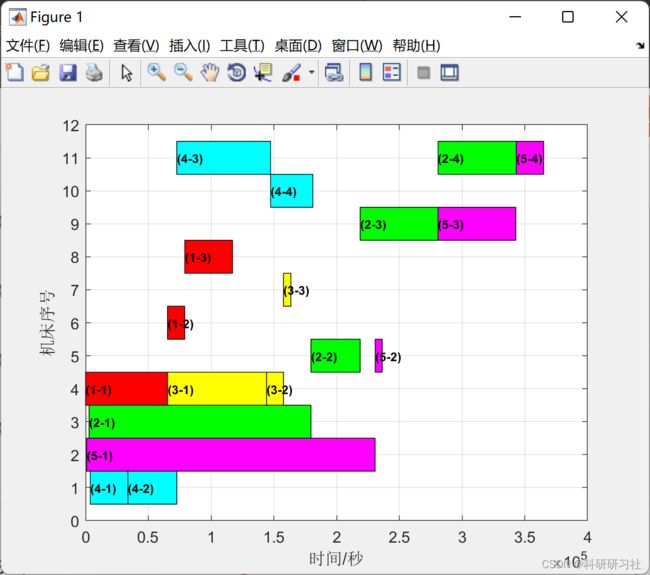
3 运行结果

 

 

4 Matlab代码实现 

本文仅展现部分代码，全部代码及详细文章点击链接：

基于改进遗传算法的柔性车间调度（Matlab代码实现）

function [y,release_time,T_start,T_need,T_end,T_total,T_jiagong,T_duidao,T_kongxian,P_total,P_jiagong,P_duidao,P_kongxian] = fun(x)
nVar = numel(x);
global Global info

%% 从头到尾安排工件进行加工
T_jiagong = 0;
T_duidao = 0;
T_kongxian = 0;
T_start = zeros(Global.I,4); %开工时间
T_need = zeros(Global.I,4); %加工时间
T_end = zeros(Global.I,4); %完工时间
release_time = zeros(1,Global.M); %下一次的可用时间

P_jiagong = 0;
P_duidao = 0;
P_kongxian = 0;

count_gongxu=ones(1,Global.I);
count_gongjian=zeros(1,Global.M); %记录机器使用次数
for i=1:nVar/2
    cur_gongjian = x(i);
    cur_gongxu = count_gongxu(cur_gongjian);
    count_gongxu(cur_gongjian) = count_gongxu(cur_gongjian)+1;
    cur_machine = x(nVar/2+i);
    cur_machine_code = info(cur_gongjian).gongxu(cur_gongxu).bianhao(cur_machine);
    count_gongjian(cur_machine_code) = count_gongjian(cur_machine_code) + 1;
    
    if cur_gongxu==1 %当前工件的首个工序
        if release_time(cur_machine_code)>Global.Ai(cur_gongjian) %当前几床被占用
            T_start(cur_gongjian,cur_gongxu) = release_time(cur_machine_code);
            T_need(cur_gongjian,cur_gongxu) = Global.Ni(cur_gongjian)*sum(info(cur_gongjian).gongxu(cur_gongxu).data(cur_machine,2)) ...
                + info(cur_gongjian).gongxu(cur_gongxu).data(cur_machine,3);
            release_time(cur_machine_code) = release_time(cur_machine_code) + T_need(cur_gongjian,cur_gongxu);
        else %当前机床没有被占用
            T_start(cur_gongjian,cur_gongxu) = Global.Ai(cur_gongjian);
            T_need(cur_gongjian,cur_gongxu) = Global.Ni(cur_gongjian)*sum(info(cur_gongjian).gongxu(cur_gongxu).data(cur_machine,2))  ...
                + info(cur_gongjian).gongxu(cur_gongxu).data(cur_machine,3);
            P_kongxian = P_kongxian + (T_start(cur_gongjian,cur_gongxu)-release_time(cur_machine_code))*Global.m_power(cur_machine,1);
            T_kongxian = T_kongxian+(T_start(cur_gongjian,cur_gongxu)-release_time(cur_machine_code));
            release_time(cur_machine_code) = T_start(cur_gongjian,cur_gongxu) + T_need(cur_gongjian,cur_gongxu);
        end
        T_jiagong = T_jiagong+Global.Ni(cur_gongjian)*sum(info(cur_gongjian).gongxu(cur_gongxu).data(cur_machine,2));
        T_duidao = T_duidao+Global.Ni(cur_gongjian)*sum(info(cur_gongjian).gongxu(cur_gongxu).data(cur_machine,3));
        P_jiagong = P_jiagong + info(cur_gongjian).gongxu(cur_gongxu).data(cur_machine,1)*Global.Ni(cur_gongjian);
        P_duidao = P_duidao + info(cur_gongjian).gongxu(cur_gongxu).data(cur_machine,3)* ...
            Global.m_power(cur_machine_code,2)*Global.Ni(cur_gongjian);
        T_end(cur_gongjian,cur_gongxu) = T_start(cur_gongjian,cur_gongxu) + T_need(cur_gongjian,cur_gongxu);
        
    else %不是首个工序
        if release_time(cur_machine_code)>T_end(cur_gongjian,cur_gongxu-1) %当前几床被占用
            T_start(cur_gongjian,cur_gongxu) = release_time(cur_machine_code);
            T_need(cur_gongjian,cur_gongxu) = Global.Ni(cur_gongjian)*sum(info(cur_gongjian).gongxu(cur_gongxu).data(cur_machine,2)) ...
                + info(cur_gongjian).gongxu(cur_gongxu).data(cur_machine,3);
            release_time(cur_machine_code) = release_time(cur_machine_code) + T_need(cur_gongjian,cur_gongxu);
        else
            T_start(cur_gongjian,cur_gongxu) = T_end(cur_gongjian,cur_gongxu-1);
            T_need(cur_gongjian,cur_gongxu) = Global.Ni(cur_gongjian)*sum(info(cur_gongjian).gongxu(cur_gongxu).data(cur_machine,2)) ...
                + info(cur_gongjian).gongxu(cur_gongxu).data(cur_machine,3);
            P_kongxian = P_kongxian + (T_start(cur_gongjian,cur_gongxu)-release_time(cur_machine_code))*Global.m_power(cur_machine,1);
            T_kongxian = T_kongxian+(T_start(cur_gongjian,cur_gongxu)-release_time(cur_machine_code));
            release_time(cur_machine_code) = T_start(cur_gongjian,cur_gongxu) + T_need(cur_gongjian,cur_gongxu);
        end
        T_jiagong = T_jiagong+T_need(cur_gongjian,cur_gongxu);
        P_jiagong = P_jiagong + info(cur_gongjian).gongxu(cur_gongxu).data(cur_machine,1)*Global.Ni(cur_gongjian);
        T_end(cur_gongjian,cur_gongxu) = T_start(cur_gongjian,cur_gongxu) + T_need(cur_gongjian,cur_gongxu);
    end
end

non_use = Global.M-numel(find(count_gongjian)==0);

T_total = max(release_time);
P_total = P_jiagong + P_duidao + P_kongxian;
xishu = Global.xishu;
y = sum([0.1*T_total P_total].*xishu) + non_use*1000000000;

5 结论

本文针对柔性作业车间的节能运行需求，建立了考虑运输时间的EFJSP模型﹐并利用遗传算法对其求解。所建立的EFJSP模型实际也反映了通过机床选择和工序排序实现车间制造节能运行的方法。案例研究表明该方法具有较好的节能效果,通过合理选择加工机床可减少机床加工时间段的总能耗，而通过优化工序加工顺序可减少机床的待机能耗。后续研究拟考虑随机不确定事件(如机床故障﹐新工件到达)对生产过程能耗的影响,并提高智能算法求解效率。

6 参考文献

[1]何院生. 考虑能耗优化的柔性作业车间动态调度方法研究[D].哈尔滨工业大学,2016.

[2]张中伟,吴立辉,贾顺.柔性作业车间能耗优化研究[J].制造技术与机床,2019(04):162-168.DOI:10.19287/j.cnki.1005-2402.2019.04.032.

7 写在最后

部分理论引用网络文献，如有侵权请联系删除。