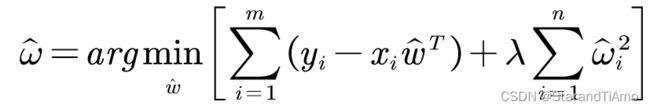机器学习实战（八）——预测数值型数据：回归

机器学习实战（八）——预测数值型数据：回归

一、用线性回归找到最佳拟合曲线

1、线性回归与非线性回归

线性回归：具体是可以将输入项分别乘上一些常量，然后再进行求和得到输出

非线性回归：输入项之间不只是相加的关系，还有更多的形式

2、最小二乘法求回归系数

对于给定的输入数据矩阵$X$，要求解回归系数向量$\omega$，常用的方法是使得误差最小化来求解即：

这里上边的小帽子代表估计值。具体使用numpy实现为：

from numpy import *


def loadDataSet(fileName):
    numFeat = len(open(fileName).readlines()[0].split('\t'))
    # 读取总共有多少个列，包括最后一列的类别
    dataMat = []
    labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numFeat - 1):
            # 最后一个是类别，不考虑
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))

    return dataMat, labelMat


def standRegres(xArr, yArr):
    xMat = mat(xArr)
    yMat = mat(yArr).T  # 因为传进来的label是1*m,转置为m*1
    xTx = xMat.T * xMat  # n*m×m*n，就是n*n的方阵
    if linalg.det(xTx) == 0.0:  # 矩阵的行列式等于0说明该矩阵不可逆
        print("This matrix is singular, cannot do inverse")
        return
    ws = xTx.I * (xMat.T * yMat)
    return ws

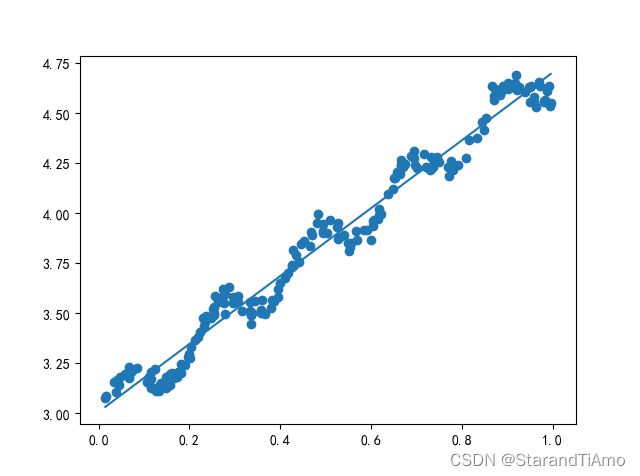
再进行绘图：

fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0])
xCopy = xMat.copy()
xCopy.sort(0)
yHat = xCopy*ws
ax.plot(xCopy[:,1],yHat)
plt.show()

解释一下该行代码：

ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0])

其中主要的是函数flatten()，其函数意义就是对array或者matrix类型的数据结构进行降维

将xMat[:,1]和xMat[:,1].flatten()打印出来可知为：

[[0.067732]
	....
 [0.116163]]
[[0.067732 0.42781  0.995731 0.738336 0.981083 0.526171 0.378887 0.033859
			....
  0.255212 0.730546 0.493829 0.257017 0.833735 0.070095 0.52707  0.116163]]

即将数据从m维降到了1维度，然后在通过.A转成array类型，因为matrix类型不能直接索引，结果就是取出来一个向量进行绘图

二、局部加权线性回归

线性回归容易出现欠拟合现象，可以理解为对全部数据都是权重一样的进行了学习，那么容易受到一些偏离线性程度大的点的影响，便出现拟合效果不佳的现象。而局部加权线性回归的思想是：样本距离待预测的点越近，那么该样本的权重就越大，使得在待预测的点附近能够有更好的线性。

那么此时回归系数的形式为：

这样对角矩阵$W$就构建完成，其对角线的元素$W(i,i)$即为第$i$个样本点对应的权重。并且若样本点距离待预测的点越近，则其权重越大。而高斯核中我们需要自定义的参数为$k$，它决定了在待预测的点附近权重是如何分布的，具体如下：

具体实现代码如下：

def lwlr(testPoint, xArr, yArr, k=1.0):
    xMat = mat(xArr)
    yMat = mat(yArr).T
    m = shape(xMat)[0]
    weights = mat(eye((m)))  # 创建对角矩阵
    for j in range(m):
        diffMat = testPoint - xMat[j,:]  # 对应元素相减
        weights[j,j] = exp(diffMat * diffMat.T/(-2.0 * k**2))  # 计算权重
    xTx = xMat.T * (weights * xMat)
    if linalg.det(xTx) == 0.0:
        print("This matrx is singular, cannot do inverse")
        return
    ws = xTx.I * (xMat.T * (weights * yMat))
    return testPoint * ws

def lwlrTest(testArr,xArr,yArr,k = 1.0):
    m = shape(testArr)[0]
    yHat = zeros(m)  # 这是对原始样本的每一个样本点的y值的重新预测
    for i in range(m):
        yHat[i] = lwlr(testArr[i],xArr,yArr,k)
    return yHat

然后利用绘图来形象化地看出k取值的不同，拟合出的曲线有何区别

解释一下代码：

srtInd = xMat[:,1].argsort(0)
xSort = xMat[srtInd][:,0,:]

第一行代码是根据xMat的第一列进行排序，然后将排序后每一个元素的正确位置形成一个$(m,1)$的矩阵返回到$srtInd$中，然后$xMat[srtInd]$是按照$strInd$中的顺序去索引xMat中的元素，返回的是$(m,1,2)$维度的矩阵，那么就可以通过$[:,0,:]$进行索引，返回一个$(m,1)$的矩阵

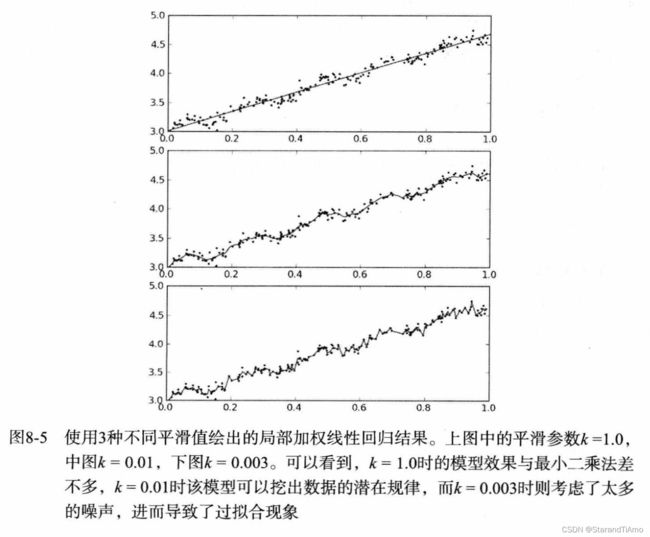
从图中可以看到：

• 当$k=1.0$时相当于权重都差不多，那么跟最小二乘法拟合出来的曲线很相似
• 当$k=0.01$,拟合的效果很好
• 当$k=0.003$时对于待预测点附近的样本点分配的权重过大，导致其他样本没什么贡献，失去了整体性，可以理解为过拟合，对样本数据过度学习导致失去了对未知数据的拟合能力

三、示例：预测鲍鱼的年龄

加入以下代码：

# 用于计算预测值与真实值之间的误差
def rssError(yArr,yHatArr):
    return ((yArr - yHatArr) ** 2).sum()
    
abX,abY = Regression.loadDataSet("abalone.txt")
yHat01 = Regression.lwlrTest(abX[0:99],abX[0:99],abY[0:99],0.1)
yHat1 = Regression.lwlrTest(abX[0:99],abX[0:99],abY[0:99],1)
yHat10 = Regression.lwlrTest(abX[0:99],abX[0:99],abY[0:99],10)
print(Regression.rssError(abY[0:99],yHat01.T))
print(Regression.rssError(abY[0:99],yHat1.T))
print(Regression.rssError(abY[0:99],yHat10.T))

得到结果为：

56.8118936813369
429.89056187020685
549.1181708824906

但这并不能说明选择更小的k值能够取得更好的结果，反而可能是发生了过拟合，因此可以在未知数据上进行测试：

yHat_01 = Regression.lwlrTest(abX[100:199],abX[0:99],abY[0:99],0.1)
yHat_1 = Regression.lwlrTest(abX[100:199],abX[0:99],abY[0:99],1)
yHat_10 = Regression.lwlrTest(abX[100:199],abX[0:99],abY[0:99],10)
print(Regression.rssError(abY[100:199],yHat_01.T))
print(Regression.rssError(abY[100:199],yHat_1.T))
print(Regression.rssError(abY[100:199],yHat_10.T))

运行结果为：

94927.34165777494
573.5261441896996
517.5711905384079

在已知样本集上拟合效果最佳的取值$k=0.1$，在未知样本上的表现很差，反而是在已知样本上效果不好的$k=10$在未知样本上的效果最好。这就说明必须比较各个模型对未知数据的泛化能力才可以说明模型的好坏

局部加权线性回归的缺点在于每次都必须在整个数据集上运行

四、缩减系数来“理解”数据

上述两种方式都存在一种问题，就是当数据的特征数目比样本数目还多，此时将会出现$X^{T}X$不可逆的情况，那么就无法继续计算。解决此问题有以下两种方式

4.1 岭回归

简单地说，岭回归的误差函数加入了惩罚项（类似于正则化），即：

而也就相当于在矩阵$X^{T}X$上加入一个$\lambda$$I$,从而使矩阵可以求逆，那么回归系数的计算公式就变成：

这样可以限制回归系数的和，从而减少不重要的参数的权重，就称为缩减

训练的方法为：在数据集中抽取一部分作为训练集，一部分作为测试，用训练集训练不同$\lambda$对应的模型，得到各自的回归向量后再在测试集上比较不同$\lambda$的好坏，从而选择最好的$\lambda$

训练代码实现为：

def ridgeRegres(xMat, yMat, lam=0.2):
    xTx = xMat.T * xMat  # 维度为n*n
    denom = xTx + eye(shape(xMat)[1]) * lam  # 建立一个n*n的单位矩阵
    if linalg.det(denom) == 0.0:  # 防止lambda为0
        print("This matrix is singular, cannot do inverse")
        return
    ws = denom.I * (xMat.T * yMat)
    return ws


def ridgeTest(xArr, yArr):
    xMat = mat(xArr)
    yMat = mat(yArr).T
    yMean = mean(yMat, 0)  # 对yMat的每一列求均值，返回1*1
    yMat = yMat - yMean
    xMeans = mean(xMat, 0)  # 对每一列求均值，返回1*n
    xVar = var(xMat, 0)  # 对每一列求方差，返回1*n
    xMat = (xMat - xMeans) / xVar  # 对数据进行标准化
    numTestPts = 30  # 这是要训练的lambda的个数
    wMat = zeros((numTestPts,shape(xMat)[1]))
    for i in range(numTestPts):
        ws = ridgeRegres(xMat,yMat,exp(i-10))  # 通过exp(i-10)来选取不同的lambda
        wMat[i,:] = ws.T
    return wMat

可以在鲍鱼的数据集上训练查看$\lambda$变化时各个参数的变化情况：

abX,abY = Regression.loadDataSet("abalone.txt")
ridgeWeight = Regression.ridgeTest(abX,abY)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(ridgeWeight)
plt.show()

其中每一条曲线分别代表每一个${\omega }_i$随着$\lambda$增大时的变化情况，可以看到曲线最终都变成了0，因为后面惩罚项的$\lambda$较大，惩罚力度大。

4.2 lasso

lasso回归与岭回归类似，其误差函数可写成：

它们主要的区别在于：在$\lambda$足够小的时候，lasso回归可以将它认为的一些不重要的特征对应的权重直接变为0；而岭回归虽然也能够压缩不重要变量的权重，但是无法压缩到0

并且lasso回归由于绝对值的限制，无法进行求导来求解$\omega$，因此只能通过其他求取的方法。

4.3 前向逐步回归

前向逐步回归算法可以得到与lasso回归类似的效果，但求解方法更简单。实际上采用贪心算法的思想，伪代码实现为：

数据标准化
外层循环（根据迭代次数）
	设置当前最小误差为正无穷
	内层循环（循环每一个特征）
		增大或者减小该特征
			改变某一个特征的权重得到新的特征向量
			计算新特征向量下的误差
			如果小于当前最小误差就设置最好向量为当前向量

具体的代码实现为：

def stageWise(xArr, yArr, eps=0.01, numIt=100):
    xMat = mat(xArr)
    yMat = mat(yArr).T
    yMean = mean(yMat, 0)  # 对yMat的每一列求均值，返回1*1
    yMat = yMat - yMean
    xMeans = mean(xMat, 0)  # 对每一列求均值，返回1*n
    xVar = var(xMat, 0)  # 对每一列求方差，返回1*n
    xMat = (xMat - xMeans) / xVar  # 对数据进行标准化
    m,n = shape(xMat)
    returnMat = zeros((numIt,n))  # 用来记录ws的变化过程
    ws = zeros((n,1))
    wsTest = ws.copy()
    wsMax = ws.copy()
    for i in range(numIt):
        print(ws.T)
        lowestError = inf  # 初始化最小误差
        for j in range(n):
            for sign in [-1,1]:  # 代表增大或者减小
                wsTest = ws.copy()
                wsTest[j] += eps * sign
                yTest = xMat * wsTest
                rssE = rssError(yMat.A,yTest.A)
                if rssE < lowestError:
                    lowestError = rssE
                    wsMax = wsTest
        ws = wsMax.copy()
        returnMat[i,:] = ws.T
    return returnMat

六、示例：预测乐高玩具套装的价格

6.1、收集数据

原文中访问google的方式已经无法实现，可根据网上各种方式进行实现，这里便不放其他大佬的代码了。

6.2、训练算法：建立模型

数据的特征为： 出品年份、部件数目、是否全新、原价、售价（二手交易）。

先增加一个常数项：

lgX = []
lgY = []
Regression.setDataCollect(lgX, lgY)
lgX1 = mat(ones((shape(lgX)[0],shape(lgX)[1]+1)))
lgX1[:,1:shape(lgX)[1]+1] = mat(lgX)  # 增加一份常数项

接下来为训练的代码：

def crossValidation(xArr,yArr,numVal = 10):
    m = len(yArr)
    indexList = list(range(m))
    errorMat = zeros((numVal,30))
    for i in range(numVal):
        trainX = []
        trainY = []
        testX = []
        testY = []
        random.shuffle(indexList)  # 将该list的顺序打乱
        for j in range(m):
            if j < m*0.9:  # 构建训练集
                trainX.append(xArr[indexList[j]])
                trainY.append(yArr[indexList[j]])
            else:  # 构建测试集
                testX.append(xArr[indexList[j]])
                testY.append(yArr[indexList[j]])
        wMat = ridgeTest(trainX,trainY)  # 采用岭回归
        for k in range(30):
            matTestX = mat(testX)
            matTrainX = mat(trainX)
            meanTrain = mean(matTrainX,0)
            varTrain = var(matTrainX,0)
            matTestX = (matTestX - meanTrain) / varTrain
            yEst = matTestX * mat(wMat[k,:]).T + mean(trainY)
            errorMat[i,k] = rssError(yEst.T.A,array(testY))
            # 这里用train的均值和方差去对test进行标准化，因此在刚才回归得到的权值向量，也是
            # 由训练集的均值和方差去标准化数据的，因此要做到统一
            # 同时预测的Y也要加上训练集的Y的平均值
    meanErrors = mean(errorMat,0)
    minMean = float(min(meanErrors))
    bestWeight = wMat[nonzero(meanErrors == minMean)]  # 找到最佳回归系数
    # 这里直接按照最后一次的wMat去取那个lambda最好的那个
    xMat = mat(xArr)
    yMat = mat(yArr).T
    meanX = mean(xMat,0)
    varX = mean(xMat,0)
    unReg = bestWeight / varX
    print("The best model from Ridge Regression is :\n",unReg)
    print("with constant term:",-1*sum(multiply(meanX,unReg))+mean(yMat))