组合总和
前言
在上篇文章通过组合问题看透回溯法当中我们通过介绍一个组合问题,仔细地分析了组合问题的回溯过程。我们之后会继续介绍一些比较经典的回溯算法题,帮助深入彻底理解回溯算法的执行过程和原理,如果对回溯的整个过程还不是很了解的话可以先阅读上面那篇文章。
组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
例1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。例2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]解法
根据题目的意思我们是需要从给定的集合当中选出几个数据,而且可以进行重复选取,只需要保证被我们选中的数据的和为target即可。对于这个问题我们可以构造一个如下图所示的解树:(下面的树的target = 8, candidates = [2,3,5],当被选中的数据的和大于8的时候我们不需要再往下进行遍历了,因为再选择数据的话,被选择的数据的和只会大于8,这永远不可能等于target = 8)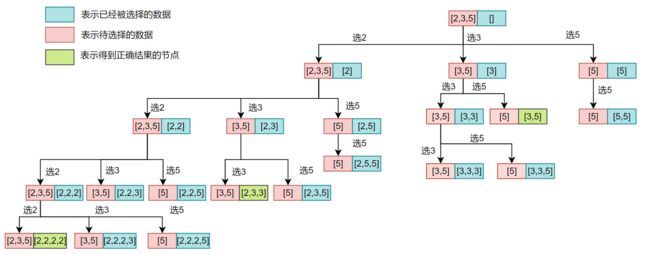
可能你会对上面的解树有所疑问,为什么我们选完2之后是从[2, 3, 5]当中继续选择数据,选择完3之后是从[3,5]当中继续选择数据,而选择完5之后只能从[5]当中选择数据呢?
事实上我们是需要穷举所有的组合的然后一一进行匹配,所以我们现在的问题是上面的树穷举完所有的组合了吗?上面的树是穷举完所有的组合了的,下面我们分析一下为什么上面的树能够覆盖所有的组合。
穷举的组合如下:
- 第一个数据和其他所有数据进行组合,
- 第二个数据和其他所有数据的组合。
- 第三个数据和其他所有数据的组合。
- ....
我们现在来仔细分析一样上面的解树:
- 我们再进行第一次选择的时候,当我们选择完2之后还可以从
[2, 3, 5]当中进行选择,这就表示了2和其他所有数据[3, 5]进行了组合,因为题目说明我们还可以进行重复选择,因此还加入了2,这就保证了2进行了所有的组合。 - 我们再进行第一次选择的时候。当我们选择3的时候,还能从
[3, 5]当中进行选择,选择3的原因也是因为可以重复进行选择,但是选择5的原因是因为需要和其他所有数据进行组合。在这里你可能还会有一个疑问就是3不是只和5进行了组合吗,还缺它和2的组合啊,仔细想一想我们在前一步选择2的时候已经将2和3的组合遍历过一遍了,因此在这不需要再进行组合了。 - 同样的道理我们在第一次选择5的时候,不需要和在他前面的数据进行组合,因为在他前面的数据已经遍历过所有跟5的组合了。
写代码的流程
- 仔细分析程序递归的过程,分析求解问题的树,得到代码的主题思路,根据分析的结果我们可以设计我们函数会有哪些参数,在这道题目当中我们需要记录选中的数据的集合的和,这样就可以避免反复去计算选中数据的和了,还有当前遍历到数据的下标。
backtrace(vector &candidates, int target, int idx, int curSum) 确定递归函数的出口:
- 在这里我们一个出口就是,当被选中的集合当中的数据的和满足要求的时候就进行退出。
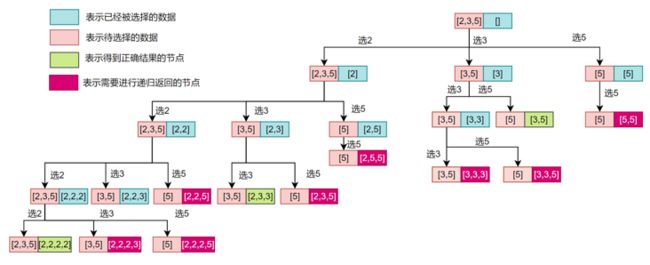
- 当被选中的数据的和大于给定的值的时候我们不需要再进行遍历了,因为即使遍历得到的结果使用会大于给定的值,因此没有遍历的必要了,下图当中深红色的节点就是表示和大于给定的值的情况。
if(curSum == target) {
ans.push_back(path);
}
if(curSum >= target || idx >= candidates.size())
return;根据我们思路确定我们函数的主体部分:
for (int i = idx; i < candidates.size(); ++i) { path.push_back(candidates[i]); curSum += candidates[i]; backtrace(candidates, target, i, curSum); path.pop_back(); curSum -= candidates[i]; }
完整代码
C++版
class Solution {
vector> ans;
vector path;
public:
vector> combinationSum(vector& candidates, int target) {
backtrace(candidates, target, 0, 0);
return ans;
}
void backtrace(vector &candidates, int target, int idx, int curSum) {
if(curSum == target) {
ans.push_back(path);
}
if(curSum >= target || idx >= candidates.size())
return;
for (int i = idx; i < candidates.size(); ++i) {
path.push_back(candidates[i]);
curSum += candidates[i];
backtrace(candidates, target, i, curSum);
path.pop_back();
curSum -= candidates[i];
}
}
};
Java版
class Solution {
private List> res = new ArrayList<>();
private List path = new ArrayList<>();
public List> combinationSum(int[] candidates, int target) {
solve(candidates, target, 0, 0);
return res;
}
public void solve(int[] candidates, int target, int startPosition,
int curSum) {
if (curSum == target) {
res.add(new ArrayList<>(path));
return;
}
else if (curSum > target) return;
for (int i = startPosition; i < candidates.length; i++) {
path.add(candidates[i]);
curSum += candidates[i];
solve(candidates, target, i, curSum);
path.remove(path.size() - 1);
curSum -= candidates[i];
}
}
} 总结
这道题目体现了经典的回溯过程,就是在往集合当加入数据之后,再经过遍历完成,就需要将之前加入的数据移出,而这个回到开始的状态的现象就叫做回溯,即回到之前的状态。但是在这个题目当中还需要注意一点的是他的数据可以重复进行使用,因此在遍历传递参数的时候需要传递的是i而不是i+1,这一点需要注意。
以上就是本篇文章的所有内容了,我是LeHung,我们下期再见!!!更多精彩内容合集可访问项目:https://github.com/Chang-LeHu...
关注公众号:一无是处的研究僧,了解更多计算机(Java、Python、计算机系统基础、算法与数据结构)知识。