小波包能量 - python代码讲解
小波包能量 - python代码讲解
-
- **1、本文背景**
- **2、小波包分解介绍**
- **3、文件介绍**
- **4、读取数据**
-
- 4.1 定义一个数据读取函数
- 4.2画时域图
- **5、进行小波包变换**
- **6、绘制每一层小波分解时域图**
- **7、绘制小波包能量图**
- **8、正常状态轴承小波包能量图**
- **9、总结**
代码参见:https://github.com/HappyBoy-cmd/fault_diagnosis_signal_processing
参考资料
小波包变换/能量特征提取/结果图绘制-python代码
代码:小波包分解与重构、小波包能量特征提取
欢迎关注我的公众号《故障诊断与python学习》
1、本文背景
本文使用的是CWRU轴承数据进行演示,能够通过小波包能量区分正常与故障轴承
2、小波包分解介绍
小波包是为了克服小波分解在高频段的频率分辨率较差,而在低频段的时间分辨率较差的问题的基础上而提出的。
它是一种更精细的信号分析的方法,提高了信号的时域分辨率。
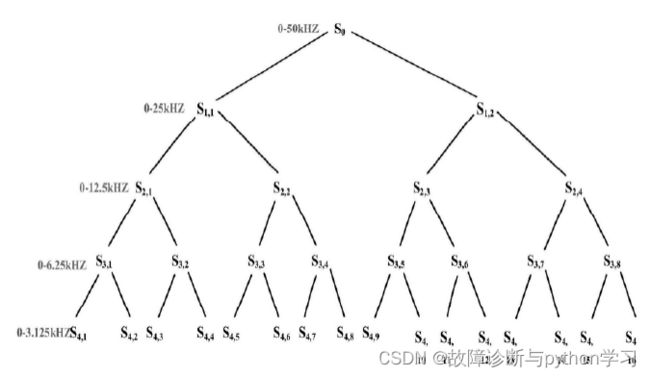
下面是两者的对比图:

下面是原始频率段为50kHz,然后通过层数分解成低频和高频段。比如S1,1就是0-25kHz,比如S1,2就是25-50kHz,
3、文件介绍
其中1730_12k_0.007-InnerRace.mat为内圈故障数据
1730_48k_Normal.mat为正常数据
4、读取数据
首先导入所需包
import scipy.io as scio #导入scio包
import numpy as np
import matplotlib.pyplot as plt
import os
from sklearn import preprocessing
import pywt
import pywt.data
import pandas as pd
中文宋体4号,英文数字用Times New Roman字体
from matplotlib import rcParams
config = {
"font.family": 'serif', # 衬线字体
"font.size": 10, # 相当于小四大小
"font.serif": ['SimSun'], # 宋体
"mathtext.fontset": 'stix', # matplotlib渲染数学字体时使用的字体,和Times New Roman差别不大
'axes.unicode_minus': False # 处理负号,即-号
}
rcParams.update(config)
4.1 定义一个数据读取函数
def DataAcquision(file_Path):
"""
fun: 从cwru mat文件读取加速度数据
param file_path: mat文件绝对路径
return accl_data: 加速度数据,array类型
"""
data = scio.loadmat(file_path) # 加载mat数据
data_key_list = list(data.keys()) # mat文件为字典类型,获取字典所有的键并转换为list类型
accl_key = data_key_list[3] # 获取'X108_DE_time'
accl_data = data[accl_key].flatten() # 获取'X108_DE_time'所对应的值,即为振动加速度信号,并将二维数组展成一维数组
return accl_data
首先以内圈故障数据进行演示
file_path = r'E:/研究生/pytorch/CSDN代码/第3篇-小波包能量/1730_12k_0.007-InnerRace.mat' #文件夹路径
data_arr = DataAcquision(file_path) # 加载mat数据
print(data_arr)
结果输出为>>>
[ 0.22269856 0.09323776 -0.14651649 ... -0.36125573 0.31138814
0.17055689]
4.2画时域图
plt.figure(figsize=(12,3))
plt.plot(data)
5、进行小波包变换
(1) 首先打印小波家族,看看有哪些小波函数
pywt.families()
#pywt.families(short=False)
结果如下:
['haar', 'db', 'sym', 'coif', 'bior', 'rbio', 'dmey', 'gaus', 'mexh', 'morl', 'cgau', 'shan', 'fbsp', 'cmor']
可见自带有14种小波函数,比如常见的 haar, db, morl
(2) 然后进行小波包变换
该方法输入原始信号data_arr, 小波函数选择’db1’,模式选择’symmetric’,以及最大的分解层数为3。返回wp是小波包树,根据小波包树我们可以提取分解系数。
#根据频段频率(freq)进行排序
wp = pywt.WaveletPacket(data=data_arr, wavelet='db1',mode='symmetric',maxlevel=3) #选用db1小波,分解层数为3
#根据频段频率(freq)进行排序
print('第一层小波包节点:',[node.path for node in wp.get_level(1, 'freq')]) # 第一层小波包节点
print('第二层小波包节点:',[node.path for node in wp.get_level(2, 'freq')]) # 第二层小波包节点
print('第三层小波包节点:',[node.path for node in wp.get_level(3, 'freq')]) # 第三层小波包节点
输出结果:
第一层小波包节点: ['a', 'd']
第二层小波包节点: ['aa', 'ad', 'dd', 'da']
第三层小波包节点: ['aaa', 'aad', 'add', 'ada', 'dda', 'ddd', 'dad', 'daa']
提取分解系数:下面aaa是小波包变换第三层第一个的分解系数
aaa = wp['aaa'].data
print(aaa)
print('aaa的长度:',aaa.shape[0])
print('data_arr的长度:',data_arr.shape[0])
print('理论上第3层每个分解系数的长度:',data_arr.shape[0]/8)
输出结果:
[ 0.13742877 0.02521155 -0.30747749 ... -0.14569862 -0.28215109
0.57900413]
aaa的长度: 15365
data_arr的长度: 122917
理论上第3层每个分解系数的长度: 15364.625
6、绘制每一层小波分解时域图
(1) 所以可以使用下面的方法提取每一层的每个节点的小波系数,当然这个方法不太方便,需要一个一个的写,后面有更好的方法:
a = wp['a'].data #第1个节点
d = wp['d'].data #第2个节点
#第二层
aa = wp['aa'].data
ad = wp['ad'].data
dd = wp['dd'].data
da = wp['da'].data
#第三层
aaa = wp['aaa'].data
aad = wp['aad'].data
ada = wp['add'].data
add = wp['ada'].data
daa = wp['dda'].data
dad = wp['ddd'].data
dda = wp['dad'].data
ddd = wp['daa'].data
(2) 绘制小波图
plt.figure(figsize=(15, 10))
plt.subplot(4,1,1)
plt.plot(data_arr)
#第一层
plt.subplot(4,2,3)
plt.plot(a)
plt.subplot(4,2,4)
plt.plot(d)
#第二层
plt.subplot(4,4,9)
plt.plot(aa)
plt.subplot(4,4,10)
plt.plot(ad)
plt.subplot(4,4,11)
plt.plot(dd)
plt.subplot(4,4,12)
plt.plot(da)
#第三层
plt.subplot(4,8,25)
plt.plot(aaa)
plt.subplot(4,8,26)
plt.plot(aad)
plt.subplot(4,8,27)
plt.plot(add)
plt.subplot(4,8,28)
plt.plot(ada)
plt.subplot(4,8,29)
plt.plot(dda)
plt.subplot(4,8,30)
plt.plot(ddd)
plt.subplot(4,8,31)
plt.plot(dad)
plt.subplot(4,8,32)
plt.plot(daa)
结果输出:
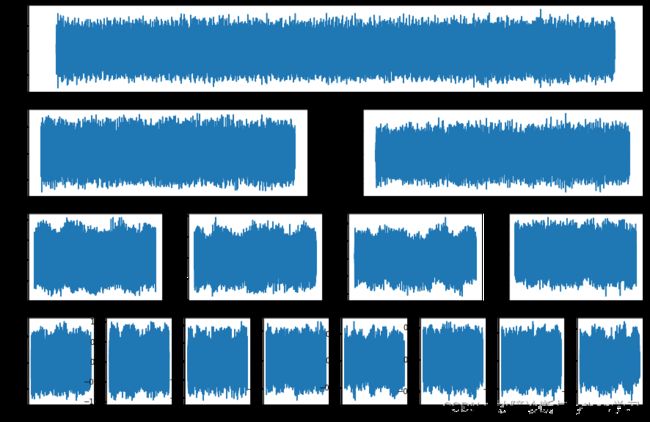
(3) 使用的wpd_plt(signal,n)将上面的代码优化和封装了,signal代表输入信号,n代表分解层数
def wpd_plt(signal,n):
'''
fun: 进行小波包分解,并绘制每层的小波包分解图
param signal: 要分解的信号,array类型
n: 要分解的层数
return: 绘制小波包分解图
'''
#wpd分解
wp = pywt.WaveletPacket(data=signal, wavelet='db1',mode='symmetric',maxlevel=n)
#计算每一个节点的系数,存在map中,key为'aa'等,value为列表
map = {}
map[1] = signal
for row in range(1,n+1):
lev = []
for i in [node.path for node in wp.get_level(row, 'freq')]:
map[i] = wp[i].data
#作图
plt.figure(figsize=(15, 10))
plt.subplot(n+1,1,1) #绘制第一个图
plt.plot(map[1])
for i in range(2,n+2):
level_num = pow(2,i-1) #从第二行图开始,计算上一行图的2的幂次方
#获取每一层分解的node:比如第三层['aaa', 'aad', 'add', 'ada', 'dda', 'ddd', 'dad', 'daa']
re = [node.path for node in wp.get_level(i-1, 'freq')]
for j in range(1,level_num+1):
plt.subplot(n+1,level_num,level_num*(i-1)+j)
plt.plot(map[re[j-1]]) #列表从0开始
wpd_plt(signal=data_arr, n=3)
输出结果:

与前面一样的效果,只是封装成了wpd_plt(signal,n)函数
7、绘制小波包能量图
def DataAcquision(file_Path):
"""
fun: 从cwru mat文件读取加速度数据
param file_path: mat文件绝对路径
return accl_data: 加速度数据,array类型
"""
data = scio.loadmat(file_path) # 加载mat数据
data_key_list = list(data.keys()) # mat文件为字典类型,获取字典所有的键并转换为list类型
accl_key = data_key_list[3] # 获取'X108_DE_time'
accl_data = data[accl_key].flatten() # 获取'X108_DE_time'所对应的值,即为振动加速度信号,并将二维数组展成一维数组
return accl_data
file_path = r'E:/研究生/pytorch/CSDN代码/第3篇-小波包能量/1730_12k_0.007-InnerRace.mat' #文件夹路径
data_arr = DataAcquision(file_path) # 加载mat数据
wp = pywt.WaveletPacket(data=data_arr, wavelet='db1',mode='symmetric',maxlevel=3) #选用db1小波,分解层数为3
n = 3
re = [] #第n层所有节点的分解系数
for i in [node.path for node in wp.get_level(n, 'freq')]:
re.append(wp[i].data)
#第n层能量特征
energy = []
for i in re:
energy.append(pow(np.linalg.norm(i,ord=None),2))
for i in range(len(energy)):
print('最后一层第{0}个小波的能量为:{1}'.format(i, energy[i]))
输出结果:
最后一层第0个小波的能量为:601.1287769222096
最后一层第1个小波的能量为:1166.6942072871639
最后一层第2个小波的能量为:1574.8261014889372
最后一层第3个小波的能量为:3020.053424520311
最后一层第4个小波的能量为:3624.086184449376
最后一层第5个小波的能量为:1496.5850478295588
最后一层第6个小波的能量为:317.91754565296947
最后一层第7个小波的能量为:287.5823913938649
接下来绘制最后一层能量图
# 创建一个点数为 8 x 6 的窗口, 并设置分辨率为 80像素/每英寸
plt.figure(figsize=(10, 7), dpi=80)
# 再创建一个规格为 1 x 1 的子图
# plt.subplot(1, 1, 1)
# 柱子总数
N = 8
values = energy
# 包含每个柱子下标的序列
index = np.arange(N)
# 柱子的宽度
width = 0.45
# 绘制柱状图, 每根柱子的颜色为紫罗兰色
p2 = plt.bar(index, values, width, label="num", color="#87CEFA")
# 设置横轴标签
plt.xlabel('clusters')
# 设置纵轴标签
plt.ylabel('Wavel energy')
# 添加标题
plt.title('Cluster Distribution')
# 添加纵横轴的刻度
plt.xticks(index, ('7', '8', '9', '10', '11', '12', '13', '14'))
# plt.yticks(np.arange(0, 10000, 10))
# 添加图例
plt.legend(loc="upper right")
plt.show()
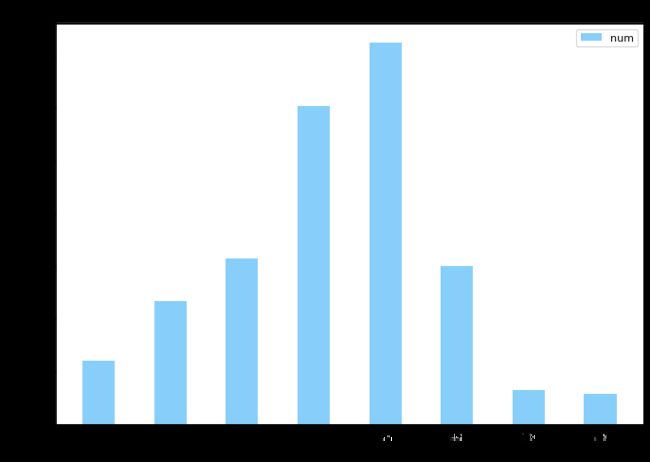
原始频率为12000Hz,分成8份,每份为1500Hz,因此
7是指0-1500Hz频段
8是指1500-3000Hz频段
...
13是指9000-10500Hz频段
14是指10500-12000Hz频段
由图可知,内圈故障的小波包能量集中在10和11频段,即在4500-7500Hz范围内。
关键程序理解
map = {}
map[1] = data_arr
n = 3
for row in range(1,n+1):
for i in [node.path for node in wp.get_level(row, 'freq')]:
print(i)
map[i] = wp[i].data
输出结果:
a
d
aa
ad
dd
da
aaa
aad
add
ada
dda
ddd
dad
daa
由打印结果可知,i为每个小波包的名字
print(map)
输出结果:
{1: array([ 0.22269856, 0.09323776, -0.14651649, ..., -0.36125573,
0.31138814, 0.17055689]),
'a': array([ 0.22340072, 0.02170835, 0.12542601, ..., 0.71086224,
-0.03526171, 0.24120386]),
'd': array([ 0.09154261, -0.22891395, 0.22604248, ..., 0.47677963,
-0.47563104, 0. ]),
'aa': array([0.17331828, 0.02103535, 0.2048307 , ..., 0.1387196 , 0.47772172,
0.34111377]),
'ad': array([ 0.14261804, 0.15634381, -0.01331968, ..., -0.00129948,
0.5275893 , 0. ]),
'dd': array([ 0.22659701, 0.21352098, 0.01884248, ..., -0.44036164,
0.67345605, 0. ]),
'da': array([-0.09713621, 0.10615136, 0.0300505 , ..., -0.5183305 ,
0.00081218, 0. ]),
'aaa': array([ 0.13742877, 0.02521155, -0.30747749, ..., -0.14569862,
-0.28215109, 0.57900413]),
'aad': array([ 0.1076803 , 0.26446281, 0.54041151, ..., -0.30006909,
-0.47833023, 0.0965964 ]),
'add': array([-0.00970558, -0.01039474, -0.33802998, ..., 0.43468382,
-0.00752326, 0.37306197]),
'ada': array([ 0.21139796, -0.00844214, -0.24752111, ..., -0.83129188,
-0.00936101, 0.37306197]),
'dda': array([ 0.31121041, -0.01154333, 0.52823646, ..., -0.77501098,
-1.17839572, 0.47620534]),
'ddd': array([ 0.00924615, 0.03819061, -0.29392413, ..., 0.77053148,
-0.55563032, 0.47620534]),
'dad': array([-0.14374602, 0.02245493, -0.196294 , ..., -0.00557066,
0.37024793, 0.00057429]),
'daa': array([ 0.00637467, 0.02004289, -0.02630271, ..., 0.24780825,
-0.36278209, 0.00057429])}
可知map是个字典,key为小波包名,value为每个小波包的系数
8、正常状态轴承小波包能量图
def DataAcquision(file_Path):
"""
fun: 从cwru mat文件读取加速度数据
param file_path: mat文件绝对路径
return accl_data: 加速度数据,array类型
"""
data = scio.loadmat(file_path) # 加载mat数据
data_key_list = list(data.keys()) # mat文件为字典类型,获取字典所有的键并转换为list类型
accl_key = data_key_list[3] # 获取'X108_DE_time'
accl_data = data[accl_key].flatten() # 获取'X108_DE_time'所对应的值,即为振动加速度信号,并将二维数组展成一维数组
return accl_data
file_path = r'E:/研究生/pytorch/CSDN代码/第3篇-小波包能量/1730_48k_Normal.mat' #文件夹路径
data_arr = DataAcquision(file_path) # 加载mat数据
wp = pywt.WaveletPacket(data=data_arr, wavelet='db1',mode='symmetric',maxlevel=3) #选用db1小波,分解层数为3
#------计算每层小波包能量------#
n = 3
re = [] #第n层所有节点的分解系数
for i in [node.path for node in wp.get_level(n, 'freq')]:
re.append(wp[i].data)
#第n层能量特征
energy = []
for i in re:
energy.append(pow(np.linalg.norm(i,ord=None),2))
for i in energy:
print(i)
#-------绘制小波包能量图------——#
# 创建一个点数为 8 x 6 的窗口, 并设置分辨率为 80像素/每英寸
plt.figure(figsize=(10, 7), dpi=80)
# 再创建一个规格为 1 x 1 的子图
# plt.subplot(1, 1, 1)
# 柱子总数
N = 8
values = energy
# 包含每个柱子下标的序列
index = np.arange(N)
# 柱子的宽度
width = 0.45
# 绘制柱状图, 每根柱子的颜色为紫罗兰色
p2 = plt.bar(index, values, width, label="num", color="#87CEFA")
# 设置横轴标签
plt.xlabel('clusters')
# 设置纵轴标签
plt.ylabel('Wavel energy')
# 添加标题
plt.title('Cluster Distribution')
# 添加纵横轴的刻度
plt.xticks(index, ('7', '8', '9', '10', '11', '12', '13', '14'))
# plt.yticks(np.arange(0, 10000, 10))
# 添加图例
plt.legend(loc="upper right")
plt.show()
输出结果:
1021.5168476406585
452.3749624106609
309.1511931365197
142.1466500905686
38.92694236720233
77.92200291274384
45.94133962149062
20.05028055171906
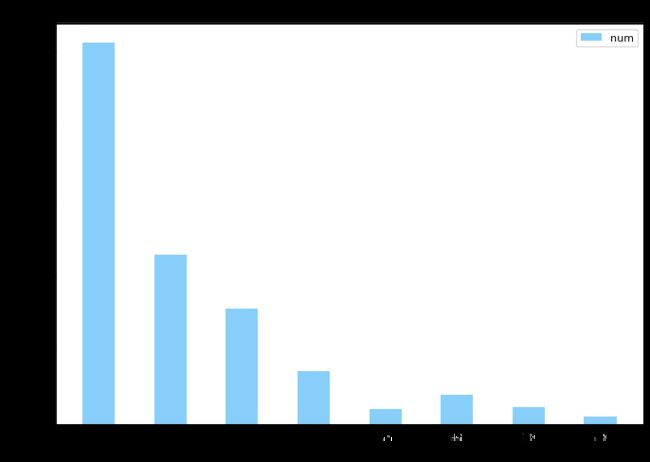
可知正常状态能量集中在低频段0-1500Hz内。
9、总结
(1)、本文对小波包分解及小波包能量进行了程序实现及讲解,并用CWRU轴承数据进行了演示
(2)、正常轴承小波包能量集中在低频(0-1500Hz),内圈故障轴承小波包能量集中在中高频(4500-7500Hz)
(3)、小波包能够较好区分正常轴承与内圈故障轴承