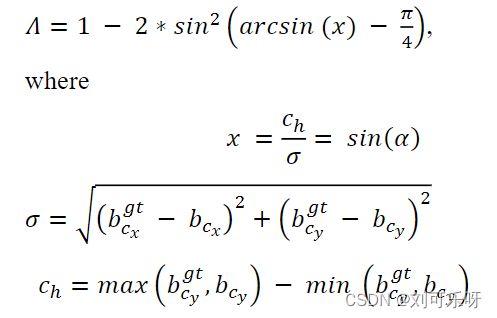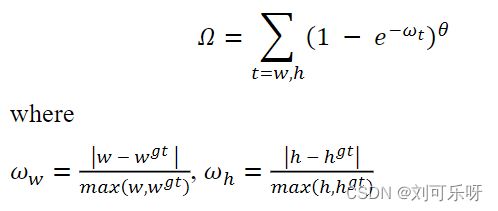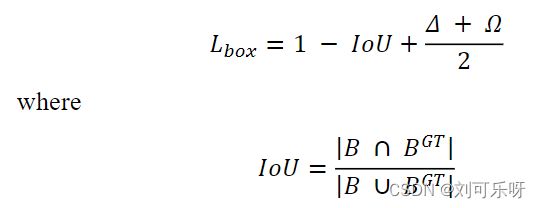【最新损失函数SIOU全文翻译】超越YOLO-V5等先进模型提高了+3.6%
SIoU Loss: More Powerful Learning for Bounding Box RegressionZhora Gevorgyan
文章https://arxiv.org/abs/2205.12740
目录
Abstract
Introduction
Methods
Angle cost
Distance cost
Shape cost
Training
Simulation Experiment
Implementation test
Results and Discussion
Conclusion
Abstract
目标检测是计算机视觉任务中的核心问题之一,其有效性在很大程度上取决于损失函数的定义——衡量您的ML模型预测预期结果的准确程度。传统的目标检测损失函数依赖于边界框回归指标的聚合,例如预测框和真实框(即GIoU、CIoU、ICIoU等)的距离、重叠区域和纵横比。然而,迄今为止提出和使用的方法都没有考虑期望的地面盒和预测的“实验”盒之间不匹配的方向。这种不足导致收敛速度较慢且效率较低,因为预测框可能在训练过程中“四处游荡”并最终产生更差的模型。在本文中,提出了一种新的损失函数SIoU,其中考虑到所需回归之间的向量角度,重新定义了惩罚指标。应用于传统的神经网络和数据集,表明 SIoU 提高了训练的速度和推理的准确性。在许多模拟和测试中揭示了所提出的损失函数的有效性。特别是,将SIoU应用于COCO-train/COCO-val与其他损失函数相比,提高了+2.4% ([email protected]:0.95) 和+3.6%([email protected])。
Introduction
目标检测是计算机视觉任务中的关键问题之一,因此几十年来它受到了相当多的研究关注。很明显,要解决这个问题,需要在神经网络方法可接受的概念中定义问题。在这些概念中,所谓的损失函数(LF)的定义起着重要作用。后者作为一种惩罚措施,需要在训练期间最小化,并且理想情况下可以将勾勒出对象的预测框与相应的真实框匹配。为对象检测问题定义LF有不同的方法,这些方法考虑到框的以下“不匹配”度量的某种组合:框中心之间的距离、重叠区域和纵横比。最近 Rezatofighi 等人。声称广义 IoU (GIoU) LF 优于其他标准LF的最先进的对象检测方法。虽然这些方法对训练过程和最终结果都产生了积极影响,但我们认为仍有很大改进的空间。因此,与用于计算地面实况和模型预测图像中对象的边界框不匹配的惩罚的传统指标并行——即距离、形状和 IoU,我们建议还要考虑不匹配的方向。这种添加极大地帮助了训练过程,因为它导致预测框相当快地漂移到最近的轴,并且随后的方法只需要一个坐标X或Y的回归。简而言之,添加角惩罚成本有效地减少了总度数自由。
Methods
让我们定义应该有助于 SCYLLA-IoU (SIoU) 损失函数估计的指标。 SIoU 损失函数由 4 个代价函数组成:
Angle cost
Distance cost
Shape cost
IoU cost
Angle cost
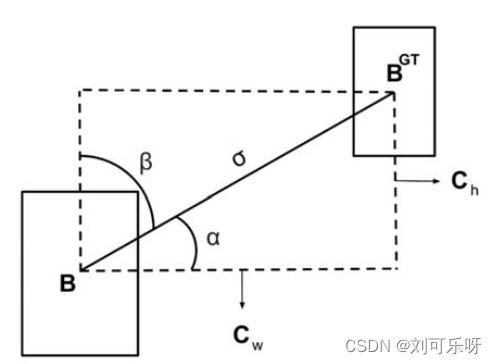
图 1. 计算角度成本对损失函数的贡献的方案。
添加此角度感知LF组件背后的想法是最大限度地减少与距离相关的“奇妙”中的变量数量。基本上,模型将尝试首先将预测带到X或Y轴(以最接近者为准),然后沿着相关轴继续接近。为了实现这一点,收敛过程将首先尝试最小化![]() 如果
如果![]() 否则最小化
否则最小化![]()
为了首先实现这一点,我们引入并定义了LF组件,方法如下:
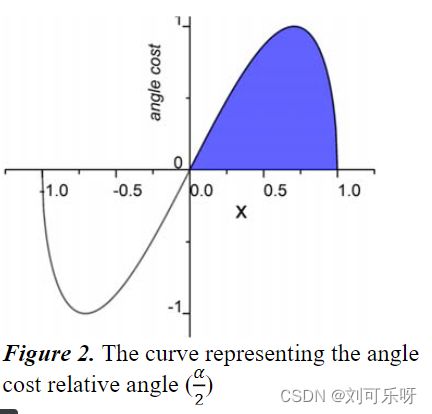
Angle cost的曲线如图2所示。
Distance cost
考虑到上面定义的Angle cost,重新定义了Distance cost:
可以看出,当 → 0 时,Distance cost的贡献大大降低。 相反 与Π/4越接近,贡献越大。 随着角度的增加,问题变得更加困难。 因此,随着角度的增加,γ被赋予时间优先的距离值。 请注意,当 → 0 时,距离成本将变得常规。
Shape cost
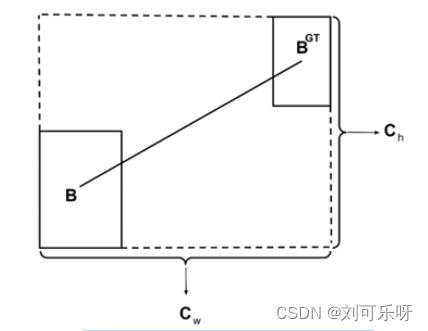
图3. 计算地面实况边界框与其预测之间的距离的方案。
Shape cost被定义为:
的值定义了每个数据集的Shape cost及其值是唯一的。的值是这个等式中非常重要的一项,它控制着对Shape cost的关注程度。 如果的值设置为1,它将立即优化形状,从而损害形状的自由移动。 为了计算的值,对每个数据集使用遗传算法,实验上的值接近4,作者为此参数定义的范围是2到6。在地面实况边界框及其预测之间。
图4. IoU 组件贡献关系示意图。
最后让我们定义损失函数
Training
为了评估所提出的损失函数的有效性,该模型在COCO数据集上进行了训练,该数据集包含200+K图像,标记有150万个对象实例。 为了比较训练效果,我们使用提出的SIoU和最先进的 CIoU损失函数对300个epoch的COCO-train进行了训练,并在COCO-val上进行了测试。
Simulation Experiment
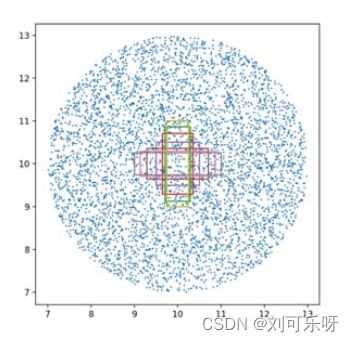
正如[CIoU论文]提出的,使用模拟实验来进一步评估回归过程。在模拟实验中,边界框之间的大部分关系都涵盖了距离、比例和纵横比。特别是,选择了7个单元框(即每个框的面积为 1),具有不同的纵横比(即 1:4、1:3、1:2、1:1、2:1、3:1 和4:1) 作为目标框。不失一般性,7个目标框的中心点固定在(10, 10)。锚框均匀分布在5000个点上(见图 5)。(i)距离:在以 (10, 10)为中心、半径为3的圆形区域内均匀选择5000个点来放置具有7个比例和7个纵横比的锚框。在这些情况下,包括重叠和非重叠框。 (ii)比例:对于每个点,锚框的面积分别设置为 0.5、0.67、0.75、1、1.33、1.5 和 2。 (iii) 纵横比:对于给定的点和比例,采用7个纵横比,即遵循与目标框相同的设置。所有5000 ×7 ×7的锚框都应该适合每个目标框。综上所述,总共有1715000 =7 ×7 ×7 ×5000个回归案例。
图 5. 以 (10,10) 为中心的模拟 5000 个锚框的摘要图像。
总最终误差按以下方式定义:
具有步进学习率调度器的Adam优化器用于训练。 步进学习的初始学习率和步长分别设置为0.1和80。 训练持续了100个epoch。
Implementation test
最终的损失函数由两项组成:分类损失和框损失。
其中![]() 是焦点损失,
是焦点损失,![]() 和
和![]() 分别是框和分类损失权重。为了计算
分别是框和分类损失权重。为了计算![]() 、
、![]() 、,使用了遗传算法。 为了训练遗传算法,从训练集中提取一个小子集并计算值,直到发现适应值小于阈值或过程超过最大允许迭代次数。
、,使用了遗传算法。 为了训练遗传算法,从训练集中提取一个小子集并计算值,直到发现适应值小于阈值或过程超过最大允许迭代次数。
Results and Discussion
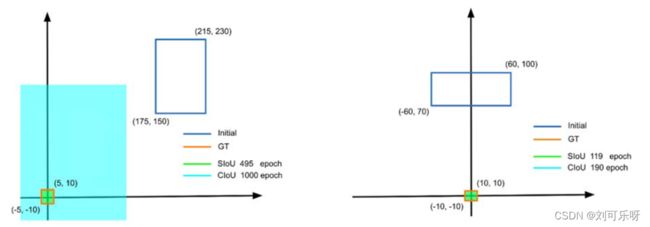
图6. 模拟示例显示放置在轴上的框与远离轴的框的收敛。 显然是 SIoU 方法。
一个简单的测试我们比较了两种收敛情况——当初始框放置在其中一个轴上时(参见图 6,右窗格)和当框远离轴时(参见图 6,左窗格)。显然,当初始预测框远离地面实况框的X/Y轴时,SIoU 控制训练的优势变得更加明显:SIoU训练在495个epoch内收敛到地面实况,而传统的CIoU没有找到它,即使在1000个epoch中。
图7. CIoU 和 SIoU 的 1715000 个模拟案例的总误差曲面图。
图7包含CIoU和SIoU的仿真实验图。 所有1715000个回归案例都汇总在3D图中,其中X和Y轴是框中心点的坐标,Z是误差。 如您所见,建议的SIoU损失的最大误差几乎比CIoU小两个数量级。 另请注意,在SIoU的情况下,误差表面要平滑得多,这表明SIoU的总误差对于所有模拟情况都是最小的。
图 8. 通过训练迭代绘制来自 CIoU 和 SIoU 损失的误差。
图8展示了CIoU和SIoU驱动训练的另一个比较结果。对于SIoU,总误差对迭代的依赖性要大得多,最终值也较低。
为了评估SIoU的效率,我们还比较了它对我们专有的Scylla-Net神经网络的影响。 Scylla-Net 是一种基于卷积的神经网络,它使用遗传算法为给定预定义层类型的特定数据集定义其架构。 在模拟不同尺寸的暗网模型时,我们使用了两种尺寸的小模型:Scylla-Net-S和大模型:Scylla-Net-L。
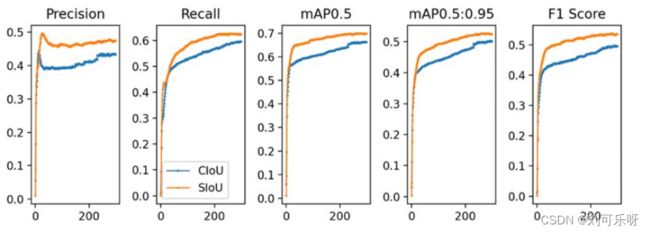
图9. 使用建议的SIoU和广泛使用的CIoU损失函数在COCO-train数据集上训练期间监控的参数。
对于全功能测试,我们训练了模型并监控了300轮训练的所有参数。 相应的图如图9所示。显然,所有监控的指标不仅在训练期间显着提高,而且达到更好的最终值。
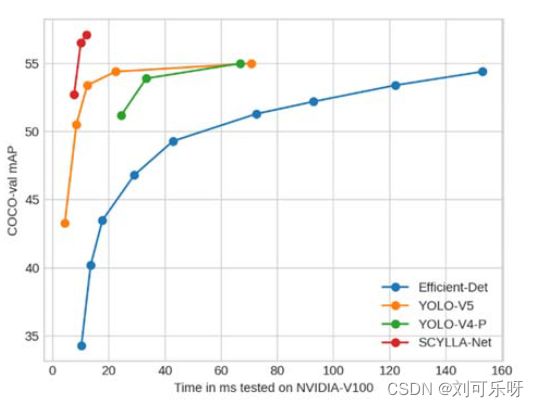
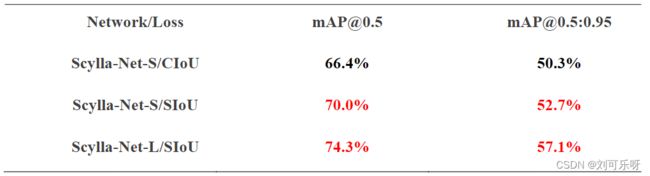
即COCO-val上损失函数的mAP为52.7% [email protected]:0.95(包括预处理、推理和后处理为 7.6ms)和70% [email protected],而CIoU损失分别仅为50.3%和66.4%。更大的模型可以达到57.1% [email protected]:0.95(12ms 包括预处理、推理和后处理)和74.3% [email protected],而其他架构如Efficient-Det-d7x、YOLO-V4和YOLO-V5可以达到最大[email protected] :分别为 54.4% (153ms)、47.1% (26.3ms) 和 50.4%(使用 fp16进行6.1ms 测试)的0.95。 请注意,YOLO-V5x6-TTA在COCO-val上可以达到约55%,但推理时间非常慢(浮点精度为16时约为72ms)。图10总结了不同模型与[email protected]:0.95的推理时间。显然,Scylla-Net的mAP值较高,而模型推理时间远低于比较模型的推理时间。
图10.不同模型相对于[email protected]:0.95 的每张图像推理时间。
表1. 使用CIoU损失、SIoU和SIoU训练的Scylla-Net的mAP指标比较应用于更大的Scylla模型
最后,为了评估模型性能的改进,我们通过使用SIoU训练的Scylla-Net运行不同模型/方法呈现的样本图像。图11给出了一些示例。 注意比较模型的假阴性和报告概率的差异。
Conclusion
在本文中,提出了一种新的边界框回归损失函数,可以极大地改善目标检测算法的训练和推理。 通过在损失函数成本中引入方向性,与现有方法(例如CIoU损失)相比,在训练阶段实现了更快的收敛,并且在推理方面具有更好的性能。 所提出的改进有效地降低了自由度(一个坐标对两个),并且收敛更快、更准确。 与广泛使用的最先进的方法和报告的测量改进相比,这些声明得到了验证。 所提出的损失函数可以很容易地包含在任何对象检测管道中,并将有助于实现卓越的结果。