RSA加密算法
RSA算法基于一个十分简单的数论事实:将两个大素数相乘十分容易,但那时想要对其乘积进行因式分解却极其困难,因此可以将乘积公开作为加密密钥。RSA算法是第一个能同时用于加密和数字签名的算法,也易于理解和操作。
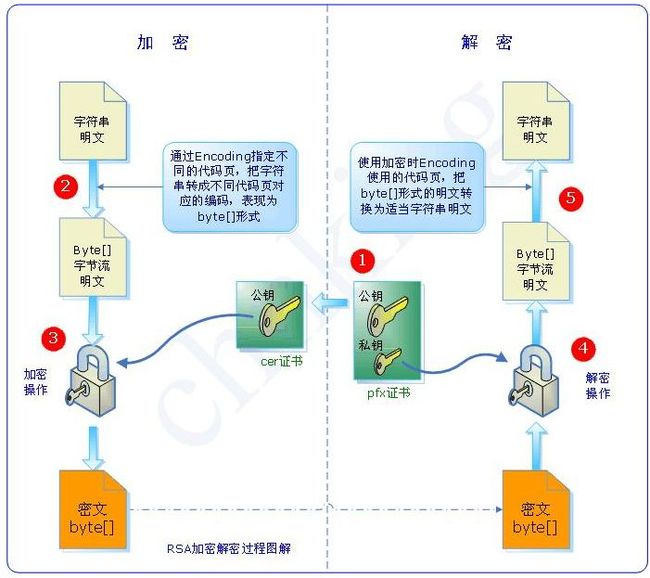
原理图:
C# 代码实现:
算法介绍:
算法的名字以发明者的名字命名:Ron Rivest, AdiShamir 和Leonard Adleman。早在1973年,英国国家通信总局的数学家Clifford Cocks就发现了类似的算法。但是他的发现被列为绝密,直到1998年才公诸于世。
RSA算法是一种非对称密码算法,所谓非对称,就是指该算法需要一对密钥,使用其中一个加密,则需要用另一个才能解密。
RSA的算法涉及三个参数,n、e1、e2。
其中,n是两个大质数p、q的积,n的二进制表示时所占用的位数,就是所谓的密钥长度。
e1和e2是一对相关的值,e1可以任意取,但要求e1与(p-1)*(q-1)互质;再选择e2,要求(e2*e1)mod((p-1)*(q-1))=1。
(n及e1),(n及e2)就是密钥对。
RSA加解密的算法完全相同,设A为明文,B为密文,则:A=B^e1 mod n;B=A^e2 mod n;
e1和e2可以互换使用,即:A=B^e2 mod n;B=A^e1 mod n;