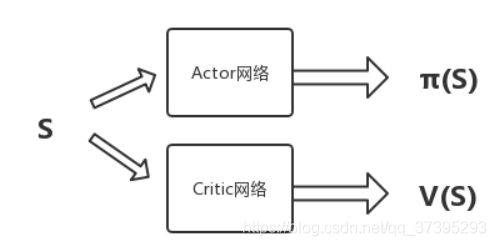
入门篇---Actor-Critic系列（pytorch）

入门篇—Actor-Critic系列（pytorch）

A3C

算法理论

与传统的Actor-Critic算法相比，A3C算法有更好的收敛性，同时避免了经验回访相关性过强的问题，做到了异步并发的学习模型。
优化部分主要有三点：异步训练框架，网络结构优化，Critic评估点的优化。其中异步训练框架是最大的优化。

异步训练框架

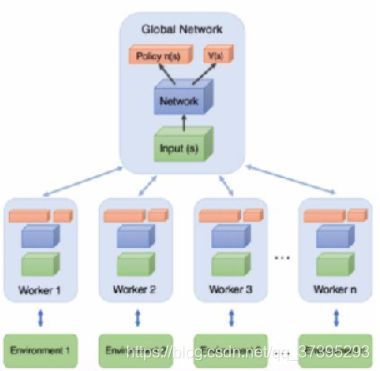
主要框架为一个公共神经网络，下面有n个子网络。他们的网络架构和初始参数都是完全一样的。区别在于，每个子网络独立的在环境中进行交互，但是每隔一段时间子网络会将自己的累计梯度更新公共部分的网络模型参数。公共部分的网络模型就是我们要学习的模型，而子网络里的网络模型主要是用于和环境交互使用的，这些子网络里的模型可以帮助线程更好的和环境交互，拿到高质量的数据帮助模型更快收敛。

网络结构优化

Critic评估点优化

引入Dueling-DQN中优势函数的概念，使用优势函数$A$来作为critic的评估点，即

其中$Q(S,A)$一般通过单步采样近似估计，即又是函数表示为

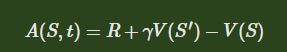
在A3C中，采样更进一步，使用了N步采样，以加速收敛

同时引入了策略$\pi$的熵，由此，最终的策略参数更新变成下式

A2C

异步优势演员批评方法（A3C）结合了一些关键思想：

1、对经验的固定长度段（例如20个时间步长，代码中使用的是5个时间步长）进行操作的一种更新方案，并使用这些段来计算收益和优势函数的估计量。（Critic评估点优化）
2、在策略和价值功能之间共享层次的体系结构。（网络结构优化）
3、异步更新。

作为异步实现的替代方法，研究人员发现可以编写一个同步的确定性实现，该实现要等每个参与者完成其经验之后再执行更新，对所有参与者进行平均。此方法的一个优势是，它可以更有效地使用GPU，在批量较大时，GPU的性能最佳。该算法被称为A2C，是优势演员评论家（actor critic）的简称。

代码

import math
import random

import gym
import numpy as np

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.distributions import Categorical
import matplotlib.pyplot as plt

from multiprocessing_env import SubprocVecEnv

use_cuda = torch.cuda.is_available()
device   = torch.device("cuda" if use_cuda else "cpu")

class ActorCritic(nn.Module):
    def __init__(self, inputs, outputs, hidden_size, std=0.0):
        super(ActorCritic, self).__init__()
        self.Actor = nn.Sequential(
            nn.Linear(inputs, hidden_size),
            nn.ReLU(),
            nn.Linear(hidden_size, outputs),
            #使得在softmax操作之后在dim这个维度相加等于1
            #注意，默认的方法已经弃用，最好在使用的时候声明dim
            nn.Softmax(dim=1)

        )
        self.Critic = nn.Sequential(
            nn.Linear(inputs, hidden_size),
            nn.ReLU(),
            nn.Linear(hidden_size,1)
        )
    def forward(self,x):
        value = self.Critic(x)
        probs = self.Actor(x)
        #分类,对actor输出的动作概率进行分类统计
        dist = Categorical(probs)
        return dist, value

def make_env():
    def _thunk():
        env = gym.make("CartPole-v0")
        return env
    return _thunk

#通过N步采样，以加速收敛，这里是计算优势函数
def compute_returns(next_value, rewards, masks, gamma=0.99):
    R = next_value
    returns = []
    for step in reversed(range(len(rewards))):
        R = rewards[step] + gamma * R * masks[step]
        #list.insert(index, obj)，index -- 对象 obj 需要插入的索引位置。
        returns.insert(0, R)
    return returns

def test_env(model, env,vis=False):
    state = env.reset()
    if vis: env.render()
    done = False
    total_reward = 0
    while not done:
        state = torch.FloatTensor(state).unsqueeze(0).to(device)
        dist, _ = model(state)
        next_state, reward, done, _ = env.step(dist.sample().cpu().numpy()[0])
        state = next_state
        if vis: env.render()
        total_reward += reward
    return total_reward

def plot(frame_idx, rewards):
    plt.figure(figsize=(20,5))
    plt.subplot(131)
    plt.title('frame %s. reward: %s' % (frame_idx, rewards[-1]))
    plt.plot(rewards)
    plt.show()

def main():
    num_envs = 16
    envs = [make_env() for i in range(num_envs)]
    envs = SubprocVecEnv(envs)
    env = gym.make("CartPole-v0")

    num_inputs = envs.observation_space.shape[0]
    num_outputs = envs.action_space.n
    # Hyper params:
    hidden_size = 256
    lr = 3e-4
    num_steps = 5

    model = ActorCritic(num_inputs,num_outputs,hidden_size).to(device)

    optimizer = optim.Adam(model.parameters())

    max_frames = 20000
    frame_idx = 0
    test_rewards = []
    state = envs.reset()

    while frame_idx < max_frames:

        log_probs = []
        values = []
        rewards = []
        masks = []
        entropy = 0

        #每个子网络运行num_steps个steps,实现n步采样
        for _ in range(num_steps):
            state = torch.FloatTensor(state).to(device)
            dist, value = model(state)
            action = dist.sample()
            next_state, reward, done, _ = envs.step(action.cpu().numpy())
            log_prob = dist.log_prob(action)
            entropy += dist.entropy().mean()

            #记录下这num_steps步的各子网络相关参数
            log_probs.append(log_prob)
            values.append(value)
            rewards.append(torch.FloatTensor(reward).unsqueeze(1).to(device))
            masks.append(torch.FloatTensor(1 - done).unsqueeze(1).to(device))

            state = next_state
            frame_idx += 1

            if frame_idx % 1000 == 0:
                test_rewards.append(np.mean([test_env(model, env) for _ in range(10)]))
                plot(frame_idx, test_rewards)

        #将子网络的参数传给主网络，并进行参数更新
        next_state = torch.FloatTensor(next_state).to(device)
        _, next_value = model(next_state)
        returns = compute_returns(next_value, rewards, masks)

        #将5个step的值串起来
        log_probs = torch.cat(log_probs)
        returns = torch.cat(returns).detach()
        values = torch.cat(values)

        advantage = returns - values
        #计算loss均值
        actor_loss = -(log_probs * advantage.detach()).mean()
        critic_loss = advantage.pow(2).mean()

        loss = actor_loss + 0.5 * critic_loss - 0.001 * entropy

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

if __name__ == '__main__':
    main()