相关系数excel_数学建模笔记——相关系数
今天写一个比较简单也比较常用的内容——相关系数。
相关系数,并不是一个陌生的概念,因为高中的时候好像就学过了。只不过那个时候没有讲太深入,当然啦,我这篇笔记也不会讲得多深入,能力达不到嘛。理解一下,会用就好。
相关系数,其实就是衡量两个变量之间相关性的大小的指标,常用的相关系数有两种,一种是pearson相关系数,也就是《概率论与数理统计》这本书里提到的,平时最为常用的相关系数。另一种称之为spearman相关系数,我也是在清风老师的课中第一次听说,它衡量的是两个变量的依赖性,唔,也可以理解为单调性啦。接下来我就介绍一下我学到的内容吧~
相关概念引入
总体与样本
总体与样本是初等统计学中最为基本的概念之一。在统计学中,我们时常要对一些对象,人,事,物等进行观察研究,希望发现它们运动变化过程中的一些内在的规律。但是,出于各种条件的限制,我们往往很难我们感兴趣的群体的全部信息。例如,我们想要知道中国大学生的每月平均消费水平,理想状态下,我们首先应该知道中国所有大学生每个人的平均月消费,再加总起来除以人数。但想想就知道,除非付出极大的代价,否则不可能获取到每一个人的花费信息。
但实际上,我们也没有太大必要进行这种普查性质的活动。我们可以首先根据地理位置或者其他指标选定一些学校,作为我们进行调查的学校。之后在这些学校里,我们又可以按照某种指标,或者尽可能多得选择一些学生进行询问。这样,我们就获得了研究对象中一部分学生的消费信息,之后就可以计算这部分学生的平均月消费,并且将它视为全部大学生的平均月消费。
在上面这个例子中,总体就是我们感兴趣的研究对象全体,也就是全中国的大学生。样本就是我们最后真正得到信息的那部分学生。而从总体中获得样本的过程,就称之为抽样。hhh这些高中应该都学过,简单说一下。
为什么要进行抽样获得样本呢?就是因为总体数据的获取过于困难,我们只好退而求其次,选择一个可以代表总体的样本,用这个样本的相关统计量,相关规律等来推测总体的相关统计量以及规律。 那为什么可以用样本的性质来代表或者推测总体的性质呢?这个我也不太清楚,因为大家都默认是这样的。
简单理解一下,个体的某些性质,我们是不好揣测的,特别是有些个体,本身就有较大的波动。所以观察个体的数据,我们很难得到什么一般性的结论。但许多个个体聚在一起,他们的行为,性质等可能会表现出某种同步性,或者说规律性。个体是特殊的,但总体中的个体又是普通的,统计学想要发掘的,大概就是个体中存在的共性。这种共性,或者说规律本身是固定的,观察数量的多少,主要决定着对这种规律的反映程度。数量越多,规律自然会更清晰更直观。因此,样本相对于总体,其区别可能就是对规律或者共性的反映清晰度不同,但本质上是一样的。那么,用样本估计总体或者代替总体,就无可厚非了。(以上全是瞎扯)
描述性统计
简单介绍一下样本的描述性统计。所谓描述性统计,就是通过表格,图形等手段从各个方面对数据进行展示的过程。其主要作用就是从总体上看一看数据变量的特征、分布、变化趋势等等。
简单的描述性统计主要有两个内容,一是对数据变量进行五数概括,看一看变量的位置分布;另一个就是展示一下数据变量的均值与方差。除此之外,出于美观以及方便的需要,我们还会把数据进行可视化操作,以更好地进行展示。
五数概括,就是指出变量数据的最小值、最大值、第一四分位数、中位数以及第三四分位数。很简单,首先把数据从小到大进行排序,第一个就是最小值,最后一个就是最大值,处于最中间位置的便是中位数的值了。对中位数左边的数据(除去中位数)计算中位数,即第一四分位数;对中位数右边的数据(除去中位数)计算中位数,即第三四分位数。如果进行比较明确的定义,数据变量
五数概括的目的在于描述变量的分布,观察变量的总体情况。相对于平均数或者中位数这种单一指标,五数概括包含的信息就更加充分了。
之后就是均值方差描述了。其中均值衡量的是样本数据的平均程度,就是常说的平均值,方差描述的是数据的分散程度。这两个统计量也是高中就学过的内容,均值
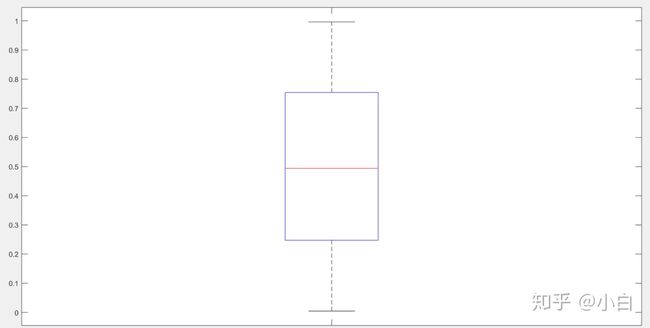
对于五数概括,matlab好像没有比较直接的函数,所以我们可以通过箱形图来看看它的五数。所谓箱形图,就是下方这种图。
最下方和最上方的黑色横线位置分别代表最大值和最小值。箱体的下方蓝线为第一四分位数,箱体的上方为第三四分位数,箱体中间的红线即为中位数。由于这是由均匀分布生成的数据,因此中位数好像就在正中央,但一般情况下并非如此。
如果想要查看四分位数或者中位数,直接点击相应的线就好了,matlab会自动显示出来。由上图我们可以看到,50%的数据都在40一下,而25%的数据都在100以上,这便可以理解为一个代表着“贫富差距”的箱型图了。
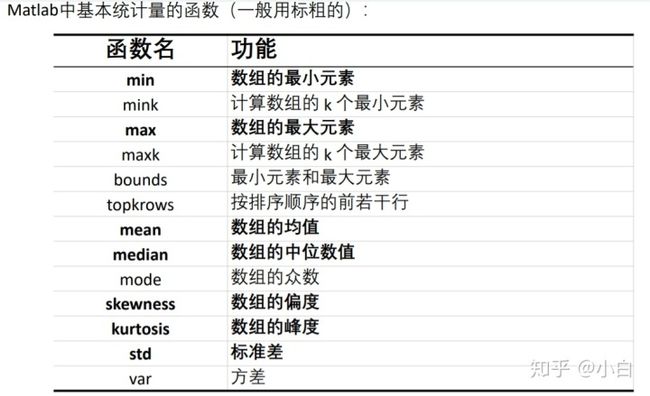
至于均值和方差,matlab中使用mean函数求均值,std函数求标准差(方差的平方根),var函数求方差,比较简单,此处不表。
xPearson相关系数
好的,现在介绍一下Pearson相关系数。
总体Pearson相关系数
顾名思义,就是总体数据的相关系数。如果两组数据
总体的方差为
上式中的协方差,简单来说,衡量的是两个变量之间的变化趋势。如果两个变量的变化趋势一致,即
那Pearson相关系数呢?其实就是两个变量的协方差除以它们的标准差,可以将其理解为对
唔,我可能解释的不是很好,知乎上有一个问题,大家可以去看一看,再理解一下。 [如何通俗易懂地解释「协方差」与「相关系数」的概念? - 知乎](https://www.zhihu.com/question/20852004)
样本相关系数
其实差不多,计算公式还是一样的,但是在具体的样本协方差,样本方差计算上,有一些小的差别。样本均值
总体的协方差
总体的方差
相关系数的性质
我们需要了解一些相关系数的性质以更好地使用它。
性质一说明,相关系数介于
同时,如果
性质二则指出,如果
注意
在使用相关系数的时候,有几个需要注意的点。
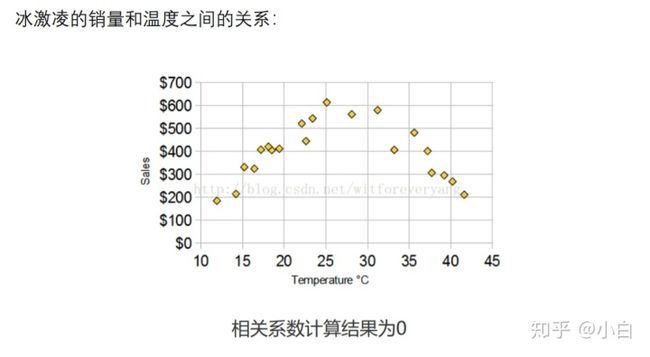
首先,相关系数刻画的是线性相关关系,也就是用来衡量两个变量线性相关程度的指标。如果你想使用相关系数来说明它们之间的相关程度,就必须得通过画散点图等手段,确认这两个变量是具有一定的线性相关性的。嗯,记住,相关系数只能说明线性相关程度。如果两个变量之间具有某种二次或者指数关系,它们仍然是具有相关性的,只是线性相关程度可能比较低罢了。所以千万不要看到相关系数很小就认为二者不相关,事实上只是线性不相关。
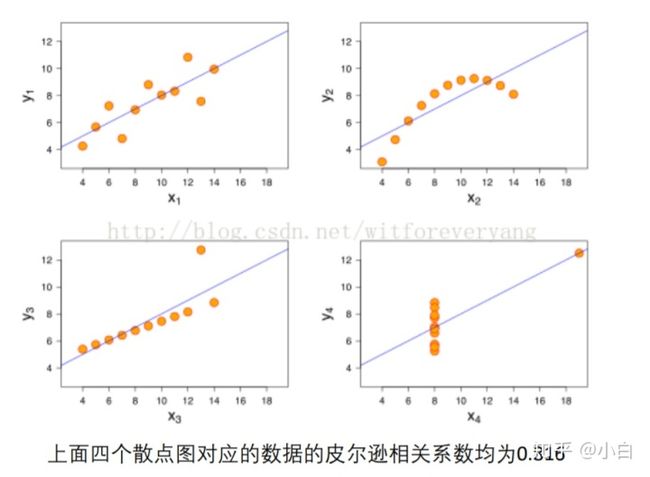
第二点,即使相关系数很大,也不一定真的线性相关。如下图。因此,一定一定一定一定记得画出散点图啊,不要凭借一个相关系数就说它们相关不相关了(血与泪的教训呜呜呜呜呜呜)
举个例子
直接用matlab计算相关系数矩阵就好啦~将数据导入之后,一行代码搞定。
R 结果如下
我们可以在excel中用色阶美化一下,当然如果使用Python或者R语言会有很好用的第三方库或者包直接生成美观的相关系数矩阵。
其实也不是很美,但颜色深浅可以表达出相关系数的大小,很直观。之后有机会我再介绍一下如何用Python或者Excel生成好看的图表。
如果想要计算两个向量的相关系数,也是一行代码搞定。
x唔,结果也是一个矩阵,不过可以直接看出来相关系数啦。
对Pearson相关系数进行假设检验
其实在上统计这门课的时候,印象中我没有见到过对相关系数进行假设检验,更多的是对均值、方差、比例等进行假设检验。不过清风老师的课中提到了这部分,我也就简单介绍一下步骤,具体的原理我觉得还是需要认真学习统计这门课才行。这里不做过多展开。说到这里,大家可以试试在公众号后台发送数学建模文章的名字,有惊喜呀。
首先说一下什么是假设检验。原理其实比较简单:我们假设某个命题是正确的,在这个假设正确的前提下,事件A是一个小概率事件。我们知道,在一次实验中小概率事件几乎不可能发生。所以,如果我们在一次试验中观察到事件A竟然发生了,就有足够的理由怀疑这一假设的正确性,从而否定该假设;反正,如果在一次试验中事件A并没有发生,我们就无法否定原假设,只能转而支持原假设了。(虽然无法否定原假设并不代表原假设就是正确的,但是在假设检验的框架下,我们认为无法否定就要支持)
我们将设为正确的假设,称之为原假设
上面可能就是构造拒绝域那里不太清楚,这里就不讲了,有机会还会提到。一般而言,我们反而不用拒绝域,用的是
也就是说,我们把题目提供的样本,当成一次实验的结果。在
如果这个概率很小,例如只有0.001,大概意味着重复1000次实验,才会出现题目中样本的结果或者比它更极端的结果,那么我们认为小概率事件发生了,需要否定原假设。如果这个概率是0.2,那么100次实验中,有20次都会出现题目中样本的结果甚至更加极端的结果,这并不能算是小概率事件发生了,因此我们无法拒绝原假设,转而需要拒绝备注假设,支持原假设。
啊这部分确实就是比较难理解,如果不太懂也可以看看教科书以及知乎的一些回答,可能某一天就突然懂了。
欧克,针对相关系数的假设检验,我们提出的原假设
之后我们构造统计量,这里构造的是
在然后就是计算
用matlab就简单多了,corrcoef函数不仅可以返回相关系数,还可以返回
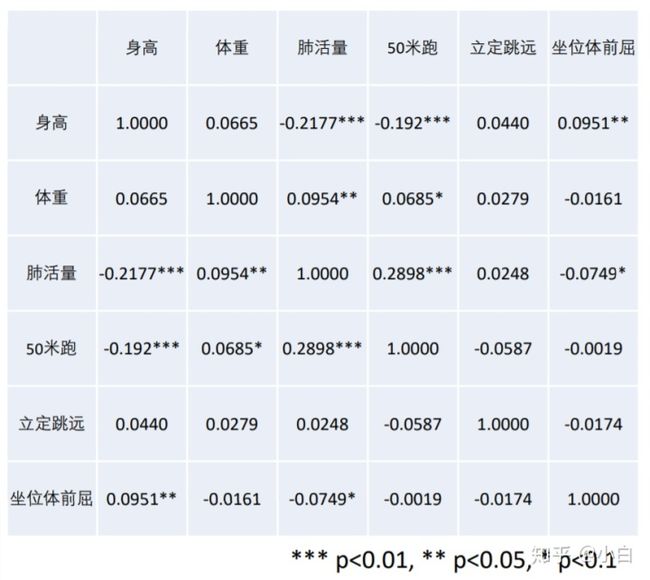
[之后我们在原先的结果上标出相应的显著性水平,标记3颗星的位置,意味着置信水平是99%,标记2颗星的位置,意味着置信水平是95%,标记1颗星的位置,意味着置信水平是95%。显著性水平=1-置信水平,这里代表着相关系数显著为0的显著性。则置信水平越高,显著性越低,越不可能为0。
可以发现,那几个显著不为0的相关系数绝对值都不>0.8,说明这几项指标两两之间并没有明显的线性关系。
事实上,对相关系数进行假设检验,还要求相关的指标变量一定程度上服从正态分布。对于大样本(n>30),我们使用JB检验,原假设是服从正态,备择假设是不服从正态,之后调用matlab的jbtest函数。
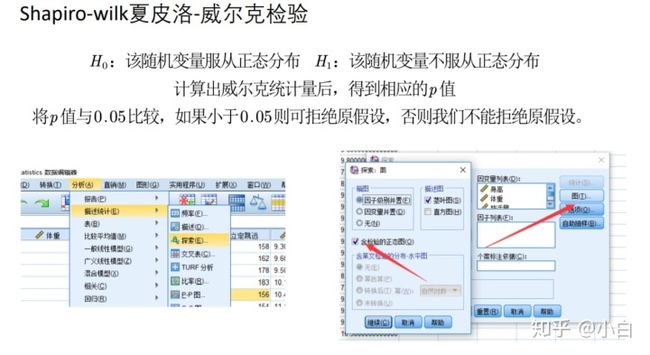
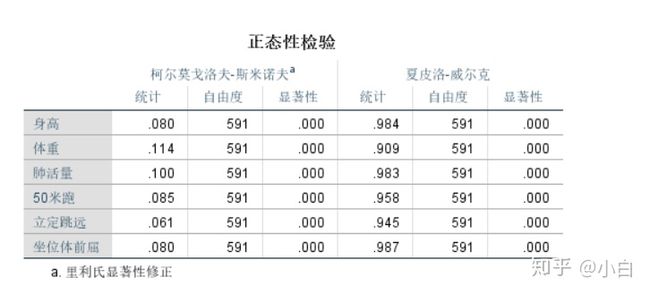
[对于小样本,可以使用
喵这里就先不讲spss的具体操作了,需要录个简单的视频,最近没什么时间。等有空的时候我录屏演示一下。
好的,Pearson相关系数就说到这里。
spearman相关系数
定义
一个数的等级,就是将它所在的一列数按照从小到大排序后,这个数所在的位置,如果有的数值相同,则将它们所在的位置取算术平均。
上述公式就算得到
另一种spearman相关系数,被定义为等级之间的Pearson相关系数,也就是上图中
%% 斯皮尔曼相关系数
spearman相关系数也需要假设检验,原假设也是
% 直接给出相关系数和p值
斯皮尔曼相关系数表明
嗯,spearman相关系数相对而言用的不是特别多,这里不做过多展开。
总结
以上就是相关系数我学到的全部内容啦,到这里已经写了四个小时了……其实是个很简单的话题,认真学也就一小时就大概搞懂了,没想到写起来这么费劲qwq。最后用一张清风老师的课件进行总结吧。如果本文对你有帮助的话,帮忙点个赞呗qwq。