23微分方程和exp(At)

预备知识

1.1 一阶线性微分方程的解

$$\frac{dy}{dx}+P(x)y=Q(x)\text{\hspace{1em}(1)}$$
其齐次通解为：
$$y=C{e}^{-\int P(x)dx}\text{\hspace{1em}(2)}$$
非齐次通解为：
$$y=C{e}^{-\int P(x)dx}+e^{-\int P(x)dx}\int Q(x)e^{\int P(x)dx}dx\text{\hspace{1em}(3)}$$
假设$P(x)=-\lambda$，$\lambda$为常数。对应的解为：
$$\frac{dy}{dx}=\lambda y\text{\hspace{1em}(1)}$$

$$y=C{e}^{-\lambda x}\text{\hspace{1em}(4)}$$
特别的，$\lambda =0$，有：$y=C$

1.2 欧拉公式

$$e^{i\theta }=\cos \theta +i\sin \theta \text{\hspace{1em}(5)}$$
对于任意一个角度，欧拉公式给出了单位圆上唯一的复数，请注意不是一一对应，因为对于任意$\theta +2k\pi$都表示同一个复数。需要留意的是 $e^{a+bi}$的模为：
$$e^{a+bi}=e^a{e}^{bi}=|e^a||e^{bi}|$$
复数部分，套用欧拉公式有：
$$|e^{bi}|=|\cos b+i\sin b|={\cos }^{2}b+{\sin }^{2}b=1$$
结论就是：e的复数指数的模长等于实数部分的数值。

一、常系数微分方程组

不考虑耦合情况，求解以下微分方程是容易的：（这里的常系数指的是$y$及其导数对应的系数为一个常数，而不是带有未知数、可以变化的）
$$\frac{du}{dt}=u\frac{du}{dt}=\lambda u\text{\hspace{1em}(6)}$$
其实就是一阶线性微分方程，$P(x)=\lambda$和$Q(x)=0$的特殊情况，表达式见（1）。解分别是：
$$u(t)=C{e}^{t}u(t)=C{e}^{\lambda t}\text{\hspace{1em}(7)}$$
假如，两个微分方程组相互耦合，那么应该如何求解其微分方程组的解？看一个具体的例子：

$$\begin{array}{rl}\frac{d{u}_1}{dt}& =-u_1+2u_2\\ \frac{d{u}_2}{dt}& =u_1-2u_2\end{array}\text{\hspace{1em}(8)}$$
如何求解？两个方程相加有：
$$\frac{d(u_1+u_2)}{dt}=0(u_1+u_2)\text{\hspace{1em}(9)}$$
上式减去两倍的下式，有：
$$\frac{d(u_1-2u_2)}{dt}=-3(u_1-2u_2)\text{\hspace{1em}(10)}$$
将$u_1+u_2$看成一个整体，方程(9)对应的微分方程的解为
$$u_1+u_2=C_1{e}^{0t}\text{\hspace{1em}(11)}$$
同样，将$u_1-2u_2$看成一个整体有：
$$u_1-2u_2=C_2{e}^{-3t}\text{\hspace{1em}(12)}$$
进行一些简单的消元操作，可以得到微分方程组的解：
$$\begin{array}{r}{u}_1=\frac{2C_1}{3}{e}^{0t}+\frac{C_2}{3}{e}^{-3t}\\ u_2=\frac{C_1}{3}{e}^{0t}-\frac{C_2}{3}{e}^{-3t}\end{array}\text{\hspace{1em}(13)}$$
至此，微分方程组求解完毕。从求解过程可以看出：

• 求解一阶常系数微分方程组的基本方法就是通过线性变换右侧，使得左侧微分对象恰好等于组合的结果；
• 微分方程组的解是多个$e^{\lambda }t$组成的，也就是$u_i=\sum C_i{e}^{{\lambda }_{i}t}{x}_i$；[1]

这个和矩阵有何关系？或许写成矩阵更加容易看出一些端倪：
$$\frac{d}{dt}\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right]=\left[\begin{array}{cc}-1& 2\\ 1& -2\end{array}\right]\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right]\text{\hspace{1em}(14)}$$
我们微分方程组的解$u_1$和$u_2$看成未知数列向量：$x=\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right]$，右侧的系数组合看成是系数矩阵$A=\left[\begin{array}{cc}-1& 2\\ 1& -2\end{array}\right]$。一个矩阵作用于一个向量大概率会改变这个向量的方向，我们的目标是通过线性变换，这和将方程式左边的向量变成是与之同方向的向量是一样的，一旦能写成同方向的向量，这个方程就是一个容易求解的一阶线性微分方程。

啰里啰唆，其实就是想说明：我们可以利用特征值和特征向量的概念来求解微分方程组。下面来看看这个微分方程组是如何通过特征值和特征向量求解的。令
$$A=\left[\begin{array}{cc}-1& 2\\ 1& -2\end{array}\right]\text{\hspace{1em}(15)}$$
容易求得其特征值：${\lambda }_1=0$ ${\lambda }_2=-3$，对应的特征向量为:$x_1=\left[\begin{array}{c}2\\ 1\end{array}\right]$和$x_2=\left[\begin{array}{c}1\\ -1\end{array}\right]$，根据通解公式有：
$$u(t)=C_1{e}^{0t}\left[\begin{array}{c}2\\ 1\end{array}\right]+C_2{e}^{-3t}\left[\begin{array}{c}1\\ -1\end{array}\right]$$
如果给定初值：$u_0=\left[\begin{array}{c}1\\ 0\end{array}\right]$，可以确定$C_1$和$C_2$的具体数值。最终的解为：
$$u(t)=\frac{1}{3}{e}^{0t}\left[\begin{array}{c}2\\ 1\end{array}\right]+\frac{1}{3}{e}^{-3t}\left[\begin{array}{c}1\\ -1\end{array}\right]$$

也就是：
$$\begin{gathered} u_1(t)=\frac{2}{3}{e}^{0t}+\frac{1}{3}{e}^{-3t} \\ {u}_2(t)=\frac{1}{3}{e}^{0t}-\frac{1}{3}{e}^{-3t} \end{gathered}$$
微分方程的两个解的趋势如何？

• 如果特征值为0，那么该分量是一个定值与时间无关；
• 如果特征值为负实数，随着时间的推移，该分量将会趋近于0；
• 如果特征值为正实数，随着时间的推移，该分量将会变得无穷大；
• 如果特征值为负数，只需要看实数部分正负即可，同23点，复数部分只是在指明方向，一直在单位圆上转圈圈；

最后讲一下解的稳定性问题：

• 稳定性（stability）。如果定义 $u(t)\to 0$为稳定状态，那么特征值应该满足什么条件？答：实数部分都小于零；(模是收敛的)
• 稳态（steady state）。存在一个特征值为0，其他特征值实部小于0；
• 震荡（blow up）。如果存在任意特征值实属部分大于零。

对于一个$2\times 2$矩阵$A=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$的稳定性条件是什么？
答：根据之前的讨论，矩阵需要满足稳定的条件是：$Re{\lambda }_1<0$ $Re{\lambda }_2<0$。如果不计算特征值，我们是否可判断这个矩阵的稳定性？

• 迹 （trace）小于零。 $a+d={\lambda }_1+{\lambda }_2<0$
• 行列式（determinant）的值大于0 ${\lambda }_1{\lambda }_2>0$

二、e的矩阵次方

回到原来的方程：
$$\frac{du}{dt}=Au$$
我们的目的是将方程组$u$解耦，不妨设 $u=Sv$，其中$S$为矩阵$A$特征向量构成的特征矩阵。（将 $u$ $v$想象向量，因为 $S$是特征向量矩阵，故一定是线性无关，所以一定存在$v$使得$u=Sv$成立）。将条件$u=Sv$带入方程有：
$$S\frac{dv}{dt}=ASv$$
将$S$移到右边有：
$$\frac{dv}{dt}=S^{-1}ASv=\Lambda v$$
为什么我们要大费周折的将一个方程式化简成对角矩阵？答案就是解耦，一旦系数矩阵变成了对角矩阵，微分方程之间的耦合将不再存在！不存在耦合求解微分方程简直不要太常规：
$$\begin{gathered} v_1=c_1{e}^{{\lambda }_{1}t} \\ {v}_2=c_2{e}^{{\lambda }_{2}t} \\ \cdots \end{gathered}$$
或者你不想这么啰嗦，直接用矩阵表示：
$$\begin{gathered} u(t)=e^{\Lambda t}v(0) \\ u(t)=S{e}^{\Lambda t}{S}^{-1}u(0) \end{gathered}$$
下面直接给出一个结论以简化 $u(t)$：
$$e^{At}=S{e}^{\Lambda t}{S}^{-1}$$
在此之前我们的指数都是针对于一个具体的数，在这里出现的$e$的矩阵次幂是什么含义？在此之前我们需要先给定矩阵指数的概念：

矩阵指数定义如下：
$$e^{At}=I+At+\frac{(At{)}^2}{2}+\frac{(At{)}^3}{6}+\cdots +\frac{(At{)}^n}{n!}$$
上述的展开是收敛的，因为随着$n$的增大，通项收敛于0；

这与高等数学里的$e^x$对应： $$e^x=\sum _{n=0}^{\infty }\frac{x^n}{n!}$$
利用高数极限的定义可证，当$n\to +\infty$时，$e^x\to 0$。
(几何级数)：
$$\frac{1}{1-x}=\sum _{n=0}^{\infty }{X}^n$$

类比几何级数有：
$$(I-At{)}^{-1}=I+At+A{t}^2+\cdots$$
这个性质可用来估计矩阵的逆，当$t$比较小的时候，高阶项可以忽略。这个式子不一定收敛，收敛条件是 $At$的特征值小于1，求逆公式成立。

利用 $e^{At}$的定义，我们来推导当满足$A$可对角化情况下的表达式：
$$\begin{array}{rl}{e}^{At}& =I+At+\frac{(At{)}^2}{2}+\frac{(At{)}^3}{6}+\cdots +\frac{(At{)}^n}{n!}\\ & =S{\Lambda }^0{S}^{-1}+S{\Lambda }^1{S}^{-1}t+\frac{1}{2!}S{\Lambda }^2{S}^{-1}{t}^2+\cdots +\frac{1}{n!}S{\Lambda }^n{S}^{-1}{t}^n\\ & =S(I+\Lambda t+\frac{1}{2!}{\Lambda }^2{t}^2+\frac{1}{3!}{\Lambda }^3{t}^3+\cdots +\frac{1}{n!}{\Lambda }^n{t}^n)S^{-1}\\ & =S{e}^{\Lambda t}{S}^{-1}\end{array}$$
特征值构成的矩阵$\Lambda$：
$$\Lambda =\left[\begin{array}{cccc}{\lambda }_1& 0& \cdots & 0\\ 0& {\lambda }_2& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\lambda }_n\end{array}\right]$$
回到一开始的$v(t)=e^{\Lambda t}v(0)$，因为已经解耦，所以每一列都代表了对应解的形式，故：
$$e^{\Lambda t}=\left[\begin{array}{cccc}{e}^{{\lambda }_{1}t}& 0& \cdots & 0\\ 0& e^{{\lambda }_{2}t}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & e^{{\lambda }_{n}t}\end{array}\right]$$
对于，考察$u(t)$
$$\begin{array}{rl}u(t)& =e^{At}u(0)\\ & =\left[\begin{array}{cccc}{x}_1& x_2& \cdots & x_n\end{array}\right]\left[\begin{array}{cccc}{e}^{{\lambda }_{1}t}& 0& \cdots & 0\\ 0& e^{{\lambda }_{2}t}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & e^{{\lambda }_{n}t}\end{array}\right]\left[\begin{array}{c}{c}_1\\ c_2\\ ⋮\\ c_n\end{array}\right]\\ & =c_1{x}_1{e}^{{\lambda }_{1}t}+c_2{x}_2{e}^{{\lambda }_{2}t}+\cdots +c_n{x}_n{e}^{{\lambda }_{n}t}\end{array}$$
这个与我们认识的通解形式是一致的。

怎么样的特征值会使得微分方程有稳定解？
答：根据稳定性的定义，当微分方程的表达式趋于0时，微分方程具有稳定解。
$$u(t)=S{e}^{\Lambda t}{S}^{-1}u(0)$$
表达式$S$和$S^{-1}$不变，趋势和$e^{\Lambda t}$有关：
$$e^{\Lambda t}=\left[\begin{array}{cccc}{e}^{{\lambda }_{1}t}& 0& \cdots & 0\\ 0& e^{{\lambda }_{2}t}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & e^{{\lambda }_{n}t}\end{array}\right]$$
当且仅当，所有特征根都小于零时，微分方程的结果随着时间的增大会趋于一个稳定的值：0。在复平面上标记特征根，他应该出现在复平面的左半部分：

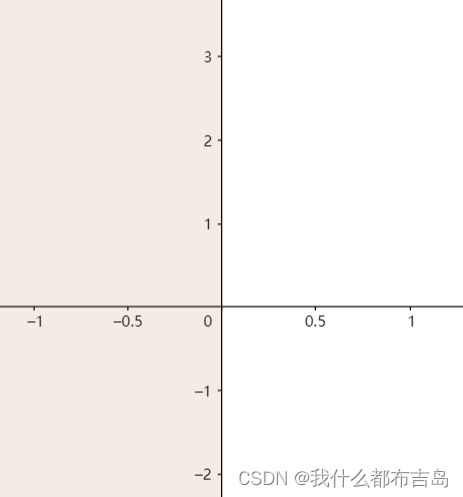
三、高阶常系数微分方程

对于一个二阶微分方程：
$$y^{\prime \prime }+b{y}^{\prime }+ky=0$$
一个常用的技巧就是降阶：
$$u=\left[\begin{array}{c}{y}^{\prime }\\ y\end{array}\right]$$
于是，二阶方程可以写成：
$$u^{\prime }=\left[\begin{array}{c}{y}^{\prime \prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}-b& -k\\ 1& 0\end{array}\right]\left[\begin{array}{c}{y}^{\prime }\\ y\end{array}\right]$$
也就是
$$u^{\prime }=Au$$
解法和前面讲到的一样，不过$u$内容变成了解的各阶导数。

同理，如果是五阶微分方程，亦可用同样的方法。

---

[1] 没有看到详细的推导。
[2] https://blog.csdn.net/sunbobosun56801/article/details/103094021