Matlab自适应滤波算法 LMS小白通俗易懂版

Matlab自适应滤波算法

在学习自适应算法的过程中，入门阶段，学习了LMS,NLMS，符号LMS算法，并用Matlab对算法进行了复现，复现的内容主要包括，算法主体部分。

LMS

最小均方LMS是一种搜索算法，它通过对目标函数进行适当修改，以便简化梯度向量的计算，由于其计算简单，LMS算法及与之相关的其他算法，已经广泛应用于自适应滤波的各种的应用中。

先写一下官方给的算法公式

---

$Initialize:$
$x(0)=w(0)=[000\cdot \cdot \cdot \cdot \cdot 000{]}^T$

$fori=1:k$
$e(k)=d(k)-x^T(k)w(k)$
$w(k+1)=w(k)+2\mu e(k)x(k)$
$end$

---

介绍算法变量

注意$x$不是原信号，$x$是来自于原信号中与权重长度一致的与权重进行运算的数据

$w$为权重，首先需要对输入信号和权重进行初始化
$x(0)=w(0)=[000\cdot \cdot \cdot \cdot \cdot 000{]}^T$
$k$是迭代次数
$d(k)$为期望信号的第$k$个值
$e$是存储每一次迭代误差的一个向量，$e(k)$为第k次迭代的理想信号与经过滤波器（输入信号与权重相乘）的输入信号的结果做差
$e(k)=d(k)-x^T(k)w(k)$
计算出对应的迭代误差后，使用该误差结合一个更新步长$\mu$对权重进行更新
$w(k+1)=w(k)+2\mu e(k)x(k)$

梳理完算法的结构对算法进行复现

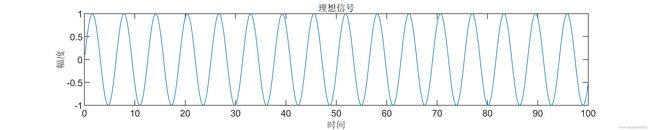
• 第一步生成一个理想信号

t = 0.1:0.1:100; %时间轴
signal_len = length(t);%信号长度
d = sin(t);%理想信号
plot(t,d)
xlabel('时间')
ylabel('幅度')
title('理想信号')

• 第二步生成一个随机高斯白噪声

t = 0.1:0.1:100; %时间轴
noise = 0.1*randn(1,signal_len);%噪声

plot(t,noise)
xlabel('时间')
ylabel('幅度')
title('噪声')

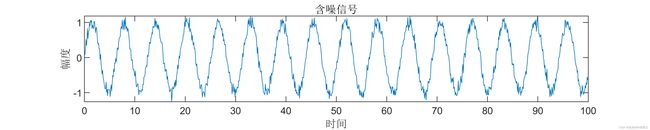
• 第三步生成含有噪声的信号

t = 0.1:0.1:100; %时间轴
signal_len = length(t);%信号长度
d = sin(t);%理想信号

noise = 0.1*randn(1,signal_len);%噪声
d_noise =  d+noise;%要过滤的信号-加了噪声的信号

plot(t,d_nosie)
xlabel('时间')
ylabel('幅度')
title('含噪信号')

• 第三步初始化需要的变量

filter_len = 50;  %滤波器长度
W = zeros(1,filter_len); %初始化滤波器
x = zeros(1,filter_len); %初始化卷积输入
After_filter = zeros(1,signal_len);%用于存储滤波之后的信号
e = zeros(1,signal_len); %初始化误差
mull = 0.03; %步长

除了算法公式中给到的$x$和$w$之外还要定义一个训练步长以及滤波器长度，以及存储误差的变量。

• 第四步编写算法主体

for k =1:signal_len
    x = [d_noise(k) x(1:filter_len-1)]; %线性卷积的输入
    After_filter(k) = W*x';
    e(k) =d(k) - After_filter(k);%计算误差
    W = W + 2*mull*e(k)*x; %计算误差更新权重
end

解释一下改句的运行原理，LMS算法中的输入信号实际上是用于和滤波器也就是权重进行卷积的信号需要将理想信号中的数据进行部分截取然后再翻转

 x = [d_noise(k) x(1:filter_len-1)]; %线性卷积的输入

这里先介绍一下Matlab的合并语法，如果将两个向量间隔一个空格放到一个中括号里实际上就是对这两个数据在横向上进行拼接。

然后模拟一下线性卷积的输入循环，下图展示了改代码机制是如果对原信号进行边位移边反转还能截取固定长度的功能，这块要是不清楚的话，可以去看下卷积的原理。

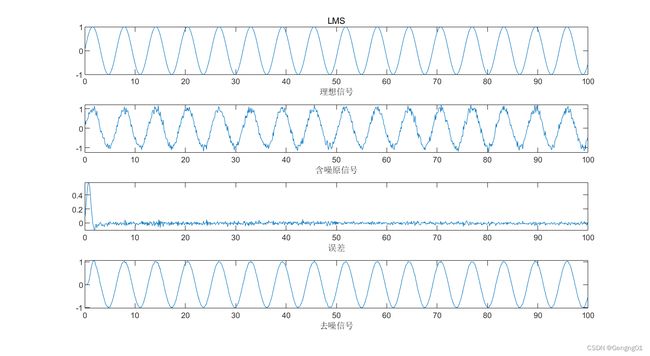
• 第五步绘图
  将理想信号含噪信号误差信号以及去噪信号放到一起进行输出

subplot(411)
plot(d)
title('LMS')
xlabel('理想信号')

subplot(412)
plot(d_noise)
xlabel('含噪原信号')

subplot(413)
plot(e)
xlabel('误差')

subplot(414)
plot(After_filter)
xlabel('去噪信号')

完整代码

clc;%清除工作区
clear;%清除命令窗口

t = 0.1:0.1:100; %时间轴
signal_len = length(t);%信号长度
d = sin(t);%理想信号

noise = 0.1*randn(1,signal_len);%噪声
d_noise =  d+noise;%要过滤的信号-加了噪声的信号

filter_len = 50;  %滤波器长度
W = zeros(1,filter_len); %初始化滤波器
x = zeros(1,filter_len); %初始化卷积输入
After_filter = zeros(1,signal_len);%用于存储滤波之后的信号
e = zeros(1,signal_len); %初始化误差
mull = 0.03; %步长


for k =1:signal_len
    x = [d_noise(k) x(1:filter_len-1)]; %线性卷积的输入
    After_filter(k) = W*x';
    e(k) =d(k) - After_filter(k);%计算误差
    W = W + 2*mull*e(k)*x; %计算误差更新权重
end

figure(1)
subplot(411)
plot(t,d)
title('LMS')
xlabel('理想信号')

subplot(412)
plot(t,d_noise)
xlabel('含噪原信号')

subplot(413)
plot(t,e)
xlabel('误差')

subplot(414)
plot(t,After_filter)
xlabel('去噪信号')

总结

在论文对比中需要用到MSE指标等，并需要进行蒙特卡洛实验，下一步继续更新NLMS和符号LMS算法。