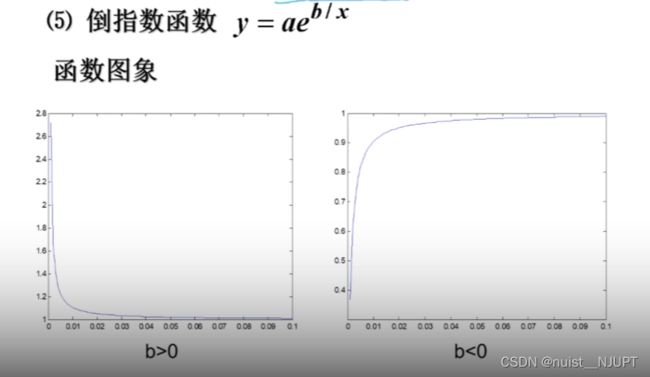
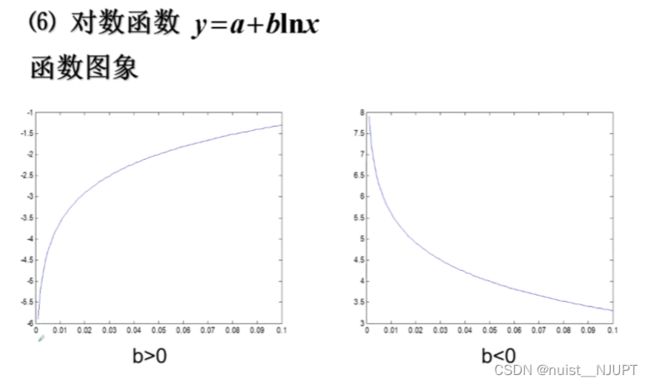
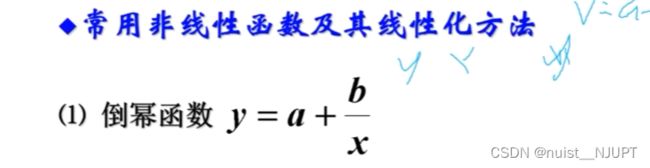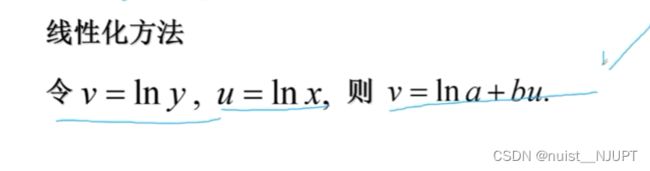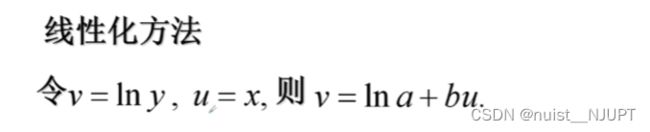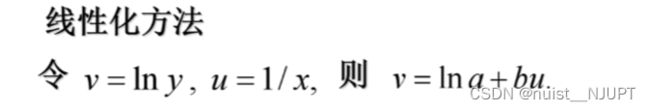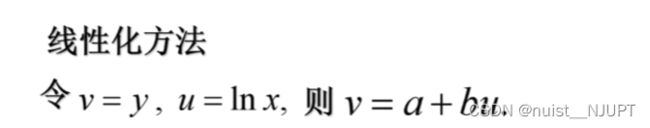备战数学建模17-回归分析算法
目录
一、一元线性回归
1-一元线性回归及最小二乘法
2-回归方程的显著性检验
3-回归系数的置信区间
4-预测与控制
5-可线性化的一元非线性回归(曲线回归)
二、多元线性回归
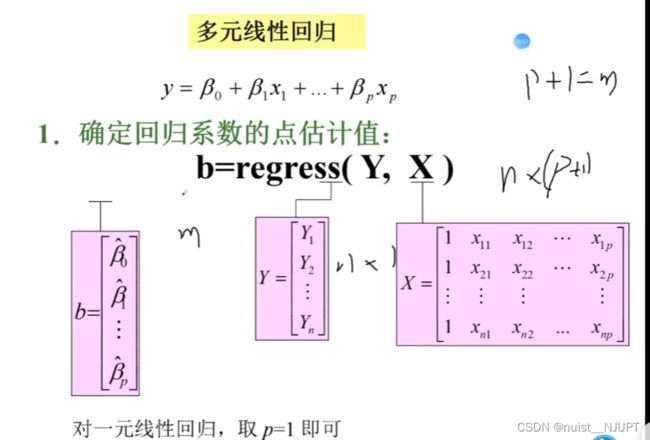
1-多元线性回归相关理论
2-多元线性回归的MATLAB编程实现
3-非线性回归的MATLAB编程实现
4-逐步回归的MATLAB编程实现
一、一元线性回归
1-一元线性回归及最小二乘法
我们下面需要一下最小二乘法，使得误差Q最小，具体如下：
普通的最小二乘法，适用于连续的函数，因为要求导。
对于离散形式的数据，也可以使用最小二乘法，具体如下所示：
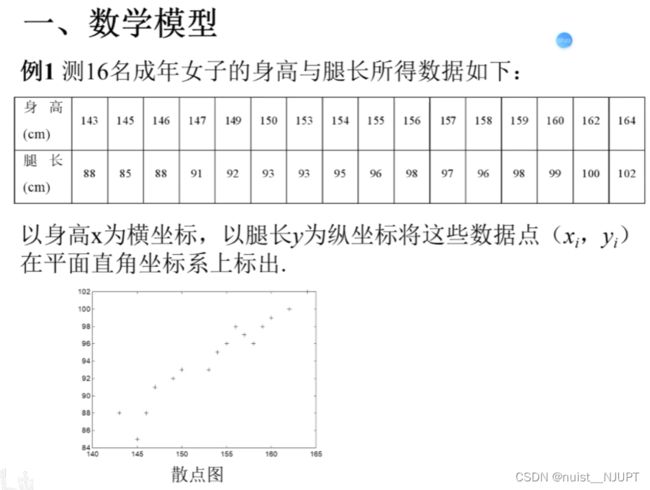
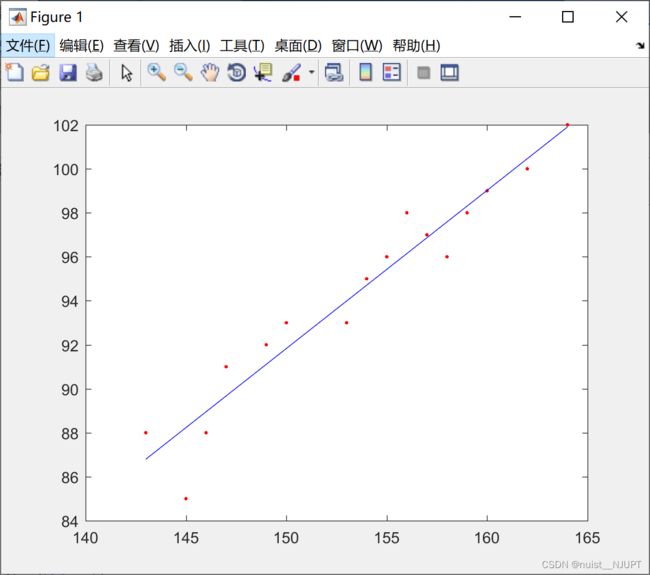
我们看下上面的女生身高与腿长的数据，在MATLAB中绘制散点图，代码如下，可以发现身高与腿长近似是线性关系，我们可以假设成一元线性回归模型：y = b0 + b1x ;然后根据根据最小二乘法求出b0,b1,绘制拟合曲线。
最小二乘法参数估计及一次多项式拟合代码如下所示：
clear; clc
x = [143, 145, 146, 147, 149, 150, 153, 154, 155, 156, 157, 158, 159, 160, 162, 164] ;
y = [88, 85, 88, 91, 92, 93, 93, 95, 96, 98, 97, 96, 98, 99, 100, 102] ;
n = length(x) ;
Y = y' ;
X = [ones(n,1),x'] ;
plot(x, y, '.r') ; %绘制散点图
hold on ;
x_bar = mean(x) ;
y_bar = mean(y) ;
sum1 = 0 ;
sum2 = 0 ;
for i = 1 : n
sum1 = sum1 + x(i) * x(i) ;
sum2 = sum2 + x(i) * y(i) ;
end
Lxx = sum1 - n * (x_bar)^2 ;
Lxy = sum2 - n * x_bar * y_bar ;
b1 = Lxy / Lxx ;
b0 = y_bar - b1*x_bar ;
disp('b0 = ') ;
disp(b0) ;
disp('b1 = ') ;
disp(b1) ;
p = polyfit(x,y,1) ; %一次多项式拟合
disp('b1和b0如下：') ;
disp(p) ;
plot(x,polyval(p,x),'b') ;运行结果如下：
2-回归方程的显著性检验
显著性水平：即犯错的概率，犯错的概率越低越好。
下面我们学习一下具体的三种检验方法，具体如下所示：
拒绝原假设，则说明回归方程有意义，否则，认为回归方程不合理。
t检验适用于整体样本较少的检验，若样本数n<30,可以考虑t检验。拒绝原假设，则回归比较合适。
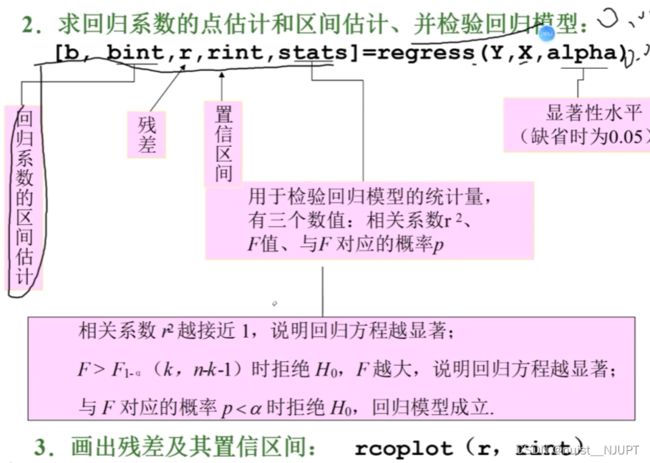
3-回归系数的置信区间
4-预测与控制
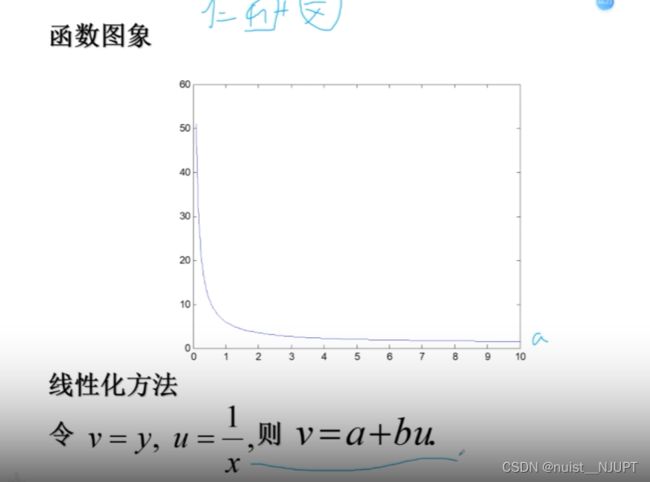
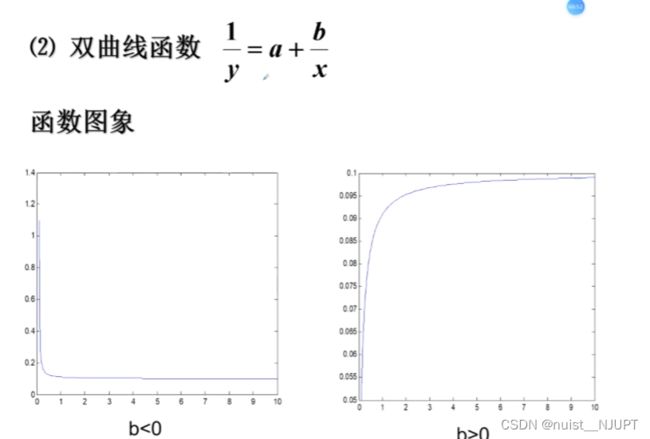
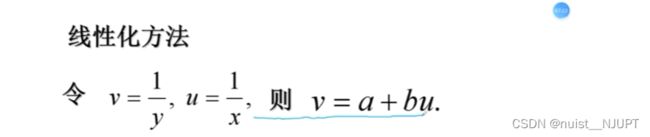
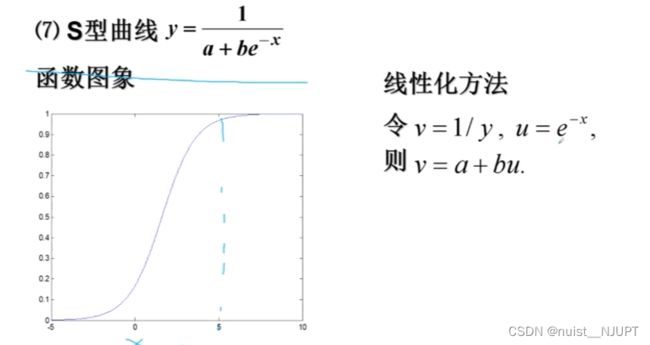
5-可线性化的一元非线性回归(曲线回归)
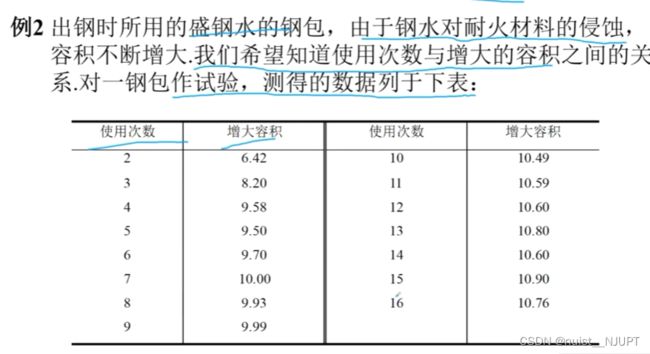
我们看下面的例子2，一元非线性回归的例子具体如下：
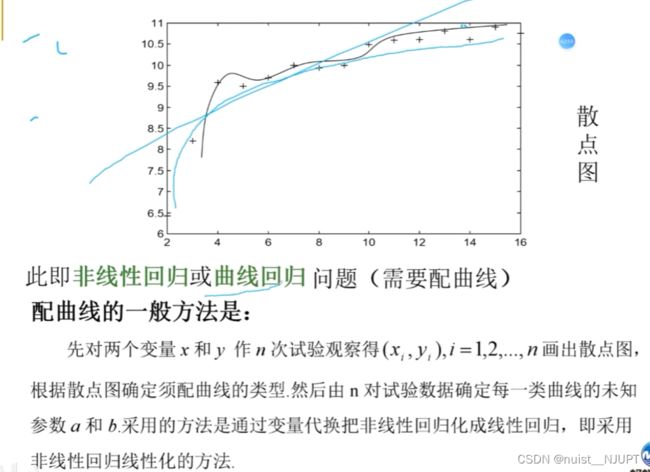
对于上述的钢包使用次数和增大容积的例题，明显根据散点图发现是非线性回归模型，根据散点图确定曲线类型，计算出a,b，通过非线性转换为线性的方法。
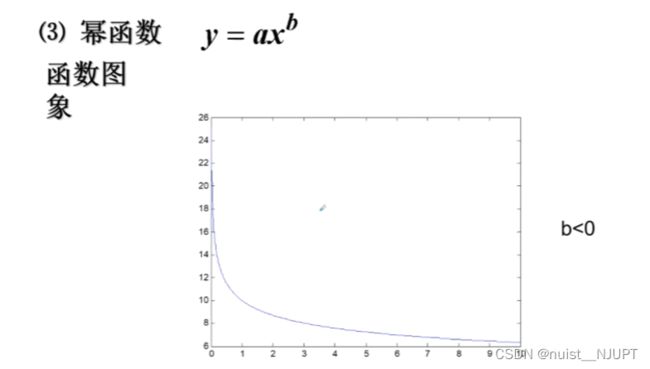
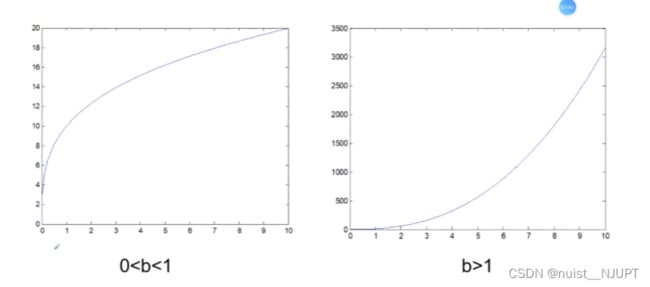
看着散点图和幂函数很像，转化成线性函数y = a * x^b
令v = Iny , u = Inx , v = Ina + bu ;
具体的MATLAB求解代码如下所示：
clear; clc
x = 2 : 16 ;
y = [6.42, 8.2, 9.58, 9.5, 9.7, 10, 9.93, 9.99, 10.49, 10.59, 10.6, 10.8, 10.6, 10.9, 10.76] ;
X = [ones(15,1), (log(x))'] ;
Y = (log(y))' ;
b = regress(Y,X) ;
disp('系数如下：') ;
disp(b) ;
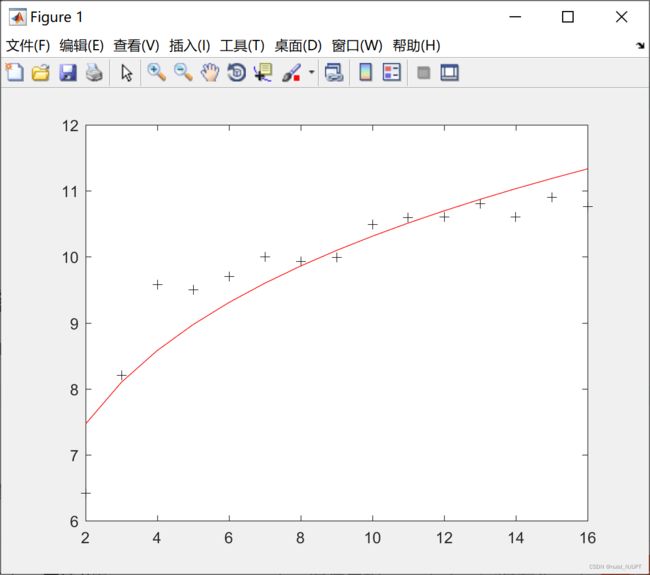
z = 6.4961 * (x.^0.2007) ;
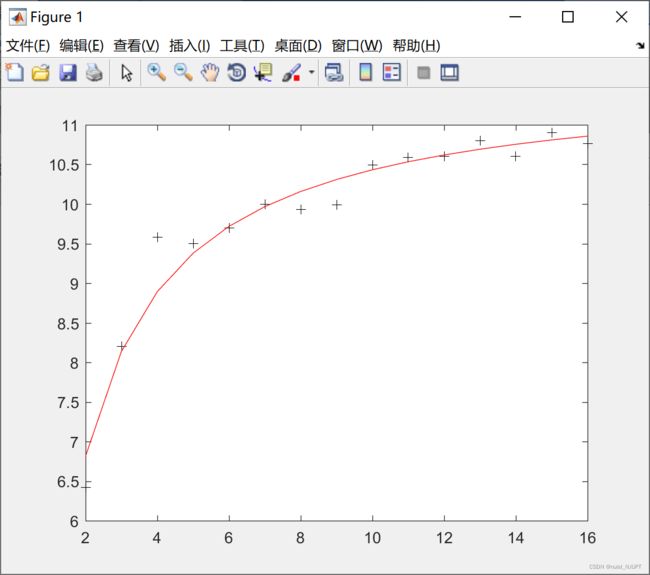
plot(x,y,'k+',x,z,'r') ;运行结果如下，这求出来的是Ina和b，需要还原成原来的函数。Ina=1.8712,a=6.4961.
最终的方程是：y = 6.4961 * (x^0.2007),预测曲线如下：
二、多元线性回归
1-多元线性回归相关理论
2-多元线性回归的MATLAB编程实现
对于上述多元线性回归，这边将完整的MATLAB代码给出：
clear; clc
clear; clc
x = [143, 145, 146, 147, 149, 150, 153, 154, 155, 156, 157, 158, 159, 160, 162, 164] ;
y = [88, 85, 88, 91, 92, 93, 93, 95, 96, 98, 97, 96, 98, 99, 100, 102] ;
n = length(x) ;
Y = y' ;
X = [ones(n,1),x'] ;
[b,bint,r,rint,stats] = regress(Y,X) ;
disp('回归系数如下：') ;
disp(b) ;
disp('回归系数的区间估计如下：') ;
disp(bint) ;
disp('相关系数、F、概率p分别如下：') ;
disp(stats) ;
subplot(1,2,1) ;
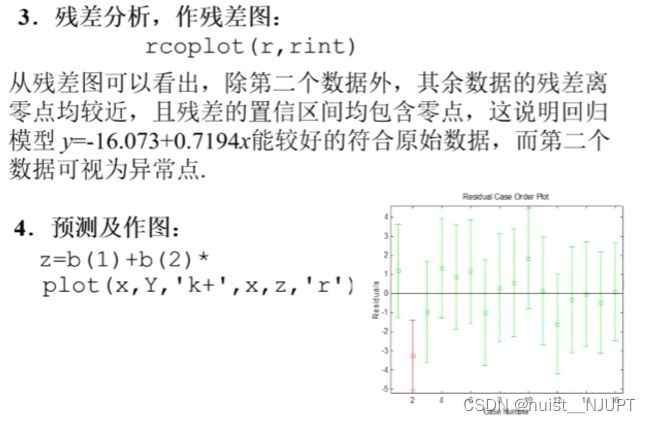
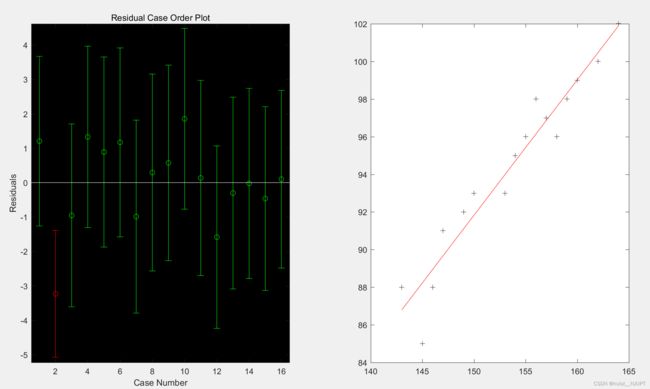
rcoplot(r, rint) ; %做残差图
subplot(1,2,2) ;
z = b(1) + b(2) * x ;
plot(x,y,'k+',x,z,'r') ;运行结果如下所示，相关系数接近1，回归显著，p<0.05,拒绝原假设，模型成立，根据残差图发现第2个点不理想，其余数据的参照均靠近0点，故模型能较好的符合原始数据，第2个点视为异常点，回归模型成立。
一元二次多项式回归的MATLAB代码这边给出，方法一直接二次多项式回归，具体如下：
clear; clc
t = 1/30 : 1/30 : 14/30;
s = [11.86, 15.67, 20.6, 26.69, 33.71, 41.93, 51.13, 61.49, 72.9, 85.44, 99.08, 113.77, 129.54, 146.48] ;
[p,S] = polyfit(t,s,2) ; %二次多项式拟合
disp('回归系数如下：') ;
disp(p) ;
y = polyval(p, t) ;
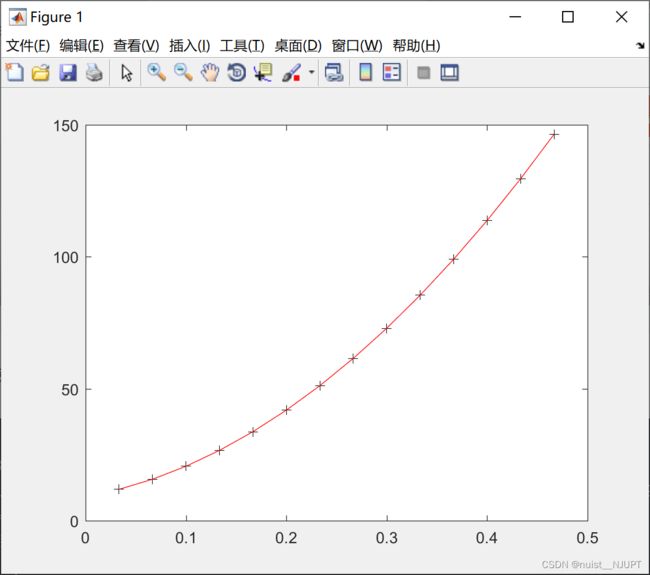
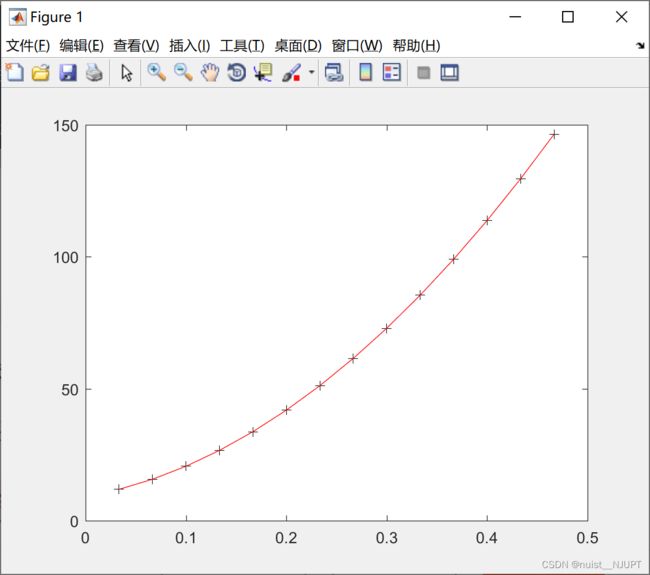
plot(t,s,'k+',t,y,'r') ;运行结果如下所示：
将一元二次的多项式回归转换为多项式回归，进行模型求解和预测，具体MATLAB代码如下：
clear; clc
t = 1/30 : 1/30 : 14/30;
s = [11.86, 15.67, 20.6, 26.69, 33.71, 41.93, 51.13, 61.49, 72.9, 85.44, 99.08, 113.77, 129.54, 146.48] ;
T = [ones(14,1), t', (t.^2)'] ;
[b, bint, r, rint, stats] = regress(s', T) ;
disp('回归系数如下：') ;
disp(b) ;
z = b(1) + b(2).*t + b(3).*t.*t ;
plot(t,s,'k+',t,z,'r') ;运行的结果如下，和直接使用多项式拟合得到的结果保持一致的。
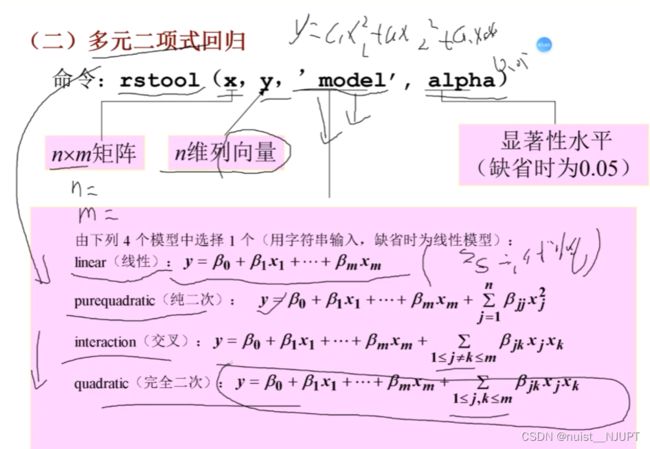
上述多元多项式回归的MATLAB代码如下，对于方法一，直接进行多元二项式回归。
clear; clc
x1 = [1000, 600, 1200, 500, 300, 400, 1300, 1100, 1300, 300] ;
x2 = [5, 7, 6, 6, 8, 7, 5, 4, 3, 9] ;
y = [100, 75, 80, 70, 50, 65, 90, 100, 110, 60] ;
y = y' ;
x = [x1', x2'] ;
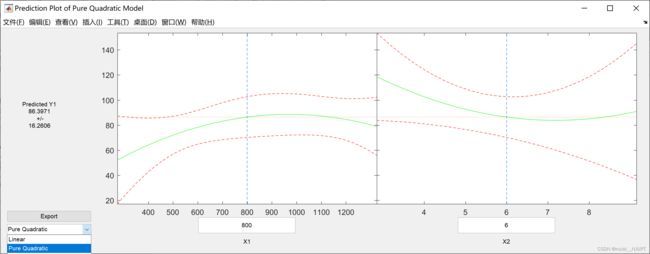
rstool(x, y, 'purequadratic') ;运行结果如下，可以在左下方选择回归模型类型。
选择左下角Export，可以将结果导出，到处后，在命令窗口检验结果：
上述多元多项式回归转换为多元线性回归，即方法二，MATLAB代码如下所示：
clear; clc
x1 = [1000, 600, 1200, 500, 300, 400, 1300, 1100, 1300, 300] ;
x2 = [5, 7, 6, 6, 8, 7, 5, 4, 3, 9] ;
y = [100, 75, 80, 70, 50, 65, 90, 100, 110, 60] ;
y = y' ;
x = [x1', x2'] ;
X = [ones(10,1), x1', x2', (x1.^2)', (x2.^2)'] ;
[b, bint, r, rint, stats] = regress(y,X) ;
disp('多元线性回归方程系数：') ;
disp(b) ;
运行结果具体如下所示：
3-非线性回归的MATLAB编程实现
上述的非线性回归模型的MATLAB代码实现如下，具体如下：
非线性函数volum.m：
function yhat = volum(beta, x)
yhat = beta(1) * exp(beta(2) ./ x) ;
end
主程序如下：
clear; clc
x = 2 : 16 ;
y = [6.42, 8.2, 9.58, 9.5, 9.7, 10, 9.93, 9.99, 10.49, 10.59, 10.6, 10.8, 10.6, 10.9, 10.76] ;
beta0 = [8,2]' ;
[beta, r, J] = nlinfit(x', y', 'volum', beta0) ;
disp('回归系数如下：') ;
disp(beta) ;
[YY, delta] = nlpredci('volum', x', beta, r, J) ;
plot(x,y,'k+', x, YY, 'r') ;运行结果如下所示：
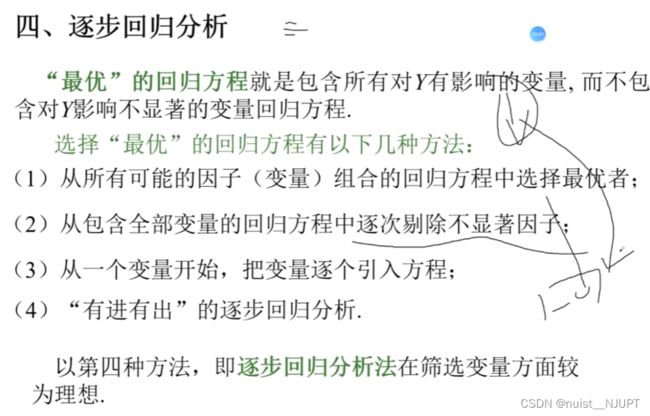
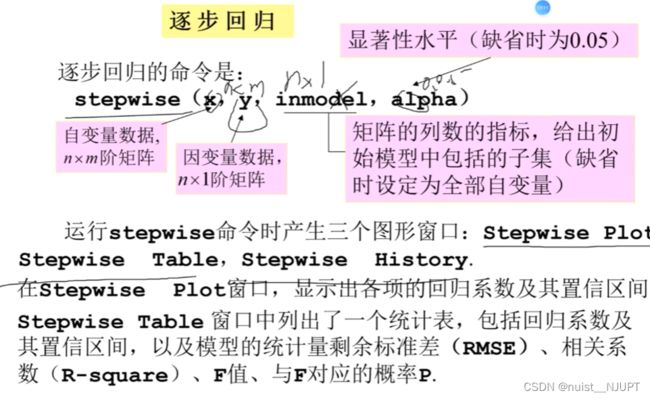
4-逐步回归的MATLAB编程实现
主程序如下：
clear; clc
x1 = [7, 1, 11, 11, 7, 11, 3, 1, 2, 21, 1, 11, 10]' ;
x2 = [26, 29, 56, 31, 52, 55, 71, 31, 54, 47, 40, 66, 68]' ;
x3 = [6, 15, 8, 8, 6, 9, 17, 22, 18, 4, 23, 9, 8]' ;
x4 = [60, 52, 20, 47, 33, 22, 6, 44, 22, 26, 34, 12, 12]' ;
y = [78.5, 74.3, 104.3, 87.6, 95.9, 109.2, 102.7, 72.5, 93.1, 115.9, 83.8, 113.3, 109.4]' ;
x = [x1, x2, x3, x4] ;
stepwise(x, y) ;
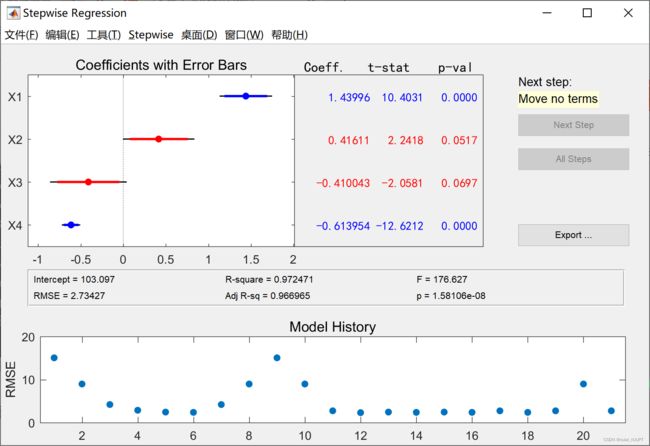
运行结果图如下：
手动移除变量，观察相关性R-square，越接近1越好，RMSE越小越好。如果用四个变量建立回归模型，发现四个变量的相关性为0，所以我们需要手动移除变量，实现逐步回归，保证变量尽可能多的情况下，相关性更高，误差更小。
我们发现把x1和x4移除，变量相关性更高，误差更小，则回归方程更好。
用Export输出所有的参数，在命令窗口输入以下命令求解。
X = [ones(13,1), x2, x3] ;
b = regress(y,X)
得到结果：y = 72.0747 + 0.7313*x2 -1.0084*x3
回归分析的步骤总结一下吧：
1）确定回归方程类型，建立回归模型；
2）求解回归方程，即模型的参数估计；
3）回归方程的显著性检验；
4）利用回归值进行预测与控制；