[论文]A Link-Based Approach to the Cluster Ensemble Problem
论文作者:Natthakan Iam-On, Tossapon Boongoen, Simon Garrett, and Chris Price
下次还是在汇报前先写了论文总结,不然有些点汇报时容易忘了说,以前看的论文看补不补上来吧,有时间再说。
前言:
这篇论文是关于聚类集成的,成熟的聚类集成框架是将多个聚类算法的结果汇聚在一起,然后使用一致性函数得出最终的聚类结果,论文中认为这两步中间的操作属于原数据上的操作,比较粗糙,所以提出了一种算法,对汇总后聚类结果进行进一步处理,然后再使用一致性函数。
Summary:
- This paper presents a new link-based approach to improve the conventional matrix.
- Three new link-based algorithms are proposed for the underlying similarity assessment.
- The final clustering result is generated from the refined matrix using two different consensus functions of feature-based and graph-based partitioning.
conventional matrix 就是前言中提到的汇总结果。
这个算法目的是发现一个样本在一个聚类结果中与不属于的类 之间的关系(similarity)。
提炼后的矩阵称为RA matrix ,在这个矩阵上进行一致性曹组有两种方法,基于feature 和基于图切。
对汇总矩阵的提炼的方法一共有三种。
It aims to refine the ensemble-information matrix using the similarity between clusters in the ensemble under examination.
◦Weighted Connected-Triple (WCT)
◦Weighted Triple-Quality (WTQ)
◦Combined Similarity Measure (CSM)
一致性函数有两种:
two new consensus methods are proposed to derive the ultimate clustering result:
◦ feature-based partitioning (FBP)
◦ bipartite graph partitioning (BGP)
下面是一些属性讲解,其实看图比较清楚,一共有N 个样本点,聚类集成框架中使用了M 个聚类方法,得到的结果为π,每个聚类结果π的类个数不一样,使用C 表示:
X ={x1 . . . xN} be a set of N data points
Π={Π 1 . . . ΠM} be a cluster ensemble with M base clusterings
a 图是样本的两个聚类情况,π
1 π
2 ,那么可以有3中结果汇众的表达b-d,后面用得上的是d 图,d图这个矩阵就是作者认为的粗糙聚类结果。
N = 5 样本总数
M = 2 集成框架中的聚类方法个数
K1 = 3,K2 = 2 每个聚类方法中的聚类个数
一个聚类集成问题:
The problem is to find a new partition π* of a data set X that summarizes the information from the cluster ensemble π
final.
This metalevel method involves two major tasks of:
◦1) generating a cluster ensemble
◦2) producing the final partition (normally referred to as a “consensus function”).
为了获取不同的聚类结果,大致归纳如下的聚类模型:
Cluster models:
◦Homogeneous ensembles
◦Different-k
One of the most successful technique is randomly selecting the number of clusters (k) for each ensemble member
◦Data subspace/subsample
◦Heterogeneous ensembles
◦Mixed heuristics
In addition to using one of the aforementioned methods, any combination of them can be applied
而一致性函数归纳如下:
}consensus methods :
◦Feature-based approach
It transforms the problem of cluster ensembles to the clustering of categorical data.
◦Direct approach
◦Pairwise similarity approach
◦Graph-based approach
论文的创新点就是在这两部中间加入了一步提炼:
NOVEL LINK-BASED APPROACH:
◦1) generating a cluster ensemble
◦2)creating the refined ensemble-information matrix using a link-based similarity algorithm
◦3) producing the final partition (normally referred to as a “consensus function”).
计算RA 矩阵公式,在粗糙矩阵下我们可以先知道如下结果,RA 其实就是将d 图中的0,改为 xi 与 C 的相似度,这就是提炼的意思,方法是通关过计算xi属于的类与目标C 的相似度,然后用这个值作为xi 与目标C 的相似度,这就代替了0.
这个算法计算前需要先计算π
1 与 π
2 中类之间的相似度,是两个π之间,π内之间的类相似度怎么算就是这个算法解决的问题。
图示:
C11 类有样本: x1 x2 C21 类有样本: x1 x3
<C11,C21> = {x1}/{x1 x2 x3} = 1/3
在上面的基础上,开始讲解这个算法,算法有3中计算一个聚类中 类间的similary:
Weighted Connected-Triple (WCT):
◦WCT extends the Connected-Triple method.
◦Formally, a triple, Triple =(V
triple ,E
triple), is a subgraph of G’ containing three vertices V
Triple ={v
x,v
y,v
z} ∈V and two edges ETriple ={e
xz,e
yz} ∈E, with e
xz ∉ E.
◦DC ∈[0,1]is a constant decay factor
第一条就是 计算xy点关于z 点得到他们之间的similary,xy 是属于一个聚类类结果的类标号,z 是其他聚类结果的类标号。
第二条就是第一条结果的叠加。
第三条就是正规化后加上约束因子,因为RA-matrix 直接知道的结果为1,计算similarity 的应该小一点。
图示,这就把RA 矩阵补全了,例如x3 与C11 的项取值,就是Xz 属于的类(C12)与 C11 之间的similarity,即0.9
}Weighted Triple-Quality (WTQ)
◦WTQ is inspired by the initial measure of which evaluates the association between personal home pages.
◦Note that the method gives high weights to rare features and low weights to features that are common to most of the pages.
N
z ∈V denotes the set of vertices that is directly linked to the vertex v
z such that ∨v
t ∈N
z; |w
zt| > 0.
第一条就是 xy 关于 z 的权重,该式分母其实就是与z 有相关的w 之和。
其他跟上面的一样的。
Combined Similarity Measure (CSM):
With the objective of obtaining a robust similarity evaluation, this particular algorithm combines the WCT and WTQ measures previously described.
将上面两种方法结合成第三种。
一致性方法的选择:
Consensus Methods for the RA Matrix:
◦Feature-Based Partitioning
k-means (KM)
k-medoids (PAM)
◦Bipartite Graph Partitioning
weight SPEC graph-partitioning
实验结果就不说了,有兴趣的可以下论文能看。
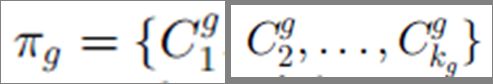
![[论文]A Link-Based Approach to the Cluster Ensemble Problem_第1张图片](http://img.e-com-net.com/image/product/f8e76e7add304de08c78080c4e8c764c.jpg)
![[论文]A Link-Based Approach to the Cluster Ensemble Problem_第2张图片](http://img.e-com-net.com/image/product/04496dfb6b7b4109bd41ec48c84dccbb.jpg)
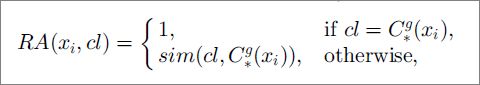
![[论文]A Link-Based Approach to the Cluster Ensemble Problem_第3张图片](http://img.e-com-net.com/image/product/550bceead28840b587fc4b89818ffefc.jpg)
![[论文]A Link-Based Approach to the Cluster Ensemble Problem_第4张图片](http://img.e-com-net.com/image/product/d7b8a4d7f6d342d38ce5429c5ebcc1b8.png)
![[论文]A Link-Based Approach to the Cluster Ensemble Problem_第5张图片](http://img.e-com-net.com/image/product/7309947b283d4964bc711763f09d918d.jpg)
![[论文]A Link-Based Approach to the Cluster Ensemble Problem_第6张图片](http://img.e-com-net.com/image/product/1c9c068c9d9245818bcf73b0b8f44d61.jpg)
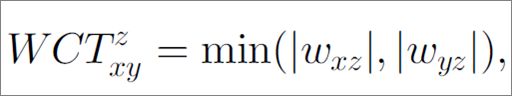
![[论文]A Link-Based Approach to the Cluster Ensemble Problem_第7张图片](http://img.e-com-net.com/image/product/1c01052d271f403089623f99236a2d5d.jpg)
![[论文]A Link-Based Approach to the Cluster Ensemble Problem_第8张图片](http://img.e-com-net.com/image/product/fcba4b6196044a449ff2ca43ba702888.jpg)
![[论文]A Link-Based Approach to the Cluster Ensemble Problem_第9张图片](http://img.e-com-net.com/image/product/7b2f4c2fd3f243f79df10c61fdb17a73.jpg)
![[论文]A Link-Based Approach to the Cluster Ensemble Problem_第10张图片](http://img.e-com-net.com/image/product/940c349f1ce64123b4eaafd7c107669e.jpg)
![[论文]A Link-Based Approach to the Cluster Ensemble Problem_第11张图片](http://img.e-com-net.com/image/product/9a09f794bc85405a8f903cb42e0df4ed.jpg)
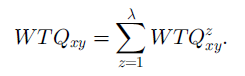
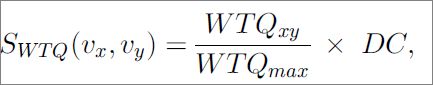
![[论文]A Link-Based Approach to the Cluster Ensemble Problem_第12张图片](http://img.e-com-net.com/image/product/9df18c3cfdb04369b69d267e4f83229b.jpg)
![[论文]A Link-Based Approach to the Cluster Ensemble Problem_第13张图片](http://img.e-com-net.com/image/product/12ba8e4843804ee3892cf957822b6ccf.jpg)
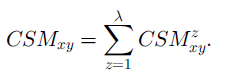
![[论文]A Link-Based Approach to the Cluster Ensemble Problem_第14张图片](http://img.e-com-net.com/image/product/506f7d8971fb468ab4f92de5c75e3c1c.jpg)
![[论文]A Link-Based Approach to the Cluster Ensemble Problem_第15张图片](http://img.e-com-net.com/image/product/3a76a14c5db8432680888d0a77523e5b.jpg)