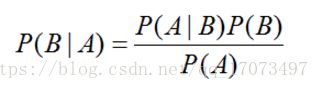朴素贝叶斯分类器 详细解析
1 贝叶斯决策论
贝叶斯决策论(Bayesian decision theory)是概率框架下实施决策的基本方法。对分类任务来说,在所有相关概率都已知的理想情况下,贝叶斯决策轮考虑如何基于这些概率和误判损失来选择最优的类别标记。
1.1 后验概率
P{H0|x}是给定观测值x条件下H0出现的概率,统称为后验概率
For example:
假设一个学校里有60%男生和40%女生。女生穿裤子的人数和穿裙子的人数相等,所有男生穿裤子。一个人在远处随机看到了一个穿裤子的学生。那么这个学生是女生的概率是多少?
使用 贝叶斯定理,事件A是看到女生,事件B是看到一个穿裤子的学生。我们所要计算的是P(A|B)。
P(A)是忽略其它因素,看到女生的概率,在这里是40%
P(A’)是忽略其它因素,看到不是女生(即看到男生)的概率,在这里是60%
P(B|A)是女生穿裤子的概率,在这里是50%
P(B|A’)是男生穿裤子的概率,在这里是100%
P(B)是忽略其它因素,学生穿裤子的概率,P( ) = P( | )P( ) + P( | ')P( '),在这里是0.5×0.4 + 1×0.6 = 0.8.
根据贝叶斯定理,我们计算出后验概率P(A|B)
P(A|B)=P(B|A)*P(A)/P(B)=0.25
可见,后验概率实际上就是条件概率。
1.2 贝叶斯定理
要了解贝叶斯分类,必须了解贝叶斯定理,贝叶斯定理离不开条件概率
条件概率定义:
事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在B条件下A发生的概率”。
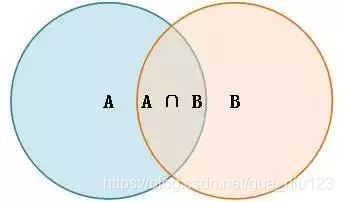
根据文氏图,可以很清楚地看到在事件B发生的情况下,事件A发生的概率就是P(A∩B)除以P(B)。
所以现在只需求得P(A∩B)的概率,![]()
,考虑A∩B概率从B发生的前提下,考虑A∩B概率。
2. 朴素贝叶斯分类算法详解
(1)x=(x1,x2,…xD)表示含有D维属性的数据对象。训练集S含有K个类别,表示为y=(y1,y2,…yK)。
(2)已知待分类数据对象xx,预测xx所属类别,计算方式如下:
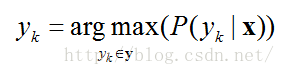
所得yk即为x所属类别。上式表示,已知待分类数据对象xx的情况下,分别计算x属于y1、y2、…、yK的概率,选取其中概率的最大值,此时所对应的yk,即为x所属类别。
(3)根据贝叶斯定理,P(yk|x)计算方式如下:

计算过程中,P(x)对于P(yk|x),相当于常数。因此,若想得到P(yk|x)最大值,只需计算P(x|yk)P(yk)最大值。如果类别的先验概率未知,即P(yk)未知,则通常假定这些类别是等概率的,即P(y1)=P(y2)=…=P(yK)。
(4)假设数据对象xx的各属性之间相互独立,P(x|yk)计算方式如下:
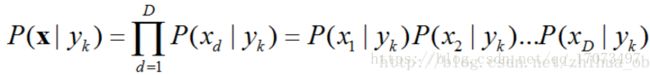
(5)P(xd|yk)的计算方式如下:
如果属性Ad是离散属性或分类属性。训练集中属于类别ykyk的数据对象,在属性AdAd下的相异属性值共有n个;训练集中属于类别yk,且在属性Ad下的属性值为xdxd的数据对象共有m个。因此,P(xd|yk)计算方式如下:

如果属性AdAd是连续属性。通常假设连续属性均服从均值为μμ、标准差为σσ的高斯分布, 即

因此,P(xd|yk)P(xd|yk)计算方式如下:

其中,μykμyk、σykσyk表示训练集中属于类别ykyk的数据对象在属性AdAd下的均值和标准差。
3.例题分析
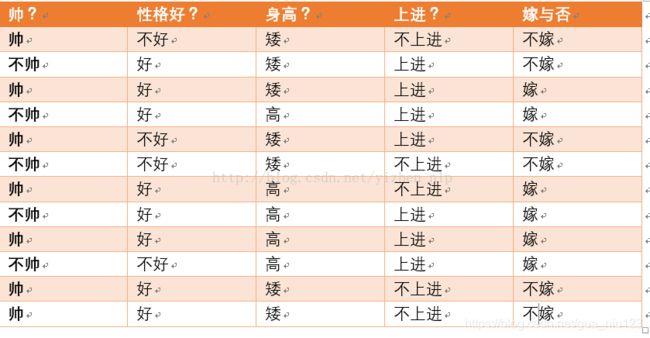
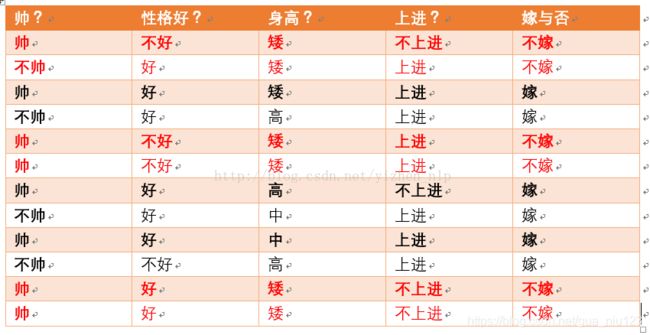
现在给我们的问题是,如果一对男女朋友,男生想女生求婚,男生的四个特点分别是不帅,性格不好,身高矮,不上进,请你判断一下女生是嫁还是不嫁?
这是一个典型的分类问题,转为数学问题就是比较p(嫁|(不帅、性格不好、身高矮、不上进))与p(不嫁|(不帅、性格不好、身高矮、不上进))的概率,谁的概率大,我就能给出嫁或者不嫁的答案!
这里我们联系到朴素贝叶斯公式:
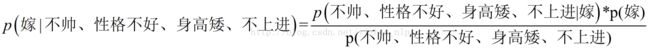
我们需要求p(嫁|(不帅、性格不好、身高矮、不上进),这是我们不知道的,但是通过朴素贝叶斯公式可以转化为好求的三个量.
p(不帅、性格不好、身高矮、不上进|嫁)、p(不帅、性格不好、身高矮、不上进)、p(嫁)(至于为什么能求,后面会讲,那么就太好了,将待求的量转化为其它可求的值,这就相当于解决了我们的问题!)
4 朴素贝叶斯算法的朴素一词解释
那么这三个量是如何求得?
是根据已知训练数据统计得来,下面详细给出该例子的求解过程。
回忆一下我们要求的公式如下:
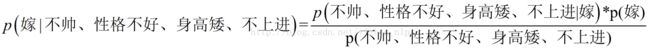
那么我只要求得p(不帅、性格不好、身高矮、不上进|嫁)、p(不帅、性格不好、身高矮、不上进)、p(嫁)即可,好的,下面我分别求出这几个概率,最后一比,就得到最终结果。
p(不帅、性格不好、身高矮、不上进|嫁) = p(不帅|嫁)*p(性格不好|嫁)*p(身高矮|嫁)*p(不上进|嫁),那么我就要分别统计后面几个概率,也就得到了左边的概率!
等等,为什么这个成立呢?学过概率论的同学可能有感觉了,这个等式成立的条件需要特征之间相互独立吧!
对的!这也就是为什么朴素贝叶斯分类有朴素一词的来源,朴素贝叶斯算法是假设各个特征之间相互独立,那么这个等式就成立了!
但是为什么需要假设特征之间相互独立呢?
1、我们这么想,假如没有这个假设,那么我们对右边这些概率的估计其实是不可做的,这么说,我们这个例子有4个特征,其中帅包括{帅,不帅},性格包括{不好,好,爆好},身高包括{高,矮,中},上进包括{不上进,上进},那么四个特征的联合概率分布总共是4维空间,总个数为233*2=36个。
36个,计算机扫描统计还可以,但是现实生活中,往往有非常多的特征,每一个特征的取值也是非常之多,那么通过统计来估计后面概率的值,变得几乎不可做,这也是为什么需要假设特征之间独立的原因。
2、假如我们没有假设特征之间相互独立,那么我们统计的时候,就需要在整个特征空间中去找,比如统计p(不帅、性格不好、身高矮、不上进|嫁),
我们就需要在嫁的条件下,去找四种特征全满足分别是不帅,性格不好,身高矮,不上进的人的个数,这样的话,由于数据的稀疏性,很容易统计到0的情况。 这样是不合适的。
根据上面俩个原因,朴素贝叶斯法对条件概率分布做了条件独立性的假设,由于这是一个较强的假设,朴素贝叶斯也由此得名!这一假设使得朴素贝叶斯法变得简单,但有时会牺牲一定的分类准确率。
好的,上面我解释了为什么可以拆成分开连乘形式。那么下面我们就开始求解!
我们将上面公式整理一下如下:

下面我将一个一个的进行统计计算(在数据量很大的时候,根据中心极限定理,频率是等于概率的,这里只是一个例子,所以我就进行统计即可)。
p(嫁)=?
首先我们整理训练数据中,嫁的样本数如下:

则 p(嫁) = 6/12(总样本数) = 1/2
p(不帅|嫁)=?统计满足样本数如下:

则p(不帅|嫁) = 3/6 = 1/2 在嫁的条件下,看不帅有多少
p(性格不好|嫁)= ?统计满足样本数如下:

则p(性格不好|嫁)= 1/6
p(矮|嫁) = ?统计满足样本数如下:
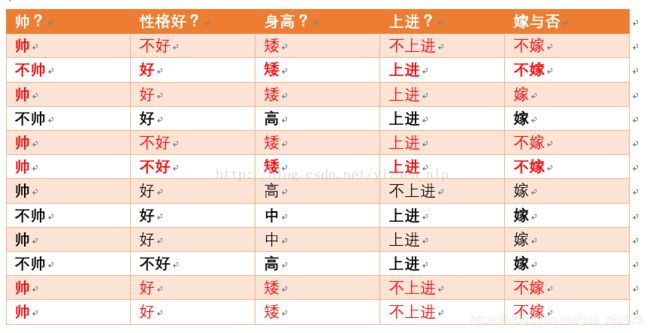
则p(矮|嫁) = 1/6
p(不上进|嫁) = ?统计满足样本数如下:

则p(不上进|嫁) = 1/6
下面开始求分母,p(不帅),p(性格不好),p(矮),p(不上进)
统计样本如下: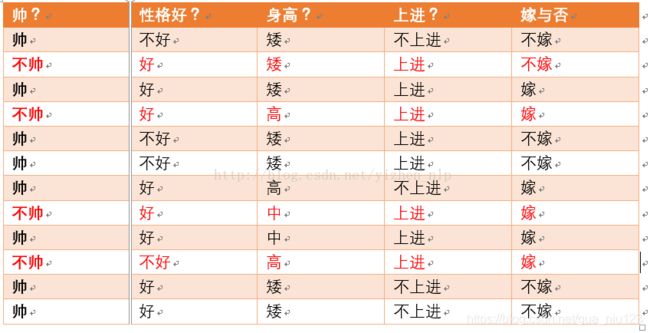
帅统计如上红色所示,占4个,那么p(不帅) = 4/12 = 1/3
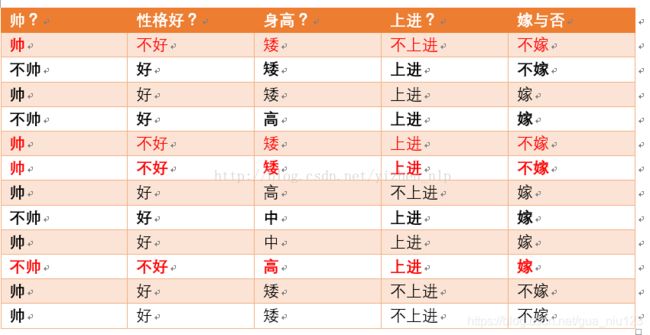
性格不好统计如上红色所示,占4个,那么p(性格不好) = 4/12 = 1/3

身高矮统计如上红色所示,占7个,那么p(身高矮) = 7/12
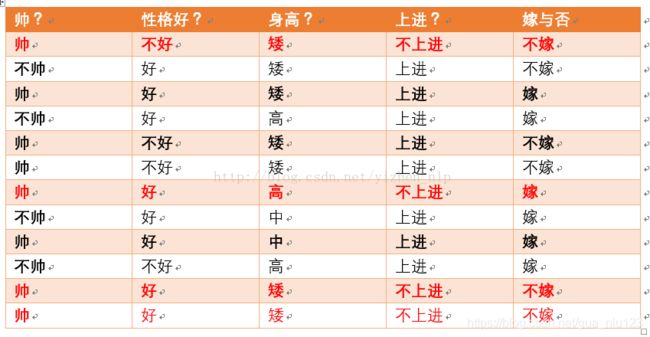
不上进统计如上红色所示,占4个,那么p(不上进) = 4/12 = 1/3
到这里,要求p(不帅、性格不好、身高矮、不上进|嫁)的所需项全部求出来了,下面我带入进去即可,
= (1/21/61/61/61/2)/(1/31/37/12*1/3)
下面我们根据同样的方法来求p(不嫁|不帅,性格不好,身高矮,不上进),完全一样的做法,为了方便理解,我这里也走一遍帮助理解。首先公式如下:

下面我也一个一个来进行统计计算,这里与上面公式中,分母是一样的,于是我们分母不需要重新统计计算!
p(不嫁)=?根据统计计算如下(红色为满足条件):
p(不帅|不嫁) = ?统计满足条件的样本如下(红色为满足条件):
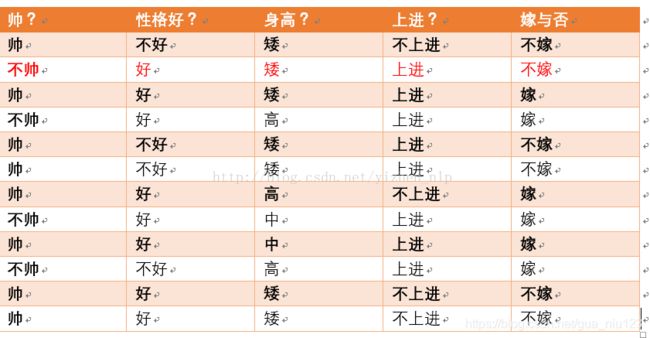
则p(不帅|不嫁) = 1/6
p(性格不好|不嫁) = ?据统计计算如下(红色为满足条件):
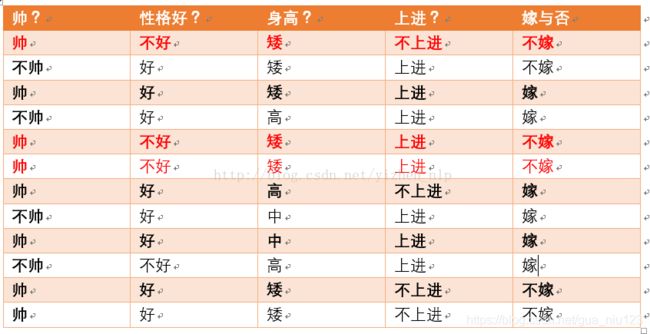
则p(性格不好|不嫁) =3/6 = 1/2
p(矮|不嫁) = ?据统计计算如下(红色为满足条件):

则p(矮|不嫁) = 6/6 = 1
p(不上进|不嫁) = ?据统计计算如下(红色为满足条件):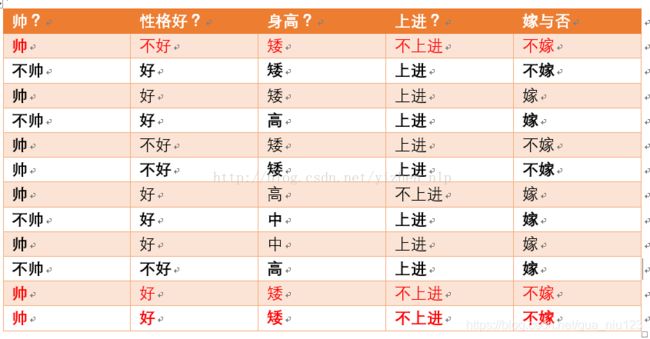
则p(不上进|不嫁) = 3/6 = 1/2
那么根据公式:
p (不嫁|不帅、性格不好、身高矮、不上进) = ((1/61/211/2)1/2)/(1/31/37/12*1/3)
很显然(1/61/211/2) > (1/21/61/61/6*1/2)
于是有p (不嫁|不帅、性格不好、身高矮、不上进)>p (嫁|不帅、性格不好、身高矮、不上进)
所以我们根据朴素贝叶斯算法可以给这个女生答案,是不嫁!!!!
4. 朴素贝叶斯分类的优缺点
优点:
(1) 算法逻辑简单,易于实现(算法思路很简单,只要使用贝叶斯公式转化一下即可!)
(2)分类过程中时空开销小(假设特征相互独立,只会涉及到二维存储)
缺点:
理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。
而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。