【GANs】Generative Adversarial Nets
【GANs】Generative Adversarial Nets
- 1 GAN
-
- 1.1 GANs的简介
- 1.2 思想与目标函数
- 1.3 GAN代码
- 1.4 全局最优推导
- 1.5 GANs方向展望
1 GAN
笔记视频链接
1.1 GANs的简介
Generative Adversarial Nets原文链接
-
判别器模型(网络):一般熟知的带标签的分类、回归等监督学习都属于判别器模型。学习的是某种分布下的条件概率分布 p ( y ∣ x ) p(y|x) p(y∣x)。
-
生成器模型(网络):聚类、自动编码器等无监督学习模型。学习的是联合分布概率 p ( x , y ) p(x,y) p(x,y)。通过模型学习到最优的 p ( x ∣ y ) p(x|y) p(x∣y)
在现实中,判别模型在分类工作中的表现通常优于生成模型,但在一些创造性的工作中显然生成模型更有意义。
1.2 思想与目标函数
生成器和判别器不断对抗博弈,直到两个网络到达最终的动态均衡状态,即判别器无法识别生成器的图像真假。

我们想学习到的是像训练集那样的数据分布: p g ( z ) p_g(z) pg(z)➡真实数据分布, z z z是噪声。
但是 我们可知道的是,极大似然函数去找概率分布会有很复杂的计算问题,因此我们才看作者采用的方式,绕过极大似然函数来逼近真实数据分布。
逼近过程:
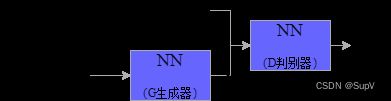
x ∼ P d a t a x \sim P_{data} x∼Pdata
z ∼ P z z \sim P_z z∼Pz
- 我们看训练 D D D(想让 D D D性能高):
if x is from Pdata : D(x) ↑ --→ log(D(x)) ↑
if z is from Pz : D(G(z)) ↓ --→ 1 - D(G(z)) ↑ <=> log(1 - D(G(z))) ↑
得到关于 D D D的目标函数
D m a x E x ∼ P d a t a [ l o g D ( x ) ] + E z ∼ P z ( 1 − D ( G ( z ) ) ) ^{max}_{\space\space\space D} E_{x \sim P_{data}}[logD(x)] + E_{z \sim P_z}(1-D(G(z))) DmaxEx∼Pdata[logD(x)]+Ez∼Pz(1−D(G(z)))
- 在来看训练 G G G(想让 G G G性能高):
z is from Pz : D(z) ↑ --→ 1-D(G(z)) ↓ <=> log(1-D(G(z))) ↓
得到关于 G G G的目标函数:
G m i n E z ∼ P z ( 1 − D ( G ( z ) ) ) ^{min}_{\space\space\space G} E_{z \sim P_z}(1-D(G(z))) GminEz∼Pz(1−D(G(z)))
由 G G G和 D D D的两个目标,得到总的目标函数:(GAN原始论文中的目标函数)
G m i n D m a x E x ∼ P d a t a [ l o g D ( x ) ] + E z ∼ P z ( 1 − D ( G ( z ) ) ) {^{min}_{\space\space\space G}} {^{max}_{\space\space\space D}} E_{x \sim P_{data}}[logD(x)] + E_{z \sim P_z}(1-D(G(z))) Gmin DmaxEx∼Pdata[logD(x)]+Ez∼Pz(1−D(G(z)))
以这个目标函数训练下去, G G G和 D D D将在博弈中达到最优。
全局最优存在且函数收敛,在介绍完代码后证明。
1.3 GAN代码
# GAN_2014.py
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras import Sequential,Model
from tensorflow.keras.layers import Dense,Reshape,Input,Flatten
from tensorflow.keras.layers import LeakyReLU,BatchNormalization
from tensorflow.keras.datasets import mnist
from tensorflow.keras.optimizers import Adam
class GAN():
def __init__(self):
self.latent_dim = 100
self.img_rows = 28
self.img_cols = 28
self.channel = 1
self.img_shape = (self.img_rows,self.img_cols,self.channel)
self.discrinator = self.build_discrinator() # 构建
optimizer = Adam(0.0002,0.5)
self.discrinator.compile(loss='binary_crossentropy',
optimizer=optimizer,
metrics=['accuracy'])
self.generator = self.build_generator() # generator就可以完成从noise到img的生成
self.discrinator.trainable = False
z = Input(shape=(self.latent_dim,))
img = self.generator(z)
validity = self.discrinator(img)
self.combined = Model(z,validity)
self.combined .compile(loss='binary_crossentropy',optimizer=optimizer) # 完成了叠加模型的构建
# 构建生成器模型
def build_generator(self):
model = Sequential()
# 添加一层全连接层
model.add(Dense(256, input_dim=self.latent_dim )) # 输入噪声是一维含有100个元素的向量
model.add(LeakyReLU(alpha=0.2))
model.add(BatchNormalization(momentum=0.8)) # BN层
model.add(Dense(512))
model.add(LeakyReLU(alpha=0.2))
model.add(BatchNormalization(momentum=0.8)) # BN层
model.add(Dense(1024))
model.add(LeakyReLU(alpha=0.2))
model.add(BatchNormalization(momentum=0.8)) # BN层
model.add(Dense(np.prod(self.img_shape),activation='tanh')) # 神经元个数(输出)等于图像尺寸乘积
model.add(Reshape(self.img_shape)) # reshape成图像形状 28*28*1
model.summary() # 记录各层参数情况
noise = Input(shape=(self.latent_dim,))
img = model(noise)
return Model(noise,img) # 返回输入为噪声,输出为预测图的Model
# 构建判别器模型
def build_discrinator(self):
# 需要输入图片 然后判别真假 img--→label
model = Sequential()
model.add(Flatten(input_shape=self.img_shape)) # 将图像拉成一维
model.add(Dense(512))
model.add(LeakyReLU(alpha=0.2))
model.add(Dense(256))
model.add(LeakyReLU(alpha=0.2))
model.add(Dense(1,activation='sigmoid')) # 输出结果落在0-1概率区间
model.summary() # 记录各层参数情况
img = Input(shape=self.img_shape)
validity = model(img) # 将输入图输入模型之后预测出来的输出概率
return Model(img,validity) # 由图像生成可能性
def train(self,epochs,batch_size=128,sample_interval=50):
# 获取mnist手写数字数据集
(X_train, _),(_,_) = mnist.load_data() # shape : 60000*28*28
# 将图像值转化成(-1,1)
X_train = X_train / 127.5 - 1.
X_train = np.expand_dims(X_train,axis=3) # 扩展成60000*28*28*1
valid = np.ones((batch_size, 1)) # 完成对Batch个图像进行1标签的操作
fake = np.zeros((batch_size,1)) # 完成对虚假图像进行0标签的操作
for epoch in range(epochs):
# ---------------------------
# 训练判别器
# ---------------------------
# 选择batch_size个图像样本(随机)
idx = np.random.randint(0,X_train.shape[0],batch_size)
imgs = X_train[idx] # batch_size*28*28*1 真实样本
noise = np.random.normal(0,1,(batch_size,self.latent_dim))
# 使用生成器将noise生成img
gen_imgs = self.generator.predict(noise) # 完成了噪声生成图像 也就是 虚假图像
d_loss_real = self.discrinator.train_on_batch(imgs,valid)
d_loss_fake = self.discrinator.train_on_batch(gen_imgs,fake)
d_loss = 0.5 * np.add(d_loss_fake, d_loss_real)
# 完成了对判别器的训练
# ---------------------------
# 训练生成器
# ---------------------------
noise = np.random.normal(0,1,(batch_size,self.latent_dim)) # batch_size*100
g_loss = self.combined.train_on_batch(noise,valid)
print('%d [D loss: %f, acc.: %.2f%%] [G loss: %f]' % (epoch,d_loss[0], 100*d_loss[1],g_loss))
# 每200轮保存一个Batch图像
if epoch % sample_interval == 0:
self.sample_images(epoch)
def sample_images(self,epoch):
r,c = 5,5
noise = np.random.normal(0,1,(r*c,self.latent_dim))
gen_imgs = self.generator.predict(noise)
# Rescale image 0 - 1
gen_imgs = 0.5 * gen_imgs + 0.5
fig,axs = plt.subplots(r,c)
cnt = 0
for i in range(r):
for j in range(c):
axs[i,j].imshow(gen_imgs[cnt, :, :, 0],cmap='gray')
axs[i,j].axis('off')
cnt += 1
fig.savefig('images/%d.png' % epoch)
plt.close()
if __name__ == '__main__':
gan = GAN()
gan.train(epochs=30000,batch_size=32,sample_interval=200)
tree
test
│ GAN_2014.py
└─ images
1.4 全局最优推导

x ∼ P d a t a x \sim P_{data} x∼Pdata
z ∼ P z z \sim P_z z∼Pz
总目标函数: G m i n D m a x E x ∼ P d a t a [ l o g D ( x ) ] + E z ∼ P z ( 1 − D ( G ( z ) ) ) {^{min}_{\space\space\space G}} {^{max}_{\space\space\space D}} E_{x \sim P_{data}}[logD(x)] + E_{z \sim P_z}(1-D(G(z))) Gmin DmaxEx∼Pdata[logD(x)]+Ez∼Pz(1−D(G(z)))
- 常规生成模型:是要对生成器进行建模,也就是求出生成图片的概率分布 P g P_g Pg,其参数为 θ g \theta_g θg,然后通过极大似然法: arg min K L ( P d a t a ∣ ∣ P g ) \arg \min KL(P_{data} || P_g) argminKL(Pdata∣∣Pg)
其中 K L KL KL散度表示 P d a t a P_{data} Pdata(目标概率分布) 与 P g P_g Pg(近似 P P P的概率分布)的信息损失量化。
而GAN利用对抗学习逼近 P d a t a P_{data} Pdata
记 V ( D , G ) = G m i n D m a x E x ∼ P d a t a [ l o g D ( x ) ] + E x ∼ P g ( 1 − D ( x ) ) V(D,G) = {^{min}_{\space\space\space G}} {^{max}_{\space\space\space D}} E_{x \sim P_{data}}[logD(x)] + E_{x \sim P_g}(1-D(x)) V(D,G)= Gmin DmaxEx∼Pdata[logD(x)]+Ex∼Pg(1−D(x)),其中 x = G ( z ) x=G(z) x=G(z),那么 G ( z ) G(z) G(z)就变成了来自 G G G的概率分布数据(含有生成器参数)
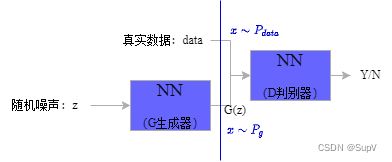
先固定 G G G,求 V V V的最大值 ( D m a x V ( D , G ) ) (^{max}_{\space\space\space D}V(D,G)) ( DmaxV(D,G))
推导过程:
D m a x V ( D , G ) = ∫ P d a t a [ log ( D ( x ) ) ] d x + ∫ P g [ log ( 1 − D ( x ) ) ] d x = ∫ P d a t a [ log ( D ) ] d x + ∫ P g [ log ( 1 − D ) d x \begin{align} {^{max}_{\space\space\space D}V(D,G)} &=\int {{P_{data}}[\log (D(x))]dx + } \int {{P_g}[\log (1 - D(x))]dx} \\ &=\int {{P_{data}}[\log (D)]dx + } \int {{P_g}[\log (1 - D)dx} \end{align} DmaxV(D,G)=∫Pdata[log(D(x))]dx+∫Pg[log(1−D(x))]dx=∫Pdata[log(D)]dx+∫Pg[log(1−D)dx
∂ max D V ( D , G ) ∂ D = ∫ ∂ P d a t a [ log ( D ) + P g log ( 1 − D ) ] ∂ D d x = ∫ P d a t a 1 D + P g − 1 1 − D d x = 0 \frac{{\partial \mathop {\max }\limits_D V(D,G)}}{{\partial D}} = \int {\frac{{\partial {P_{data}}[\log (D) + {P_g}\log (1 - D)]}}{{\partial D}}dx = \int {{P_{data}}\frac{1}{D} + {P_g}\frac{{ - 1}}{{1 - D}}dx = 0} } ∂D∂DmaxV(D,G)=∫∂D∂Pdata[log(D)+Pglog(1−D)]dx=∫PdataD1+Pg1−D−1dx=0
偏导等于 0 0 0时,取得最大值,此时 P d a t a 1 D + P g − 1 1 − D d x = 0 {{P_{data}}\frac{1}{D} + {P_g}\frac{{ - 1}}{{1 - D}}dx = 0} PdataD1+Pg1−D−1dx=0
那么求出: D g ∗ = P d a t a P d a t a + p g D^*_g=\frac{P_{data}}{P_{data}+p_g} Dg∗=Pdata+pgPdata,也就是当 G G G固定, D g ∗ = P d a t a P d a t a + p g D^*_g=\frac{P_{data}}{P_{data}+p_g} Dg∗=Pdata+pgPdata时, V V V取得最大值。
代入最优值: D g ∗ = P d a t a P d a t a + p g D^*_g=\frac{P_{data}}{P_{data}+p_g} Dg∗=Pdata+pgPdata,求 V V V最小值。(也就是 G m i n V ( D , G ) ^{min}_{\space\space\space G}V(D,G) GminV(D,G))
得:
G m i n V ( D , G ) = D m i n V ( D g ∗ , G ) = G m i n ( E x ∼ P d a t a l o g P d a t a P d a t a + p g + E x ∼ P g P d a t a P d a t a + p g ) ^{min}_{\space\space\space G}V(D,G)=^{min}_{\space\space\space D}V(D^*_g,G)=^{min}_{\space\space\space G}(E_{x \sim P_{data}}log\frac{P_{data}}{P_{data}+p_g}+ E_{x \sim P_g}\frac{P_{data}}{P_{data}+p_g}) GminV(D,G)= DminV(Dg∗,G)= Gmin(Ex∼PdatalogPdata+pgPdata+Ex∼PgPdata+pgPdata)
引入 K L KL KL散度概念: D K L ( p ∣ ∣ q ) = E [ l o g p ( x ) − l o g q ( x ) ] D_{KL}(p||q)=E[logp(x)-logq(x)] DKL(p∣∣q)=E[logp(x)−logq(x)]
其中 p , q p,q p,q需要符合概率分布 ( 0 − 1 ) (0-1) (0−1), P d a t a , P g P_{data},P_g Pdata,Pg都是符合概率分布 ( 0 − 1 ) (0-1) (0−1)的,因此可以将分母转化为 ( P d a t a + P g ) / 2 (P_{data}+P_g)/2 (Pdata+Pg)/2就可以转化为 K L KL KL散度公式。
max D V ( D , G ) = min G ( E x ∼ P d a t a l o g P d a t a ( P d a t a + P g ) / 2 ∗ 1 / 2 + E x ∼ P g l o g P g ( P d a t a + P g ) / 2 ∗ 1 / 2 ) = min G K L ( P d a t a ∣ ∣ P d a t a + P g 2 ) + K L ( P g ∣ ∣ P d a t a + P g 2 ) + l o g ( 1 / 4 ) ≥ − l o g 4 \begin{align} {\max \limits_D} V(D,G)&={\min \limits_G}( E_{x \sim {P_{data}}} log\frac{P_{data}}{(P_{data}+P_g)/2} *1/2+ E_{x \sim {P_{g}}} log\frac{P_{g}}{(P_{data}+P_g)/2}*1/2 )\\ &= {\min \limits_G}KL( {P_{data}} ||\frac{P_{data}+P_g}{2}) + KL( {P_{g}} ||\frac{P_{data}+P_g}{2})+log(1/4) \ge -log4 \end{align} DmaxV(D,G)=Gmin(Ex∼Pdatalog(Pdata+Pg)/2Pdata∗1/2+Ex∼Pglog(Pdata+Pg)/2Pg∗1/2)=GminKL(Pdata∣∣2Pdata+Pg)+KL(Pg∣∣2Pdata+Pg)+log(1/4)≥−log4
当 P d a t a = P d a t a + P g 2 = P g P_{data}=\frac{P_{data}+P_g}{2}=P_g Pdata=2Pdata+Pg=Pg时, ′ = ′ '=' ′=′成立,也就是当 P d a t a = P g P_{data}=P_g Pdata=Pg.
D g ∗ = P d a t a + P g 2 = 1 2 D^*_{g}=\frac{P_{data}+P_g}{2}=\frac{1}{2} Dg∗=2Pdata+Pg=21时,接近稳定点,训练结束达到全局最优解。
1.5 GANs方向展望
GAN相关
-
自提出以来持续火热
CVPR等顶会论文20年超过100篇相关论文,21年110篇,不断改进GAN的生成器判别器网络模型,甚至将最近的SOTA模型中的Transformer与GAN结合作出了研究成果。 -
创作方面
在图像生成,风格转换,学习创造性风格上表现优异。 -
图像修复、画质提升
在图像修复,画质提升,场景还原上也有广泛应用。 -
视频生成,语言融合
在视频生成,语义融合中也有广泛应用。
论文方向
-
Architecture
优化网络结构,优化生成器和判别器的结构,提升整体性能,提出更先进创新的思想或者完成更广泛的应用。 -
Efficiency
GANs训练不稳定,训练较慢,可以从提高训练效率入手进行创新。 -
Application
将已有技术整合,或创新已有技术应用到新的领域,作出新的贡献。 -
Training Strategy
从训练策略入手,添加预训练模型等,优化网络性能。
