生成对抗网络（Generative Adversarial Nets, GANs）

代码实现： 基于Tensorflow2.2实现，代码见gitub。

参考文献
1. Generative Adversarial Nets
2. Understanding Generative Adversarial Networks (GANs)
3. 对抗生成网络学习（一）——GAN实现mnist手写数字生成(tensorflow实现)

---

生成对抗网络（Generative Adversarial Networks，GANs）通过让两个神经网络相互博弈，生成器网络基于给定随机输入生成“假数据”，判别器网络负责识别“真假”数据，最终获得能够生成真实数据的生成器。

生成器主要需解决的问题是，将给定先验随机分布的向量，转换为服从期望分布的向量，因此这面临两个问题：第一个问题，期望分布复杂、高维；第二个问题，若已知样本是否来自于期望分布，我们该如何表达期望分布。

该如何解决上述两个问题呢？使用神经网络作为函数的变换方法，即使用“一个非常复杂的函数”将一个简单的M维随机变量映射为一个N维随机变量。这个复杂变换函数并不能直接通过取CDF（累积分布函数）闭式逆获得，需从真实分布中学习获得。

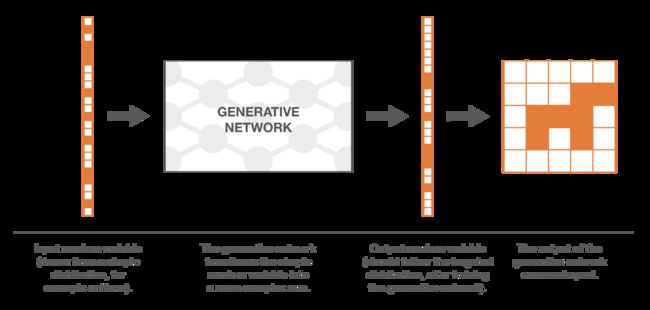
生成神经网络的训练有两种方法：直接方法和间接方法。直接方法就是生成匹配网络GMNs（不是本文重点，参考文献2），间接方法就是生成对抗网络。

GANs

生成对抗网络包含一个生成器$G$（generator）和判别器$D$（discriminator），$G$和$D$均使用多层感知机。

• 定义生成器$G_z(z;{\theta }_g)$，生成器将输入噪声先验分布$p_z(z)$（如均匀分布、高斯分布），尽可能映射为真实数据分布。
• 定义判别器$D(x;{\theta }_d)$，判别器将输出映射为输出标量，表示数据来自于真实分布的概率。

训练判别器，使之尽可能区分输入来自于真实样本还是生成器生成样本；训练生成器，尽可能使判别器对其输出认为是来自于真实样本。因此，生成器和判别器互相对抗，优化判别器降低目标函数值、优化生成器提高目标函数值，目标函数表示为
$$\underset{G}{\min }\underset{D}{\max }V(D,G)={\mathbb{E}}_{x\sim p_{data}}[\log D(x)]+{\mathbb{E}}_{z\sim p_z}[\log (1-D(G(z)))]\text{\hspace{1em}(1)}$$

训练过程中不断优化判别器，在有限训练集下，可易造成overfitting。因此，我们依次执行：迭代$k$步优化判别器（固定生成器），再迭代1步优化生成器（固定判别器），GANs的训练如下算法1所示：

实际训练时，若基于公式(1) 训练生成器，在训练前期，可能无法提供足够大的梯度更新生成器参数，这是因为 判别器在训练前期可以轻易地区分数据是否来自于真实分布，$D(G(z))\to 0$，即$\log (1-D(G(z)))$饱和，因此我们将生成器优化目标函数改为等价形式：
$$\underset{G}{\max }{\mathbb{E}}_{z\sim p_z(z)}[\log D(G(z))]$$

理解为什么$\log (1-D(G(z)))$训练前期饱和？

令$x=D(G(z))$，$y=\log (1-x)$，则
$$\nabla y=1/(x-1),x\to 0^{+}⟹\nabla y\to -1$$

若令$y^{\prime }=\log (x)$，则
$$\nabla y=1/x,x\to 0^{+}⟹\nabla y\to +\infty$$

可见当$x\to 0^{+}$时，$y^{\prime }$比$y$的梯度更大，最大化$\log D(G(z))$能够获得足够大的梯度更新生成器参数！此外，$y^{\prime }$的梯度随着训练进行逐渐减小，这也符合参数更新策略。

GANs理论推导

生成器模型隐式定义了模型生成样本$G(z)$的概率分布$p_g$，其中模型输入$z$服从概率分布$p(z)$（随机噪声），通过训练我们想要尽可能使$p_g$和$p_{data}$同分布，使得生成器可以生成真实数据！

GANs训练过程中，生成器和判别器模型变化如下：

图1中，蓝色虚线表示判别器模型分布，黑点线表示训练样本分布，绿实线表示生成器生成的样本分布，上下水平线分别为$x$和$z$定义域的一部分，向上箭头表示生成器映射$x=G(z)$如何将非均匀分布$p_g$作用在转换后的样本上。

• a. 生成器生成样本分布$p_g$近似于样本真实分布$p_{data}$，判别器有一定的区分力；
• b. 判断器基本收敛；
• c. 判断器梯度引流$G(z)$到更可能分类为真实数据的区域，数次更新后，生成器生成样本分布近似于真实样本分布；
• d. 生成器生成样本分布$p_g$等于样本真实分布$p_{data}$，判别器和生成器接近稳定点，无法继续更新，判别器将无法区分样本来自于真实分布还是生成分布，即随机预测，对应概率均为1/2，sigmoid输出为0，判别模型分布对应水平线；

全局最优解

固定任意生成器$G$，则判别器$D$的最优解为
$$D_G^{\ast }(x)=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}\text{\hspace{1em}(2)}$$

给定任意生成器$G$和判别器$D$，最大化目标函数
$$\begin{array}{rl}V(G,D)& ={\int }_x{p}_{data}(x)\log (D(x))\text{d}x+{\int }_z{p}_z(z)\log (1-D(G(z)))\text{d}z\\ & ={\int }_x{p}_{data}(x)\log (D(x))+p_g(x)\log (1-D(x))\text{d}x\end{array}\text{\hspace{1em}(3)}$$

不理解dz到dx是如何变换的？？？x来自于真实数据集，而z来自于随机噪声分布，上式变换是不是已经假定x和G(z)同分布了！

对于任意$(a,b)\in {\mathbb{R}}^2$，函数$a\log y+b\log (1-y)$在$[0,1]$区间内的最大值为$a/(a+b)$，因此判别器的最优解为公式(2)。

注意到，训练判别器的目标函数可解释为最大化条件概率分布$P(Y|x)$，其中$Y$指示$x$来自于真实分布$p_{data}$，还是来自于生成分布$p_g$。公式(1)最大最小化可被重塑为
$$\begin{array}{rl}C(G)& =\underset{D}{\max }V(G,D)\\ & ={\mathbb{E}}_{x\sim p_{data}}[\log D_G^{\ast }(x)]+{\mathbb{E}}_{z\sim p_z}[\log (1-D_G^{\ast }(G(z)))]\\ & ={\mathbb{E}}_{x\sim p_{data}}[\log D_G^{\ast }(x)]+{\mathbb{E}}_{x\sim p_g}[\log (1-D_G^{\ast }(G(x)))]\\ & ={\mathbb{E}}_{x\sim p_{data}}\left[\log \frac{p_{data}(x)}{p_{data}(x)+p_g(x)}\right]+{\mathbb{E}}_{x\sim p_g}\left[\log \frac{p_g(x)}{p_{data}(x)+p_g(x)}\right]\end{array}\text{\hspace{1em}(4)}$$

定理1. 当前仅当$p_g=p_{data}$时，目标函数$C(G)$获得最小值$-\log 4$，这意味极小化$C(G)$，使得分布$p_g$逼近$p_{data}$.

先证充分性，若$p_g=p_{data}$，则$D_G^{\ast }(x)=1/2$，因此$C(G)=-\log 4$.

再证必要性，根据JS散度证明：
$$\begin{array}{rl}C(G)& =KL(p_{data}||p_{data}+p_g)+KL(p_g||p_{data}+p_g)\\ & =\frac{}{}KL\left(p_{data}\left|\right|\frac{p_{data}+p_g}{2}\right)+\frac{}{}KL\left(p_g\left|\right|\frac{p_{data}+p_g}{2}\right)-2\log 2\\ & =2JSD(p_{data}||p_g)-\log 4\end{array}$$
当前仅当$p_g=p_{data}$时，JS散度取极小值0，必要性得证。从KL角度理解，取两个KL散度取极小值0，当前仅当：
$$p_{data}=\frac{p_{data}+p_g}{2}=p_g⟹p_g=p_{data}$$

训练过程的收敛性

每次训练判别器时，固定生成器，若判别器可获得最优解，则生成器最大化目标函数：
$$V(G,D_G^{\ast })=\max {\mathbb{E}}_{x\sim p_{data}}[\log D_G^{\ast }(x)]+{\mathbb{E}}_{x\sim p_g}[\log (1-D_G^{\ast }(x))]$$

也就是说，若最大化$V(G,D_g^{\ast })$，则$p_g$收敛至$p_{data}$.

证明：
考虑$V(G,D)=U(p_g,D)$，$U$是关于$p_g$的凸函数，则函数$U$存在唯一最优解！如何证明$U$是凸函数，此处省略。

优缺点

GANs缺点： 不能清晰地表达$p_g(x)$，而且生成器和判别器需同步训练，在未有效更新判别器前，生成器不能过度训练（过度训练生成器可能导致生成器将多数输入映射真实数据分布$P_{data}$中的相同样本），保证有足够的数据多样本建模/拟合真实数据分布$p_{data}$，就像波尔曼兹机的负链一样，在不同迭代步见需保持最新。

GANs优点： 不需要马尔科夫链，使用BP算法更新参数，不需要近似推理，使得模型中可以添加各式各样的函数。此外，生成器不直接通过真实数据样本更新其参数，而是通过判别器输出的梯度更新，使得对抗模型具有以下统计优势。