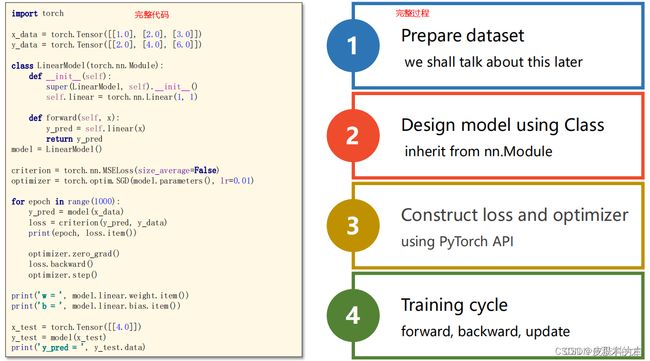
PyTorch 深度学习实践 第5讲
PyTorch 深度学习实践 第5讲
B站 刘二大人 ,传送门用PyTorch实现线性回归
PyTorch Fashion(风格)
1、准备数据集 prepare dataset
- 计算预测值y_pred的模型
2、模型设计 design model using Class # 目的是为了前向传播forward,即计算y hat(预测值)
- 使用pytorch封装好的API即可
3、构造损失函数和优化器 Construct loss and optimizer (using PyTorch API) 其中,计算loss是为了进行反向传播,optimizer是为了更新梯度。
- 前馈——计算损失
- 反馈——计算梯度
- g更新——用梯度下降算法更新权重
4、训练 Training cycle (forward,backward,update)

要确定w,就要知道x和\hat{y}的维度,上图中y:3×1,x:3×1,w就得是3×3的。
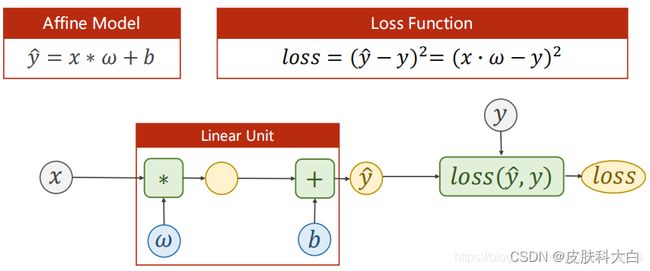
计算图中的Linear Unit就可以直接用torch.nn.Linear(in_feature,out_feature,bias=True)来构造,in_feature是输入维度(维度是矩阵的列),out_feature是输出维度。torch.nn.Linear是pytorch的一个类,此处是在构造对象,包含w和b两个tensor,自动进行w*x+b的计算,linear是继承自Module,能进行反向传播。
第一步——准备数据集 prepare dataset
用mini-batch构造数据集,x和y必须是矩阵的形式
将数据集定义成矩阵形式(张量),如下x_data, y_data都是3X1的矩阵,权重w也被当成矩阵进行参与计算。w也是3X1矩阵,与x_data矩阵进行点乘,对应位置元素相乘(不是矩阵相乘)。

第二步——模型设计
设计模型也就是构造计算图的过程,需要已知x和y的维度,由此可以确定w和b的维度。计算梯度时只需要从loss处反向一步一步求出即可,不需要手动求偏导,有了这个从w和x求出loss的模型之后,用反向传播就可以自动求出这条链上的梯度。

最后计算出的loss是一个标量数值???,才可以调用backward():
loss经过计算最终是一个0维张量,也就是标量,向量没办法backward
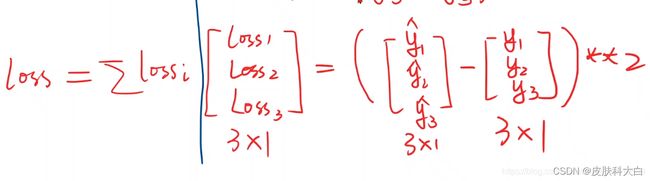
最基本的代码框架
把模型定义成一个类LinearModel,继承自torch.nn.Module。构造计算图,所有的神经网络模型都要继承Module类。
class LinearModel(torch.nn.Module):
# 构造函数——初始化变量
def __init__(self):
super(LinearModel, self).__init__()
# 构造对象 线性模型
self.linear = torch.nn.Linear(1, 1)
# 对module类中原forward函数的重写
def forward(self, x):
# linear——可调用对象 linear(x), __call__函数
y_pred = self.linear(x)
return y_pred
# model也是一个可调用对象
model = LinearModel()
代码说明:
1、Module实现了魔法函数__call__(),call()里面有一条语句是要调用forward()。因此新写的类中需要重写forward()覆盖掉父类中的forward()
2、call函数的另一个作用是可以直接在对象后面加(),例如实例化的model对象,和实例化的linear对象
3、本算法的forward体现是通过以下语句实现的:
y_pred = model(x_data)
由于魔法函数call的实现,model(x_data)将会调用model.forward(x_data)函数,model.forward(x_data)函数中的
关于魔法函数call在PyTorch中的应用的进一步解释:
pytorch 之 call, init,forward
pytorch系列nn.Modlue中call的进一步解释
y_pred = self.linear(x)
注意一个细节:y_pred = self.linear(x),在对象后面加括号实现一个可调用对象。
在Module类的__call__()就是调用forward()。
self.linear(x)也由于魔法函数call的实现将会调用torch.nn.Linear类中的forward,至此完成封装,也就是说forward最终是在torch.nn.Linear类中实现的,具体怎么实现,可以不用关心,大概就是y= wx + b。

self.linear = torch.nn.Linear(1, 1)
# Linear类的格式如下图所示,in_features是输入数据的维数,y_features是输出样本的维数,bias是偏置值,默认是True
# 实例化对象之后相当于进行y = xw + b的计算

上述self.linear = torch.nn.Linear(1, 1)的(1,1)就是对于参数in_features和out_features:linearmodule会自动backward,nn.Linear是一类 包含weight 和bias两个Tensor
关于w的维度问题,如图所示的两种形式
第三步——构造损失函数和优化器
# MSELoss类继承自Module,torch.nn.MSELoss,可调用,pytorch提供的MSE损失函数。
criterion = torch.nn.MSELoss(size_average=False)
# 实例化一个优化器对象
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

torch.nn.MSELoss 类如图所示,size_average表示损失是否求均值;reduce表示求出的损失是否降维,默认为True,在这个例子中就是将loss转换为标量。
torch.nn.MSELoss类也继承于nn.Module类,参数有size_average=True(是否求均值,当N大小一样时,如果大家都不求,效果是一样的)和reduce=True(最终是否要进行降维,就是是否要求和)。
torch.nn.MSELoss也跟torch.nn.Module有关,参与计算图的构建,torch.optim.SGD与torch.nn.Module无关,不参与构建计算图。
优化器:
torch.optim
torch.optim是一个实现了各种优化算法的库,Pytoch中用来优化模型权重的类是torch.optim.Optimizer, 我们常见的优化器都是Optimizer这个基类的子类;
如何使用optimizer
为了使用torch.optim,你需要构建一个optimizer对象。这个对象能够保持当前参数状态并基于计算得到的梯度进行参数更新。
构建
为了构建一个Optimizer,你需要给它一个包含了需要优化的参数(必须都是Variable对象)的iterable。然后,你可以设置optimizer的参数选项,比如学习率,权重衰减,等等。
- 为所有参数设置相同参数选项
例子:
optimizer = optim.SGD(model.parameters(), lr = 0.01, momentum=0.9)
optimizer = optim.Adam([var1, var2], lr = 0.0001)
optim.SGD([
{'params': model.base.parameters()},
{'params': model.classifier.parameters(), 'lr': 1e-3}
], lr=1e-2, momentum=0.9)
这意味着model.base的参数将会使用1e-2的学习率,model.classifier的参数将会使用1e-3的学习率,并且0.9的momentum将会被用于所有的参数。
进行单次优化
所有的optimizer都实现了step()方法,这个方法会更新所有的参数。
能按如下两种方式来使用:
- optimizer.step()
这是大多数optimizer所支持的简化版本。一旦梯度被如backward()之类的函数计算好后,我们就可以调用这个函数。
例子
for input, target in dataset:
optimizer.zero_grad()
output = model(input)
loss = loss_fn(output, target)
loss.backward()
optimizer.step()
2. optimizer.step(closure)
一些优化算法例如Conjugate Gradient和LBFGS需要重复多次计算函数,因此你需要传入一个闭包去允许它们重新计算你的模型。这个闭包应当清空梯度, 计算损失,然后返回。
例子:
for input, target in dataset:
def closure():
optimizer.zero_grad()
output = model(input)
loss = loss_fn(output, target)
loss.backward()
return loss
optimizer.step(closure)
所有的优化都继承torch.optim.Optimizer类
CLASS torch.optim.Optimizer(params, defaults)
这是所有optimizer的基类。
参数:
params (iterable) —— Variable 或者 dict的iterable。指定了什么参数应当被优化。
defaults — (dict):包含了优化选项默认值的字典(一个参数组没有指定的参数选项将会使用默认值)。
方法:
add_param_group(param_group)
这个方法的作用是增加一个参数组,在fine tuning一个预训练的网络时有用。
load_state_dict(state_dict)
这个方法的作用是加载optimizer的状态
state_dict()
获取一个optimizer的状态(一个dict)。
zero_grad()方法用于清空梯度。
step(closure)用于进行单次更新。
1 torch.optim.SGD
class torch.optim.SGD(params, lr=<required parameter>, momentum=0, dampening=0, weight_decay=0, nesterov=False)
功能:
可实现SGD优化算法,带动量SGD优化算法,带NAG(Nesterov accelerated gradient)动量SGD优化算法,并且均可拥有weight_decay项。
参数:
params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
lr (float) – 学习率
momentum (float, 可选) – 动量因子(默认:0)
weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认:0)
dampening (float, 可选) – 动量的抑制因子(默认:0)在源码中是这样用的:buf.mul_(momentum).add_(1 - dampening, d_p),值得注意的是,若采用nesterov,dampening必须为 0.
nesterov (bool, 可选) – 使用Nesterov动量(默认:False)
注意事项:
pytroch中使用SGD十分需要注意的是,更新公式与其他框架略有不同!
pytorch中是这样的:
v = ρ ∗ v + g p = p − l r ∗ v = p − l r ∗ ρ ∗ v − l r ∗ g v=ρ∗v+g\ p=p−lr∗v = p - lr∗ρ∗v - lr∗g v=ρ∗v+gp=p−lr∗v=p−lr∗ρ∗v−lr∗g
其他框架:
v = ρ ∗ v + l r ∗ g p = p − v = p − ρ ∗ v − l r ∗ g v=ρ∗v+lr∗g\ p=p−v = p - ρ∗v - lr∗g v=ρ∗v+lr∗gp=p−v=p−ρ∗v−lr∗g
ρ是动量,v是速率,g是梯度,p是参数,其实差别就是在ρ∗v这一项,pytorch中将此项也乘了一个学习率。
手写sgd
def sgd_update(parameters, lr):
for param in parameters:
param.data = param.data - lr * param.grad.data
def sgd_momentum(parameters, vs, lr, gamma):
for param, v in zip(parameters, vs):
v[:] = gamma * v + lr * param.grad.data
param.data = param.data - v
loss.backward()
sgd_momentum(net.parameters(), vs, 1e-2, 0.9) # 使用的动量参数为 0.9,学习率 0.01
2 torch.optim.ASGD
class torch.optim.ASGD(params, lr=0.01, lambd=0.0001, alpha=0.75, t0=1000000.0, weight_decay=0)
功能:
ASGD也成为SAG,均表示随机平均梯度下降(Averaged Stochastic Gradient Descent),简单地说ASGD就是用空间换时间的一种SGD,详细可参看论文:http://riejohnson.com/rie/stograd_nips.pdf
参数:
params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
lr (float, 可选) – (默认:1e-2)初始学习率,可按需随着训练过程不断调整学习率
lambd (float, 可选) – 衰减项(默认:1e-4)
alpha (float, 可选) – eta更新的指数(默认:0.75)
t0 (float, 可选) – 指明在哪一次开始平均化(默认:1e6)
weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
3 torch.optim.Rprop
class torch.optim.Rprop(params, lr=0.01, etas=(0.5, 1.2), step_sizes=(1e-06, 50))
功能:
实现Rprop优化方法(弹性反向传播)
参数:
params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
lr (float, 可选) – 学习率(默认:1e-2)
etas (Tuple[float, float], 可选) – 一对(etaminus,etaplis), 它们分别是乘法的增加和减小的因子(默认:0.5,1.2)
step_sizes (Tuple[float, float], 可选) – 允许的一对最小和最大的步长(默认:1e-6,50)
该优化方法适用于full-batch,不适用于mini-batch,因而在min-batch大行其道的时代里,很少见到。
4 torch.optim.Adagrad
classs torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0, initial_accumulator_value=0)
功能:
实现Adagrad优化方法(Adaptive Gradient),Adagrad是一种自适应优化方法,是自适应的为各个参数分配不同的学习率。这个学习率的变化,会受到梯度的大小和迭代次数的影响。梯度越大,学习率越小;梯度越小,学习率越大。缺点是训练后期,学习率过小,因为Adagrad累加之前所有的梯度平方作为分母。
参数:
params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
lr (float, 可选) – 学习率(默认: 1e-2)
lr_decay (float, 可选) – 学习率衰减(默认: 0)
weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0
手写 Adagrad:
def sgd_adagrad(parameters, sqrs, lr):
eps = 1e-10
for param, sqr in zip(parameters, sqrs):
sqr[:] = sqr + param.grad.data ** 2
div = lr / torch.sqrt(sqr + eps) * param.grad.data
param.data = param.data - div
# 在循环中更新参数
sgd_adagrad(net.parameters(), sqrs, 1e-2) # 学习率设为 0.01
5 torch.optim.Adadelta
class torch.optim.Adadelta(params, lr=1.0, rho=0.9, eps=1e-06, weight_decay=0)
功能:
实现Adadelta优化方法。Adadelta是Adagrad的改进。Adadelta分母中采用距离当前时间点比较近的累计项,这可以避免在训练后期,学习率过小。
参数:
params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
rho (float, 可选) – 用于计算平方梯度的运行平均值的系数(默认:0.9)
eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-6)
lr (float, 可选) – 在delta被应用到参数更新之前对它缩放的系数(默认:1.0)
weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
手写Adadelta
def adadelta(parameters, sqrs, deltas, rho):
eps = 1e-6
for param, sqr, delta in zip(parameters, sqrs, deltas):
sqr[:] = rho * sqr + (1 - rho) * param.grad.data ** 2
cur_delta = torch.sqrt(delta + eps) / torch.sqrt(sqr + eps) * param.grad.data
delta[:] = rho * delta + (1 - rho) * cur_delta ** 2
param.data = param.data - cur_delta
# 循环中更新参数
adadelta(net.parameters(), sqrs, deltas, 0.9) # rho 设置为 0.9
6 torch.optim.RMSprop
class torch.optim.RMSprop(params, lr=0.01, alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)
功能:
实现RMSprop优化方法(Hinton提出),RMS是均方根(root meam square)的意思。RMSprop和Adadelta一样,也是对Adagrad的一种改进。RMSprop采用均方根作为分母,可缓解Adagrad学习率下降较快的问题。并且引入均方根,可以减少摆动.
参数:
params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
lr (float, 可选) – 学习率(默认:1e-2)
momentum (float, 可选) – 动量因子(默认:0)
alpha (float, 可选) – 平滑常数(默认:0.99)
eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8)
centered (bool, 可选) – 如果为True,计算中心化的RMSProp,并且用它的方差预测值对梯度进行归一化
weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
手写rmsprop
def rmsprop(parameters, sqrs, lr, alpha):
eps = 1e-10
for param, sqr in zip(parameters, sqrs):
sqr[:] = alpha * sqr + (1 - alpha) * param.grad.data ** 2
div = lr / torch.sqrt(sqr + eps) * param.grad.data
param.data = param.data - div
loss.backward()
rmsprop(net.parameters(), sqrs, 1e-3, 0.9) # 学习率设为 0.001,alpha 设为 0.9
7 torch.optim.Adam(AMSGrad)
class torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)
功能:
实现Adam(Adaptive Moment Estimation))优化方法。Adam是一种自适应学习率的优化方法,Adam利用梯度的一阶矩估计和二阶矩估计动态的调整学习率。吴老师课上说过,Adam是结合了Momentum和RMSprop,并进行了偏差修正。
参数:
params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
lr (float, 可选) – 学习率(默认:1e-3)
betas (Tuple[float, float], 可选) – 用于计算梯度以及梯度平方的运行平均值的系数(默认:0.9,0.999)
eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8)
weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
amsgrad - 是否采用AMSGrad优化方法,asmgrad优化方法是针对Adam的改进,通过添加额外的约束,使学习率始终为正值。(AMSGrad,ICLR-2018 Best-Pper之一,《On the convergence of Adam and Beyond》)。
手写adam
def adam(parameters, vs, sqrs, lr, t, beta1=0.9, beta2=0.999):
eps = 1e-8
for param, v, sqr in zip(parameters, vs, sqrs):
v[:] = beta1 * v + (1 - beta1) * param.grad.data
sqr[:] = beta2 * sqr + (1 - beta2) * param.grad.data ** 2
v_hat = v / (1 - beta1 ** t)
s_hat = sqr / (1 - beta2 ** t)
param.data = param.data - lr * v_hat / torch.sqrt(s_hat + eps)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)
# 初始化梯度平方项和动量项
sqrs = []
vs = []
for param in net.parameters():
sqrs.append(torch.zeros_like(param.data))
vs.append(torch.zeros_like(param.data))
t = 1
# 开始训练
losses = []
idx = 0
for e in range(5):
train_loss = 0
for im, label in train_data:
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
net.zero_grad()
loss.backward()
adam(net.parameters(), vs, sqrs, 1e-3, t) # 学习率设为 0.001
t += 1
# 记录误差
train_loss += loss.data[0]
if idx % 30 == 0:
losses.append(loss.data[0])
idx += 1
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
8 torch.optim.Adamax
class torch.optim.Adamax(params, lr=0.002, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
功能:
实现Adamax优化方法。Adamax是对Adam增加了一个学习率上限的概念,所以也称之为Adamax。 Adam的一种基于无穷范数的变种
参数:
params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
lr (float, 可选) – 学习率(默认:2e-3)
betas (Tuple[float, float], 可选) – 用于计算梯度以及梯度平方的运行平均值的系数
eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8)
weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
9 torch.optim.SparseAdam
class torch.optim.SparseAdam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08)
功能:
针对稀疏张量的一种“阉割版”Adam优化方法。
only moments that show up in the gradient get updated, and only those portions of the gradient get applied to the parameters
参数:
params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
lr (float, 可选) – 学习率(默认:1e-3)
betas (Tuple[float, float], 可选) – 用于计算梯度以及梯度平方的运行平均值的系数
eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8)
10 torch.optim.LBFGS
class torch.optim.LBFGS(params, lr=1, max_iter=20, max_eval=None, tolerance_grad=1e-05, tolerance_change=1e-09, history_size=100, line_search_fn=None)
功能:
实现L-BFGS(Limited-memory Broyden–Fletcher–Goldfarb–Shanno)优化方法。L-BFGS属于拟牛顿算法。L-BFGS是对BFGS的改进,特点就是节省内存。
使用注意事项:
警告
这个optimizer不支持为每个参数单独设置选项以及不支持参数组(只能有一个)
警告
目前所有的参数不得不都在同一设备上。在将来这会得到改进。
注意
这是一个内存高度密集的optimizer(它要求额外的param_bytes * (history_size + 1) 个字节)。如果它不适应内存,尝试减小history size,或者使用不同的算法。
参数:
lr (float) – 学习率(默认:1)
max_iter (int) – 每一步优化的最大迭代次数(默认:20))
max_eval (int) – 每一步优化的最大函数评价次数(默认:max_iter * 1.25)
tolerance_grad (float) – 一阶最优的终止容忍度(默认:1e-5)
tolerance_change (float) – 在函数值/参数变化量上的终止容忍度(默认:1e-9)
history_size (int) – 更新历史的大小(默认:100)
什么是参数组 /param_groups?
optimizer通过param_group来管理参数组.param_group中保存了参数组及其对应的学习率,动量等等.所以我们可以通过更改param_group[‘lr’]的值来更改对应参数组的学习率.
下面有一个手动更改学习率的例子
# 有两个`param_group`即,len(optim.param_groups)==2
optim.SGD([
{'params': model.base.parameters()},
{'params': model.classifier.parameters(), 'lr': 1e-3}
], lr=1e-2, momentum=0.9)
#一个参数组
optim.SGD(model.parameters(), lr=1e-2, momentum=.9)
# 获得学习率
print('learning rate: {}'.format(optimizer.param_groups[0]['lr']))
print('weight decay: {}'.format(optimizer.param_groups[0]['weight_decay']))
如何调整学习率
torch.optim.lr_scheduler provides several methods to adjust the learning rate based on the number of epochs. torch.optim.lr_scheduler.ReduceLROnPlateau allows dynamic learning rate reducing based on some validation measurements.
PyTorch学习率调整策略通过torch.optim.lr_scheduler接口实现。PyTorch提供的学习率调整策略分为三大类,分别是
a. 有序调整:等间隔调整(Step),按需调整学习率(MultiStep),指数衰减调整(Exponential)和 余弦退火CosineAnnealing。
b. 自适应调整:自适应调整学习率 ReduceLROnPlateau。
c. 自定义调整:自定义调整学习率 LambdaLR。
第一类,依一定规律有序进行调整,这一类是最常用的,分别是等间隔下降(Step),按需设定下降间隔(MultiStep),指数下降(Exponential)和 CosineAnnealing。这四种方法的调整时机都是人为可控的,也是训练时常用到的。
第二类,依训练状况伺机调整,这就是 ReduceLROnPlateau 方法。该法通过监测某一指标的变化情况,当该指标不再怎么变化的时候,就是调整学习率的时机,因而属于自适应的调整。
第三类,自定义调整, Lambda。 Lambda 方法提供的调整策略十分灵活,我们可以为不同的层设定不同的学习率调整方法,这在 fine-tune 中十分有用,我们不仅可为不同的层设定不同的学习率,还可以为其设定不同的学习率调整策略,简直不能更棒!
scheduler.step()
scheduler.step()在一次循环中只能出现一次
调整学习律总结如下:
1 等间隔调整学习率 StepLR
等间隔调整学习率,调整倍数为 gamma 倍,调整间隔为 step_size。间隔单位是step。需要注意的是, step 通常是指 epoch,不要弄成 iteration 了。
torch.optim.lr_scheduler.StepLR(optimizer, step_size, gamma=0.1, last_epoch=-1)
参数:
step_size(int) - 学习率下降间隔数,若为 30,则会在 30、 60、 90…个 step 时,将学习率调整为 lr*gamma。
gamma(float)- 学习率调整倍数,默认为 0.1 倍,即下降 10 倍。
last_epoch(int)- 上一个 epoch 数,这个变量用来指示学习率是否需要调整。当last_epoch 符合设定的间隔时,就会对学习率进行调整。当为-1 时,学习率设置为初始值。
import torch
import torch.optim as optim
from torch.optim import lr_scheduler
from torchvision.models import AlexNet
import matplotlib.pyplot as plt
model = AlexNet(num_classes=2)
optimizer = optim.SGD(params=model.parameters(), lr=0.05)
# lr_scheduler.StepLR()
# Assuming optimizer uses lr = 0.05 for all groups
# lr = 0.05 if epoch < 30
# lr = 0.005 if 30 <= epoch < 60
# lr = 0.0005 if 60 <= epoch < 90
scheduler = lr_scheduler.StepLR(optimizer, step_size=30, gamma=0.1)
plt.figure()
x = list(range(100))
y = []
for epoch in range(100):
scheduler.step()
lr = scheduler.get_lr()
print(epoch, scheduler.get_lr()[0])
y.append(scheduler.get_lr()[0])
plt.plot(x, y)
2 按需调整学习率 MultiStepLR
按设定的间隔调整学习率。这个方法适合后期调试使用,观察 loss 曲线,为每个实验定制学习率调整时机。
torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones, gamma=0.1, last_epoch=-1)
参数:
milestones(list)- 一个 list,每一个元素代表何时调整学习率, list 元素必须是递增的。如 milestones=[30,80,120]
gamma(float) - 学习率调整倍数,默认为 0.1 倍,即下降 10 倍。
last_epoch(int )- 上一个 epoch 数,这个变量用来指示学习率是否需要调整。last_epoch 符合设定的间隔时,就会对学习率进行调整。当为-1 时,学习率设置为初始值。
# ---------------------------------------------------------------
# 可以指定区间
# lr_scheduler.MultiStepLR()
# Assuming optimizer uses lr = 0.05 for all groups
# lr = 0.05 if epoch < 30
# lr = 0.005 if 30 <= epoch < 80
# lr = 0.0005 if epoch >= 80
print()
plt.figure()
y.clear()
scheduler = lr_scheduler.MultiStepLR(optimizer, [30, 80], 0.1)
for epoch in range(100):
scheduler.step()
print(epoch, 'lr={:.6f}'.format(scheduler.get_lr()[0]))
y.append(scheduler.get_lr()[0])
plt.plot(x, y)
plt.show()
3 指数衰减调整学习率 ExponentialLR
按指数衰减调整学习率,调整公式:$ lr=lr∗gamma∗∗epoch $
torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma, last_epoch=-1)
参数:
gamma- 学习率调整倍数的底,指数为 epoch,即 gamma**epoch
last_epoch(int)- 上一个 epoch 数,这个变量用来指示学习率是否需要调整。当
last_epoch 符合设定的间隔时,就会对学习率进行调整。当为-1 时,学习率设置为初始
值。
scheduler = lr_scheduler.ExponentialLR(optimizer, gamma=0.9)
print()
plt.figure()
y.clear()
for epoch in range(100):
scheduler.step()
print(epoch, 'lr={:.6f}'.format(scheduler.get_lr()[0]))
y.append(scheduler.get_lr()[0])
plt.plot(x, y)
plt.show()
4 余弦退火调整学习率 CosineAnnealingLR
以余弦函数为周期,并在每个周期最大值时重新设置学习率。以初始学习率为最大学习率,以 2∗Tmax 为周期,在一个周期内先下降,后上升。
torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max, eta_min=0, last_epoch=-1)
参数:
T_max(int)- 一次学习率周期的迭代次数,即 T_max 个 epoch 之后重新设置学习率。
eta_min(float)- 最小学习率,即在一个周期中,学习率最小会下降到 eta_min,默认值为 0。
5 根据指标调整学习率 ReduceLROnPlateau
当某指标不再变化(下降或升高),调整学习率,这是非常实用的学习率调整策略。
例如,当验证集的 loss 不再下降时,进行学习率调整;或者监测验证集的 accuracy,当accuracy 不再上升时,则调整学习率。
torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode=‘min’, factor=0.1, patience=10, verbose=False, threshold=0.0001, threshold_mode=‘rel’, cooldown=0, min_lr=0, eps=1e-08)
参数:
mode(str)- 模式选择,有 min 和 max 两种模式, min 表示当指标不再降低(如监测loss), max 表示当指标不再升高(如监测 accuracy)。
factor(float)- 学习率调整倍数(等同于其它方法的 gamma),即学习率更新为 lr = lr * factor
patience(int)- 忍受该指标多少个 step 不变化,当忍无可忍时,调整学习率。
verbose(bool)- 是否打印学习率信息, print(‘Epoch {:5d}: reducing learning rate of group {} to {:.4e}.’.format(epoch, i, new_lr))
如果为true,则为每个更新将消息打印到stdout。默认值:false。
threshold_mode(str)- 选择判断指标是否达最优的模式,有两种模式, rel 和 abs。
当 threshold_mode == rel,并且 mode == max 时, dynamic_threshold = best * ( 1 +threshold );
当 threshold_mode == rel,并且 mode == min 时, dynamic_threshold = best * ( 1 -threshold );
当 threshold_mode == abs,并且 mode== max 时, dynamic_threshold = best + threshold ;
当 threshold_mode == rel,并且 mode == max 时, dynamic_threshold = best - threshold;
threshold(float)- 配合 threshold_mode 使用。
cooldown(int)- “冷却时间“,当调整学习率之后,让学习率调整策略冷静一下,让模型再训练一段时间,再重启监测模式。
min_lr(float or list)- 学习率下限,可为 float,或者 list,当有多个参数组时,可用 list 进行设置。
eps(float)- 学习率衰减的最小值,当学习率变化小于 eps 时,则不调整学习率。
optimizer = torch.optim.SGD(model.parameters(), args.lr,
momentum=args.momentum ,
weight_decay=args.weight_decay)
scheduler = ReducelROnPlateau(optimizer,'min')
for epoch in range( args.start epoch, args.epochs ):
train(train_loader , model, criterion, optimizer, epoch )
result_avg, loss_val = validate(val_loader, model, criterion, epoch)
# Note that step should be called after validate()
scheduler.step(loss_val )
6 自定义调整学习率 LambdaLR
为不同参数组设定不同学习率调整策略。调整规则为,
$lr=base_lr∗lmbda(self.last_epoch) $
fine-tune 中十分有用,我们不仅可为不同的层设定不同的学习率,还可以为其设定不同的学习率调整策略。
torch.optim.lr_scheduler.LambdaLR(optimizer, lr_lambda, last_epoch=-1)
参数:
lr_lambda(function or list)- 一个计算学习率调整倍数的函数,输入通常为 step,当有多个参数组时,设为 list.
last_epoch (int) – 上一个 epoch 数,这个变量用来指示学习率是否需要调整。当
last_epoch 符合设定的间隔时,就会对学习率进行调整。当为-1 时,学习率设置为初始
值。
ignored_params = list(map(id, net.fc3.parameters()))
base_params = filter(lambda p: id(p) not in ignored_params, net.parameters())
optimizer = optim.SGD([
{'params': base_params},
{'params': net.fc3.parameters(), 'lr': 0.001*100}], 0.001, momentum=0.9,weight_decay=1e-4)
# Assuming optimizer has two groups.
lambda1 = lambda epoch: epoch // 3
lambda2 = lambda epoch: 0.95 ** epoch
scheduler = LambdaLR(optimizer, lr_lambda=[lambda1, lambda2])
for epoch in range(100):
train(...)
validate(...)
scheduler.step()
print('epoch: ', i, 'lr: ', scheduler.get_lr())
输出:
epoch: 0 lr: [0.0, 0.1]
epoch: 1 lr: [0.0, 0.095]
epoch: 2 lr: [0.0, 0.09025]
epoch: 3 lr: [0.001, 0.0857375]
epoch: 4 lr: [0.001, 0.081450625]
epoch: 5 lr: [0.001, 0.07737809374999999]
epoch: 6 lr: [0.002, 0.07350918906249998]
epoch: 7 lr: [0.002, 0.06983372960937498]
epoch: 8 lr: [0.002, 0.06634204312890622]
epoch: 9 lr: [0.003, 0.0630249409724609]
为什么第一个参数组的学习率会是 0 呢? 来看看学习率是如何计算的。
第一个参数组的初始学习率设置为 0.001,
lambda1 = lambda epoch: epoch // 3,
第 1 个 epoch 时,由 lr = base_lr * lmbda(self.last_epoch),
可知道 lr = 0.001 (0//3) ,又因为 1//3 等于 0,所以导致学习率为 0。
第二个参数组的学习率变化,就很容易看啦,初始为 0.1, lr = 0.1 * 0.95^epoch ,当
epoch 为 0 时, lr=0.1 , epoch 为 1 时, lr=0.10.95。
step源码
在 PyTorch 中,学习率的更新是通过 scheduler.step(),而我们知道影响学习率的一个重要参数就是 epoch,而 epoch 与 scheduler.step()是如何关联的呢?这就需要看源码了。
def step(self, epoch=None):
if epoch is None:
epoch = self.last_epoch + 1
self.last_epoch = epoch
for param_group, lr in zip(self.optimizer.param_groups, self.get_lr()):
param_group['lr'] = lr
函数接收变量 epoch,默认为 None,当为 None 时, epoch = self.last_epoch + 1。从这里知道, last_epoch 是用以记录 epoch 的。上面有提到 last_epoch 的初始值是-1,因此,第一个 epoch 的值为 -1+1 =0。接着最重要的一步就是获取学习率,并更新。
由于 PyTorch 是基于参数组的管理方式,这里需要采用 for 循环对每一个参数组的学习率进行获取及更新。这里需要注意的是 get_lr(), get_lr()的功能就是获取当前epoch,该参数组的学习率。
这里以 StepLR()为例,介绍 get_lr(),请看代码:
def get_lr(self):
return [base_lr * self.gamma ** (self.last_epoch // self.step_size) for
base_lr in self.base_lrs]
由于 PyTorch 是基于参数组的管理方式,可能会有多个参数组,因此用 for 循环,返
回的是一个 list。 list 元素的计算方式为
base_lr * self.gamma ** (self.last_epoch // self.step_size)
在执行一次 scheduler.step()之后, epoch 会加 1,因此scheduler.step()要放在 epoch 的 for 循环当中执行。
学习率下降例子
import torch
from torch.optim import lr_scheduler
class TwoLayerNet(torch.nn.Module):
def __init__(self, D_in, H, D_out):
"""
In the constructor we instantiate two nn.Linear modules and assign them as
member variables.
"""
super(TwoLayerNet, self).__init__()
self.linear1 = torch.nn.Linear(D_in, H)
self.linear2 = torch.nn.Linear(H, D_out)
def forward(self, x):
"""
In the forward function we accept a Tensor of input data and we must return
a Tensor of output data. We can use Modules defined in the constructor as
well as arbitrary operators on Tensors.
"""
h_relu = self.linear1(x).clamp(min=0)
y_pred = self.linear2(h_relu)
return y_pred
N, D_in, H, D_out = 64, 1000, 100, 10
x = torch.randn(N, D_in)
y = torch.randn(N, D_out)
# Construct our model by instantiating the class defined above
model = TwoLayerNet(D_in, H, D_out)
criterion = torch.nn.MSELoss(reduction='sum')
optimizer = torch.optim.SGD(model.parameters(), lr=1e-3)
print('learning rate: {}'.format(optimizer.param_groups[0]['lr']))
print('weight decay: {}'.format(optimizer.param_groups[0]['weight_decay']))
# scheduler = lr_scheduler.StepLR(optimizer, step_size=50, gamma=0.5)
# scheduler = lr_scheduler.MultiStepLR(optimizer, [50, 100], 0.5)
gamma = 0.9
scheduler = lr_scheduler.ExponentialLR(optimizer, gamma=gamma)
for t in range(200):
# Forward pass: Compute predicted y by passing x to the model
y_pred = model(x)
# Compute and print loss
scheduler.step()
loss = criterion(y_pred, y)
if t %25 ==0:
print(t, loss.item())
print('t:',t, scheduler.get_lr()[0])
print('learning rate: {}'.format(optimizer.param_groups[0]['lr']))
print(1e-3*gamma**t)
# print('weight decay: {}'.format(optimizer.param_groups[0]['weight_decay']))
# Zero gradients, perform a backward pass, and update the weights.
optimizer.zero_grad()
loss.backward()
optimizer.step()
# scheduler.step() 在一次循环中只能出现一次
手动改学习率
# 一个参数组
#optimizer.param_groups 返回是一个list
#optimizer.param_groups[0]返回的是字典
optimizer.param_groups[0]['lr'] = 1e-5
# 多个参数组
def set_learning_rate(optimizer, lr):
for param_group in optimizer.param_groups:
param_group['lr'] = lr
优化器SGD如图所示,model.parameters()找出model中要训练的所有权重,在这里就是linear的权重w,lr是学习率,其它参数可参考官方文档。
本实例是批量数据处理,小伙伴们不要被optimizer = torch.optim.SGD(model.parameters(), lr = 0.01)误导了,以为见了SGD就是随机梯度下降。要看传进来的数据是单个的还是批量的。这里的x_data是3个数据,是一个batch,调用的PyTorch API是 torch.optim.SGD,但这里的SGD不是随机梯度下降,而是批量梯度下降。也就是说,梯度下降算法使用的是随机梯度下降,还是批量梯度下降,还是mini-batch梯度下降,用的API都是 torch.optim.SGD。
随机梯度下降,现在一般指mini-batch gradient descent,计算一个mini-batch的损失,迭代也是以一个批次为单位来更新权重。
第四步——训练
训练步骤:
前馈——反馈——更新
模型;求损失——求梯度——更新权重
for epoch in range(100):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
print(epoch, loss.item())
optimizer.zero_grad()
print(loss)
loss.backward() # 反向传播,计算梯度
optimizer.step() # update 参数,即更新w和b的值
4、本算法的反向传播,计算梯度是通过以下语句实现的:
loss.backward() # 反向传播,计算梯度
5、本算法的参数(w,b)更新,是通过以下语句实现的:
optimizer.step() # update 参数,即更新w和b的值
6、 每一次epoch的训练过程,总结就是
-
①前向传播,求y hat (输入的预测值)
-
②根据y_hat和y_label(y_data)计算loss
-
③反向传播 backward (计算梯度)
-
④根据梯度,更新参数
7、本实例是批量数据处理,小伙伴们不要被optimizer = torch.optim.SGD(model.parameters(), lr = 0.01)误导了,以为见了SGD就是随机梯度下降。要看传进来的数据是单个的还是批量的。这里的x_data是3个数据,是一个batch,调用的PyTorch API是 torch.optim.SGD,但这里的SGD不是随机梯度下降,而是批量梯度下降。也就是说,梯度下降算法使用的是随机梯度下降,还是批量梯度下降,还是mini-batch梯度下降,用的API都是 torch.optim.SGD。
8、torch.nn.MSELoss也跟torch.nn.Module有关,参与计算图的构建,torch.optim.SGD与torch.nn.Module无关,不参与构建计算图。
9、传送门 torch.nn.Linear的pytorch文档
import torch
# 1.准备数据集 2.设计模型
# 3.构造损失函数和优化器 4.训练周期(前馈、反馈、更新)
# 一、准备数据集
# prepare dataset
# x,y是矩阵,3行1列 也就是说总共有3个数据,每个数据只有1个特征
# 使用PyTorch中的Tensor类型构造数据集
x_data = torch.tensor([[1.0], [2.0], [3.0]]) # 二阶张量[3,1]
y_data = torch.tensor([[2.0], [4.0], [6.0]]) # 二阶张量[3,1]
#design model using class
"""
our model class should be inherit from nn.Module, which is base class for all neural network modules.
member methods __init__() and forward() have to be implemented
class nn.linear contain two member Tensors: weight and bias
class nn.Linear has implemented the magic method __call__(),which enable the instance of the class can
be called just like a function.Normally the forward() will be called
"""
# 二、设计模型
# 设计模型类
class LinearModel(torch.nn.Module): # 封装成类(固定模板格式
# 自动计算反向传播
def __init__(self): # 构造函数
super(LinearModel, self).__init__() # 调用父类的构造 (super: 父类)
# class torch.nn.Linear(in_features, out_features, bias=True) # 线性模型,参数:输入样本维度,输出样本维度(需相同),bias意为有无偏置量(默认为True)
# (1,1)是指输入x和输出y的特征维度,这里数据集中的x和y的特征都是1维的
# 该线性层需要学习的参数是w和b 获取w/b的方式分别是~linear.weight/linear.bias
self.linear = torch.nn.Linear(1, 1) # nn: Neural Network,神经网络中的组建,
# 构造对象 线性模型
# torch.nn.Linear 为PyTorch中的一个类,该语句意为构造对象
# linear 对象包括 权重w 和 偏置b,继承自Module,可自动进行反向传播
# torch.nn.Linear(in,out,bias=true)
#in: 输入的维度
#out:输出的维度
#bias: 布尔类型,是否需要偏置量,默认为True
def forward(self, x): #重写父类中forward函数
# 对象后加():可调用的对象
y_pred = self.linear(x)
# linear——可调用对象 linear(x), __call__函数
return y_pred
model = LinearModel() # 实例化线性模型,callable的(可被调用的)
# model也是一个可调用对象
# 三、构造损失函数和优化器
# construct loss and optimizer
# class torch.nn.MSELoss(size_average=True, reduce=True) # 损失函数,参数:是否需要求均值,求和时是否需要降维(不常用)
criterion = torch.nn.MSELoss(size_average = False) # 需要(y_hat, y)就能把损失求出来
# MSELoss类继承自Module,torch.nn.MSELoss,可调用,pytorch提供的MSE损失函数。
criterion = torch.nn.MSELoss(reduction = 'sum')
# class torch.optim.SGD(params, Ir=
# 参数:需要优化(求梯度)的参数,学习率
optimizer = torch.optim.SGD(model.parameters(), lr = 0.01) # model.parameters()自动完成参数的初始化操作
# 实例化一个优化器对象,parameters是所有权重参数
# parameters检查模型中的所有成员
#SGD类的实例化
#optimizer = torch.optim.Adagrad(model.parameters(),lr=0.9)
#optimizer = torch.optim.Adam(model.parameters(),lr=0.05)
#optimizer = torch.optim.ASGD(model.parameters(),lr=0.01)
#optimizer = torch.optim.RMSprop(model.parameters(),lr=0.01)
#optimizer = torch.optim.Rprop(model.parameters(),lr=0.01)
#optimizer = torch.optim.Adamax(model.parameters(),lr=0.05)
#optimizer = torch.optim.LBFGS(model.parameters(),lr=0.01) #使用该方法时,step()需传入closure参数
# 四、训练循环
# training cycle forward, backward, update
for epoch in range(100):
y_pred = model(x_data) # forward:predict # 先在前馈中算y_hat
loss = criterion(y_pred, y_data)
# loss计算出来是一个
# forward: loss # 然后算损失
print(epoch, loss.item()) # 输出loss时自动调用__str__(); 不会产生计算图,是安全的
optimizer.zero_grad() # the grad computer by .backward() will be accumulated. so before backward, remember set the grad to zero
# 把所有参数的梯度都归零
# 将梯度值清0
#注意.backward()时梯度会被累计,注意所有的权重设为0
loss.backward() # backward: autograd,自动计算梯度
# 反向传播
# 反向传播求梯度
optimizer.step() # update 参数,即更新w和b的值,根据梯度和设好的学习率进行更新
# 优化器 更新权重
# step()函数:更新Update,所有参数中包含的梯度,以及预先设置的学习率进行自动更新
# Output weight and bias
# 打印出最终的权重和偏置值
print('w = ', model.linear.weight.item()) # weight是矩阵,必须加.item()转化成具体的数值
#打印时选item,不然w是一个矩阵
print('b = ', model.linear.bias.item())
# Test Model
x_test = torch.tensor([[4.0]]) # 测试用的x值为1*1的矩阵
#输入1*1矩阵
y_test = model(x_test) #输出1*1矩阵
print('y_pred = ', y_test.data) # 输出结果y_hat也是1*1的矩阵
输出结果:
训练100次
0 98.40182495117188
1 43.944671630859375
2 19.69989585876465
3 8.904844284057617
4 4.09725284576416
5 1.955139398574829
6 0.9996451139450073
7 0.5724288821220398
8 0.38041266798973083
9 0.29312819242477417
10 0.25249233841896057
11 0.23264899849891663
12 0.22208736836910248
13 0.21568244695663452
14 0.21115213632583618
15 0.20748083293437958
16 0.20421543717384338
17 0.20115414261817932
18 0.19820722937583923
19 0.19533367455005646
20 0.1925153136253357
21 0.18974366784095764
22 0.18701456487178802
23 0.1843256652355194
24 0.18167637288570404
25 0.17906497418880463
26 0.1764913648366928
27 0.1739550679922104
28 0.1714550107717514
29 0.16899099946022034
30 0.16656218469142914
31 0.16416852176189423
32 0.16180922091007233
33 0.1594836264848709
34 0.15719163417816162
35 0.15493245422840118
36 0.15270602703094482
37 0.1505115032196045
38 0.14834828674793243
39 0.1462162435054779
40 0.14411482214927673
41 0.14204366505146027
42 0.14000234007835388
43 0.13799023628234863
44 0.1360073685646057
45 0.1340526044368744
46 0.13212603330612183
47 0.13022726774215698
48 0.12835551798343658
49 0.1265108287334442
50 0.12469252943992615
51 0.12290070950984955
52 0.12113433331251144
53 0.11939340829849243
54 0.11767756938934326
55 0.11598648130893707
56 0.1143193393945694
57 0.11267638206481934
58 0.11105718463659286
59 0.10946103930473328
60 0.10788789391517639
61 0.10633731633424759
62 0.10480908304452896
63 0.1033029556274414
64 0.1018182784318924
65 0.1003548800945282
66 0.09891268610954285
67 0.0974912941455841
68 0.09609004855155945
69 0.0947091281414032
70 0.09334800392389297
71 0.0920066088438034
72 0.09068424999713898
73 0.0893808901309967
74 0.08809630572795868
75 0.08683034777641296
76 0.0855824202299118
77 0.08435236662626266
78 0.0831402987241745
79 0.0819452777504921
80 0.0807676911354065
81 0.0796068087220192
82 0.0784628689289093
83 0.07733520120382309
84 0.0762237012386322
85 0.07512824237346649
86 0.07404865324497223
87 0.0729842483997345
88 0.07193547487258911
89 0.0709015429019928
90 0.06988275796175003
91 0.06887834519147873
92 0.06788860261440277
93 0.06691285967826843
94 0.06595124304294586
95 0.06500330567359924
96 0.06406918913125992
97 0.06314833462238312
98 0.06224080175161362
99 0.061346251517534256
w = 1.8351130485534668
b = 0.37482669949531555
y_pred = tensor([[7.7153]])
总结整个过程:
import torch
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[2.0], [4.0], [6.0]])
class LinearModel(torch.nn.Module):
def __init__(self):
super(LinearModel, self).__init__()
self.linear = torch.nn.Linear(1, 1)
def forward(self, x):
y_pred = self.linear(x)
return y_pred
model = LinearModel()
criterion = torch.nn.MSELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
for epoch in range(1000):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
print("epoch:",epoch,"loss:",loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
print("**************test***************")
print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('when x = 4, y_pred = ',y_test.data)
在线性回归尝试不同的优化器
• torch.optim.Adagrad
• torch.optim.Adam
• torch.optim.Adamax
• torch.optim.ASGD
• torch.optim.LBFGS #error,解决中
• torch.optim.RMSprop
• torch.optim.Rprop
• torch.optim.SGD
补充类、对象、调用参数/对象等相关知识
class Foobar:
def __int__(self): # 构造函数
pass
def __call__(self, *args, **kwargs): # 使对象可调用
print("Hello" + str(args[0]))
foobar = Foobar() # 实例化
foobar(1, 2, 3) # 调用对象
## 补充知识:
函数里进行参数传递时,调用函数不确定输入参数是多少个时,就用*args,**kwargs来代替,*args代表元组,**kwargs代表字典。
def func(*args, **kwargs):
print(args) # 可变(普通/位置)参数传递:(1, 2, 3, 4) 元组
print(kwargs) # 关键字参数传递:{'x': 3, 'y': 5} 词典
#调用
func(1, 2, 3, 4, x=3, y=5)
#输出
> (1,2,3,4) #元组,args
> {'x':3,'y':5} #字典,kargs
我尝试了很多种优化器的使用,包括 SGD,Adagrad ,Adam ,ASGD, RMSprop ,Rprop,Adamax,以及LBFGS,