Matlab求解优化问题-Optimization Toolbox

提纲

• 1.前言
• 2.模型和代码

1.前言

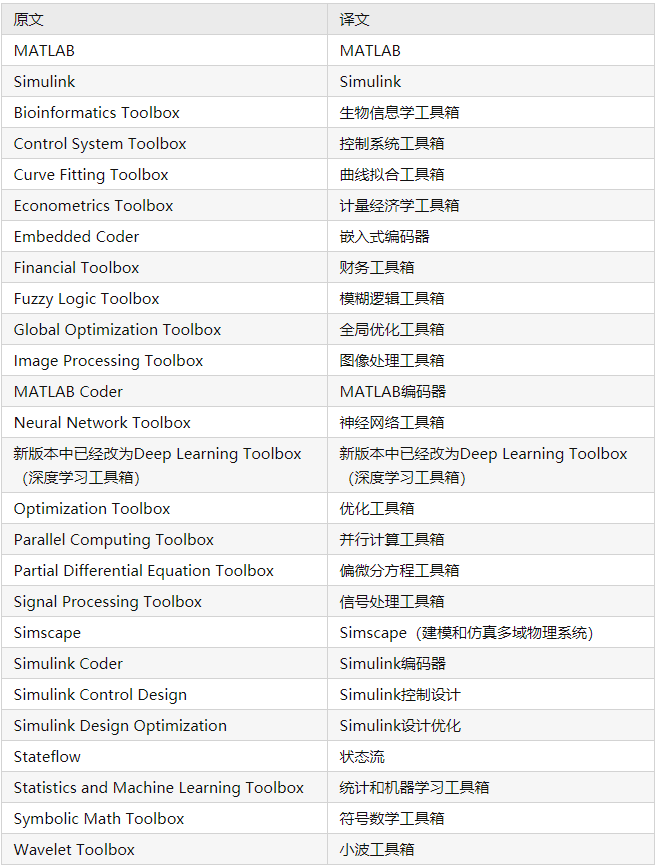
       前述文章建立的数学模型（），虽然写Lingo代码很简单。但是！！！Lingo求解速度很慢，电脑跑了1天也没结果。于是，只能转战Matlab（无奈），原因自然是Matlab功能非常强大。Matlab常用的工具箱如表1。关于Matlab的安装，本人使用的是学校购买了版权的Matlab,在此不对安装过程进行赘述。

表1 Matlab常用工具箱

       进入正题。Matlab中用于优化求解的主要是Optimization Toolbox工具箱，获取工具箱步骤为：

• 主页-附加功能-获取附加功能-搜索“Optimization Toolbox"-登录-安装

       该工具箱带了不少函数用于求解规划问题，主要有：

• linprog函数，线性规划
• intlinprog函数，混合整数线性规划
• fmincon函数，非线性规划（非整数）
• fgoalattain函数，多目标问题
• fminsearch、fminunc，无约束极小
• quadprog函数，二次规划
• fminimax函数，寻找能够最小化一组目标函数最大值的点

附上官方文档说明：https://ww2.mathworks.cn/help/optim/index.html?s_tid=CRUX_lftnav

2.模型和代码

2.1 数据

       我们仍然以2011年高教社杯全国大学生数学建模竞赛Ｂ题—交警服务平台的设置与调度提供的数据为例进行建模与分析。

       数据介绍：该数据集给出了某个城市A城区的交通路口以及交巡警平台信息，包括路口位置、路线的起点和终点路口节点、路口节点的发案率（每个路口平均每天的发生报警案件数量）、交巡警平台所在路口节点以及出入各个区的路口节点。该城区有92个路口节点（记为1-92），20个交巡警路口平台（记为1-20）。

2.2 假设、符号

       此例子涉及的假设有：

• 交巡警警车在市区道路的行驶速度恒为60km/h（虽然现实并非如此）；
• 在报警事件发生时，交巡警应尽量在3分钟之内到达。

表2 符号定义表

符号	含义
m	交巡警服务平台个数，例子中m= 20
n	交通路口节点个数，例子中n= 92
v	交巡警警车在市区道路的行驶速度，v=60 km/h
$c{n}_j$	第j个节点事件发生率（每个路口平均每天的发生报警案件数量）
$x_{ij}$	第i个平台是否管辖第j个节点,0-1变量
$w_{ij}$	最短距离是否小于最长响应时间对应的距离，例子中为3km

注：已经使用python的networkx包all_pairs_dijkstra_path_length函数计算交巡警服务平台到各个路口节点的最短距离（此函数背后的算法是Dijkstra算法）。由于篇幅限制，有需要的朋友可发送“shortest_path_distance’到后台获取代码。

2.3 模型

       模型原则：尽量满足3分钟到达报警现场，对于一些特殊节点（所有平台都无法做到3分钟到达，也就是所有平台到该节点的最短距离都大于3km），安排离它们最近的服务平台管辖,以便尽快响应报警事件。

表2 特殊路口节点管辖安排

交通路口节点标号	归属的服务平台标号	最近距离（km）
28	15	4.75
29	15	5.70
38	16	3.41
39	2	3.68
61	7	4.19
92	20	3.60

       接下来，我们以最大工作量与最小工作量之差最小化为目标建立数学模型，具体模型如下：
       接下来，我们以最大工作量与最小工作量之差最小化为目标建立数学模型，具体模型如下：
       $minz=max(q_i)-min(q_i)(1)$
       $s.t.q_i={\sum }_{j=1}^n{x}_{ij}c{n}_j,i\in I_1(2)$
       $x_{15,28}=x_{15,29}=x_{16,38}=x_{2,39}=x_{7,61}=x_{20,92}=1(3)$
       ${\sum }_{i=1}^m{x}_{ij}=1,j\in J_1(4)$
       ${\sum }_{i=1}^m{w}_{ij}{x}_{ij}=1,j\notin (28,29,38,39,61,92)(5)$
       $x_{ij}=0或1,i\in I_1,j\in J_1(6)$
       $I_1=1,2,...,20(7)$
       $J_1=1,2,...,92(8)$

      约束（2）计算i平台的工作量，式子（3）记录特殊节点的分配结果，式子（4）保证每个路口j都有其管辖的平台，式子（5）保证非特殊交通路口节点能被其管辖平台3分钟到达，式子（6）说明$x_{ij}$为0-1变量。

2.4 代码

      由于本文主要是介绍fmincon的用法，因此对于上述模型，放弃$x_{ij}$为0-1变量约束。

2.4.1 fmincon函数介绍

• 问题

• fmincon输入：
  • x = fmincon(fun,x0,A,b)
  • x = fmincon(fun,x0,A,b,Aeq,beq)
  • x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
  • x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
  • x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
  • x = fmincon(problem)
  • fun为目标函数，x0为决策变量初始值；nonlcon为非线性不等式或等式约束，options则是定义求解的一些具体参数，一般使用默认的就好。
  • options的文档：https://ww2.mathworks.cn/help/optim/ug/optim.problemdef.optimizationproblem.optimoptions.html
• 输出：
  • x=fmincon()
  • [x,fval] = fmincon(___)
  • [x,fval,exitflag,output] = fmincon(___)
  • [x,fval,exitflag,output,lambda,grad,hessian] = fmincon(___)
  • x为最优值，fval为取得最优值的决策变量值，exitflag为fmincon 的退出条件的值，output为优化过程信息的结构体

2.4.2 其他Matlab知识

• 读取外部文档

opts1 = detectImportOptions(‘C:\Users\xxx\Desktop\crimedata.xls’);%使用一个变量创建SpreadsheetImportOptions 对象
opts1.Sheet = ‘sheet1’;%读取的sheet_name
opts1.SelectedVariableNames=[2];%读取指定列，此处为读取第2列
opts1.DataRange= ‘2:93’;%读取指定列
cn_j=readmatrix(‘C:\Users\xxx\Desktop\crimedata.xls’,opts1);%读取cn矩阵

• 矩阵

1.矩阵创建
q_i=zeros(4,m)$\ast$nan;%创建一个全为nan值的4$\ast$m的矩阵
q_i=zeros(4,m);%%创建一个全为0的4$\ast$m的矩阵
q_i=ones(4,m);%%创建一个全为1的4$\ast$m的矩阵
2.矩阵元素提取
q_i(i,j);%提取矩阵的i行j列的元素
q_i([1,3],：);%提取矩阵的1、3行
q_i(：,1:3);%提取矩阵的1、2、3列
q_i(：,[1,3]);%提取矩阵的1、3列
3.矩阵处理，包括求和、删除、合并等操作
sum(q_i,1);%对整个矩阵按列求和，结果为1$\ast$m矩阵；2是按行求和，结果为1*4的矩阵
删除某行某列，直接让某行或某列为[]
Aeq_3(all(Aeq_3==0,2) = [];%去掉矩阵中的全0行
Q=[q_1;q_2;q_3];%合并矩阵,行数变化

2.4.3 代码示例

• 首先创建目标函数文件

function z=objective(x_ij)
opts1 = detectImportOptions('C:\Users\xxx\Desktop\crimedata.xls');%使用一个变量创建SpreadsheetImportOptions对象
opts1.Sheet = 'sheet1';%读取的sheet_name
opts1.SelectedVariableNames=[2];%读取指定列，此处为读取第2列
opts1.DataRange= '2:93';%读取行
cn_j=readmatrix('C:\Users\xxx\Desktop\crimedata.xls',opts1);%读取cn矩阵

m=20;
n=92;
q_i=zeros(1,m)*nan;%创建空矩阵
for i=1:m
    sum=0;
    for j=1:n
        sum=sum+x_ij((i-1)*n+j)*cn_j(j);
    end
    q_i(i)=sum;
end
z=max(q_i)-min(q_i);
end

• 使用fmincon函数

clear
%建立特殊节点的系数矩阵，命名为Aeq_1,6行
c1=zeros(1,1840);
c1(14*92+28)=1;
c2=zeros(1,1840);
c2(14*92+29)=1;
c3=zeros(1,1840);
c3(15*92+38)=1;
c4=zeros(1,1840);
c4(1*92+39)=1;
c5=zeros(1,1840);
c5(6*92+61)=1;
c6=zeros(1,1840);
c6(19*92+92)=1;
Aeq_1=[c1;c2;c3;c4;c5;c6];
%建立每个节点都被1个路口管辖约束的系数矩阵,命名为Aeq_2,应该有92行
Aeq_2=zeros(92,1840);
for j=1:92
    for i=0:19
        Aeq_2(j,i*92+j)=1;
    end
end
%建立非特殊节点都被管辖平台在3km之内到达约束的系数矩阵,命名为Aeq_3,应该有92-6=86行
%读取wij数据
opts = detectImportOptions('C:\Users\xxx\Desktop\distance.xls');%使用一个变量创建 SpreadsheetImportOptions 对象
opts.Sheet = 'sheet3';%读取的sheet_name
opts.SelectedVariableNames=[2:93];%读取指定列，此处为读取第2列到93列
opts.DataRange= '2:21';%读取行
w0=readmatrix('C:\Users\xxx\Desktop\distance.xls',opts);%读取w矩阵
w=zeros(1,1840);
for j=1:92
    for i=1:20
        w((i-1)*92+j)=w0(i,j);
    end
end
%w和Aeq_2相乘
Aeq_3=zeros(92,1840)*nan;
for j=1:92
    for i=0:19
        Aeq_3(j,i*92+j)=Aeq_2(j,i*92+j)*w(i*92+j);
    end
end 
Aeq_3(isnan(Aeq_3))=0;
%去掉矩阵中的全0行，其实是特殊节点对应的约束
Aeq_3(all(Aeq_3==0,2),:) = [];
%合并Aeq矩阵,92*2=184行
Aeq=[Aeq_1;Aeq_2;Aeq_3];

opts1 = detectImportOptions('C:\Users\xxx\Desktop\crimedata.xls');%使用一个变量创建 SpreadsheetImportOptions 对象
opts1.Sheet = 'sheet1';%读取的sheet_name
opts1.SelectedVariableNames=[2];%读取指定列，此处为读取第2列
opts1.DataRange= '2:93';
cn_j=readmatrix('C:\Users\xxx\Desktop\crimedata.xls',opts1);%读取cn矩阵
A_1=zeros(20,1840)*nan;
for i=1:20
    sum=0;
    for j=1:92
        sum=sum+Aeq_2(i,(i-1)*92+j)*cn_j(j);
    end
    A_1(i)=sum;
end 

%决策变量上下界
ub=ones(1,1840);
lb=zeros(1,1840);

%beq
beq=ones(184,1);

%初始化
x0=zeros(1,1840);
x0(14*92+28)=1;
x0(14*92+29)=1;
x0(15*92+38)=1;
x0(1*92+39)=1;
x0(6*92+61)=1;
x0(19*92+92)=1;
A=[];
b=[];
[x,fval]=fmincon(@(x)objective(x),x0,A,b,Aeq,beq,lb,ub);%声明传递的参数x，并且调用函数

提示：fmincon要求决策变量为一维的，如上述例子$x_{ij}$包含了9220=1840个变量，就必须定义一个11840的矩阵。稍微有点麻烦。