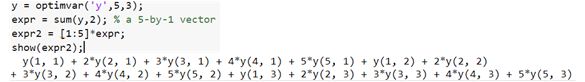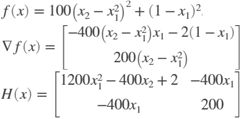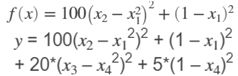matlab optimization toolbox 笔记

1 Introduction

matlab optimization 工具箱功能十分强大，这一章节梳理problem based optimization 和solver based optimization的问题。

Optimization Toolbox™ provides functions for finding parameters that minimize or maximize objectives while satisfying constraints. The toolbox includes solvers for linear programming (LP), mixed-integer linear programming (MILP), quadratic programming (QP), nonlinear programming (NLP), constrained linear least squares, nonlinear least squares, and nonlinear equations.

2 problem based optimization

2.1 workflow

prob = optimproblem('ObjectiveSense','maximize');                       % 1.定义最大值问题
x = optimvar('x',15,3,'Type','integer','LowerBound',0,'UpperBound',1);  % 2.定义状态变量
prob.Objective = sum(sum(f.*x));                                        % 3.定义目标函数
% 4.定义约束条件
onesum = sum(x,2) == 1;
vertsum = sum(x,1) <= 1;
prob.Constraints.onesum = onesum;
prob.Constraints.vertsum = vertsum;
% 5.变量初始化
x0.x = randn(size(x));  
x0.y = eye(4); % Assumes y is a 4-by-4 variable
% 6.求解器
sol = solve(prob);
% Or, for nonlinear problems,
sol = solve(prob,x0)

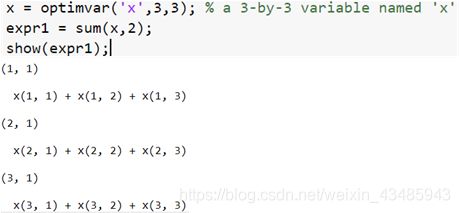
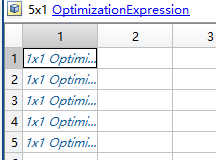
2.2 表达式

• 处理状态矩阵
  sum(x,1) 列向量之和，如果用sum(x)默认也是列向量之和
  
  sum(x,2)行向量之和
  
• expr满足矩阵运算规则。

expr = optimexpr; % 空表达式

• 约束方程
  约束方程都会自动转换成f(x)>=0或者f(x)<=0形式
  
• 通过函数式定义表达式

expr = fcn2optimexpr(@parameterfun,x,a,b,c);

2.3 变量设置

• 定义变量

x = optimvar('x',["United","Lufthansa","Virgin Air"]);
x("Lufthansa").LowerBound = 0;
x(1).LowerBound = -2;
showbounds(x)
show(x)
x

通过show(x)显示变量，通过showbounds(x)显示限制，还可以通过optimvar(‘x’,[“United”,“Lufthansa”,“Virgin Air”])对变量添加name indices。

2.4 求解器设置

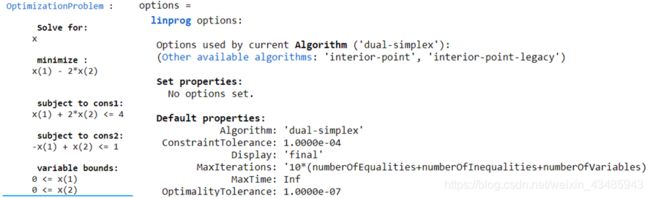
• 查看构建的optimization 问题和求解器

prob = optimproblem;
x = optimvar('x',2,'LowerBound',0);
prob.Objective = x(1) - 2*x(2);
prob.Constraints.cons1 = x(1) + 2*x(2) <= 4;
prob.Constraints.cons2 = -x(1) + x(2) <= 1;
show(prob)    %查看构建的optimization问题
options = optimoptions(prob)   % 查看使用的求解器

• optimoptions 设置

prob = optimproblem;
x = optimvar('x',2,'LowerBound',0);
prob.Objective = x(1) - 2*x(2);
prob.Constraints.cons1 = x(1) + 2*x(2) <= 4;
prob.Constraints.cons2 = -x(1) + x(2) <= 1;
show(prob)    %查看构建的optimization问题
options = optimoptions(prob)   % 查看使用的求解器
options.Display = 'iter';
sol = solve(prob,'Options',options,'Solver','quadprog');

2.5 查看计算结果的精度

通过fval误差的衡量指标，例如最小二乘问题，就是预测和实际的偏差平方。
exitflag 是一个字符，会提示求解情况

[sol,fval,exitflag,output,lambda] = solve(prob); % or
fval = evaluate(prob.Objective,sol)

3 solver based optimization

因为对主要的优化问题的算法并不是很熟悉，先关注workflow。

3.1 目标函数

目标函数有很多类型，这里主要关注标量类型。

• 通过matlab 脚本函数，定义优化问题的目标函数，好处是方便写目标函数的导数形式
  
  
  设置gradient能加快速度，提高精度。

% 在rosentwo.m中定义函数rosentwo
function [f,g,H] = rosentwo(x)
% Calculate objective f
f = 100*(x(2) - x(1)^2)^2 + (1-x(1))^2;

if nargout > 1 % gradient required
    g = [-400*(x(2)-x(1)^2)*x(1)-2*(1-x(1));
        200*(x(2)-x(1)^2)];
    if nargout > 2 % Hessian required
        H = [1200*x(1)^2-400*x(2)+2, -400*x(1);
            -400*x(1), 200];  
    end
end

如果要使用gradient，需要进行在options中进行设置

options = optimoptions(@fminunc,'Algorithm','trust-region',...
    'SpecifyObjectiveGradient',true);
[x fval] = fminunc(@rosentwo,[-1;2],options)

如果objective 比较复杂，需要使用hessian，需要在option中进行设置

options = optimoptions('fminunc','Algorithm','trust-region',...
    'SpecifyObjectiveGradient',true,'HessianFcn','objective');

• 匿名函数(Anonymous Function)，适合函数非常简单的情况

 anonrosen = @(x)(100*(x(2) - x(1)^2)^2 + (1-x(1))^2);
 

3.2 constraints

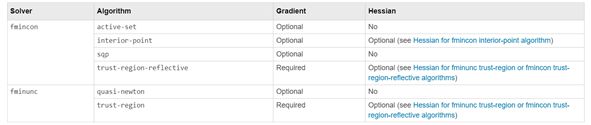
在matlab的几个主要的solver，使用非线性约束，用函数引用；使用线性约束，用线性矩阵Ax-b;使用变量bound，bl,bu;

x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)

• 非线性约束
  用函数引用。
  

% Step 1. 将约束函数和目标函数计算重复的内容单独提取出来
function [f1,c1,ceq1] = computeall(x)
    ceq1 = [];
    c1 = norm(x)^2 - 1;
    f1 = 100*(x(2) - x(1)^2)^2 + (1-x(1))^2;
    pause(1) % simulate expensive computation
end

% Step 2. 通过内嵌函数保留历史数值
function [x,f,eflag,outpt] = runobjconstr(x0,opts)
	if nargin == 1 % No options supplied
	    opts = [];
	end

	xLast = []; % Last place computeall was called
	myf = []; % Use for objective at xLast
	myc = []; % Use for nonlinear inequality constraint
	myceq = []; % Use for nonlinear equality constraint
	
	fun = @objfun; % the objective function, nested below
	cfun = @constr; % the constraint function, nested below
	
	% Call fmincon
	[x,f,eflag,outpt] = fmincon(fun,x0,[],[],[],[],[],[],cfun,opts);  %  fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)

    function y = objfun(x)
        if ~isequal(x,xLast) % Check if computation is necessary
            [myf,myc,myceq] = computeall(x);
            xLast = x;
        end
        % Now compute objective function
        y = myf + 20*(x(3) - x(4)^2)^2 + 5*(1 - x(4))^2;
    end

    function [c,ceq] = constr(x)
        if ~isequal(x,xLast) % Check if computation is necessary
            [myf,myc,myceq] = computeall(x);
            xLast = x;
        end
        % Now compute constraint functions
        c = myc; % In this case, the computation is trivial
        ceq = myceq;
    end
end

% step3: 统计算法所需要消耗的时间
opts = optimoptions(@fmincon,'Algorithm','interior-point','Display','off');
x0 = [-1,1,1,2];
tic
[x,fval,exitflag,output] = runobjconstr(x0,opts);
toc

% step4: 对比没有优化的方式
function y = myrosen2(x)
    f1 = computeall(x); % get first part of objective
    y = f1 + 20*(x(3) - x(4)^2)^2 + 5*(1 - x(4))^2;
end

function [c,ceq] = constr(x)
    [~,c,ceq] = computeall(x);
end

tic
[x,fval,exitflag,output] = fmincon(@myrosen2,x0,...
                   [],[],[],[],[],[],@constr,opts);
toc

3.3 设置options

• 如何设置

options = optimoptions(options,'StepTolerance',1e-10);
options.StepTolerance = 1e-10;
options = resetoptions(options,'StepTolerance');

• 重要参数
  

options = optimoptions(@fminunc,'Algorithm','trust-region',...
    'SpecifyObjectiveGradient',true); % 设置是否使用gradient

• 通过output函数，获取优化过程中的中间变量

function [history,searchdir] = runfmincon
 
% Set up shared variables with OUTFUN
history.x = [];
history.fval = [];
searchdir = [];
 
% call optimization
x0 = [-1 1];
options = optimoptions(@fmincon,'OutputFcn',@outfun,... 
    'Display','iter','Algorithm','active-set');
xsol = fmincon(@objfun,x0,[],[],[],[],[],[],@confun,options);
 
 function stop = outfun(x,optimValues,state)
     stop = false;
 
     switch state
         case 'init'
             hold on
         case 'iter'
         % Concatenate current point and objective function
         % value with history. x must be a row vector.
           history.fval = [history.fval; optimValues.fval];
           history.x = [history.x; x];
         % Concatenate current search direction with 
         % searchdir.
           searchdir = [searchdir;... 
                        optimValues.searchdirection'];
           plot(x(1),x(2),'o');
         % Label points with iteration number and add title.
         % Add .15 to x(1) to separate label from plotted 'o'
           text(x(1)+.15,x(2),... 
                num2str(optimValues.iteration));
           title('Sequence of Points Computed by fmincon');
         case 'done'
             hold off
         otherwise
     end
 end
 
 function f = objfun(x)
     f = exp(x(1))*(4*x(1)^2 + 2*x(2)^2 + 4*x(1)*x(2) +... 
                    2*x(2) + 1);
 end
 
 function [c, ceq] = confun(x)
     % Nonlinear inequality constraints
     c = [1.5 + x(1)*x(2) - x(1) - x(2);
         -x(1)*x(2) - 10];
     % Nonlinear equality constraints
     ceq = [];
 end
end