Matlab 最优化求解

matlab求解最优化函数主要包括linprog、quadprog、fminbnd、fmincon、fseminf和fminmax

1 线性规划

目标函数与约束条件都为线性函数，其Matlab标准式为
$$min{\mathbf{f}}^T\mathbf{x}$$

$$s.t.\{\begin{array}{l}\mathbf{A}\mathbf{x}\le \mathbf{b}\\ Aeq\cdot \mathbf{x}=beq\\ lb\le \mathbf{b}\le ub\end{array}$$

其中$\mathbf{A}、Aeq$表示分别为不等式与等式约束系数矩阵；$\mathbf{f},\mathbf{x},\mathbf{b},beq,lb,ub$为列向量。matlab求解代码为

[x,fval] = linprog(f,A,b,aeq,beq,lb,ub)

只能求出目标函数最小值，如果要求最大值，需要对目标函数转化

例1求解线性规划
$$\max z=2x_1+3x_2-5x_3$$

$$s.t.\{\begin{array}{l}{x}_1+x_2+x_3=7\\ 2x_1-5x_2+x_3\ge 10\\ x_1+3x_2+x_3\le 12\\ x_1,x_2,x_3\ge 0\end{array}$$

求解代码：

% 规划问题与matlab
%---------------------线性规划------------------
% 线性规划求解
% 例1
clc;clear;
f = [-2;-3;5]; %matlab的向量为列向量
a = [-2,5,-1; 1,3,1]; %系数矩阵
b = [-10,12]; %常数项
aeq = [1,1,1]; % 等式矩阵
beq = 7; %等式对应的常数向量
[x,y] = linprog(f,a,b,aeq,beq,zeros(3,1)) %zeros(3,1)解的下限都为正

例2 求解线性规划
$$\max z=3x_1-x_2-x_3$$

$$s.t.\{\begin{array}{l}{x}_1-2x_2+x_3\le 11\\ -4x_1+x_2+2x_3\ge 3\\ -2x_1+x_3=1\\ x_1,x_2,x_3\ge 0\end{array}$$

求解代码

clear;
f = [3;-1;-1];
a = [1,-2,1;4,-1,-2];
b = [11,-3];
aeq = [-2,0,1];
beq = 1;
[x,y] = linprog(-f,a,b,aeq,beq,zeros(3,1))

---

例3 （参数情形）求解线性规划
$$\max z=3x_1-x_2-x_3$$

$$s.t.\{\begin{array}{l}a{x}_1-2x_2+x_3\le 11\\ -4x_1+x_2+2x_3\ge 3\\ -2x_1+x_3=1\\ x_1,x_2,x_3\ge 0\end{array}$$

其中$0<a<10$

clear;
i = 0;
hold on
while i < 10
    f = [3;-1;-1];
    a = [i*1,-2,1;4,-1,-2];
    b = [11,-3];
    aeq = [-2,0,1];
    beq = 1;
    [x,y] = linprog(-f,a,b,aeq,beq,zeros(3,1));
    y = -y;
    plot(i,y,"*r");
    i = i + 0.05;
end
xlabel("参数");ylabel("目标函数值")
hold off

---

2 非线性规划

matlab非线性规划标准式
$$\min f(\mathbf{x})$$

$$s.t\{\begin{array}{l}\mathbf{A}\cdot \mathbf{x}\le \mathbf{b}\\ Aeq\cdot \mathbf{x}=beq\\ c(\mathbf{x})\le 0\\ ceq(\mathbf{x})=0\\ lb\le \mathbf{x}\le ub\end{array}$$

其中$c(\mathbf{x})$表示非线性不等式约束；$ceq(\mathbf{x})$表示非线性等式约束。matlab一般求解代码为

[x,fval] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

其中nonlcon是用M文件定义的非线性向量函数$c(\mathbf{x})$和$ceq(\mathbf{x})$，options为优化参数选项。

例4 求解非线性规划

M文件1:目标函数

function f = fun1(x);
% 非线性规划求解
% 目标函数
f = sum(x.^2)+8;
end

M文件2：非线性约束条件

function [g,h] = fun2(x,a)
% 非线性规划求解
% 目标函数
g = [-x(1)^2+x(2)-x(3)^2
    x(1)+x(2)^2+x(3)^3 - 20]; % 非线性不等式约束
h = [-x(1)-x(2)^2 + 2
    x(2)+2*x(3)^2 - 3];       % 非线性等式约束
end

% 调用fmincon函数
[x,y] = fmincon("fun1",rand(3,1),[],[],[],[],zeros(3,1),[],"fun2") 

---

3 无约束问题matlab解法

3.1 符号解

例5 求多元函数$f(x,y)=x^3-y^3+3x^2+3y^2-9x$

% 符号解
clc,clear;
% 符号变量定义
syms x y
f = x^3 - y^3 + 3*x^2 + 3*y^2 - 9*x;
% 求梯度
df = jacobian(f);
% 求hessian矩阵
d2f = jacobian(df);
% 求驻点
[xx,yy] = solve(df);
% 转双精度类型
xx = double(xx);yy = double(yy);

for i = 1:length(xx)
    % hessian矩阵
    a = subs(d2f,{x,y},{xx(i),yy(i)});
    % 特征值
    b = eig(a);
    f = subs(f,{x,y},{xx(i),yy(i)});
    if all(b > 0)
        fprintf("(%f,%f)是极小值点，对应极小值为% f\n",xx(i),yy(i),f);
    elseif all(b< 0)
        fprintf("(%f,%f)是极大值点，对应极大值为% f\n",xx(i),yy(i),f);
    elseif any(b>0) && any(b < 0)
        fprintf("(%f,%f)不是极值点\n",xx(i),yy(i));
    else 
        fprintf("无法判断(%f,%f)是极值点\n",xx(i),yy(i));
    end
end

---

3.2 数值解

例6 求多元函数$f(x,y)=x^3-y^3+3x^2+3y^2-9x$

% 数值解法解
clc,clear
% 定义匿名函数
f = @(x) x(1)^3 - x(2)^3 + 3*x(1)^2 + 3*x(2)^2 - 9*x(1);
g = @(x) -f(x);
% 求极小值点
[xy1,z1] = fminunc(f,rand(2,1))
% 求极大值点
[xy2,z2] = fminunc(g,rand(2,1));
xy2,z2 = -z2

利用数值方法可以加入梯度选项，编写M文件3

function [f,g] = fun3(x)
% 定义梯度
f = 100*(x(2) - x(1)^2)^2 + (1 - x(1))^2;
g = [-400*x(1)*(x(2) - x(1)^2) - 2*(1 - x(1));
    200*(x(2)-x(1)^2)];
end

调用函数fminunc

% 梯度法
options = optimset("GradObj","on");
[x,y] = fminunc("fun3",rand(1,2),options)

也可以加入Hessian矩阵信息，编写M文件4

function [f,g] = fun4(x)
% 定义函数
f = 100*(x(2) - x(1)^2)^2 + (1 - x(1))^2;
% 求梯度
df = [-400*x(1)*(x(2) - x(1)^2) - 2*(1 - x(1));
    200*(x(2)-x(1)^2)];
% 求Hessian矩阵
d2f = [-400*x(2)+1200*x(1)^2, -400*x(1)
    -400*x(1), 200];
end

调用fminsearch函数

% Hessian矩阵法
clc,clear
options = optimset("GradObj","on","Hessian","on");
[f,GRAD,HESS] = fminsearch("fun4",rand(1,2),options)

例7：求函数$f(x)=sin(x)+3$取极小值的$x$值

% 定义匿名函数
clc,clear
f = @(x) sin(x) + 3;
x0 = 2;
[x,y] = fminsearch(f,x0)

---

4 求解零点与方程组的解

4.1 多项式

例8 求解$f(x)=x^3-x^2+2x-3$的根

% 多项式系数(降幂)
xishu = [1 -1 2 -3];
x0 = roots(xishu)

---

4.2 符号解

% 符号解
syms x
x0 = solve(x^3 - x^2 + 2*x -3)
% 转化为小数格式,6位小数
x0 = vpa(x0,6)

---

4.3 数值解

% 数值解（仅求出实根）
clc,clear
y = @(x)x^3 - x^2 + 2*x -3;
x = fsolve(y,rand)

---

4.4 方程组情形

符号解

clc,clear
syms x y
[x,y] = solve(x^2+y-6,y^2+x-6)

数值解

f = @(x)[x(1)^2+x(2)-6,x(2)^2+x(1)-6];
% 只能求初始值需要在附近（局部）
xy = fsolve(f,rand(2,1))

---

5 约束问题matlab解法

5.1 二次规划

二次规划是指目标函数为二次函数但约束条件是线性的。matlab标准形式
$$\min \frac{1}{2}{\mathbf{x}}^T\mathbf{H}\mathbf{x}+{\mathbf{f}}^T\mathbf{x}$$

$$s.t.\{\begin{array}{l}\mathbf{A}\mathbf{x}\le \mathbf{b}\\ Aeq\cdot \mathbf{x}=beq\\ lb\le \mathbf{b}\le ub\end{array}$$

clc,clear
h = [4,-4;-4,8];
f = [-6;-3];
a = [1,1;4,1];
b = [3;9];
[x,value] = quadprog(h,f,a,b,[],[],zeros(2,1))

---

5.2 罚函数法（外）

利用罚函数可以将非线性约束规划转化为求解系列无约束极值问题。也称这种方法为SUMT方法.matlab标准问题
$$\min f(x)$$

$$s.t.\{\begin{array}{lc}{g}_i(x)\le 0& i=1,\dots ,r\\ h_j(x)\ge 0& j=1,\dots ,s\\ k_m(x)=0& m=1,\dots ,t\end{array}$$

设充分大$M>0$的数，构造罚函数
$$P(x,M)=f(x)+M\sum _{i=1}^{r}max(g_i(x),0)-M\sum _{j=1}^{s}min(h_j(x),0)+M\sum _{m=1}^t|k_m(x)|$$
例9求解非线性规划
$$\min f(x)=x_1^2+x_2^2+8$$

$$s.t\{\begin{array}{l}{x}_1^2-x_2\ge 0\\ -x_1-x_2^2+2=0\\ x_1,x_2\ge 0\end{array}$$

定义增广目标函数，编写M文件

function g = test1(x)
%罚函数构建
M = 50000;
f = x(1)^2+x(2)^2+8;
g = f-M*min(x(1),0)-M*min(x(2),0)-M*min(x(1)^2-x(2),0)+M*abs(-x(1)-x(2)^2+2);
end

调用函数fminunc

clc,clear
% 很难求出全局最优解，每次都是局部最优；每次结果存在差异
[x,y] = fminunc("test1",rand(2,1))

---

6 其他一些命令

6.1 fminbnd函数

用于求解单变量非线性函数在区间上的极小值，matlab格式命令

[x,fval] = fminbnd(fun,x1,x2,options)

例10 求函数$f(x)=(x-3{)}^2-1,x\in [0,5]$的最小值

clc,clear
f = @(x) (x-3)^2-1;
% 在区间（0，5）上的极小值
[x,y] = fminbnd(f,0,5)

---

6.2 fseminf函数

用于求标准问题
$$\begin{gathered} \min f(x) \\ s.t\{\begin{array}{l}\mathbf{A}\cdot \mathbf{x}\le \mathbf{b}\\ Aeq\cdot \mathbf{x}=beq\\ c(\mathbf{x})\le 0\\ ceq(\mathbf{x})=0\\ lb\le \mathbf{x}\le ub\\ K_i(\mathbf{x},w_i)\le 0,1\le i\le n\end{array} \end{gathered}$$
例11 求函数$f(x)=(x_1-0.5{)}^2+(x_2-0.5{)}^2+(x_3-0.5{)}^2$取最小值时$x$的值，约束条件
$$\{\begin{array}{l}{K}_1(x,w_1)=sin(w_1{x}_1)cos(w_1{x}_2)-\frac{1}{1000}(w_1-50{)}^2-sin(w_1{x}_3)-x_3\le 1\\ K_2(x,w_2)=sin(w_2{x}_2)cos(w_2{x}_1)-\frac{1}{1000}(w_2-50{)}^2-sin(w_2{x}_3)-x_3\le 1\\ 1\le w_1\le 100,1\le w_2\le 100\end{array}$$
编写目标函数M文件

function f = fun5(x,s)
% 目标函数
f = sum((x - 0.5).^2);
end

编写约束函数M文件

function [c,ceq,k1,k2,s] = fun6(x,s)
% 半无穷约束
c = [];ceq = [];
if isnan(s(1,1))
    s = [0.2,0;0.2,0];
end
% 取样值
w1 = 1:s(1,1):100;
w2 = 1:s(2,1):100;
% 半无穷约束
k1 = sin(w1*x(1)).*cos(w1*x(2))-1/1000*(w1-50).^2-sin(w1*x(3))-x(3)-1;
k2 = sin(w2*x(2)).*cos(w2*x(1))-1/1000*(w2-50).^2-sin(w2*x(3))-x(3)-1;
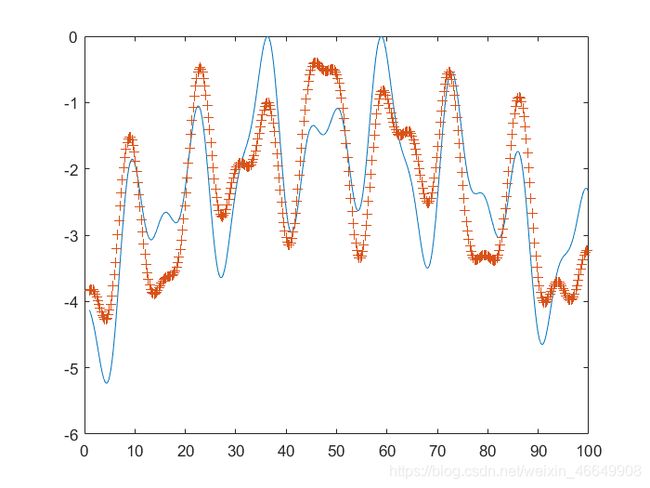
% 画出版无穷约束图形
figure(2)
plot(w1,k1,"-",w2,k2,"+")
end

调用函数fseminf

clc,clear
[x,y] = fseminf(@fun5,rand(3,1),2,@fun6)

---

6.3 fminimax函数

用于求解标准问题
$$\begin{gathered} \underset{x}{\min }\underset{i}{\max }{F}_i(x) \\ s.t\{\begin{array}{l}\mathbf{A}\cdot \mathbf{x}\le \mathbf{b}\\ Aeq\cdot \mathbf{x}=beq\\ c(\mathbf{x})\le 0\\ ceq(\mathbf{x})=0\\ lb\le \mathbf{x}\le ub\end{array} \end{gathered}$$
matlab命令为

[x,fval] = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

例11求解函数族$\{f_1(x),f_2(x),f_3(x),f_4(x),f_5(x)\}$取极小-极大值时$X$的值，其中
$$\{\begin{array}{l}{f}_1(x)=2x_1^2+x_2^2-48x_1-40x_2+304\\ f_2(x)=-x_1^2-3x_2^2\\ f_3(x)=x_1+3x_2-18\\ f_4(x)=-x_1-x_2\\ f_5(x)=x_1+x_2-8\end{array}$$
定义向量函数M文件

function f = fun7(x)
% 目标函数
f = [2*x(1)^2+x(2)^2-48*x(1)-40*x(2)+304
    -x(1)^2 - 3*x(2)^2
    x(1)+3*x(2)-18
    -x(1)-x(2)
    x(1)+x(2)-8];
end

调用函数fminimax

clc,clear
[x,y] = fminimax(@fun7,rand(2,1))

---

-END-

参考文献

司守奎等.数学建模算法与应用[M].国防工业出版社