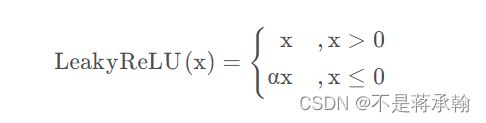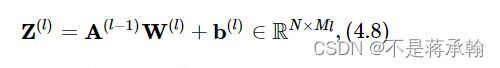HBU-NNDL 实验五 前馈神经网络（1）二分类任务

目录

4.1 神经元

4.1.1 净活性值

4.1.2 激活函数

4.2 基于前馈神经网络的二分类任务 

4.2.1 数据集构建

 4.2.2 模型构建

4.2.3 损失函数

4.2.4 模型优化

4.2.5 完善Runner类：RunnerV2_1

4.2.6 模型训练

equal – 张量比较

eq – 逐元素判断

拓展：eq_ – 将判断结果返回并替换原tensor

4.2.7 性能评价

【思考题】对比

心得体会：

参考链接：

---

4.1 神经元

        神经网络的基本组成单元为带有非线性激活函数的神经元。神经元是对生物神经元的结构和特性的一种简化建模，接收一组输入信号并产生输出。

        让我们来看一个经典的神经网络。这是一个包含三个层次的神经网络。红色的是输入层，绿色的是输出层，紫色的是中间层（也叫隐藏层）。输入层有3个输入单元，隐藏层有4个单元，输出层有2个单元。

4.1.1 净活性值

 使用Pytorch计算一组输入的净活性值。代码实现如下：

import torch

# 2个特征数为5的样本
X = torch.rand(size=[2, 5])

# 含有5个参数的权重向量
w = torch.rand(size=[5, 1])
# 偏置项
b = torch.rand(size=[1, 1])

# 使用'torch.matmul'实现矩阵相乘
z = torch.matmul(X, w) + b
print("input X:", X)
print("weight w:", w, "\nbias b:", b)
print("output z:", z)

input X: tensor([[0.5804, 0.6106, 0.6866, 0.7666, 0.5390],
        [0.4026, 0.2559, 0.3206, 0.7931, 0.5322]])
weight w: tensor([[0.3188],
        [0.7260],
        [0.5314],
        [0.6894],
        [0.5854]]) 
bias b: tensor([[0.2331]])
output z: tensor([[2.0703],
        [1.5759]])

我们也可以使用torch.nn.Linear完成输入张量的上述变换。

import torch

x = torch.randn(8, 3)  # 输入样本
fc = torch.nn.Linear(3, 5)  # 3为输入样本大小,5为输出样本大小
output = fc(x)
print('fc.weight.shape:\n ', fc.weight.shape, fc.weight)
print('fc.bias.shape:\n', fc.bias.shape)
print('output.shape:\n', output.shape)

ans = torch.mm(x, torch.t(fc.weight)) + fc.bias  # 计算结果与fc(x)相同
print('ans.shape:\n', ans.shape)

print(torch.equal(ans, output))

fc.weight.shape:
  torch.Size([5, 3]) 参数包含：
tensor([[ 0.3295, -0.0200, -0.0987],
        [-0.5065, 0.4210, 0.0575],
        [ 0.3568, 0.1998, 0.3935],
        [ 0.0994, 0.0568, 0.2794],
        [ 0.3297, -0.5719, 0.2750]], requires_grad=True)
fc.bias.shape:
 torch.Size([5])
output.shape:
 torch.Size([8, 5])
ans .shape:
 torch.Size([8, 5])
真

        首先，nn.linear(3,5)其权重的shape为（5，3），所以x与其相乘时，用torch.t求了nn.linear的转置，这样（83）（35）得到全连接层后的输出维度（85），结果也与fc(x)验证是一致的， torch.mm就是数学上的两个矩阵相乘。

4.1.2 激活函数

激活函数通常为非线性函数，可以增强神经网络的表示能力和学习能力。常用的激活函数有S型函数和ReLU函数。

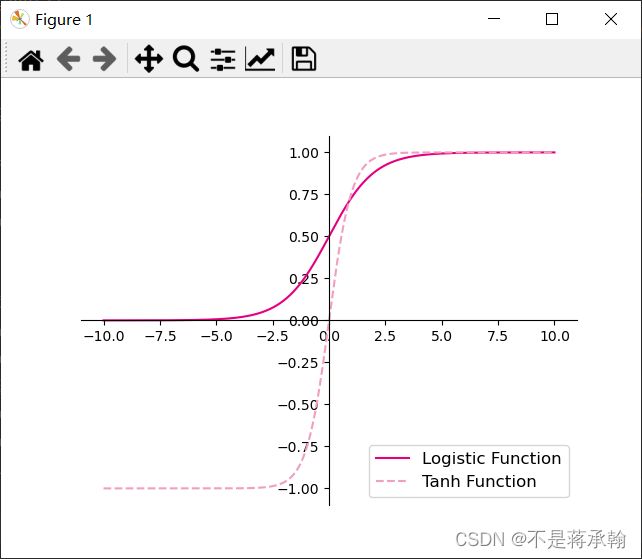
4.1.2.1 Sigmoid 型函数

import matplotlib.pyplot as plt
import torch

# Logistic函数
def logistic(z):
    return 1.0 / (1.0 + torch.exp(-z))

# Tanh函数
def tanh(z):
    return (torch.exp(z) - torch.exp(-z)) / (torch.exp(z) + torch.exp(-z))

# 在[-10,10]的范围内生成10000个输入值，用于绘制函数曲线
z = torch.linspace(-10, 10, 10000)

plt.figure()
plt.plot(z.tolist(), logistic(z).tolist(), color='#e4007f', label="Logistic Function")
plt.plot(z.tolist(), tanh(z).tolist(), color='#f19ec2', linestyle ='--', label="Tanh Function")

ax = plt.gca() # 获取轴，默认有4个
# 隐藏两个轴，通过把颜色设置成none
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
# 调整坐标轴位置   
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='lower right', fontsize='large')

plt.savefig('fw-logistic-tanh.pdf')
plt.show()

 

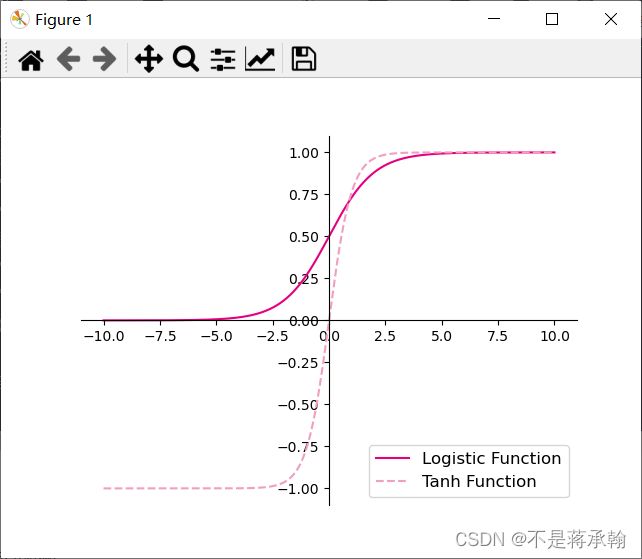
使用pytorch自带logistic（sigmoid）和tanh函数:

import torch
import matplotlib.pyplot as plt
# 在[-10,10]的范围内生成10000个输入值，用于绘制函数曲线
z = torch.linspace(-10, 10, 10000)

plt.figure()
plt.plot(z.tolist(), torch.sigmoid(z).tolist(), color='#e4007f', label="Logistic Function")
plt.plot(z.tolist(), torch.tanh(z).tolist(), color='#f19ec2', linestyle ='--', label="Tanh Function")

ax = plt.gca() # 获取轴，默认有4个
# 隐藏两个轴，通过把颜色设置成none
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
# 调整坐标轴位置
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='lower right', fontsize='large')

plt.savefig('fw-logistic-tanh.pdf')
plt.show()

 

 

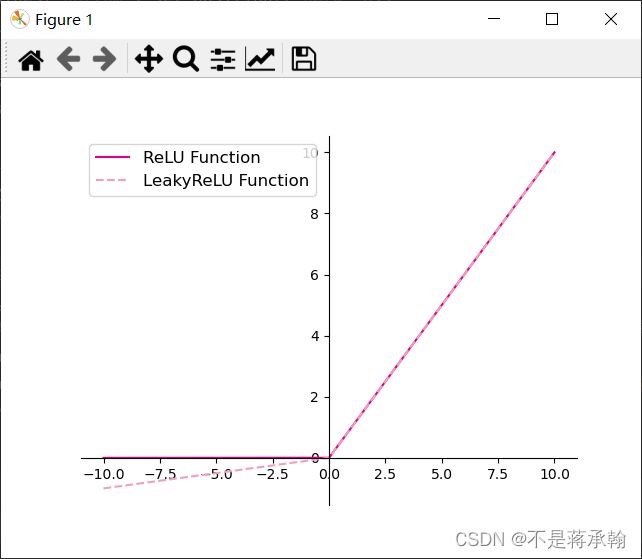
4.1.2.2 ReLU型函数

# ReLU
def relu(z):
    return torch.maximum(z, torch.tensor(0.))

# 带泄露的ReLU
def leaky_relu(z, negative_slope=0.1):
    # 当前版本torch暂不支持直接将bool类型转成int类型，因此调用了torch的cast函数来进行显式转换
    a1 = (torch.tensor((z > 0), dtype=torch.float32) * z)
    a2 = (torch.tensor((z <= 0), dtype=torch.float32) * (negative_slope * z))
    return a1 + a2

# 在[-10,10]的范围内生成一系列的输入值，用于绘制relu、leaky_relu的函数曲线
z = torch.linspace(-10, 10, 10000)

plt.figure()
plt.plot(z.tolist(), relu(z).tolist(), color="#e4007f", label="ReLU Function")
plt.plot(z.tolist(), leaky_relu(z).tolist(), color="#f19ec2", linestyle="--", label="LeakyReLU Function")

ax = plt.gca()
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='upper left', fontsize='large')
plt.savefig('fw-relu-leakyrelu.pdf')
plt.show()

 使用pytorch自带的relu和leaky_relu函数

import torch
import matplotlib.pyplot as plt
# 在[-10,10]的范围内生成10000个输入值，用于绘制函数曲线
z = torch.linspace(-10, 10, 10000)
plt.figure()
plt.plot(z.tolist(), torch.relu(z).tolist(), color='#e4007f', label="ReLU Function")
plt.plot(z.tolist(), torch.nn.functional.leaky_relu(z).tolist(), color='#f19ec2', linestyle ='--', label="LeakyReLU Function")

ax = plt.gca() # 获取轴，默认有4个
# 隐藏两个轴，通过把颜色设置成none
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
# 调整坐标轴位置
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='lower right', fontsize='large')

plt.savefig('fw-logistic-tanh.pdf')
plt.show()

可以看出nn自带函数库的LeakyReLU函数在x<0部分的斜率较小。 

 关于LeakyReLU函数，它是一种专门设计用于解决Dead ReLU问题的激活函数：

 Leaky ReLU函数的特点：

1、Leaky ReLU函数通过把x的非常小的线性分量给予负输入0.01x来调整负值的零梯度问题。
2、Leaky有助于扩大ReLU函数的范围，通常α的值为0.01左右。
3、Leaky ReLU的函数范围是负无穷到正无穷。
 

4.2 基于前馈神经网络的二分类任务 

前馈神经网络，是一种最简单的神经网络，各神经元分层排列，每个神经元只与前一层的神经元相连。接收前一层的输出，并输出给下一层，各层间没有反馈，是单向传播的。
在此神经网络中，各神经元可以接收前一层神经元的信号，并产生输出到下一层。第0层叫输入层，最后一层叫输出层，其他中间层叫做隐藏层。隐藏层可以是一层。也可以是多层。
 

前馈神经网络能够以任意精度逼近任意连续函数及平方可积函数．而且可以精确实现任意有限训练样本集。
其目标是拟合一个函数，如有一个分类器 y=f∗(x) 将输入 x 映射到输出类别 y 。深度前馈网络将这个映射定义为 f(x,θ) 并学习这个参数 θ 的值来得到最好的函数拟合。

 

4.2.1 数据集构建

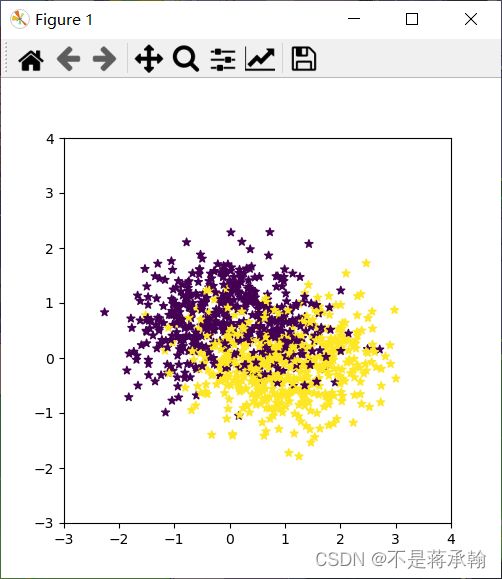
这里，我们使用第3.1.1节中构建的二分类数据集：Moon1000数据集，其中训练集640条、验证集160条、测试集200条。
该数据集的数据是从两个带噪音的弯月形状数据分布中采样得到，每个样本包含2个特征。

from nndl.dataset import make_moons

# 采样1000个样本
n_samples = 1000
X, y = make_moons(n_samples=n_samples, shuffle=True, noise=0.5)

num_train = 640
num_dev = 160
num_test = 200

X_train, y_train = X[:num_train], y[:num_train]
X_dev, y_dev = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
X_test, y_test = X[num_train + num_dev:], y[num_train + num_dev:]

y_train = y_train.reshape([-1,1])
y_dev = y_dev.reshape([-1,1])
y_test = y_test.reshape([-1,1])

plt.figure(figsize=(5,5))
plt.scatter(x=X[:, 0].tolist(), y=X[:, 1].tolist(), marker='*', c=y.tolist())
plt.xlim(-3,4)
plt.ylim(-3,4)
plt.savefig('linear-dataset-vis.pdf')
plt.show()

outer_circ_x.shape: torch.Size([500]) outer_circ_y.shape: torch.Size([500])
inner_circ_x.shape: torch.Size([500]) inner_circ_y.shape: torch.Size([500])
after concat shape: torch.Size([1000])
X shape: torch.Size([1000, 2])
y shape: torch.Size([1000])

 4.2.2 模型构建

为了更高效的构建前馈神经网络，我们先定义每一层的算子，然后再通过算子组合构建整个前馈神经网络。

4.2.2.1 线性层算子

公式（4.8）对应一个线性层算子，权重参数采用默认的随机初始化，偏置采用默认的零初始化。代码实现如下：

from nndl.op import Op


# 实现线性层算子
class Linear(Op):
    def __init__(self, input_size, output_size, name, weight_init=torch.randn, bias_init=torch.zeros):
        """
        输入：
            - input_size：输入数据维度
            - output_size：输出数据维度
            - name：算子名称
            - weight_init：权重初始化方式，默认使用'torch.randn'进行标准正态分布初始化
            - bias_init：偏置初始化方式，默认使用全0初始化
        """

        self.params = {}
        # 初始化权重
        self.params['W'] = weight_init(size=[input_size, output_size])
        # 初始化偏置
        self.params['b'] = bias_init(size=[1, output_size])
        self.inputs = None

        self.name = name

    def forward(self, inputs):
        """
        输入：
            - inputs：shape=[N,input_size], N是样本数量
        输出：
            - outputs：预测值，shape=[N,output_size]
        """
        self.inputs = inputs

        outputs = torch.matmul(self.inputs, self.params['W']) + self.params['b']
        return outputs

4.2.2.2 Logistic算子

本节我们采用Logistic函数来作为公式(4.9)中的激活函数。

这里也将Logistic函数实现一个算子，代码实现如下：

class Logistic(Op):
    def __init__(self):
        self.inputs = None
        self.outputs = None

    def forward(self, inputs):
        """
        输入：
            - inputs: shape=[N,D]
        输出：
            - outputs：shape=[N,D]
        """
        outputs = 1.0 / (1.0 + torch.exp(-inputs))
        self.outputs = outputs
        return outputs

4.2.2.3 层的串行组合

在定义了神经层的线性层算子和激活函数算子之后，我们可以不断交叉重复使用它们来构建一个多层的神经网络。

下面我们实现一个两层的用于二分类任务的前馈神经网络，选用Logistic作为激活函数，可以利用上面实现的线性层和激活函数算子来组装。代码实现如下：

# 实现一个两层前馈神经网络
class Model_MLP_L2(Op):
    def __init__(self, input_size, hidden_size, output_size):
        """
        输入：
            - input_size：输入维度
            - hidden_size：隐藏层神经元数量
            - output_size：输出维度
        """
        self.fc1 = Linear(input_size, hidden_size, name="fc1")
        self.act_fn1 = Logistic()
        self.fc2 = Linear(hidden_size, output_size, name="fc2")
        self.act_fn2 = Logistic()

    def __call__(self, X):
        return self.forward(X)

    def forward(self, X):
        """
        输入：
            - X：shape=[N,input_size], N是样本数量
        输出：
            - a2：预测值，shape=[N,output_size]
        """
        z1 = self.fc1(X)
        a1 = self.act_fn1(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn2(z2)
        return a2

测试一下

现在，我们实例化一个两层的前馈网络，令其输入层维度为5，隐藏层维度为10，输出层维度为1。
并随机生成一条长度为5的数据输入两层神经网络，观察输出结果。

# 实例化模型
model = Model_MLP_L2(input_size=5, hidden_size=10, output_size=1)
# 随机生成1条长度为5的数据
X = torch.rand(size=[1, 5])
result = model(X)
print ("result: ", result)

result:  tensor([[0.1737]])

4.2.3 损失函数

二分类交叉熵损失函数

# 实现交叉熵损失函数
class BinaryCrossEntropyLoss(Op):
    def __init__(self):
        self.predicts = None
        self.labels = None
        self.num = None

    def __call__(self, predicts, labels):
        return self.forward(predicts, labels)

    def forward(self, predicts, labels):
        """
        输入：
            - predicts：预测值，shape=[N, 1]，N为样本数量
            - labels：真实标签，shape=[N, 1]
        输出：
            - 损失值：shape=[1]
        """
        self.predicts = predicts
        self.labels = labels
        self.num = self.predicts.shape[0]
        loss = -1. / self.num * (torch.matmul(self.labels.t(), torch.log(self.predicts)) + torch.matmul((1-self.labels.t()), torch.log(1-self.predicts)))
        loss = torch.squeeze(loss, dim=1)
        return loss

4.2.4 模型优化

神经网络的参数主要是通过梯度下降法进行优化的，因此需要计算最终损失对每个参数的梯度。
由于神经网络的层数通常比较深，其梯度计算和上一章中的线性分类模型的不同的点在于：线性模型通常比较简单可以直接计算梯度，而神经网络相当于一个复合函数，需要利用链式法则进行反向传播来计算梯度。

4.2.4.1 反向传播算法

        反向传播是神经网络中最基本的学习算法，他是可以根据输出层的误差来更新每一层的参数。

        看了很多博客，说反向传播就是链式求导，这句话很好理解。可是我对这个生僻的词语还是很难产生一个形象的理解。阅读了大量博客后我知道这是一个学习算法，可以用来更新参数。有人把它跟逻辑回归的梯度下降做对比，把逻辑回归看做是一个没有隐层的神经网络。意思是说，“梯度下降”可以看做是“没有隐层的神经网络”的反向传播算法。这么说我不知道是不是准确，但是我对反向传播有了一个大致的理解了：“反向传播就是一个类似梯度下降的算法嘛。”

        可是用最普通的梯度下降不可以吗，梯度下降和反向传播有什么区别？这个写在心得体会里。

4.2.4.2 损失函数

实现损失函数的backward()，代码实现如下：

# 实现交叉熵损失函数
class BinaryCrossEntropyLoss(Op):
    def __init__(self, model):
        self.predicts = None
        self.labels = None
        self.num = None

        self.model = model

    def __call__(self, predicts, labels):
        return self.forward(predicts, labels)

    def forward(self, predicts, labels):
        """
        输入：
            - predicts：预测值，shape=[N, 1]，N为样本数量
            - labels：真实标签，shape=[N, 1]
        输出：
            - 损失值：shape=[1]
        """
        self.predicts = predicts
        self.labels = labels
        self.num = self.predicts.shape[0]
        loss = -1. / self.num * (torch.matmul(self.labels.t(), torch.log(self.predicts))
                                 + torch.matmul((1 - self.labels.t()), torch.log(1 - self.predicts)))

        loss = torch.squeeze(loss, dim=1)
        return loss

    def backward(self):
        # 计算损失函数对模型预测的导数
        loss_grad_predicts = -1.0 * (self.labels / self.predicts -
                                     (1 - self.labels) / (1 - self.predicts)) / self.num

        # 梯度反向传播
        self.model.backward(loss_grad_predicts)

4.2.4.3 Logistic算子

在本节中，我们使用Logistic激活函数，所以这里为Logistic算子增加的反向函数。

class Logistic(Op):
    def __init__(self):
        self.inputs = None
        self.outputs = None
        self.params = None

    def forward(self, inputs):
        outputs = 1.0 / (1.0 + torch.exp(-inputs))
        self.outputs = outputs
        return outputs

    def backward(self, grads):
        # 计算Logistic激活函数对输入的导数
        outputs_grad_inputs = torch.multiply(self.outputs, (1.0 - self.outputs))
        return torch.multiply(grads,outputs_grad_inputs)

4.2.4.4 线性层

class Linear(Op):
    def __init__(self, input_size, output_size, name, weight_init=torch.rand, bias_init=torch.zeros):
        self.params = {}
        self.params['W'] = weight_init(size=[input_size, output_size])
        self.params['b'] = bias_init(size=[1, output_size])

        self.inputs = None
        self.grads = {}

        self.name = name

    def forward(self, inputs):
        self.inputs = inputs
        outputs = torch.matmul(self.inputs, self.params['W']) + self.params['b']
        return outputs

    def backward(self, grads):
        """
        输入：
            - grads：损失函数对当前层输出的导数
        输出：
            - 损失函数对当前层输入的导数
        """
        self.grads['W'] = torch.matmul(self.inputs.T, grads)
        self.grads['b'] = torch.sum(grads, dim=0)

        # 线性层输入的梯度
        return torch.matmul(grads, self.params['W'].T)

4.2.4.5 整个网络

实现完整的两层神经网络的前向和反向计算。代码实现如下：

# 实现一个两层前馈神经网络
class Model_MLP_L2(Op):
    def __init__(self, input_size, hidden_size, output_size):
        # 线性层
        self.fc1 = Linear(input_size, hidden_size, name="fc1")
        # Logistic激活函数层
        self.act_fn1 = Logistic()
        self.fc2 = Linear(hidden_size, output_size, name="fc2")
        self.act_fn2 = Logistic()

        self.layers = [self.fc1, self.act_fn1, self.fc2, self.act_fn2]

    def __call__(self, X):
        return self.forward(X)

    # 前向计算
    def forward(self, X):
        z1 = self.fc1(X)
        a1 = self.act_fn1(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn2(z2)
        return a2

    # 反向计算
    def backward(self, loss_grad_a2):
        loss_grad_z2 = self.act_fn2.backward(loss_grad_a2)
        loss_grad_a1 = self.fc2.backward(loss_grad_z2)
        loss_grad_z1 = self.act_fn1.backward(loss_grad_a1)
        loss_grad_inputs = self.fc1.backward(loss_grad_z1)

4.2.4.6 优化器

在计算好神经网络参数的梯度之后，我们将梯度下降法中参数的更新过程实现在优化器中。

与第3章中实现的梯度下降优化器SimpleBatchGD不同的是，此处的优化器需要遍历每层，对每层的参数分别做更新。

from opitimizer import Optimizer

class BatchGD(Optimizer):
    def __init__(self, init_lr, model):
        super(BatchGD, self).__init__(init_lr=init_lr, model=model)

    def step(self):
        # 参数更新
        for layer in self.model.layers: # 遍历所有层
            if isinstance(layer.params, dict):
                for key in layer.params.keys():
                    layer.params[key] = layer.params[key] - self.init_lr * layer.grads[key]

4.2.5 完善Runner类：RunnerV2_1

基于3.1.6实现的 RunnerV2 类主要针对比较简单的模型。而在本章中，模型由多个算子组合而成，通常比较复杂，因此本节继续完善并实现一个改进版： RunnerV2_1类，其主要加入的功能有：

1. 支持自定义算子的梯度计算，在训练过程中调用self.loss_fn.backward()从损失函数开始反向计算梯度；
2. 每层的模型保存和加载，将每一层的参数分别进行保存和加载。

import os


class RunnerV2_1(object):
    def __init__(self, model, optimizer, metric, loss_fn, **kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric

        # 记录训练过程中的评估指标变化情况
        self.train_scores = []
        self.dev_scores = []

        # 记录训练过程中的评价指标变化情况
        self.train_loss = []
        self.dev_loss = []

    def train(self, train_set, dev_set, **kwargs):
        # 传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs", 0)
        # 传入log打印频率，如果没有传入值则默认为100
        log_epochs = kwargs.get("log_epochs", 100)

        # 传入模型保存路径
        save_dir = kwargs.get("save_dir", None)

        # 记录全局最优指标
        best_score = 0
        # 进行num_epochs轮训练
        for epoch in range(num_epochs):
            X, y = train_set
            # 获取模型预测
            logits = self.model(X)
            # 计算交叉熵损失
            trn_loss = self.loss_fn(logits, y)  # return a tensor

            self.train_loss.append(trn_loss.item())
            # 计算评估指标
            trn_score = self.metric(logits, y).item()
            self.train_scores.append(trn_score)

            self.loss_fn.backward()

            # 参数更新
            self.optimizer.step()

            dev_score, dev_loss = self.evaluate(dev_set)
            # 如果当前指标为最优指标，保存该模型
            if dev_score > best_score:
                print(f"[Evaluate] best accuracy performence has been updated: {best_score:.5f} --> {dev_score:.5f}")
                best_score = dev_score
                if save_dir:
                    self.save_model(save_dir)

            if log_epochs and epoch % log_epochs == 0:
                print(f"[Train] epoch: {epoch}/{num_epochs}, loss: {trn_loss.item()}")

    def evaluate(self, data_set):
        X, y = data_set
        # 计算模型输出
        logits = self.model(X)
        # 计算损失函数
        loss = self.loss_fn(logits, y).item()
        self.dev_loss.append(loss)
        # 计算评估指标
        score = self.metric(logits, y).item()
        self.dev_scores.append(score)
        return score, loss

    def predict(self, X):
        return self.model(X)

    def save_model(self, save_dir):
        # 对模型每层参数分别进行保存，保存文件名称与该层名称相同
        for layer in self.model.layers:  # 遍历所有层
            if isinstance(layer.params, dict):
                torch.save(layer.params, os.path.join(save_dir, layer.name + ".pdparams"))

    def load_model(self, model_dir):
        # 获取所有层参数名称和保存路径之间的对应关系
        model_file_names = os.listdir(model_dir)
        name_file_dict = {}
        for file_name in model_file_names:
            name = file_name.replace(".pdparams", "")
            name_file_dict[name] = os.path.join(model_dir, file_name)

        # 加载每层参数
        for layer in self.model.layers:  # 遍历所有层
            if isinstance(layer.params, dict):
                name = layer.name
                file_path = name_file_dict[name]
                layer.params = torch.load(file_path)

4.2.6 模型训练

基于RunnerV2_1，使用训练集和验证集进行模型训练，共训练2000个epoch。评价指标为第章介绍的accuracy。代码实现如下：

from metric import accuracy
torch.random.manual_seed(123)
epoch_num = 1000

model_saved_dir = "model"

# 输入层维度为2
input_size = 2
# 隐藏层维度为5
hidden_size = 5
# 输出层维度为1
output_size = 1

# 定义网络
model = Model_MLP_L2(input_size=input_size, hidden_size=hidden_size, output_size=output_size)

# 损失函数
loss_fn = BinaryCrossEntropyLoss(model)

# 优化器
learning_rate = 0.2
optimizer = BatchGD(learning_rate, model)

# 评价方法
metric = accuracy

# 实例化RunnerV2_1类，并传入训练配置
runner = RunnerV2_1(model, optimizer, metric, loss_fn)

runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=epoch_num, log_epochs=50, save_dir=model_saved_dir)

[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.61250
[Train] epoch: 0/1000, loss: 0.6397520899772644
[Evaluate] best accuracy performence has been updated: 0.61250 --> 0.63125
[Evaluate] best accuracy performence has been updated: 0.63125 --> 0.66875
[Evaluate] best accuracy performence has been updated: 0.66875 --> 0.70625
[Evaluate] best accuracy performence has been updated: 0.70625 --> 0.73125
[Evaluate] best accuracy performence has been updated: 0.73125 --> 0.76250
[Train] epoch: 50/1000, loss: 0.455339252948761
[Train] epoch: 100/1000, loss: 0.4276913106441498
[Train] epoch: 150/1000, loss: 0.41676321625709534
[Train] epoch: 200/1000, loss: 0.41176411509513855
[Train] epoch: 250/1000, loss: 0.40923643112182617
[Train] epoch: 300/1000, loss: 0.40786704421043396
[Train] epoch: 350/1000, loss: 0.4070819318294525
[Train] epoch: 400/1000, loss: 0.40660473704338074
[Train] epoch: 450/1000, loss: 0.40629419684410095
[Train] epoch: 500/1000, loss: 0.40607523918151855
[Train] epoch: 550/1000, loss: 0.40590834617614746
[Train] epoch: 600/1000, loss: 0.4057714641094208
[Train] epoch: 650/1000, loss: 0.4056529700756073
[Train] epoch: 700/1000, loss: 0.4055461585521698
[Train] epoch: 750/1000, loss: 0.405447393655777
[Train] epoch: 800/1000, loss: 0.40535473823547363
[Train] epoch: 850/1000, loss: 0.4052668511867523
[Train] epoch: 900/1000, loss: 0.4051835238933563
[Train] epoch: 950/1000, loss: 0.4051033556461334

accuracy函数如下：

import torch


def accuracy(preds, labels):
    """
    输入：
        - preds：预测值，二分类时，shape=[N, 1]，N为样本数量，多分类时，shape=[N, C]，C为类别数量
        - labels：真实标签，shape=[N, 1]
    输出：
        - 准确率：shape=[1]
    """
    # 判断是二分类任务还是多分类任务，preds.shape[1]=1时为二分类任务，preds.shape[1]>1时为多分类任务
    if preds.shape[1] == 1:
        data_float = torch.randn(preds.shape[0], preds.shape[1])
        # 二分类时，判断每个概率值是否大于0.5，当大于0.5时，类别为1，否则类别为0
        # 使用'torch.cast'将preds的数据类型转换为float32类型
        preds = (preds>=0.5).type(torch.float32)
    else:
        # 多分类时，使用'torch.argmax'计算最大元素索引作为类别
        data_float = torch.randn(preds.shape[0], preds.shape[1])
        preds = torch.argmax(preds,dim=1, dtype=torch.int32)
    return torch.mean(torch.eq(preds, labels).type(torch.float32))

在模型训练中，score的值有可能一直为0，造成这种结果的原因是在accuracy函数的最后一行，

要将torch.equal改为torch.eq，上次实验就找这个bug找了好久。

equal – 张量比较

比较两个张量是否相等–相等返回：True; 否则返回：False

'''
		tensor调用equal方法与torch.equal是一致的
		都是比较两个张量是否相等
'''
x = torch.tensor([1, 2, 3])
y = torch.tensor([1, 1, 3])
print(x.equal(y))
print(x.equal(y) == torch.equal(x, y))

False
True

eq – 逐元素判断

比较两个张量中，每一个对应位置上元素是否相等–对应位置相等，就返回一个True；否则返回一个False.

import torch
'''
		逐元素进行判断是否相等
'''
x = torch.tensor([1, 2, 3])
y = torch.tensor([1, 1, 3])
print(x.eq(y))

tensor([ True, False,  True])

拓展：eq_ – 将判断结果返回并替换原tensor

等价于tensor = tensor.eq(other);
即：将比较后的结果替换原张量的值

import torch
x = torch.tensor([1, 2, 3])
y = torch.tensor([1, 1, 3])
print(x.eq_(y))
print(x)

tensor([1, 0, 1])
tensor([1, 0, 1])

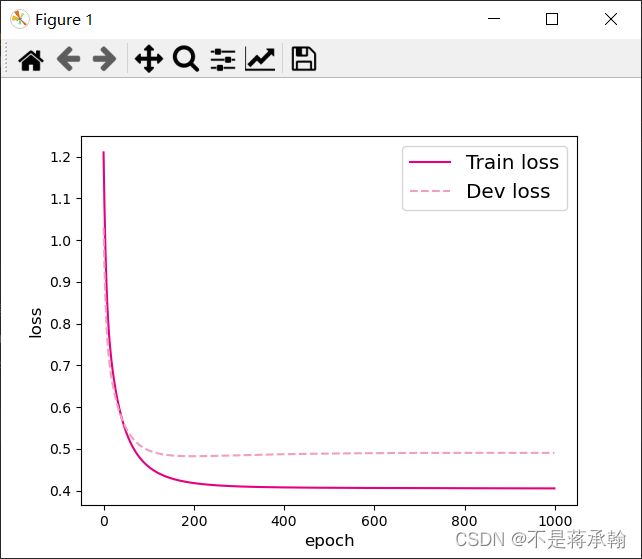
可视化观察训练集与验证集的损失函数变化情况。

# 打印训练集和验证集的损失
plt.figure()
plt.plot(range(epoch_num), runner.train_loss, color="#e4007f", label="Train loss")
plt.plot(range(epoch_num), runner.dev_loss, color="#f19ec2", linestyle='--', label="Dev loss")
plt.xlabel("epoch", fontsize='large')
plt.ylabel("loss", fontsize='large')
plt.legend(fontsize='x-large')
plt.show()

 

4.2.7 性能评价

# 加载训练好的模型
runner.load_model(model_saved_dir)
# 在测试集上对模型进行评价
score, loss = runner.evaluate([X_test, y_test])

print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))

[Test] score/loss: 0.8050/0.4815

将epoch=10000，lr=0.01

结果：

Train] epoch: 9800/10000, loss: 0.4132726788520813
[Train] epoch: 9850/10000, loss: 0.4131805896759033
[Train] epoch: 9900/10000, loss: 0.41309019923210144
[Train] epoch: 9950/10000, loss: 0.41300198435783386
[Test] score/loss: 0.7950/0.4848
 

将epoch=100000，lr=0.01

结果：

[Train] epoch: 99750/100000, loss: 0.38984251022338867
[Train] epoch: 99800/100000, loss: 0.38983020186424255
[Train] epoch: 99850/100000, loss: 0.389818012714386
[Train] epoch: 99900/100000, loss: 0.3898058831691742
[Train] epoch: 99950/100000, loss: 0.38979363441467285
[Test] score/loss: 0.7750/0.5800
 

可以看出epoch提高，训练loss降低，测试loss升高，模型欠拟合。

将epoch=10000，lr=0.001

结果：

Train] epoch: 9750/10000, loss: 0.5265558958053589
[Train] epoch: 9800/10000, loss: 0.5263811945915222
[Train] epoch: 9850/10000, loss: 0.5262061953544617
[Train] epoch: 9900/10000, loss: 0.5260314345359802
[Train] epoch: 9950/10000, loss: 0.5258569121360779
[Test] score/loss: 0.6550/0.5893

将lr调小，训练和测试loss都有提升，说明模型过拟合。

【思考题】对比

3.1 基于Logistic回归的二分类任务 4.2 基于前馈神经网络的二分类任务

谈谈自己的看法

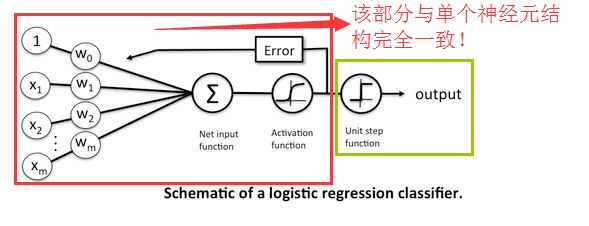
 Logistic回归就是神经网络的一个神经元，这也是为什么神经网络能处理更复杂问题的原因

下面看一个实例：

导包

import torch
import numpy as np
from torch import nn
from torch.autograd import Variable
import torch.nn.functional as F
import matplotlib.pyplot as plt

创建数据集：

#绘图_决策_边界
def plot_decision_boundary(model,x,y):
    #设置最小值和最大值，并给它一些空白
    x_min,x_max=x[:,0].min()-1,x[:,0].max()+1
    y_min,y_max=x[:,1].min()-1,x[:,1].max()+1
    h=0.01
    #生成点的网格，点之间的距离为h
    xx,yy=np.meshgrid(np.arange(x_min,x_max,h),np.arange(y_min,y_max,h))
    #Predict the function value for the whole grid
    z=model(np.c_[xx.ravel(),yy.ravel()])
    z=z.reshape(xx.shape)
    #绘制等高线和训练示例
    plt.contourf(xx,yy,z,cmap=plt.cm.Spectral)
    plt.ylabel('x2')
    plt.xlabel('x1')
    plt.scatter(x[:,0],x[:,1],c=y.reshape(-1),s=40,cmap=plt.cm.Spectral)

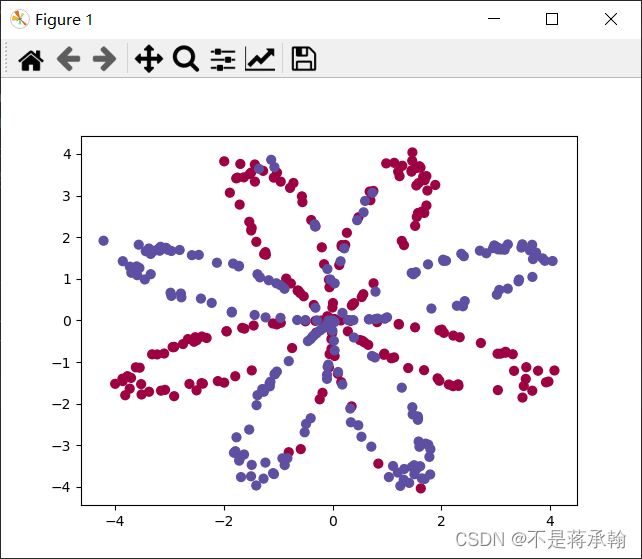
np.random.seed(1)
m=400 #样本数量
N=int(m/2)#每一类的点的个数
D=2 #维度
x=np.zeros((m,D))
y=np.zeros((m,1),dtype='uint8')#label向量，0表示红色，1表示蓝色
a=4
for j in range(2):
    ix=range(N*j,N*(j+1))
    t=np.linspace(j*3.12,(j+1)*3.12,N)+np.random.randn(N)*0.2  #角度
    r=a*np.sin(4*t)+np.random.randn(N)*0.2 #半径
    x[ix]=np.c_[r*np.sin(t),r*np.cos(t)]
    y[ix]=j

plt.scatter(x[:,0],x[:,1],c=y.reshape(-1),s=40,cmap=plt.cm.Spectral)
plt.show()

 

我们可以先尝试用logistic回归来解决这个问题

x=torch.from_numpy(x).float()
y=torch.from_numpy(y).float()
w=nn.Parameter(torch.randn(2,1))
b=nn.Parameter(torch.zeros(1))
 
optimizer=torch.optim.SGD([w,b],1e-1)
 
def logistic_regression(x):
    return torch.mm(x,w)+b
 
criterion=nn.BCEWithLogitsLoss()
for e in range(100):
    out = logistic_regression(Variable(x))
    loss = criterion(out,Variable(y))
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    if(e+1)%20==0:
        print('epoch:{},loss:{}'.format(e+1,loss.item()))

epoch:20,loss:0.6770725846290588
epoch:40,loss:0.6732333302497864
epoch:60,loss:0.6731482148170471
epoch:80,loss:0.6731463074684143
epoch:100,loss:0.6731461882591248

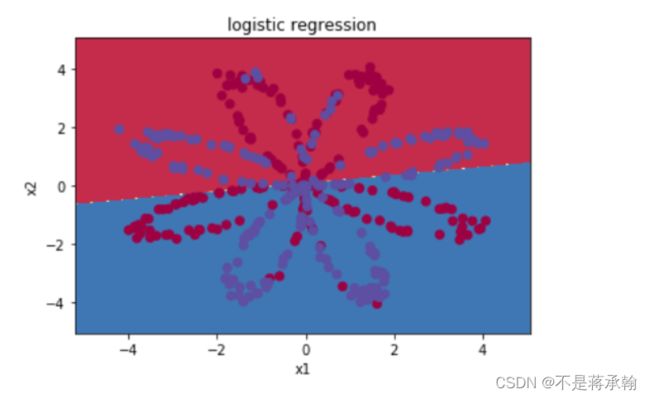
def plot_logistic(x):
    x=Variable(torch.from_numpy(x).float())
    out=torch.sigmoid(logistic_regression(x))
    out =(out>0.5)*1
    return out.data.numpy()

 可以看到，逻辑回归并不能很好的区分开这个复杂的数据集，如果你还记得前面的内容，你就知道逻辑回归是一个线性分类器，这个时候就该我们的神经网络登场了

#定义两层神经网络的参数
w1=nn.Parameter(torch.randn(2,4)*0.01) #隐藏层神经元个数2
b1=nn.Parameter(torch.zeros(4))
 
w2=nn.Parameter(torch.randn(4,1)*0.01)
b2=nn.Parameter(torch.zeros(1))
 
#定义模型
def two_network(x):
    x1=torch.mm(x,w1)+b1
    x1=torch.tanh(x1)
    x2=torch.mm(x1,w2)+b2
    return x2
 
optimizer = torch.optim.SGD([w1,w2,b1,b2],1.)#SGD 随机梯度下降。为了使用torch.optim,需要构建optimizer对象，这个对象能够保持当前参数状态并基于计算得到的梯度进行参数更新
criterion = nn.BCEWithLogitsLoss()
#我们训练10000次
for e in range(10000):
    out =two_network(Variable(x))
    loss = criterion(out,Variable(y))
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    if (e+1)%1000==0:
        print('epoch:{},loss:{}'.format(e+1,loss.item()))

epoch:1000,loss:0.28508755564689636
epoch:2000,loss:0.2724120020866394
epoch:3000,loss:0.2652736008167267
epoch:4000,loss:0.2597547769546509
epoch:5000,loss:0.23341608047485352
epoch:6000,loss:0.22552873194217682
epoch:7000,loss:0.22191940248012543
epoch:8000,loss:0.21951544284820557
epoch:9000,loss:0.21767665445804596
epoch:10000,loss:0.21617057919502258

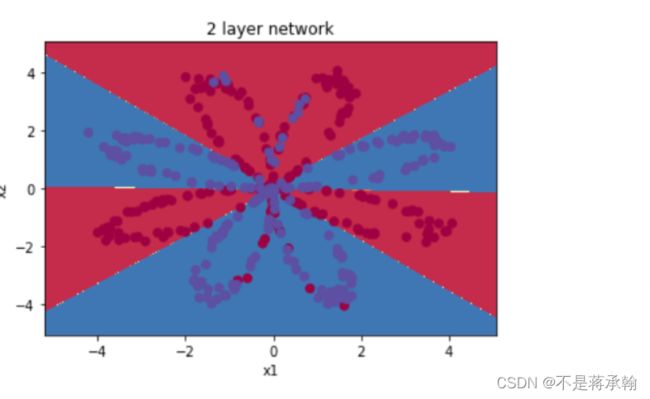
def plot_network(x):
    x=Variable(torch.from_numpy(x).float())
    x1=torch.mm(x,w1)+b1
    x1=torch.tanh(x1)
    x2=torch.mm(x1,w2)+b2
    out=torch.sigmoid(x2)
    out=(out>0.5)*1
    return out.data.numpy()

可以看到神经网络能够非常好的分类这个复杂的数据，和前面的逻辑回归相比，神经网络因为有了激活函数的存在，成了一个非线性分类模型，所以神经网络的分类更复杂

心得体会：

        本次实验很好的回顾了之前学习的反向传播，并与之前的简单的梯度下降做了对比，用白话说，梯度下降就是计算出预测结果与真实结果的误差，然后计算当时参数下误差的梯度是什么，然后沿着梯度，把误差“下降”下来，这就是梯度下降。

 y是真实值， 是预测函数计算出来的预测值，线性回归使用的是平方误差，然后根据误差，计算梯度，再对参数进行调整，这就是梯度下降。

        这里可以看到，对于这个没有隐层的神经网络，对于输出层的参数可以直接计算出误差然后进行梯度下降，因为也没有其他层了。可是如果对于一个多层的神经网络，每一层都有参数，因此如果想要使用梯度下降，要对每一层分别求梯度下降，而梯度下降时误差主导的，也就是说没有误差是无法进行梯度下降的，梯度是和每个样本的x和y有关，也就是输入输出值。可对于神经网络来说，中间的隐层是没有目标值的，那也就没办法计算误差，自然也没办法进行梯度下降，因此就引出了反向传播。

        所以梯度下降只能对于单层使用，多层还得反向传播，梯度下降和反向传播的区别就在于此。现在我对反向传播这个词也有了大概的理解，因为在计算梯度的时候是需要计算出误差后，才能计算出梯度，而中间层没有办法计算出误差，所以需要把输出层的误差反向传播到前面的隐层，这样才能计算梯度。
 

参考链接：

逻辑回归与神经网络还有Softmax regression的关系与区别_weixin_30480075的博客-CSDN博客

PyTorch | 激活函数（Sigmoid、Tanh、ReLU和Leaky ReLU）_软耳朵DONG的博客-CSDN博客_pytorch sigmoid