nndl-book-笔记-基础模型第五章-卷积神经网络
第5 章卷积神经网络
卷积神经网络(Convolutional Neural Network,CNN或ConvNet)是一种具有局部连接、权重共享等特性的深层前馈神经网络。
1)最早是主要用来处理图像信息。使用全连接处理图像有两个缺点,:参数过多;局部不变特性(所以出现卷积操作)。
2)卷积神经网络一般是由卷积层、汇聚层和全连接层交叉堆叠而成的前馈神经网络,使用反向传播算法进行训练(更新参数。
3)CNN特性:局部连接;权值共享(一组连接共享一个参数);汇聚。
4)CNN应用:图像和视频分析的各种任务上,比如图像分类、人脸识别、物体识别、图像分割等,近年来应用到自然语言处理、推荐系统等领域。
5.1 卷积
1)一维卷积:一维卷积经常用在信号处理中,用于计算信号的延迟累积。
2)二维卷积:卷积与互相关操作类似,只是卷积 操作要先将卷积核翻转180°,后进行乘积求和。其中,卷积核选取的不同,会导致卷积操作后的结果不同,效果不同。一幅图像在经过卷积操作后得到结果称为特征映射。
5.1.1 互相关
1)在具体实现时,一般会以互相关操作来代替卷积,从而会减少一些不必要的操作或开销(卷积核翻转)。
2)很多深度学习工具中卷积操作其实都是互相关操作。 可以表述为: Y = W ⊗ X
5.1.2 卷积的变种
1)在卷积的基础上,引入滤波器的滑动步长和零填充来增加卷积的多样性,可以更灵活地进行特征抽取。
1)假设卷积层的输入神经元个数为n,卷积大小为m,步长(stride)为s,输入神经元两端各填补p 个零(zero padding),那么该卷积层的神经元数量为(n − m + 2p)/s + 1。
其中n+2p为填充后的总长度,减去m为移动的总长度,/s为移动多少次,+1为之间-2p的补充。
故通常取合适值,使得(n+2p-m)/s+1 为整数
2)常用的三种卷积,而卷积一般默认为等宽卷积。
5.1.3 卷积的数学性质
1)在宽卷积的情况下,即p=m-1时,具有交换性,x⊗y = y⊗x。
1)卷积中的导数结论(推导有些迷...):假设Y = W⊗X,其中X ∈ RM×N,W ∈ Rm×n,Y ∈ R(M−m+1)×(N−n+1
1、f(Y ) 关于W 的偏导数为X 和∂f(Y )/∂Y的卷积,![]()
2、f(Y ) 关于X 的偏导数为W 和∂f(Y )/∂Y的宽卷积。
5.2 卷积神经网络
卷积神经网络一般由卷积层、汇聚层和全连接层构成。
5.2.1 用卷积来代替全连接
1)由于全连接层导致的参数过多,所以想到使用卷积层替代全连接层。
用卷积来代替全连接,第l 层的净输入z(l) 为第l −1 层活性值a(l−1)和滤波器w(l) ∈ Rm 的卷积,即
z(l) = w(l) ⊗ a(l−1) + b(l),
其中滤波器w(l) 为可学习的权重向量,b(l) ∈ Rnl−1为可学习的偏置。(目的为了减少参数)
2)卷积操作的特点:局部连接(下一层的神经元与上一层的所有神经元相连);
权值共享(作为参数的滤波器w(l) 对于第l 层的所有的神经元都是相同的。即对不同的神经元权值相同)
5.2.2 卷积层
1)卷积层的作用是提取一个局部区域的特征,不同的卷积核相当于不同的特征提取器。
2)特征映射(Feature Map):为一幅图像(或其它特征映射)在经过卷积提取到的特征,每个特征映射可以作为一类抽取的图像特征。(可以说是图像矩阵经过卷积操作后所产生的结果矩阵么)为了提高卷积网络的表示能力,可在不同层上采用不同的卷积核,以得到不同的特征映射。
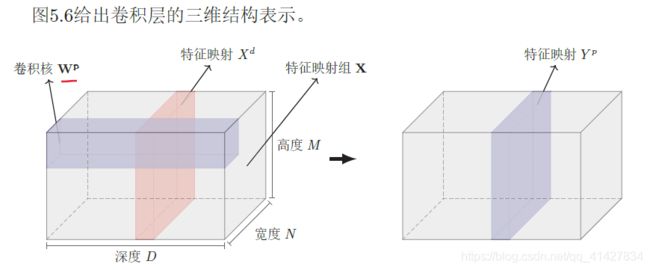
3)下图为3维卷积层表示,其中输入特征映射为输入的图像矩阵,用卷积替换全连接,计算输出特征映射。
5.2.3 汇聚层(pooling layer 池化层)
1)卷积层可以减少网络中连接的数量,但特征映射组中的神经元个数并没有显著减少。之所以不能在卷积层之后直接加分类器,是因为维度过高,容易出现过拟合现象,因此需要有池化层(汇聚层)来降低特征维数,避免过拟合。并从而减少参数数量。
2)汇聚操作:最大汇聚(取出同一区域内,数值最大的值);平均汇聚(使用一个区域内的平均值来代表)
3)典型的汇聚层是将每个特征映射划分为2×2 大小的不重叠区域,然后使用最大汇聚的方式进行下采样。汇聚层也可以看做是一个特殊的卷积层,卷积核大小为m×m,步长为s × s,卷积核为max函数或mean 函数。过大的采样区域会急剧减少神经元的数量,会造成过多的信息损失。
5.2.4 典型的卷积网络结构
1)卷积层-->激活层(激活层目的是在卷积操作之后,加入非线性函数,否则线性函数的叠加无法达到学习参数的效果)
(卷积层-->激活层)-->汇聚层(池化层)(为了减少卷积操作后的特征映射参数,常见2*2的区域内最大汇聚)
上述----->全连接层(是为了完成所需任务,如分类任务中全连接层充当最终划分结果的操作)
最后的softmax 应该是归一化操作,完成映射。
2)网络结构趋向于使用更小的卷积核(比如1 × 1 和3 × 3)以及更深的结构(比如层数大于50)。由于卷积的操作性越来越灵活(比如不同的步长),汇聚层的作用变得也越来越小,因此目前比较流行的卷积网络中,汇聚层的比例也逐渐降低,趋向于全卷积网络。(卷积核为奇数是为了实现等宽卷积,深度越深是为了能够学习到更高层次的特征)
5.3 参数学习(看书推导....)
5.4 几种典型的卷积神经网络
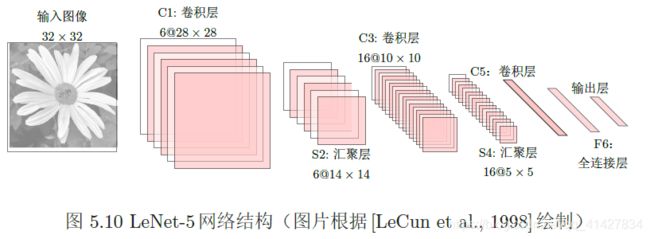
5.4.1 LeNet-5:手写体数字识别
https://blog.csdn.net/saw009/article/details/80590245将的很清楚
5.4.2 AlexNet
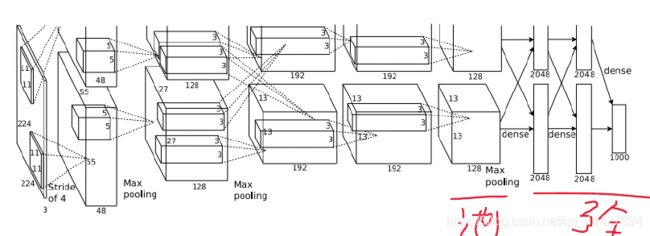
1)是第一个现代深度卷积网络模型,使用GPU进行并行训练,采用了ReLU 作为非线性激活函数,使用Dropout 防止过拟合,使用数据增强来提高模型准确率等。
2)AlexNet结构:包括5个卷积层、3个全连接层和1个softmax层。
关于结构讲解: https://blog.csdn.net/forsch/article/details/84893277
5.4.3 Inception 网络(如论文中,不赘述)
5.4.4 ResNet 网络(同上)
5.5 其它卷积方式
旨在通过步长和零填充进行不同的卷积操作。
5.5.1 转置卷积
1)为了实现从低维度到高纬度的映射,此过程称为转置卷积。
5.5.2 空洞卷积 (为了增加输出结果的感受野)
对于一个卷积层,如果希望增加输出单元的感受野,一般可以通过三种方式实现:(1)增加卷积核的大小;(2)增加层数;(3)在卷积之前进行汇聚操作。前两种操作会增加参数数量,而第三种会丢失一些信息。
1)空洞卷积是一种不增加参数数量,同时增加输出单元感受野的一种方法。
2)空洞卷积通过给卷积核插入“空洞”来变相地增加其大小。如果在卷积核的每两个元素之间插入d − 1 个空洞,卷积核的有效大小为:
m′ = m + (m − 1) × (d − 1) 空洞卷积的动图见: https://nndl.github.io/v/cnn-conv-more
其中d 称为膨胀率(Dilation Rate)。当d = 1 时卷积核为普通的卷积核。