PyTorch——深度学习多分类问题

多分类问题的要点

一、本文使用手写数字识别来讲解多分类问题，首先了解一下一些开源常用数据集的调用

• torchvision.datasets——通过from torchvision import datasets来调用
  1. 这个包中有MNIST, Fashion-MNIST, EMNIST, COCO, LSUN, ImageFolder, DatasetFolder, Imagenet-12, CIFAR, STL10, PhotoTour等常用数据集，同时提供了一些重要的参数设置来实现调用
  2. 上述的datasets都是torch.utils.data.Dataset的子类，即都继承了Dataset。所以它们都具有__getitem__和__len__两个方法，并且都可以传递给torch.utils.data.Dataset来使用多线程。
     例如官网的例子：

     imagenet_data = torchvision.datasets.ImageNet('path/to/imagenet_root/')
     data_loader = torch.utils.data.DataLoader(imagenet_data,
                                       batch_size=4,
                                       shuffle=True,
                                       num_workers=args.nThreads)
     

• MNIST的参数介绍：

  torchvision.datasets.MNIST（root, train=True, transform = None, target_transform = None, download = False）
  # root：数据集的根目录，包括training.pth和test.pt
  # train：True表示训练集，False表示测试集
  # download：True表示从互联网下载数据集，并把数据集放在root目录下，如果下载过，就不再下载
  # transform：函数/转换，将接受到的数据集转换为设置的类型，例如transforms.ToTensor
  # target_transform：对目标进行转换
  

二、 关于Softmax Classifier的理解

• 关于多分类问题，就是将每个标签都看成二分类的问题，输出它属于每一类的概率值，同时又要满足离散分布的要求，即属于每一类的概率之和为1 $(P_1+\dots +P_N=1)$。
• Softmax函数
  $$P(Y=i)=\frac{e^{z_i}}{{\sum }_{j=0}^{K-1}{e}^{z_j}},i\in \{0,\dots ,K-1\}$$
  其中，$z_l\in {\mathbb{R}}^K$表示第$l$层的线性输出，即求出线性输出的指数并除以指数总和sum。该函数可以保证概率值都大于0，并且属于每个分类的概率值总和为1。

三、多分类的损失函数

• 分类问题使用交叉熵损失函数，首先回顾一下二分类的交叉熵损失函数：
  $$BCE=-\sum _{x_i}{P}_{D_1}(x)\cdot ln{P}_{D_2}(x)=-\left[ylog\hat{y}+(1-y)log(1-\hat{y})\right]$$
  1. 在二分类问题中y=0/1。同样在多分类问题中，y的取值也是0或者1，此处数字代表是否属于该类别，例如手写数字0-9识别中，如果y=torch.LongTensor([9])，则对应标签应该是[0,0,0,0,0,0,0,0,0,1]。
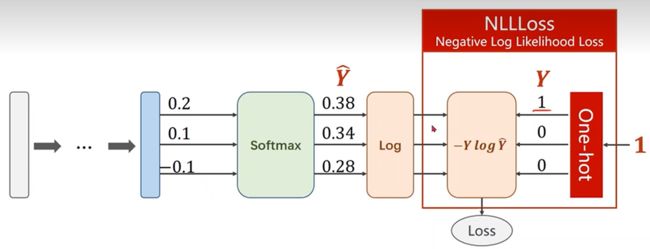
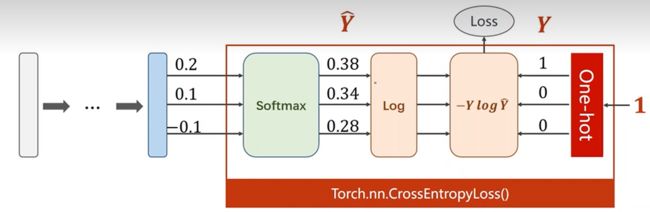
  2. 所以损失函数$loss(\hat{Y},Y)=-Ylog\hat{Y}$，如下图所示pytorch提供的torch.nn.CrossEntryLoss()实际上是LogSoftmax和NLLLoss的结合。

代码详解与运行结果

一、导入库

import torch
from torch.utils.data import DataLoader #创建可以迭代的数据装载器
from torchvision import datasets  #调用数据集
from torchvision import transforms  #图像预处理包 

import torch.nn.functional as F  #调用激活函数ReLU
import torch.optim as optim #使用优化器
import matplotlib.pyplot as plt

二、Prepare Dataset

batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307, ), (0.3081, ))])
#ToTensor可以将灰度范围从0~255变换到0~1之间，normalize是用均值和标准差归一化张量图像

#训练集
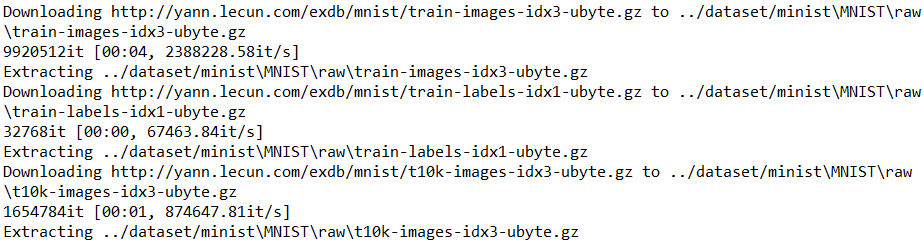
train_dataset = datasets.MNIST(root = '../dataset/minist', train = True, download = True, transform = transform)
train_loader = DataLoader(train_dataset, shuffle = True, batch_size = batch_size)
#测试集
test_dataset = datasets.MNIST(root = '../dataset/minist', train = False, download = True, transform = transform)
test_loader = DataLoader(test_dataset, shuffle = False, batch_size = batch_size)

• transforms.Compose([ , , ])：把多个步骤整合在一起
• transforms.ToTensor()图解：
  
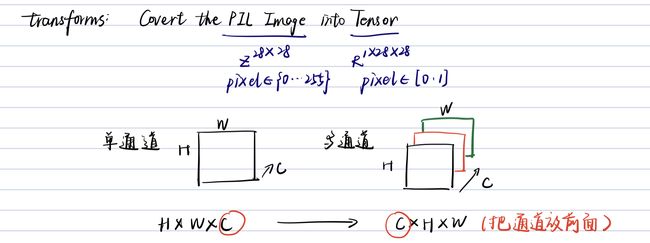
• transforms.Normalize((mean, ), (std, ))：归一化$image=（image-mean）/std$

三、Design Model and Using Class

class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        #定义五层神经网络
        self.l1 = torch.nn.Linear(784, 512)
        self.l2 = torch.nn.Linear(512, 256)
        self.l3 = torch.nn.Linear(256, 128)
        self.l4 = torch.nn.Linear(128, 64)
        self.l5 = torch.nn.Linear(64, 10)
        
    def forward(self, x):
        x = x.view(-1, 784)  #重新排成一个矩阵,-1是自动获取矩阵的维数
        x = F.relu(self.l1(x))  #使用relu激活函数
        x = F.relu(self.l2(x))
        x = F.relu(self.l3(x))
        x = F.relu(self.l4(x))
        return self.l5(x) #最后一层不使用激活函数，直接传入softmax
      
#实例化
model = Net()

四、Construct Loss and Optimizer

criterion = torch.nn.CrossEntropyLoss() #使用交叉熵函数
optimizer = optim.SGD(model.parameters(), lr = 0.01, momentum = 0.5) #momentum:使用带冲量的模型来优化训练过程

五、Train and Test

#把训练过程封装成一个函数
def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        #记录下了迭代次数以及训练数据
        inputs, target = data
        optimizer.zero_grad() #优化器使用之前先清零
     
        #forward + backward + update
        outputs = model(inputs)
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()
        
        running_loss += loss.item()
        if batch_idx % 300 == 299: #三百个为一个小批量，每三百次输出一次，减少计算成本
            print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
            running_loss = 0.0 #损失清零
    return loss.item()        
#把测试过程也封装起来，不需要计算反向传播，只需要正向的
def test():
    correct = 0
    total = 0
    with torch.no_grad(): #全程不计算梯度
        for data in test_loader:
            images, labels = data #记录原始值
            outputs = model(images) #把图像丢进模型训练，得到输出结果
            _, predicted = torch.max(outputs.data, dim = 1)  #求每一行最大值的下标
            #输出的outputs是N *1的，dim=1指的是沿着第1个维度，-->，即列，行是第0个维度
            #返回两个值，最大值下标以及最大值是多少
            total += labels.size(0) #记录有多少条labels
            correct += (predicted == labels).sum().item() #相同的求和取标量
    print('Accuracy on test set: %d %% ' % (100 * correct / total))
    return correct / total

六、主函数

if __name__ == '__main__':
	loss_list = []
	acc_list = []
	epoch_list = []
	
    for epoch in range(10):
        loss = train(epoch)  #训练一次
        accuracy = test() #测试一次
        
        loss_list.append(loss)
        acc_list.append(accuracy)
        epoch_list.append(epoch)
    #绘图
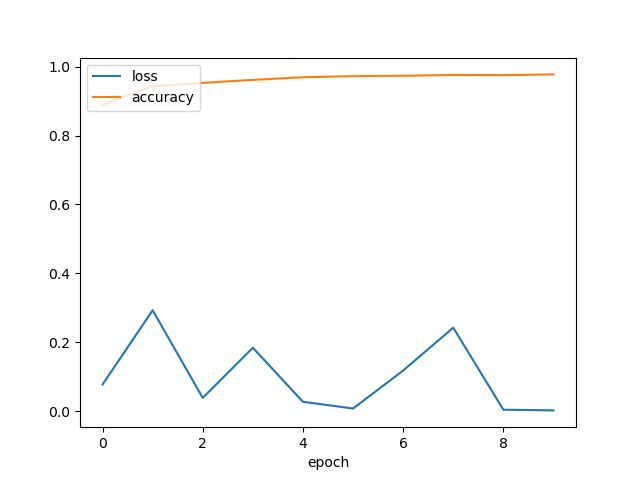
    plt.plot(epoch_list, loss_list)
    plt.plot(epoch_list, acc_list)
    plt.xlabel('epoch')
    plt.show()

七、运行结果

Processing...
Done!
[1,   300] loss: 2.262
[1,   600] loss: 1.163
[1,   900] loss: 0.447
Accuracy on test set: 89 % 
[2,   300] loss: 0.324
[2,   600] loss: 0.272
[2,   900] loss: 0.232
Accuracy on test set: 94 % 
[3,   300] loss: 0.185
[3,   600] loss: 0.173
[3,   900] loss: 0.157
Accuracy on test set: 95 % 
[4,   300] loss: 0.135
[4,   600] loss: 0.118
[4,   900] loss: 0.121
Accuracy on test set: 96 % 
[5,   300] loss: 0.097
[5,   600] loss: 0.101
[5,   900] loss: 0.094
Accuracy on test set: 96 % 
[6,   300] loss: 0.077
[6,   600] loss: 0.077
[6,   900] loss: 0.079
Accuracy on test set: 97 % 
[7,   300] loss: 0.061
[7,   600] loss: 0.065
[7,   900] loss: 0.063
Accuracy on test set: 97 % 
[8,   300] loss: 0.051
[8,   600] loss: 0.052
[8,   900] loss: 0.053
Accuracy on test set: 97 % 
[9,   300] loss: 0.036
[9,   600] loss: 0.044
[9,   900] loss: 0.046
Accuracy on test set: 97 % 
[10,   300] loss: 0.033
[10,   600] loss: 0.037
[10,   900] loss: 0.034
Accuracy on test set: 97 % 

1. 可以看出loss在逐步下降，准确率逐渐上升，但是损失和测试集的准确率会达到一个极限，因为例如本文使用的是全连接的神经网络，图像中的一些局部信息会被忽略。
2. 并且在训练图像时会更关心高抽象级别的特征，所以特征提取后再分类训练效果会更好（常见：Auto-CNN自动提取图像特征、FFT傅里叶变换、Wawelet小波）。