matlab求解常微分方程——从原理到实践（代码详解）

目录

理论知识

一、概念

二、解法

matlab微分方程求解

一、解析解

1.1 解析解的存在

1.2 解析解的解法

1.3 实例

二、数值解

2.1 概述

2.2 优化措施

2.3 解法

2.4 检验

---

理论知识

一、概念

微分方程：含导数或微分的方程。

解：满足微分方程的函数。

特解/通解：特解指的是满足微分方程的某一个解；通解指的是满足微分方程的一组解。

阶：微分方程中导数或微分的最高阶数。

线性/非线性：（几何意义：叠加原理）方程中的函数和它的各阶导数都是一次方为线性微分方程，否则为非线性。例：

• y'=sin(x)*y 线性
• y'=y^2 非线性

齐次/非齐次：（代数意义：次数）齐次微分方程中不含常数项,也不含仅由x的各种运算组合构成的项（比如4xx,sinx等），否则为非齐次。

常微分/偏微分：未知函数是一元函数的，叫常微分方程；未知函数是多元函数的叫做偏微分方程。

初值问题和边值问题：附加条件中未知函数及其导数的独立变量取值相同，则为初值问题；附加条件中未知函数及其导数的独立变量取值不同，则为边界值问题。例：

• y(0)=1,y'(0)=2 初值问题
• y(0)=1,y'(1)=2 边值问题

二、解法

在matlab中解微分方程，方法有两种：

解析解方法：严格按照公式逻辑推导得到的，具有基本的函数形式。

数值解方法：采用某种计算方法，在特定的条件下得到的一个近似数值结果，如有限元法，数值逼近法，插值法等等。

解析解方法可回顾《高等数学》中相关公式。

数值解方法可回顾《数值分析》中相关解法。

matlab微分方程求解

一、解析解

1.1 解析解的存在

由Abel-Ruffini定理，四次及以下的多项式代数方程是能求出根的解析解的，即低阶常系数线性微分方程有一般意义下的解析解。

非线性微分方程只能用数值解法求解，即使看起来很简单的非线性微分方程也是没有解析解的，只有极特殊的非线性微分方程解析可解。

1.2 解析解的解法

利用dsolve函数

• S = dsolve(eqn)
• S = dsolve(eqn,cond)
• S = dsolve(___,Name,Value)
• [y1,...,yN] = dsolve(___)

1.3 实例

例1.1 输入信号为u(t)=exp(-5*t)*cos(2*t+1)+5，求微分方程diff(y,4)+10*diff(y,3)+35*diff(y,2)+50*diff(y)+24*y=5*diff(u,t,2)+4*diff(u,t)+2*u的通解。初值条件：y(0)=3,y1(0)=2,y2(0)=0,y3(0)=0，求方程的特解。（约定y1代表一阶导数，以此类推）

代码如下：

% y=dsolve(f1,f2,...,fm) 默认自变量为t
% y=dsolve(f1,f2,...,fm,'x') 指明自变量
% f可由字符串表示也可由符号表达式表示

%用字符串表达式，新版本会被移除
syms t; 
u=exp(-5*t)*cos(2*t+1)+5;
uu=5*diff(u,t,2)+4*diff(u,t)+2*u;
y=dsolve(['D4y+10*D3y+35*D2y+50*Dy+24*y=',char(uu)]); %求解
y=simplify(y) %化简

%用符号表达式，推荐
syms y(t); 
eqn=diff(y,4)+10*diff(y,3)+35*diff(y,2)+50*diff(y)+24*y==uu;
y=dsolve(eqn);
y=simplify(y) 

%检验
diff(y,4)+10*diff(y,3)+35*diff(y,2)+50*diff(y)+24*y-uu

%求特解并绘图
syms y(t); 
eqn=diff(y,4)+10*diff(y,3)+35*diff(y,2)+50*diff(y)+24*y==uu;
y1=diff(y);y2=diff(y,2);y3=diff(y,3);y4=diff(y,4); 
% 需要引入中间变量
% 用字符串求解的情况，不需要引入中间变量。'y(0)=3','Dy(0)=2','D2y(0)=0'...
cond=[y(0)==3,y1(0)==2,y2(0)==0,y3(0)==0];
z=dsolve(eqn,cond);
z=simplify(z)
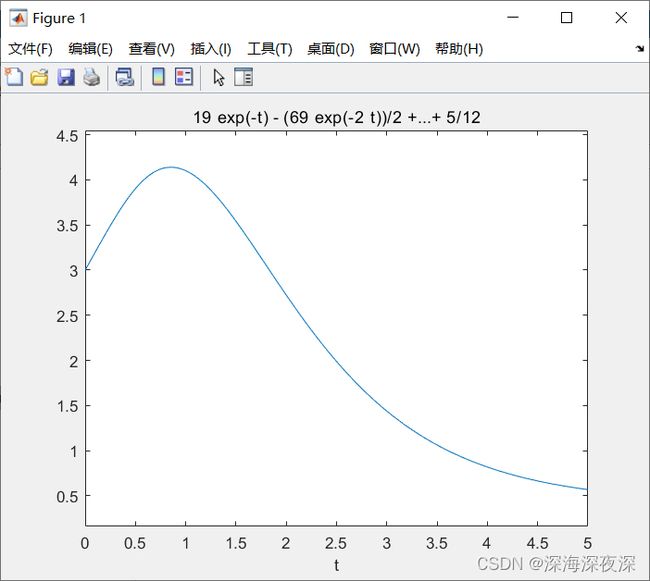
ezplot(z,[0,5])
fplot(z,[0,5])
% ezplot(fun,[xmin,xmax])绘制fun(x)在以下域上的图形:xmin

运行结果：

y =
C1*exp(-4*t) - (547*exp(-5*t)*sin(2*t + 1))/520 - (343*exp(-5*t)*cos(2*t + 1))/520 + C2*exp(-3*t) + C3*exp(-2*t) + C4*exp(-t) + 5/12

ans =0

z =
19*exp(-t) - (69*exp(-2*t))/2 + (73*exp(-3*t))/3 - (25*exp(-4*t))/4 + (97*exp(-t)*sin(1))/60 - (51*exp(-2*t)*sin(1))/13 + (5*exp(-3*t)*sin(1))/8......

ans = 0.5679 

z1 = 
(exp(-5*t)*(445*cos(2*t + 1) - 65*exp(5*t) + 102*sin(2*t + 1)))/26 - (exp(-5*t)*(537*cos(2*t + 1) - 40*exp(5*t) + 15*sin(2*t + 1)))/24 - (exp(-5*t)*(25*exp(5*t) - 542*cos(2*t + 1) ......

例1.2 求解有复数极点的微分方程diff(y,5)+5*diff(y,4)+12*diff(y,3)+16*diff(y,2)+12*diff(y)+4*y=diff(u)+3*u，输入信号：u(t)=sin(t)，初值条件：y(0)=0,y1(0)=0,y2(0)=0,y3(0)=0,y4(0)=0

代码如下：

% 有复数极点的微分方程
syms y(t) u(t); 
u=sin(t);
uu=diff(u)+3*u;
eqn=diff(y,5)+5*diff(y,4)+12*diff(y,3)+16*diff(y,2)+12*diff(y)+4*y==uu;
y1=diff(y);y2=diff(y,2);y3=diff(y,3);y4=diff(y,4); % 需要引入中间变量
cond=[y(0)==0,y1(0)==0,y2(0)==0,y3(0)==0,y4(0)==0];
y=dsolve(eqn,cond);
y=simplify(y)
fplot(y,[0,30])
% 检验
diff(y,5)+5*diff(y,4)+12*diff(y,3)+16*diff(y,2)+12*diff(y)+4*y-uu

 运行结果：

y =
exp(-t) - cos(t)/5 - (2*sin(t))/5 - (4*exp(-t)*cos(t))/5 + (11*exp(-t)*sin(t))/10 - (t*exp(-t)*cos(t))/2

ans =0

 例1.3 求线性微分方程组

• diff(y)==4*x+3*y+4*exp(-t))
• diff(x,2)+2*diff(x)==x+2*y-exp(-t)

代码如下：

%微分方程组,无法检验结果
syms y(t) x(t);
eqn1=diff(x,2)+2*diff(x)==x+2*y-exp(-t);
eqn2=diff(y)==4*x+3*y+4*exp(-t);
[x,y]=dsolve(eqn1,eqn2)
diff(x,2)+2*diff(x)-x+2*y-exp(-t)
diff(y)-4*x+3*y+4*exp(-t)

 运行结果：

x =
exp(t*(6^(1/2) + 1))*(6^(1/2)/5 - 1/5)*(C2 + exp(- 2*t - 6^(1/2)*t)*((11*6^(1/2))/3 - 37/4)) - exp(-t)*(C1 + 6*t) - exp(-t*(6^(1/2) - 1))*(6^(1/2)/5 + 1/5)*(C3 - exp(6^(1/2)*t - 2*t)*((11*6^(1/2))/3 + 37/4))
 
y =
exp(-t)*(C1 + 6*t) + exp(t*(6^(1/2) + 1))*((2*6^(1/2))/5 + 8/5)*(C2 + exp(- 2*t - 6^(1/2)*t)*((11*6^(1/2))/3 - 37/4)) - exp(-t*(6^(1/2) - 1))*((2*6^(1/2))/5 - 8/5)*(C3 - exp(6^(1/2)*t - 2*t)*((11*6^(1/2))/3 + 37/4))
 
ans =(无法检验)
4*exp(-t)*(C1 + 6*t) - exp(-t) - exp(t*(6^(1/2) + 1))*(6^(1/2)/5 - 1/5)*(C2 + exp(- 2*t - 6^(1/2)*t)*((11*6^(1/2))/3 - 37/4)) + ......
 
ans =(无法检验)
10*exp(-t) + 6*exp(-t)*(C1 + 6*t) - 4*exp(t*(6^(1/2) + 1))*(6^(1/2)/5 - 1/5)*(C2 + exp(- 2*t - 6^(1/2)*t)*((11*6^(1/2))/3 - 37/4)) +......

 例1.4 求解自变量为x的时变线性微分方程(2*x+3)^3*diff(y,3)+3*(2*x+3)*diff(y)-6*y=0

代码如下：

% 自变量为x的时变微分方程
syms x y(x);
y=dsolve((2*x+3)^3*diff(y,3)+3*(2*x+3)*diff(y)-6*y==0)；
simplify(y)
(2*x+3)^3*diff(y,3)+3*(2*x+3)*diff(y)-6*y

运行结果：

y =
C1*(x + 3/2) - 2*C2*(x + 3/2)^(1/2) + C3*(2*x + 6)*(x + 3/2)^(1/2)

ans =(无法检验)
12*C2*(x + 3/2)^(1/2) - 6*C1*(x + 3/2) - (2*x + 3)^3*((3*C3)/(2*(x + 3/2)^(3/2)) + (3*C2)/(4*(x + 3/2)^(5/2)) - (3*C3*(2*x + 6))/(8*(x + 3/2)^(5/2))) + (6*x + 9)*(C1 - C2/(x + 3/2)^(1/2) + 2*C3*(x + 3/2)^(1/2) + (C3*(2*x + 6))/(2*(x + 3/2)^(1/2))) - 6*C3*(2*x + 6)*(x + 3/2)^(1/2)
 

例1.5 求解高阶常系数微分方程组

• diff(x,2)-x+y+z=0
• x+diff(y,2)-y+z=0
• +y+diff(z,2)-z=0

 代码如下：

% 高阶常系数线性微分方程
syms x(t) y(t) z(t);
eqn1=diff(x,2)-x+y+z==0;
eqn2=x+diff(y,2)-y+z==0;
eqn3=x+y+diff(z,2)-z==0;
x1=diff(x);y1=diff(y);z1=diff(z);
cond=[x(0)==1,y(0)==0,z(0)==0,x1(0)==0,y1(0)==0,z1(0)==0];
[x y z]=dsolve(eqn1,eqn2,eqn3,cond)
% 检验，成功
diff(x,2)-x+y+z
x+diff(y,2)-y+z
x+y+diff(z,2)-z

运行结果：

x =
exp(2^(1/2)*t)/3 + exp(-2^(1/2)*t)/3 + cos(t)/3
 
y =
cos(t)/3 - exp(-2^(1/2)*t)/6 - exp(2^(1/2)*t)/6
 
z =
cos(t)/3 - exp(-2^(1/2)*t)/6 - exp(2^(1/2)*t)/6
 
ans =0 

ans =0 

ans =0

例1.6 求解时变线性微分方程x^2*(2*x-1)*diff(y,x,3)+(4*x-3)*x*diff(y,x,2)-2*x*diff(y,x)+2*y=0

代码如下：

% 自变量为x的时变微分方程
syms x y(x);
eqn=x^2*(2*x-1)*diff(y,x,3)+(4*x-3)*x*diff(y,x,2)-2*x*diff(y,x)+2*y==0;
y=dsolve(eqn)；
simplify(y)
% 检验，失败
x^2*(2*x-1)*diff(y,3)-(4*x-3)*x*diff(y,2)-2*x*diff(y)+2*y

运行结果：

y =
-(2*C1 - C3 + 8*C3*x + 32*C2*x^2 + 8*C3*x^2*log(x))/(16*x)

ans =(无法检验)
2*x*((8*C3 + 64*C2*x + 8*C3*x + 16*C3*x*log(x))/(16*x) - (2*C1 - C3 + 8*C3*x + 32*C2*x^2 + 8*C3*x^2*log(x))/(16*x^2))+...
 

例1.7 求解特殊非线性微分方程diff(x)=x*(1-x^2)

代码如下：

% 特殊非线性方程
syms x(t);
x=dsolve(diff(x)==x*(1-x^2))

运行结果：

x =
 (-1/(exp(C1 - 2*t) - 1))^(1/2)
                              0
                              1
                             -1

注：若改为x=dsolve(diff(x)==x*(1-x^2)+1)，则无解。

二、数值解

2.1 概述

大部分为关于微分方程的初值问题的数值解法，这类问题需要用一阶显式微分方程组描述为

x ' ( t ) = f ( t , x ( t ) )

• x(t)=[x1(t);x2(t);...xn(t)] 状态向量
• f(.)=[f1(.);f2(.);...fn(.)] 任意非线性函数
• x0=[x1(t0);x2(t0);...xn(t0)] 初始状态
• [t0,tn] 时间区间（tn为终止时间） 

2.2 优化措施

• 选择适当的步长h：不能太大和太小，太大精度不够，太小减慢计算精度，增加计算次数从而增加累积误差。
• 改进近似算法精度：Euler算法将原始积分进行梯形近似，精度低；精度较高的是Runge-Kutta法和Adams法。
• 采用变步长方法：采用自适应步长算法。

2.3 解法

1、手动编写算法。例如：

四阶定步长Runge-Kutta算法matlab代码如下：

function [tout,yout]=rk_4(fun,tspan,y0)
ts=tspan;
t0=ts(1);
tf=ts(2);
yout=[];
tout=[];
y0=y0(:);
if length(tspan)==3,
   h=ts(3);
else, 
   h=(ts(2)-ts(1))/100;
   tf=ts(2); 
end
for t = [t0:h:tf] % 对各个时间点循环计算
    k1=h*fun(t,y0);
    k2=h*fun(t+h/2,y0+k1/2);
    k3=h*fun(t+h/2,y0+k2/2);
    k4=h*fun(t+h,y0+k3);
    y0=y0+(k1+2*k2+2*k3+k4)/6;
    yout=[yout;y0.'];
    tout=[tout;t];
end

2、ode系列函数：最常用ode45()

介绍

ode45()实现了变步长四阶五级 Runge-Kutta-Felhberg算法，可以使用变步长的方法求解微分方程。ode系列函数功能总结如下：

用法

函数调用：

• [t,y] = ode45(odefun,tspan,y0)
• [t,y] = ode45(odefun,tspan,y0,options)
• [t,y,te,ye,ie] = ode45(odefun,tspan,y0,options)
• sol = ode45(___)

微分方程/组描述：

• function xd=funname(t,x) % 不需要附加参数格式
• function xd=funname(t,x,p1,p2,...,pm) % 可以使用附加参数

控制条件：使用odesrt()函数创建或修改 options 结构体。

• options=odeset('RelTol',1e-7)
• options=odeset;options.RelTol=1e-7

例：options = odeset('RelTol',1e-5,'Stats','on','OutputFcn',@odeplot) 指定 1e-5 的相对误差容限、打开求解器统计信息的显示，并指定输出函数 @odeplot 在计算时绘制解。

实例

例2.1 解微分方程组

• diff(x1)=-beta*x1+x2*x3
• diff(x2)=-Pho*x2+Pho*x3
• diff(x3)=-x1*x2+sigma*x2-x3

 其中，beta=8/3,Pho=10,sigma=28，初值:x1(0)=x2(0)=0,x3(0)=10e-10

代码1：（不带有附加参数的函数）

f=@(t,x) [-8/3*x(1)+x(2)*x(3);-10*x(2)+10*x(3);-x(1)*x(2)+28*x(2)-x(3)]
% 编写匿名函数描述动态模型
tn=100;
x0=[0;0;1e-10];
[t,x]=ode45(f,[0,tn],x0); %求方程数值解
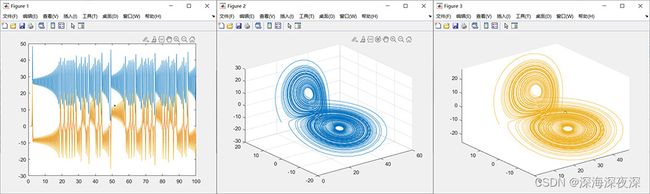
plot(t,x);
figure;
plot3(x(:,1),x(:,2),x(:,3)); %相空间轨迹三维图
grid % 显示或隐藏坐标区网格线
figure;
comet3(x(:,1),x(:,2),x(:,3)); %绘制动画式轨迹

运行结果：

代码2：（带有附加参数的函数）

函数程序：

function f=c_7_2_fun
% 定义一个接口，通过匿名函数调用
% 通过定义接口的方式，在一个函数文件实例里可编写多个函数
f.lorenz1=@lorenz1;
end

function dx=lorenz1(t,x,b,r,s) % 带有附加参数的微分方程描述曲线
dx=[-b*x(1)+x(2)*x(3);-r*x(2)+r*x(3);-x(1)*x(2)+s*x(2)-x(3)];
end

主程序：

%% 编写带有附加参数的函数
% 函数需列在单独的文件里，且函数名和文件名一致，可通过定义接口的方式，在一个函数文件例里编写多个函数
f=c_7_2_fun % 调用接口
% 设置附加参数的值
b1=8/3;r1=10;s1=28;tn=100;x0=[0;0;1e-10];
[t,x]=ode45(@f.lorenz1,[0,tn],x0,[],b1,r1,s1); % 无需使用和函数一样的变量名
% 求方程数值解
% 空矩阵表示使用默认的控制模版
figure(1);
plot(t,x);
figure(2);
comet3(x(:,1),x(:,2),x(:,3)); %绘制动画式轨迹
grid

%% 改变附加参数的值
b2=2;r2=5;s2=20;tn=100;x0=[0;0;1e-10];
[t2,x2]=ode45(@f.lorenz1,[0,tn],x0,[],b2,r2,s2); 
% 求方程数值解
% 空矩阵表示使用默认的控制模版
figure(3);
plot(t2,x2);
figure(4);
comet3(x2(:,1),x2(:,2),x2(:,3)); %绘制动画式轨迹
grid %只针对上一个绘图

% TIPS
%% 使用匿名函数则可以不用附加参数
b=8/3;r=10;s=28;tn=100;x0=[0;0;1e-10];
f=@(t,x) [-b*x(1)+x(2)*x(3);-r*x(2)+r*x(3);-x(1)*x(2)+s*x(2)-x(3)];
% 匿名函数可以直接使用matlab工作空间中的变量
[t,x]=ode45(f,[0,tn],x0); %求方程数值解
plot(t,x);
figure;
plot3(x(:,1),x(:,2),x(:,3)); %相空间轨迹三维图
grid % 显示或隐藏坐标区网格线

注：函数需列在单独的文件里，且函数名和文件名一致，才可保证正常调用，即一个函数对应一个函数文件；现可通过定义接口的方式，在一个函数文件实例里编写多个函数，调用时调用接口。

运行结果：（改变参数前的运行结果同上）

2.4 检验

• 修改仿真控制参数，例如：将‘RelTol’或'AbsTol'选项设置成一个更小的值，观察结果是否和上次一致，如有不可接受的差异，应考虑进一步减小误差值。
• 选择不同的微分方程求解算法。

本文仅涉及一般常微分方程求解，对于一些特殊常微分方程的求解方法见同专栏相关文章。