原码,补码,反码概念和计算方法详解

原码,补码,反码概念和计算方法详解

一、机器数和真数

1、机器数

一个数在计算机中的二进制表示形式，叫做这个数的机器数。机器数是带符号的，在计算机用一个数的最高位存放符号，正数为0，负数为1.

比如，十进制中的数 +3 ，计算机字长为8位，转换成二进制就是00000011。如果是 -3 ，就是 10000011 。

那么，这里的 00000011 和 10000011 就是机器数。

2、真值

机器数的第一位是符号位，后边才是真正的数值，所以机器数的形式值就不等于真正的数值。例如上面的有符号数10000011，其最高位1代表负，其真正数值是 -3 而不是形式值131（10000011转换成十进制等于131）。所以，为区别起见，将带符号位的机器数对应的真正数值称为机器数的真值。

例：

0000 0001的真值 = +000 0001 = +1

1000 0001的真值 = –000 0001 = –1

二、原码，反码，补码的基础概念和计算方法

在探求为何机器要使用补码之前，让我们先了解原码，反码和补码的概念。对于一个数，计算机要使用一定的编码方式进行存储。 原码，反码，补码是机器存储一个具体数字的编码方式。

1.原码

原码就是符号位加上真值的绝对值，即用第一位表示符号，其余位表示值。比如如果是8位二进制：

[+1]（原码） = 0000 0001

[-1]（原码） = 1000 0001

第一位是符号位。因为第一位是符号位，所以8位二进制数的取值范围就是：

[1111 1111 , 0111 1111]

即

[-127 , 127]

原码是人脑最容易理解和计算的表示方式。

2.反码

反码的表示方法是: 正数的反码是其本身，负数的反码是在其原码的基础上，符号位不变，其余各个位取反。

[+1] = [00000001]（原码）= [00000001]（反码）

[-1] = [10000001]（原码）= [11111110]（反码）

可见如果一个反码表示的是负数，人脑无法直观的看出来它的数值。通常要将其转换成原码再计算。

3.补码

补码的表示方法是：正数的补码就是其本身，负数的补码是在其原码的基础上，符号位不变，其余各位取反，最后+1 (即在反码的基础上+1)。

[+1] = [00000001]（原码） = [00000001]（反码） = [00000001]（补码）

[-1] = [10000001]（原码） = [11111110]（反码） = [11111111]（补码）

对于负数，补码表示方式也是人脑无法直观看出其数值的。通常也需要转换成原码在计算其数值。

三、为何要使用原码，反码和补码

现在我们知道了计算机可以有三种编码方式表示一个数。对于正数因为三种编码方式的结果都相同:

[+1] = [00000001]（原码） = [00000001]（反码） = [00000001]（补码）

所以不需要过多解释. 但是对于负数:

[-1] = [10000001]（原码） = [11111110]（反码） = [11111111]（补码）

可见原码, 反码和补码是完全不同的。既然原码才是被人脑直接识别并用于计算表示方式。为何还会有反码和补码呢?

首先, 因为人脑可以知道第一位是符号位，在计算的时候我们会根据符号位, 选择对真值区域的加减 (真值的概念在本文最开头)。但是对于计算机，加减乘数已经是最基础的运算，要设计的尽量简单。计算机辨别"符号位"显然会让计算机的基础电路设计变得十分复杂! 于是人们想出了将符号位也参与运算的方法。我们知道，根据运算法则减去一个正数等于加上一个负数，即: 1-1 = 1 + (-1) = 0 ，所以机器可以只有加法而没有减法，这样计算机运算的设计就更简单了。

于是人们开始探索，将符号位参与运算，并且只保留加法的方法。首先来看原码：

从上面的原码表中可以看见左边每增加一个二进制单位对应的真数是递减的，而右边每增加一个二进制单位对应的真数是递增的，所以对于原码来说，能满足正数的加法，但无法满足负数的加法

计算十进制的表达式: 1-1=0

1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原 = [10000010]原 = -2

如果用原码表示, 让符号位也参与计算, 显然对于减法来说, 结果是不正确的.这也就是为何计算机内部不使用原码表示一个数。

为了解决原码做减法的问题，出现了反码：

计算十进制的表达式: 1-1=0

1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0

发现用反码计算减法，结果的真值部分是正确的。而唯一的问题其实就出现在"0"这个特殊的数值上。虽然人们理解上+0和-0是一样的，但是0带符号是没有任何意义的。而且会有[0000 0000]原和[1000 0000]原两个编码表示0。

于是补码的出现，解决了0的符号涉及两个编码的问题:

1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [0000 0001]补 + [1111 1111]补 = [0000 0000]补=[0000 0000]原

这样0用[0000 0000]表示, 而以前出现问题的-0则不存在了.而且可以用[1000 0000]表示-128:

(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补

-1-127的结果应该是-128，在用补码运算的结果中，[1000 0000]补 就是-128。但是注意因为实际上是使用以前的-0的补码来表示-128，所以-128并没有原码和反码表示 (对-128的补码表示[1000 0000]补算出来的原码是[0000 0000]原，这是不正确的)。

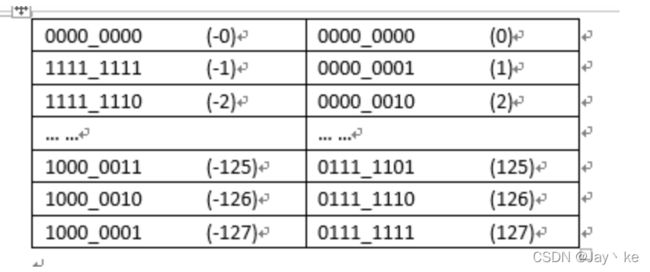
使用补码，不仅仅修复了0的符号以及存在两个编码的问题，而且还能够多表示一个最低数. 这就是为什么8位二进制，使用原码或反码表示的范围为[-127, +127]，而使用补码表示的范围为[-128, 127]

四、Example

设计一个电路实现result[14:0] <= a[7:0] * 8’b1111_1011,用尽量少的资源来实现。写出代码，请完成代码add_result。

• 思路：
  8’b1111_1011 = 9’h100 - 3’b100 - 1’b1
  -a*3’b100 = -({6’h00,a,2’b00}) = ({6’h3f,~a,2’b11}) + 1’b1

module	add_result(
	clk,
	rstn,
	a,
	result
);

	input								clk;
	input								rstn;
	input	[7:0]						a;	
	output  [15:0]				  	 	result;//result <= a * 8'b1111_1011, resutl比a延迟1T
	reg     [15:0]						result;
	
	always@(posedge clk or negedge rstn)
	begin
		if(!rstn)
		begin
			result <= 16'h0000;
		end
		else 
		begin
			result <= {a[7:0],8'h00} + {6'h3F,(~a[7:0]),2'b11} + 1'b1 + {8'hFF,(~a[7:0])} + 1'b1; // result = a* 9'h1_0000_0000 - a*3'b100 -a;
		end
	end
	
endmodule