机器学习之聚类——模糊聚类FCM

FCM

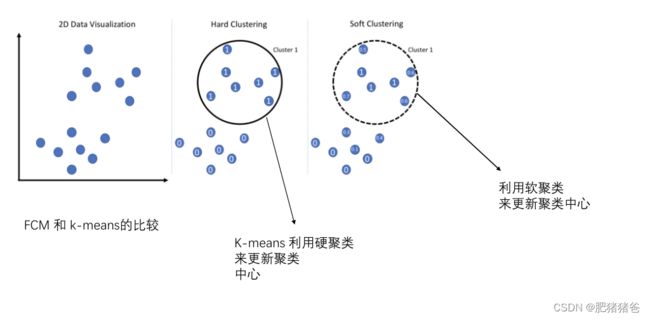
FCM，英文全程Fuzzy C-Means(FCM)，是一种基于目标函数的模糊聚类方法。

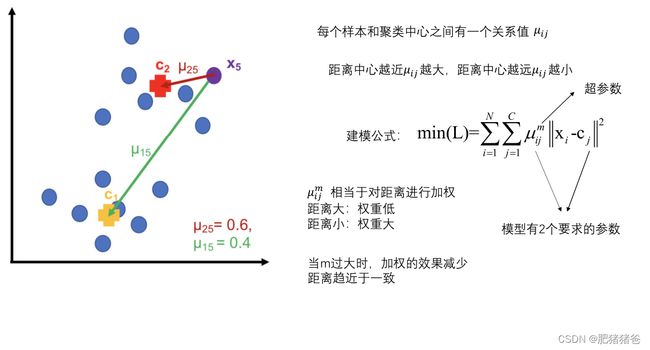
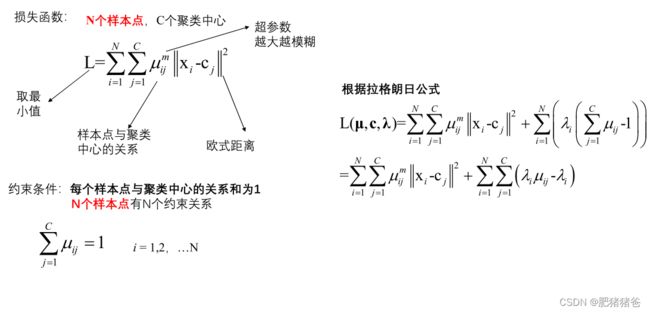
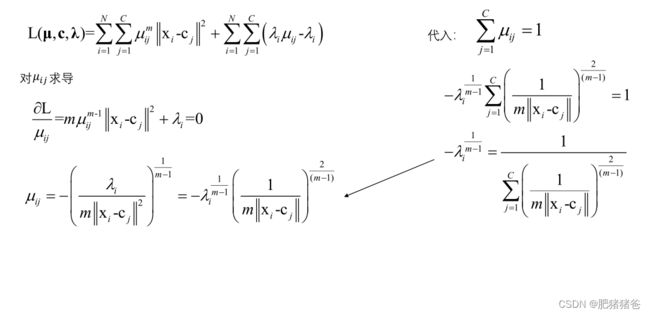
原理

关于FCM的资料，网上很多，原理也相对简单，详述如下

代码

import numpy as np
from matplotlib import pyplot as plt


class FCM:
    def __init__(self, K, m=2, eps=0.1):
        # 聚类个数
        self.K = K
        # 加权参数
        self.m = m
        # 终止容限
        self.eps = eps
        # 最优相似度矩阵
        self.U = None
        # 最终的聚类中心
        self.centers = None

    def train(self, data):
        # 初始化隶属度矩阵
        self.U = np.random.random((len(data), self.K))
        # 保证每个样本属于所有类的概率是1
        self.U = np.divide(self.U, np.sum(self.U, axis=1)[:, np.newaxis])

        while True:
            temp_U = self.U ** self.m
            # 计算聚类中心
            self.centers = np.divide(np.dot(temp_U.T, data), np.sum(temp_U.T, axis=1)[:, np.newaxis])
            # 样本到聚类中心的距离
            dist = np.zeros((len(data), self.K))
            for i, x in enumerate(data):
                for j, c in enumerate(self.centers):
                    dist[i][j] = np.linalg.norm(x - c, 2)
            # 计算新的隶属度矩阵
            for i, x in enumerate(data):
                for j, c in enumerate(self.centers):
                    temp_U[i][j] = 1./np.sum((dist[i][j]/dist[i]) ** (2/(self.m-1)))
            # 判断是否收敛
            if np.sum(abs(temp_U-self.U)) < self.eps:
                break
            # 更新隶属度矩阵
            self.U = temp_U
        # 返回样本最大隶属度对应的类别
        return np.argmax(self.U, axis=1)

    def __str__(self) -> str:
        return f"K：{self.K}, m：{self.m}, eps：{self.eps}, U：{self.U}, centers：{self.centers}"


if __name__ == "__main__":
    # 样本数量
    N = 3000
    # 测试数据
    X = np.concatenate((
        np.random.normal((-2, -2), size=(N, 2)),
        np.random.normal((2, 2), size=(N, 2))
    ))
    # 模型
    fcm = FCM(K=2, m=2, eps=1)
    # 训练
    y = fcm.train(X)
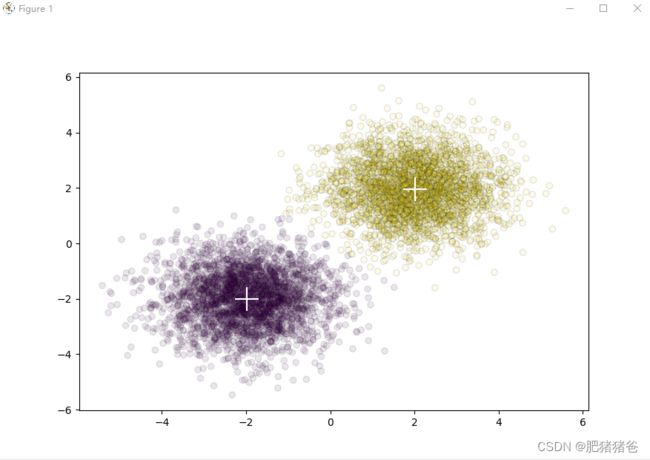
    # 绘图
    plt.scatter(X[:, 0], X[:, 1], c=y, alpha=.1, edgecolors='black')
    plt.scatter(fcm.centers[:, 0], fcm.centers[:, 1], marker="+", s=500, c='w')
    plt.show()

运行效果如图：

作者这水平有限，有不足之处欢迎留言指正