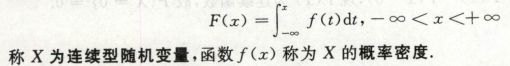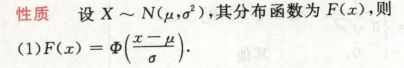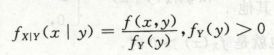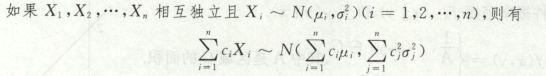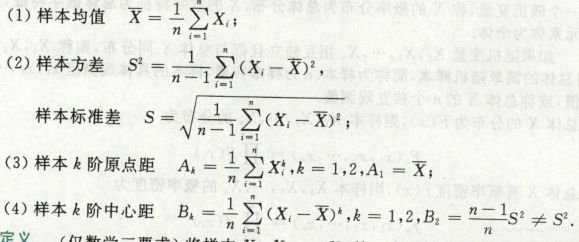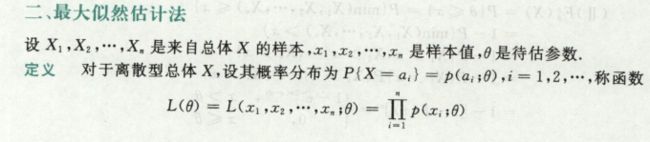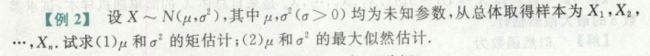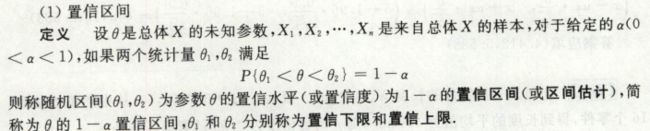概率论-基础篇笔记(更完)

第一章 随机事件和概率

事件的关系与运算

事件关系：
包含（a包含b，说明b发生a一定发生）
相等
交、并、补
互斥
对立
差（A-B = A-AB = A$\overline{\text{B}}$）

---

事件运算律
交换、结合、分配律
对偶律：
$\overline{\text{A∪B}}=\overline{\text{A}}\cap \overline{\text{B}}$

$A\supset B=\overline{\text{A}}\subset \overline{\text{B}}$

概率及概率公式

两两独立 ≠ 相互独立

独立只和概率有关，和事件无关，概率推不出事件

---

五大概率公式

全概率公式 见贝叶斯公式的分母部分

AB独立时，常用结论：

---

古典概型和伯努利实验

第二章 随机变量及其概率分布

随机变量和其分布函数

P(X=x)=Fx右极限- 左极限
右连续 = F(x⁺) = F(x)
记住简化部分，+一个Fx∈[0,1]

常用分布

0-1分布
几何和超几何分布
略

---

二项分布

X~B(1,p)

X~B(2,p)

---

泊松分布

和e^x的泰勒公式联系

---

常考：
P = 底边 * 高

---

指数分布

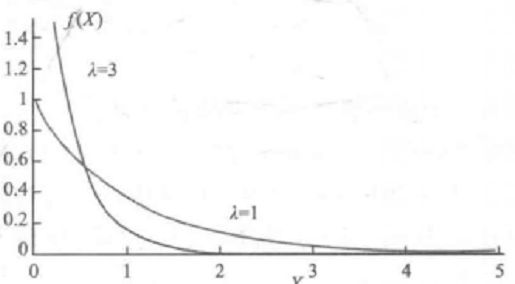
指数分布的概率密度

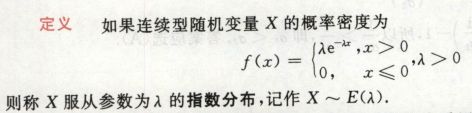
指数分布的分布函数

两个性质
要直接记住：

---

正态分布概率密度

分布函数就是概率密度的积分，写不出来

性质：
考4个地方（一般多个考点综合）（查表这几年不怎么考了）

1.查表
2.标准化
3.对称性
4.定参数

标准化

标准化2

对称性3个

5要直接记住

随机变量函数的分布

引入

离散的比较简单

连续型用公式法做，看例题，3个考点：分布函数定义（写出公式就有2分）、随机变量范围、端点
随机变量范围：如这题的

Y=X²+1，可以求得Y∈[1,2]，那么Y<1时Fy=0，Y>2时Fy=1

常用结论：

第三章 多维随机变量及其分布

二维随机变量及其分布

性质：
F（X,Y）的有界性：F（X,Y）实质仍然是一个概率，范围在[0，1]之间。

F（-∞, -∞）=0，F（+∞,+∞）=1。

F（X,Y）的单调性：F（X,Y）关于X,Y均属于单调不减函数。

F（X,Y）连续性：右连续。

计算公式:

边缘分布

---

二维离散随机变量

性质

边缘分布：

算X，y相加，
算Y，x相加

条件分布：

---

二维连续型随机变量

X、Y的联合概率密度

性质3每年都考

掌握好边缘密度，求X，对y积分，求Y对x积分

条件密度，这几年考的多

条件分布

例题：重点
第一问求边缘分布，就是积分，考点是定义、范围、端点
第二问直接考的定义

2013年数三，大其他和小其他

随机变量的独立性

类似于事件A和B的独立，只是变成了随机变量

离散随机变量的独立

连续型随机变量独立

二维均匀分布和二维正态分布

二维均匀分布还是求的面积

A=S

---

二维正态分布

性质：

二维正态分布的两个边缘分布都是一维正态分布的形式

对于二维正态随机变量（X，Y），X和Y相互独立的充要条件是参数ρ=0

两个随机变量函数Z=g(X,Y)的分布

XY均为离散型，比较简单，略

---

XY均为连续型

卷积公式

---

XY 一个连续一个离散

用全概率公式

---

常用结论：
max{X,Y}

例题

---

min{X,Y}

例题：

另一种思路

第四章 随机变量的数字特征

随机变量的数学期望和方差

离散

连续

四个性质

性质4补充：不相关即可，E(XY) = E(X)E(Y)

性质3的推广，累加∑提出：
Xi是独立同分布，E(∑Xi) = ∑E(Xi)

---

随机变量函数的期望

把x换成g(x)，但概率函数还是用的X的

二维的

---

方差
EX = μ，DX = E[(X - μ)²]

⚠重点：
计算公式：D(X) = E(X²) - (EX)²
常用计算：E(X²) = σ² + μ²

性质:

1. D(aX+b) = a² · D(X)

2. XY独立（或者不相关）
   D(X±Y) = D(X) + D(Y)

3. D(a)=0

---

常用随机变量的数学期望和方差

协方差和相关系数

这个协方差可以看成是随机变量X和Y的原点距离之间相关性，最基础的相关性就是A · B了

计算公式

性质：

---

相关系数

---

独立与不相关

1. 独立一定不相关，反之不一定

2. 二维正态：独立和不相关等价 <=> 相关系数ρ=0
   

---

常用相关结论

第五章 大数定律和中心极限定理

切不

依概率收敛

切大

Xi不相关，方差有界，1/n∑Xi -> 1/n∑E(Xi)

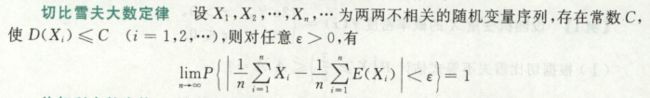
辛大

Xi独立同分布，期望EX = μ，1/n∑Xi -> μ

林中

Xi独立同分布，EX = μ， DX=σ²

∑Xi - nμ / 根号下nDX ~ N(0,1)

第六章 数理统计的基本概念

总体、样本、统计量和样本数字特征

---

样本的联合分布和概率密度，核心是累乘，公式略

---

统计量

常用统计量

12常考，34一般用在点估计上（3一阶，4二阶）

---

常用统计量的性质

1. EX^-bar = EX
2. DX^-bar = DX/n
3. E(S²) = DX

例题：

常用统计分布抽样分布

卡方分布

Xi~N(0,1)且相互独立

性质：


分位点和概率密度

---

t分布

X服从正态分布，Y是卡方分布

性质：

1. 偶函数
   
2. 概率密度函数及分位点
   
   
   

---

F分布

X~卡方(n1)
Y~卡方(n2)
XY相互独立
F~F(n1,n2)

性质：

---

要点说明，三个分布都要求R.V之间相互独立，卡方考EX和DX，t分布考偶函数性质，F分布，1/F ~ F(n2,n1)

正态总体的抽样分布

123要记，4只是标准化而已

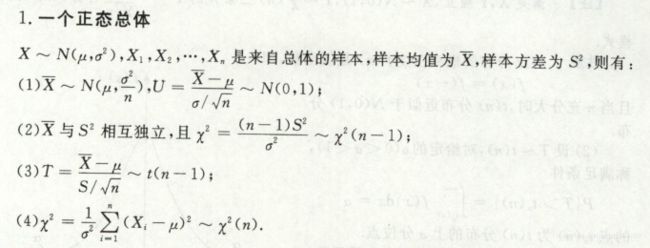
(n-1) · S² = ∑(Xi - X^-bar)²

例题：

考点：t分布定义，F分布定义，t分布性质

第七章 参数估计

这一章是重点！基本上等于必考

点估计

用样本Xi……去估计参数θ，其构造的θ统计量称为（估计量）θ^-hat

---

无偏估计

E(S²) = DX

常用公式

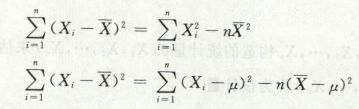
(n-1) · S² = ∑(Xi - X^-bar)² = ∑Xi² - nX-bar²

---

---

一致估计量

---

估计量的求法和区间估计

矩估计

一阶原点矩 EX = μ => μ^-hat = X^-bar
二阶原点矩 E(X²) = DX + (EX)² = σ² + μ² = 1/n∑Xi²
二阶中心矩：
D(X)=E{[X-E(X)]²} = 1/n∑(Xi - μ)²
DX^-hat = 1/n∑(Xi - X^-bar)²

最大似然估计

一般求法

例题：

区间估计

3-5年考一次

---

置信区间

---

第八章 假设检验

基本没考过

---

第一类错误：拒真
第二类错误：纳伪

拒真的意思是：
在基本假设H0的条件下，X却落在对立假设H1区间中，
我们称这个概率P为显著水平/检验水平，这个概率经常要求控制在α以下，α一般=0.05
置信水平为1-α，在基本假设H0的条件下，X确实落在H0区间中的概率

---

一般步骤

---

检验参数μ的情况：

例题：
(D)

---

公式补充

∫ xⁿ · e^-xdx = n!

=>I1 = ∫ x · e^-xdx = 1

---

∫ e^{-x^2} dx = 根号Π

---