《剑指offer》Java版题解:动态规划篇一
目录
前言
一、JZ42 连续子数组的最大和
二、JZ85 连续子数组的最大和(二)
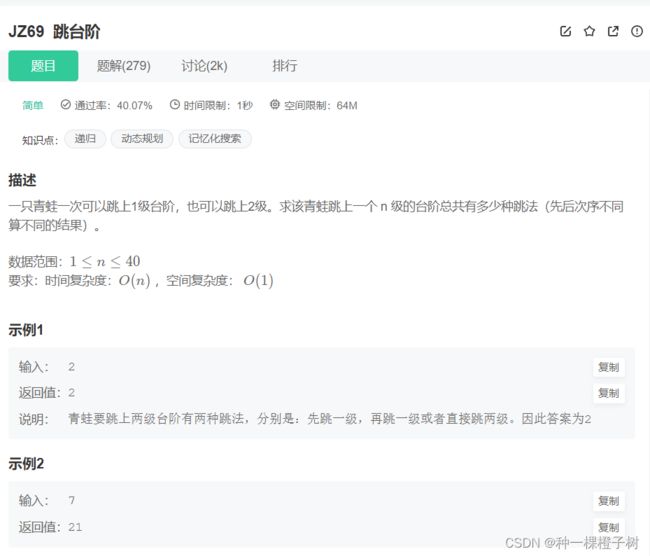
三、跳台阶
四、JZ10 斐波那契数列
五、JZ71 跳台阶扩展问题
六、JZ70 矩形覆盖
总结
前言
本篇文章记录本人练习《剑指offer》动态规划篇的心得与体会,题目来源于牛客网,语言选用Java,如有提议和建议,欢迎在评论区不吝赐教。感谢~
一、JZ42 连续子数组的最大和
题解思路:
这题如果不使用动态规划的思想的话,我们可以通过两次循环遍历来暴力解决。也就是两次for循环记录所有子数组相加的值,然后设一个sum变量,始终记录最大的子数组相加值,然后输出。
代码如下:
public int FindGreatestSumOfSubArray(int[] array) {
int max = array[0];
int sum = 0;
for(int i=0;i这种写法思路很简单,但是时间复杂度为O(n²)不建议使用
思路二:动态规划的思想,我们只需要设置两个变量,sum和max ,sum用来保存当前子序列的最大值,而max用于保存所有子序列中的最大值。先上代码,我们结合代码分析。
public class Solution {
public int FindGreatestSumOfSubArray(int[] array) {
int sum = array[0];
int max = array[0];
for(int i =1;i此图片来源于牛客网解答leaves0924大神~
首先我们默认最大子数组的和就是array[0]的值,当前最大子数组的和也是array[0],这样我们从数组下标1开始遍历,每一次我们判断sum+当前元素和当前元素的大小。意思就是,如果我们之前的子数组合加上当前元素都比当前元素小了,那我们不如就直接从当前元素开始重新作为子数组的第一个元素再进行大小判断。另外max始终负责存储最大子数组和,所有我们输出的时候只要输出max就行了。这样就完成了,时间复杂度O(n) 空间复杂度O(1)
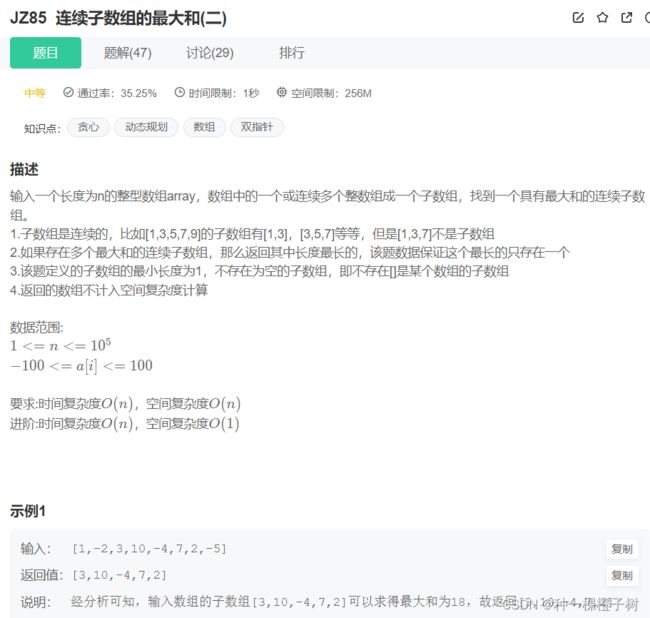
二、JZ85 连续子数组的最大和(二)
首先看题意,这道题相比上一题的改动无非就是让我们输出最大长度的子数组。
注意了,这里要求的是输出最大长度,也就是说,可能有两个子数组的最大和是相同的,但是我们要输出最长的那一个。
所以我们可以大致的思路就是,当我们碰到有相同大小的子数组和的时候,我们比较一下两个子数组的长度,让最大数组是最长的那个就行了。
这里我们新建一个数组dp,dp用于保存最长子数组的和。
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param array int整型一维数组
* @return int整型一维数组
*/
public int[] FindGreatestSumOfSubArray (int[] array) {
// write code here
int maxSum = array[0];
int[] dp = new int[array.length];
dp[0] = array[0];
int maxLength = 1,left = 0,right = 0,dpleft = 0,dpright = 0;
for(int i =1;imaxSum || dp[i] == maxSum && (right-left+1)>maxLength){
dpleft = left;
dpright = right;
maxLength = right - left + 1;
maxSum = dp[i];
}
}
int[] res = new int[maxLength];
int index = 0;
for(int i = dpleft;i<=dpright;i++){
res[index++] = array[i];
}
return res;
}
} 三、跳台阶
经典问题,青蛙跳台阶。
看完题目后,我们会发现,青蛙跳台阶的过程和斐波拉契数列是很像的(感兴趣的可以自行了解)
可能很多人的第一想法会跟我一样...我们设想青蛙从地上开始第一次跳一级台阶,或者两级台阶,然后再往下分析。。。
但其实我们逆向思维想一下,加入我们现在在第n级台阶上,那么青蛙只有可能是从第n-1,或者n-2级台阶跳过来的。
换种话说,我们设跳上第n个台阶 有f(n)种方法,而我们要跳上第n个台阶 只可能是在第n-1的台阶上跳一及,还有就是在第n-2的台阶上跳两级。那我们可以看出f(n)= f(n-1)+f(n-2)
这规律就找出来啦,根据规律,我们第一个最容易想到的办法就是递归。
class Solution {
public:
int jumpFloor(int number) {
if(number<=1) return 1;
return jumpFloor(number-1)+jumpFloor(number-2);
}
};递归的方式代码很简洁,很暴力,终止条件就是f(1)因为我们跳上第一级台阶只有一种方式。
递归的时间复杂度比较高O(2^n)。所以我们还有另一种方法。
递归的时间复杂度高,主要是我们需要多次遍历之前已经算出来的第n级台阶有多少种跳法,所以我们优化的思路就是,既然我们计算第n个台阶的跳法,只需要n-1和n-2台阶的跳法就行了,那我们能不能每次保存上一个台阶的跳法和上上个台阶的跳法呢,当然是可以的。
直接上代码拉,不讲多了 好长喔。
public class Solution {
public int jumpFloor(int target) {
if(target<=2){
return target;
}
int sum = 0;
int first = 1,second = 2;
for(int i = target;i>2;i--){
sum = first+second;
first = second;
second = sum;
}
return sum;
}
}四、JZ10 斐波那契数列
这就没啥好讲的了,规律都给了,直接上图上代码。注意临界条件就行。
public class Solution {
int sum = 0;
public int Fibonacci(int n) {
int first = 1,second = 1;
if(n<=2){
sum = 1;
}
for(int i = n;i>2;i--){
sum = first + second;
first = second;
second = sum;
}
return sum;
}
} 五、JZ71 跳台阶扩展问题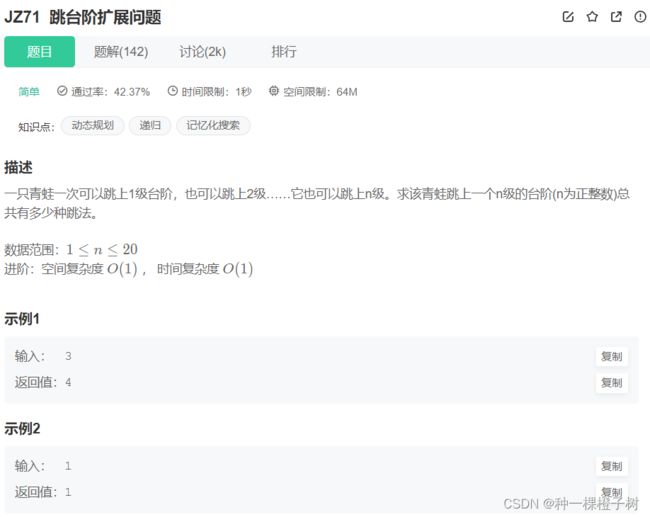
没错!还是那只青蛙,只不过这只青蛙增强了!他现在能一次性跳n级台阶。
规律就是f(n)=f(n-1)+f(n-2)+f(...)+f(1) f(n)=2*f(n-1)
public class Solution {
int sum = 0;
public int jumpFloorII(int target) {
if(target<=2){
return target;
}
int first = 1,second = 2;
for(int i = target;i>2;i--){
sum = 2*second;
first = second;
second = sum;
}
return sum;
}
}六、JZ70 矩形覆盖
这题,也没啥好说的,还是青蛙跳台阶问题。
n=1 我们只有一种方式,n=2,我们有两种,n=3,我们可以看成是先做n=1,然后再加上n=2。
所以这就又回到了f(n)= f(n-1)+f(n-2)问题。
说句题外话,其实我感觉动态规划篇章的题目很多都是找到规律就有了思路,重点是我们写这一类题目的思路。
上代码!!
public class Solution {
int sum = 0;
public int rectCover(int target) {
if(target == 0){
return 0;
}
if(target==1){
return 1;
}
if(target == 2){
return 2;
}
int first = 1,second =2;
for(int i = target;i>2;i--){
sum = first+second;
first = second;
second = sum;
}
return sum;
}
}
总结
好了,由于篇幅原因,本次先记录这么多,下一次补齐~,首先声明,本人也是一只菜鸟,算法也才刚开始接触,如果有更高的见解,请不吝赐教私信本人,评论也可以。我将万分感激,谢谢。