逻辑回归算法

逻辑回归又叫logistic回归分析，是一种广义的线性回归分析模型。线性回归要求因变量必须是连续性的数据变量，逻辑回归要求因变量必须是分类变量，可以是二分类或者多分类(多分类都可以归结到二分类问题)，逻辑回归的输出是0~1之间的概率。比如要分析年龄，性别，身高，饮食习惯对于体重的影响，如果体重是实际的重量，那么就要使用线性回归。如果将体重分类，分成了高，中，低三类，就要使用逻辑回归进行分类。

逻辑回归公式： 

逻辑回归公式又叫逻辑函数（Logistic function）或者S形函数（Sigmoid function）。逻辑回归公式的图像如下：

即当z=0时，f(z) =0.5，当z->无穷大 时，趋近于1，当z->无穷小时，趋近于0。逻辑回归的输出就是位于0~1之间的概率，假设现在判断病人是否生病，得到的z=2对应的=0.7我们可以归结为生病，如果z=-2对应的=0.1我们就可以认为不生病。当z=0时，=0.5是决策的边界。

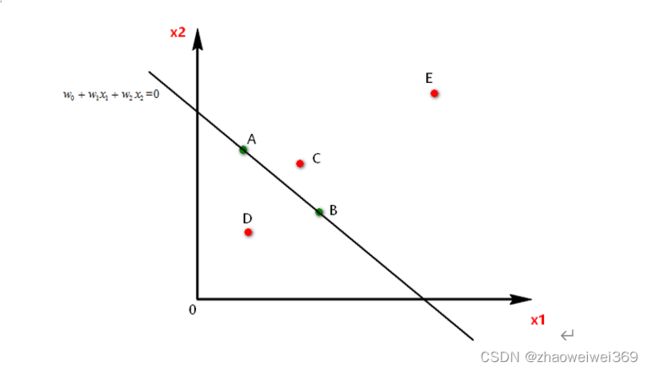
假设都大于零，那么当z=0时，f(z)=0.5。也就是时，=0.5，当z=0时使用图像来表达两个自变量的关系为： 

图中A、B、C、D、E点都表示有x1，x2两个维度的数据，现要使用逻辑回归对五个点分成两类：I和II类，A点和B点都在直线上，对应的z值是0，那么逻辑回归结果f(z)=0.5，将A,B两点划分为I类和II类都可以，假设我们规定当z>=0属于I类，z<0属于II类，那么A,B属于I类。C点位于直线的上方，对应的z值要大于零，反映到S形函数上对应的>0.5属于I类，同理，E也属于I类，D点属于II类。图中E点的z值远大于C点的z值，反映到S形函数中，E点属于I类的概率比C点属于I类的概率要大的多。训练逻辑回归模型，在这里就是训练出一条直线将两个类别的点隔开。如果维度是3,那么训练逻辑回归模型就是训练一个平面将两个类别的点隔开。如果维度大于3,那么训练逻辑回归模型就是训练一个超平面将两个类别的点隔开。 

音乐分类案例

1. 傅里叶变换：

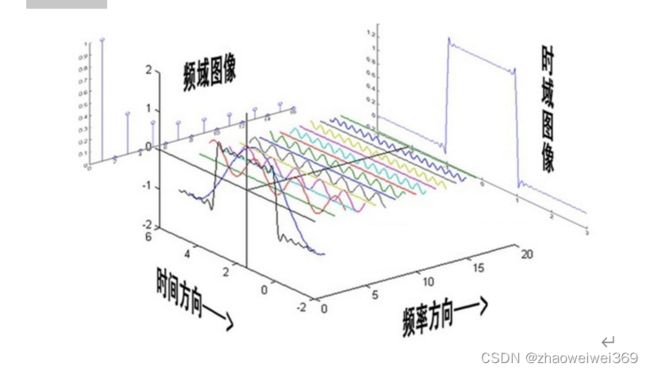
时域分析：对一个信号来说，信号强度随时间的变化的规律就是时域特性，例如一个信号的时域波形可以表达信号随着时间的变化。

频域分析：对一个信号来说，在对其进行分析时，分析信号和频率有关的部分，而不是和时间相关的部分，和时域相对。也就是信号是由哪些单一频率的的信号合成的就是频域特性。频域中有一个重要的规则是正弦波是频域中唯一存在的波。即正弦波是对频域的描述，因为时域中的任何波形都可用正弦波合成。

一般来说，时域的表示较为形象直观，频域分析则简练。傅里叶变换是贯穿时域和频域的方法之一，傅里叶变换就是将难以处理的时域信号转换成了易于分析的频域信号。傅里叶原理：任何连续测量的时序信号，都可以表示为不同频率的正弦波信号的无限叠加。

2. 音乐分类的步骤:

1. 通过傅里叶变换将不同7类里面所有原始wav格式音乐文件转换为特征,并取前1000个特征,存入文件以便后续训练使用
2. 读入以上7类特征向量数据作为训练集
3. 使用sklearn包中LogisticRegression的fit方法计算出分类模型
4. 读入黑豹乐队歌曲”无地自容”并进行傅里叶变换同样取前1000维作为特征向量
5. 调用模型的predict方法对音乐进行分类,结果分为rock即摇滚类

from scipy import fft
from scipy.io import wavfile
from scipy.stats import norm
from sklearn import linear_model, datasets
from sklearn.linear_model import LogisticRegression

import matplotlib.pyplot as plt
import numpy as np
"""
使用logistic regression处理音乐数据,音乐数据训练样本的获得和使用快速傅里叶变换（FFT）预处理的方法需要事先准备好
1. 把训练集扩大到每类100个首歌,类别仍然是六类:jazz,classical,country, pop, rock, metal
2. 同时使用logistic回归训练模型
3. 引入一些评价的标准来比较Logistic测试集上的表现 
"""
# 准备音乐数据
def create_fft(g,n):
    rad="i:/genres/"+g+"/converted/"+g+"."+str(n).zfill(5)+".au.wav"
    (sample_rate, X) = wavfile.read(rad)
    #取1000个频率特征
    fft_features = abs(fft(X)[:1000])
    #zfill(5) 字符串不足5位，前面补0
    sad="i:/trainset/"+g+"."+str(n).zfill(5)+ ".fft"
    np.save(sad, fft_features)
genre_list = ["classical", "jazz", "country", "pop", "rock", "metal","hiphop"]
for g in genre_list:
    for n in range(100):
        create_fft(g,n)
        print 'running...'
print 'finished'
read fft-------------- 
genre_list = ["classical", "jazz", "country", "pop", "rock", "metal","hiphop"]
X=[]
Y=[]
for g in genre_list:
    for n in range(100):
        rad="i:/trainset/"+g+"."+str(n).zfill(5)+ ".fft"+".npy"
        fft_features = np.load(rad)
        X.append(fft_features)
        #genre_list.index(g) 返回匹配上类别的索引号
        Y.append(genre_list.index(g))
  
#构建的训练集
X=np.array(X)
#构建的训练集对应的类别
Y=np.array(Y)
-----train logistic classifier-------------- 
model = LogisticRegression()
#需要numpy.array类型参数
model.fit(X, Y)
  
print 'Starting read wavfile...'
#prepare test data-------------------
sample_rate, test = wavfile.read("i:/classical.00007.au.wav")
# sample_rate, test = wavfile.read("i:/heibao-wudizirong-remix.wav")
testdata_fft_features = abs(fft(test))[:1000]
type_index = model.predict(testdata_fft_features)[0]
print type_index
print genre_list[type_index]