pytorch框架下—GCN代码详细解读

说明：本文是对论文“SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS， ICLR 2017”中描述的GCN模型代码的详细解读。
代码下载地址：https://github.com/tkipf/pygcn
论文下载地址：https://arxiv.org/abs/1609.02907
数据集下载地址：https://linqs-data.soe.ucsc.edu/public/lbc/cora.tgz

---

代码结构总览

作为图神经网络的入门级代码，该代码相对来说结构简单。代码总共包含四个部分：

此处的代码结构图参考了CSDN博客“Graph Convolution Network图卷积网络（一）训练运行与代码概览”

• utils：定义了加载数据等工具性的函数
• layers：定义了模块如何计算卷积
• models：定义了模型train
• train：包含了模型训练信息
  

一、数据集结构、内容分析

1、数据集结构

论文中所使用的数据集合是Cora数据集，总共有三部分构成：cora.content cora.cites 和README。

README： 对数据集内容的描述；

cora.content： 里面包含有每一篇论文各自独立的信息；

该文件总共包含2078行，每一行代表一篇论文，由论文编号、论文词向量（1433维）和论文的类别三个部分组成

cora.cites: 里面包含有各论文之间的相互引用记录

该文件总共包含5429行，每一行是两篇论文的编号，表示右边的论文引用左边的论文。

2、数据集内容分析

该数据集总共有2078个样本，而且每个样本都为一篇论文。根据README可知，所有的论文被分为了7个类别，分别为：

1. 基于案列的论文
2. 基于遗传算法的论文
3. 基于神经网络的论文
4. 基于概率方法的论文
5. 基于强化学习的论文
6. 基于规则学习的论文
7. 理论描述类的论文

此外，为了区分论文的类别，使用一个1433维的词向量，对每一篇论文进行描述，该向量的每个元素都为一个词语是否在论文中出现，如果出现则为“1”，否则为“0”。

二、utils代码分析

1、代码总览

import numpy as np
import scipy.sparse as sp
import torch


def encode_onehot(labels):
    classes = set(labels)
    classes_dict = {c: np.identity(len(classes))[i, :] for i, c in
                    enumerate(classes)}
    labels_onehot = np.array(list(map(classes_dict.get, labels)),
                             dtype=np.int32)
    return labels_onehot


def load_data(path="../data/cora/", dataset="cora"):
    """Load citation network dataset (cora only for now)"""
    print('Loading {} dataset...'.format(dataset))

    idx_features_labels = np.genfromtxt("{}{}.content".format(path, dataset),
                                        dtype=np.dtype(str))
    features = sp.csr_matrix(idx_features_labels[:, 1:-1], dtype=np.float32)
    labels = encode_onehot(idx_features_labels[:, -1])

    # build graph
    idx = np.array(idx_features_labels[:, 0], dtype=np.int32)
    idx_map = {j: i for i, j in enumerate(idx)}
    edges_unordered = np.genfromtxt("{}{}.cites".format(path, dataset),
                                    dtype=np.int32)
    edges = np.array(list(map(idx_map.get, edges_unordered.flatten())),
                     dtype=np.int32).reshape(edges_unordered.shape)
    adj = sp.coo_matrix((np.ones(edges.shape[0]), (edges[:, 0], edges[:, 1])),
                        shape=(labels.shape[0], labels.shape[0]),
                        dtype=np.float32)

    # build symmetric adjacency matrix
    adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)

    features = normalize(features)
    adj = normalize(adj + sp.eye(adj.shape[0]))

    idx_train = range(140)
    idx_val = range(200, 500)
    idx_test = range(500, 1500)

    features = torch.FloatTensor(np.array(features.todense()))
    labels = torch.LongTensor(np.where(labels)[1])
    adj = sparse_mx_to_torch_sparse_tensor(adj)

    idx_train = torch.LongTensor(idx_train)
    idx_val = torch.LongTensor(idx_val)
    idx_test = torch.LongTensor(idx_test)

    return adj, features, labels, idx_train, idx_val, idx_test


def normalize(mx):
    """Row-normalize sparse matrix"""
    rowsum = np.array(mx.sum(1))
    r_inv = np.power(rowsum, -1).flatten()
    r_inv[np.isinf(r_inv)] = 0.
    r_mat_inv = sp.diags(r_inv)
    mx = r_mat_inv.dot(mx)
    return mx


def accuracy(output, labels):
    preds = output.max(1)[1].type_as(labels)
    correct = preds.eq(labels).double()
    correct = correct.sum()
    return correct / len(labels)


def sparse_mx_to_torch_sparse_tensor(sparse_mx):
    """Convert a scipy sparse matrix to a torch sparse tensor."""
    sparse_mx = sparse_mx.tocoo().astype(np.float32)
    indices = torch.from_numpy(
        np.vstack((sparse_mx.row, sparse_mx.col)).astype(np.int64))
    values = torch.from_numpy(sparse_mx.data)
    shape = torch.Size(sparse_mx.shape)
    return torch.sparse.FloatTensor(indices, values, shape)

2、特征独热码处理

在很多的多分类问题中，特征的标签通常都是不连续的内容（如本文中特征是离散的字符串类型），为了便于后续的计算、处理，需要将所有的标签进行提取，并将标签映射到一个独热码向量中。

def encode_onehot(labels):
    #将所有的标签整合成一个不重复的列表
    classes = set(labels)   # set() 函数创建一个无序不重复元素集

    '''enumerate()函数生成序列，带有索引i和值c。
    这一句将string类型的label变为int类型的label，建立映射关系
    np.identity(len(classes)) 为创建一个classes的单位矩阵
    创建一个字典，索引为 label， 值为独热码向量（就是之前生成的矩阵中的某一行）'''
    classes_dict = {c: np.identity(len(classes))[i, :] for i, c in
                    enumerate(classes)}
    # 为所有的标签生成相应的独热码
    # map() 会根据提供的函数对指定序列做映射。
    # 这一句将string类型的label替换为int类型的label
    labels_onehot = np.array(list(map(classes_dict.get, labels)),
                             dtype=np.int32)
    return labels_onehot

输入labels为：

执行完该程序后，输出的独热码为：

3、特征归一化函数

该函数需要传入特征矩阵作为参数。对于本文使用的cora的数据集来说，每一行是一个样本，每一个样本是1433个特征。

需要注意的是：由于特征中有很多的内容是“0”，因此使用稀疏矩阵的方式进行存储，因此经过该函数归一化之后的函数，仍然为一个稀疏矩阵。

归一化函数实现的方式：对传入特征矩阵的每一行分别求和，取到数后就是每一行非零元素归一化的值，然后与传入特征矩阵进行点乘。

def normalize(mx):
    rowsum = np.array(mx.sum(1)) #会得到一个（2708,1）的矩阵
    r_inv = np.power(rowsum, -1).flatten() #得到（2708，）的元祖
    #在计算倒数的时候存在一个问题，如果原来的值为0，则其倒数为无穷大，因此需要对r_inv中无穷大的值进行修正，更改为0
    r_inv[np.isinf(r_inv)] = 0.
    r_mat_inv = sp.diags(r_inv)
    mx = r_mat_inv.dot(mx)
    return mx

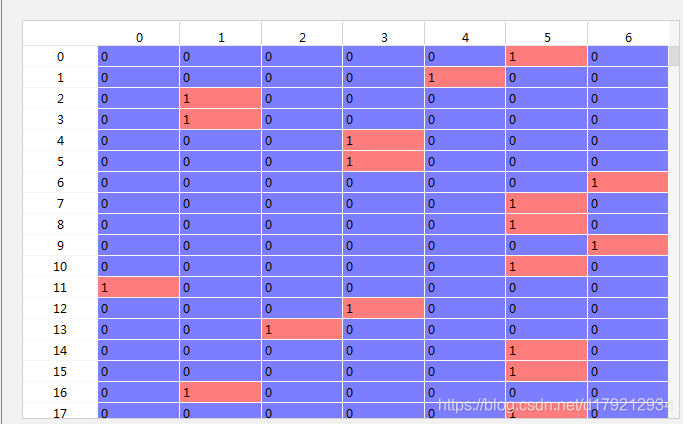
本文中以领接矩阵作为示例说明上述问题，其输入矩阵mx如图所示：

归一化之后输出的内容为：

4、稀疏矩阵转稀疏张量函数

def sparse_mx_to_torch_sparse_tensor(sparse_mx):
    """Convert a scipy sparse matrix to a torch sparse tensor."""
    """
    numpy中的ndarray转化成pytorch中的tensor : torch.from_numpy()
    pytorch中的tensor转化成numpy中的ndarray : numpy()
    """
    sparse_mx = sparse_mx.tocoo().astype(np.float32)
    indices = torch.from_numpy(
                np.vstack((sparse_mx.row, sparse_mx.col)).astype(np.int64))
    values = torch.from_numpy(sparse_mx.data)
    shape = torch.Size(sparse_mx.shape)
    return torch.sparse.FloatTensor(indices, values, shape)

5、精度计算函数

def accuracy(output, labels):
    # 使用type_as(tesnor)将张量转换为给定类型的张量。
    preds = output.max(1)[1].type_as(labels)
    # 记录等于preds的label eq:equal
    correct = preds.eq(labels).double()
    correct = correct.sum()
    return correct / len(labels)

6、数据载入及处理函数

def load_data(path="data/cora/", dataset="cora"):
    """Load citation network daraser (cora only for now)"""
    print('Loading {} dataset...'.format(dataset))
    #首先将文件中的内容读出，以二维数组的形式存储
    idx_features_labels = np.genfromtxt("{}{}.content".format(path,dataset), dtype=np.dtype(str))
    #以稀疏矩阵（采用CSR格式压缩）将数据中的特征存储
    features = sp.csr_matrix(idx_features_labels[:, 1:-1], dtype=np.float32)
    # label
    labels = encode_onehot(idx_features_labels[:, -1])

    """根据引用文件，生成无向图"""

    # 将每篇文献的编号提取出来
    idx = np.array(idx_features_labels[:, 0], dtype = np.int32)
    # 对文献的编号构建字典
    idx_map = {j : i for i, j in enumerate(idx)}
    #读取cite文件
    edges_unordered = np.genfromtxt("{}{}.cites".format(path,dataset), dtype=np.int32)
    # 生成图的边，（x,y）其中x、y都是为以文章编号为索引得到的值，此外，y中引入x的文献
    edges = np.array(list(map(idx_map.get,edges_unordered.flatten())), dtype = np.int32).reshape(edges_unordered.shape)
    #生成领接矩阵，生成的矩阵为稀疏矩阵，对应的行和列坐标分别为边的两个点，该步骤之后得到的是一个有向图
    adj = sp.coo_matrix((np.ones(edges.shape[0]), (edges[:,0],edges[:,1])), shape=(labels.shape[0],labels.shape[0]),dtype = np.float32)

    #无向图的领接矩阵是对称的，因此需要将上面得到的矩阵转换为对称的矩阵，从而得到无向图的领接矩阵
    '''
    论文中采用的办法和下面两个语句是等价的，仅仅是为了产生对称的矩阵
    adj_2 = adj + adj.T.multiply(adj.T > adj)
    adj_3 = adj + adj.T
    '''
    adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)
    
    #进行归一化，对应于论文中的A^=(D~)^0.5 A~ (D~)^0.5,但是本代码实现的是A^=(D~)^-1 A~
    #A^=I+A
    adj = normalize(adj + sp.eye(adj.shape[0]))

    # 分别构建训练集、验证集、测试集，并创建特征矩阵、标签向量和邻接矩阵的tensor，用来做模型的输入
    idx_train = range(140)
    idx_val = range(200, 500)
    idx_test = range(500, 1500)
    # 将特征转换为tensor
    features = torch.FloatTensor(np.array(features.todense()))
    labels = torch.LongTensor(np.where(labels)[1])
    adj = sparse_mx_to_torch_sparse_tensor(adj)

    
    idx_train = torch.LongTensor(idx_train)
    idx_val = torch.LongTensor(idx_val)
    idx_test = torch.LongTensor(idx_test)

    return adj, features, labels, idx_train, idx_val, idx_test

三、models代码分析

1、代码总览

import torch.nn as nn
import torch.nn.functional as F
from pygcn.layers import GraphConvolution


class GCN(nn.Module):
    def __init__(self, nfeat, nhid, nclass, dropout):
        super(GCN, self).__init__()

        self.gc1 = GraphConvolution(nfeat, nhid)
        self.gc2 = GraphConvolution(nhid, nclass)
        self.dropout = dropout

    def forward(self, x, adj):
        x = F.relu(self.gc1(x, adj))
        x = F.dropout(x, self.dropout, training=self.training)
        x = self.gc2(x, adj)
        return F.log_softmax(x, dim=1)

2、代码分析

class GCN(nn.Module)定义了一个图卷积神经网络，其有两个卷积层：

• 卷积层1：输入的特征为nfeat，维度是2708，输出的特征为nhid，维度是16；
• 卷积层2：输入的特征为nhid，维度是16，输出的特征为nclass，维度是7（即类别的结果）

forward是向前传播函数，最终得到网络向前传播的方式为：relu–>fropout–>gc2–>softmax

四、layers代码分析

1、代码总览

layers中主要定义了图数据实现卷积操作的层，类似于CNN中的卷积层，只是一个层而已。本节将分别通过属性定义、参数初始化、前向传播以及字符串表达四个方面对代码进一步解析。

import math
import torch

from torch.nn.parameter import Parameter
from torch.nn.modules.module import Module


class GraphConvolution(Module):
    """
    Simple GCN layer, similar to https://arxiv.org/abs/1609.02907
    """

    def __init__(self, in_features, out_features, bias=True):
        super(GraphConvolution, self).__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.weight = Parameter(torch.FloatTensor(in_features, out_features))
        if bias:
            self.bias = Parameter(torch.FloatTensor(out_features))
        else:
            self.register_parameter('bias', None)
        self.reset_parameters()

    def reset_parameters(self):
        stdv = 1. / math.sqrt(self.weight.size(1))
        self.weight.data.uniform_(-stdv, stdv)
        if self.bias is not None:
            self.bias.data.uniform_(-stdv, stdv)

    def forward(self, input, adj):
        support = torch.mm(input, self.weight)
        output = torch.spmm(adj, support)
        if self.bias is not None:
            return output + self.bias
        else:
            return output

    def __repr__(self):
        return self.__class__.__name__ + ' (' \
               + str(self.in_features) + ' -> ' \
               + str(self.out_features) + ')'

2、属性定义

GraphConvolution作为一个类，首先需要定义其相关属性。本文中主要定义了其输入特征in_feature、输出特征out_feature两个输入，以及权重weight和偏移向量bias两个参数，同时调用了其参数初始化的方法（参数初始化此处不做详细说明）。

由于在训练过程中，参数是可以训练的，即可以求其梯度，因此使用parameter的方式定义。

    def __init__(self, in_features, out_features, bias=True):
        super(GraphConvolution, self).__init__()
        self.in_features = in_features
        self.out_features = out_features
        # 由于weight是可以训练的，因此使用parameter定义
        self.weight = Parameter(torch.FloatTensor(in_features, out_features))
        # 由于bias是可以训练的，因此使用parameter定义
        if bias:
            self.bias = Parameter(torch.FloatTensor(out_features))
        else :
            self.register_parameter('bias', None)
        self.reset_parameter()

3、参数初始化

为了让每次训练产生的初始参数尽可能的相同，从而便于实验结果的复现，可以设置固定的随机数生成种子。

    def reset_parameter(self):
        # size()函数主要是用来统计矩阵元素个数，或矩阵某一维上的元素个数的函数  size（1）为行
        stdv = 1. / math.sqrt(self.weight.size(1))
        # uniform() 方法将随机生成下一个实数，它在 [x, y] 范围内
        self.weight.data.uniform_(-stdv, stdv)
        if self.bias is not None:
            self.bias.data.uniform_(-stdv, stdv)

4、前馈计算

此处主要定义的是本层的前向传播，通常采用的是 $A\ast X\ast W$的计算方法。由于A是一个sparse变量，因此其与X进行卷积的结果也是稀疏矩阵。

    def forward(self, input, adj) :
        # torch.mm(a, b)是矩阵a和b矩阵相乘，torch.mul(a, b)是矩阵a和b对应位相乘，a和b的维度必须相等
        # torch.spmm(a,b)是稀疏矩阵相乘
        support = torch.mm(input, self.weight)
        output = torch.spmm(adj, support)
        if self.bias is not None:
            return output + self.bias
        else :
            return output

5、字符串表达

__repr__()方法是类的实例化对象用来做“自我介绍”的方法，默认情况下，它会返回当前对象的“类名+object at+内存地址”， 而如果对该方法进行重写，可以为其制作自定义的自我描述信息。

    def __repr__(self):
        return self.__class__.__name__ + '(' \
               + str(self.in_features) + '->' \
               + str(self.out_features) + ')'

五、train代码分析

train代码主要完成了函数的训练步骤，由于该文件主要完成对上述函数的调用，因此只是在程序中进行详细的注释，不在分函数进行介绍。

# 在 Python2 中导入未来的支持的语言特征中division (精确除法)，
# 即from __future__ import division ，当我们在程序中没有导入该特征时，
# "/“操作符执行的只能是整除，也就是取整数，只有当我们导入division(精确算法)以后，
# ”/"执行的才是精确算法。
from __future__ import division
# 在开头加上from __future__ import print_function这句之后，即使在python2.X，
# 使用print就得像python3.X那样加括号使用。python2.X中print不需要括号，而在python3.X中则需要。
from __future__ import print_function

import sys
import time
import argparse
import numpy as np

import torch
import torch.nn.functional as F
import torch.optim as optim

from utils import load_data, accuracy
from models import GCN

'''
定义一个显示超参数的函数，将代码中所有的超参数打印
'''
def show_Hyperparameter(args):
    argsDict = args.__dict__
    print(argsDict)
    print('the settings are as following')
    for key in argsDict:
        print(key,':',argsDict[key])
'''
训练设置
'''
parser = argparse.ArgumentParser()
parser.add_argument('--no-cuda', action='store_true', default=False,
                    help='Disables CUDA training.')
parser.add_argument('--fastmode',action='store_true', default=False,
                    help='Validate during traing pass')
parser.add_argument('--seed', type=int, default=42, help='Random seed')
parser.add_argument('--epochs', type=int, default=200,
                    help='Number of epochs to train')
parser.add_argument('--lr', type=float, default=0.01,
                    help='Initial learning rate')
# 权重衰减
parser.add_argument('--weight_decay', type=float, default=5e-4,
                    help='Weight decay (L2 loss on parameters)')
parser.add_argument('--hidden', type=int, default=16,
                    help='Number of hidden units')
parser.add_argument('--dropout', type=float, default=0.5,
                    help='Dropout rate (1 - keep probability)')

# 如果程序不禁止使用gpu且当前主机的gpu可用，arg.cuda就为True
args = parser.parse_args()
show_Hyperparameter(args)
args.cuda = not args.no_cuda and torch.cuda.is_available()

# 指定生成随机数的种子，从而每次生成的随机数都是相同的，通过设定随机数种子的好处是，使模型初始化的可学习参数相同，从而使每次的运行结果可以复现。
np.random.seed(args.seed)
if args.cuda:
    torch.cuda.manual_seed(args.seed)
else:
    torch.manual_seed(args.seed)

'''
开始训练
'''

# 载入数据
adj, features, labels, idx_train, idx_val, idx_test = load_data()

# Model and optimizer
model = GCN(nfeat=features.shape[1],
            nhid=args.hidden,
            nclass=labels.max().item() + 1,
            dropout=args.dropout)
optimizer = optim.Adam(model.parameters(),
                       lr=args.lr, weight_decay=args.weight_decay)

# 如果可以使用GPU，数据写入cuda，便于后续加速
# .cuda()会分配到显存里（如果gpu可用）
if args.cuda:
    model.cuda()
    features = features.cuda()
    adj = adj.cuda()
    labels = labels.cuda()
    idx_val = idx_val.cuda()
    idx_test = idx_test.cuda()
    idx_train = idx_train.cuda()


def train(epoch):
    # 返回当前时间
    t = time.time()
    # 将模型转为训练模式，并将优化器梯度置零
    model.train()
    # optimizer.zero_grad()意思是把梯度置零，也就是把loss关于weight的导数变成0.
    # pytorch中每一轮batch需要设置optimizer.zero_grad
    optimizer.zero_grad()
    # 由于在算output时已经使用了log_softmax，这里使用的损失函数就是NLLloss，如果前面没有加log运算，
    # 这里就要使用CrossEntropyLoss了
    # 损失函数NLLLoss() 的输入是一个对数概率向量和一个目标标签. 它不会为我们计算对数概率，
    # 适合最后一层是log_softmax()的网络. 损失函数 CrossEntropyLoss() 与 NLLLoss() 类似,
    # 唯一的不同是它为我们去做 softmax.可以理解为：CrossEntropyLoss()=log_softmax() + NLLLoss()
    # 理论上对于单标签多分类问题，直接经过softmax求出概率分布，然后把这个概率分布用crossentropy做一个似然估计误差。
    # 但是softmax求出来的概率分布，每一个概率都是(0,1)的，这就会导致有些概率过小，导致下溢。 考虑到这个概率分布总归是
    # 要经过crossentropy的，而crossentropy的计算是把概率分布外面套一个-log 来似然，那么直接在计算概率分布的时候加
    # 上log,把概率从（0，1）变为（-∞，0），这样就防止中间会有下溢出。 所以log_softmax说白了就是将本来应该由crossentropy做
    # 的套log的工作提到预测概率分布来，跳过了中间的存储步骤，防止中间数值会有下溢出，使得数据更加稳定。 正是由于把log这一步从计
    # 算误差提到前面，所以用log_softmax之后，下游的计算误差的function就应该变成NLLLoss(它没有套log这一步，直接将输入取反，
    # 然后计算和label的乘积求和平均)

    # 计算输出时，对所有的节点都进行计算
    output = model(features, adj)
    # 损失函数，仅对训练集的节点进行计算，即：优化对训练数据集进行
    loss_train = F.nll_loss(output[idx_train], labels[idx_train])
    # 计算准确率
    acc_train = accuracy(output[idx_train], labels[idx_train])
    # 反向求导  Back Propagation
    loss_train.backward()
    # 更新所有的参数
    optimizer.step()
    # 通过计算训练集损失和反向传播及优化，带标签的label信息就可以smooth到整个图上（label information is smoothed over the graph）。

    # 先是通过model.eval()转为测试模式，之后计算输出，并单独对测试集计算损失函数和准确率。
    if not args.fastmode:
        # Evaluate validation set performance separately,
        # deactivates dropout during validation run.
        # eval() 函数用来执行一个字符串表达式，并返回表达式的值
        model.eval()
        output = model(features, adj)

    # 验证集的损失函数
    loss_val = F.nll_loss(output[idx_val], labels[idx_val])
    acc_val = accuracy(output[idx_val], labels[idx_val])

    print('Epoch: {:04d}'.format(epoch+1),
          'loss_train: {:.4f}'.format(loss_train.item()),
          'acc_train: {:.4f}'.format(acc_train.item()),
          'loss_val: {:.4f}'.format(loss_val.item()),
          'acc_val: {:.4f}'.format(acc_val.item()),
          'time: {:.4f}'.format(time.time() - t))

# 定义测试函数，相当于对已有的模型在测试集上运行对应的loss与accuracy
def test():
    model.eval()
    output = model(features, adj)
    loss_test = F.nll_loss(output[idx_test], labels[idx_test])
    acc_test = accuracy(output[idx_test], labels[idx_test])
    print("Test set results:",
          "loss= {:.4f}".format(loss_test.item()),
          "accuracy= {:.4f}".format(acc_test.item()))

# Train model  逐个epoch进行train，最后test
t_total = time.time()
for epoch in range(args.epochs):
    train(epoch)
print("Optimization Finished!")
print("Total time elapsed: {:.4f}s".format(time.time() - t_total))

test()

torch.cuda.empty_cache()