matlab里BP神经网络实现实例2汽油辛烷值预测
一、引入
1.首先得到数据,比如数据是从exce导入,也可以是现成的.mat文件。60组汽油样品,利用傅里叶近红外变换光谱仪对其进行扫描,扫描范围900~1700nm,扫描间隔2nm,每个样品的光谱曲线共含401个波长点。
2.需要用到的一些函数
归一化函数(mapminmax)
[Y,P] = mapminmax(X,YMIN,YMAX)
YMIN是我们期望归一化后矩阵Y每行的最小值,
YMAX是我们期望归一化后矩阵Y每行的最大值。
Y = mapminmax(‘apply’,X,PS)
PS是训练样本的映射,测试样本的预处理方式应与训练样本相同。只需将映射PS apply到测试样本。;apply运用前一个方法
为什么要归一化?
输入数据的单位不一样,有些数据的范围可能特别大,导致的结果是神经网络收敛慢、训练时间长。
newff (前馈反向传播网络)
net = newff(P,T,S) % 这两种定义都可以
net = newff(P,T,S,TF,BTF,BLF,PF,IPF,OPF,DDF)
P:输入参数矩阵。(RxQ1),其中Q1代表R元的输入向量。其数据意义是矩阵P有Q1列,每一列都是一个样本,而每个样本有R个属性(特征)。一般矩阵P需要归一化,即P的每一行都归一化到[0 1]或者[-1 1]。
T:目标参数矩阵。(SNxQ2),Q2代表SN元的目标向量。
S:N-1个隐含层的数目(S(i)到S(N-1)),默认为空矩阵[]。输出层的单元数目SN取决于T。返回N层的前馈BP神经网络
TF:相关层的传递函数,默认隐含层为tansig函数,输出层为purelin函数。
BTF:BP神经网络学习训练函数,默认值为trainlm函数。
BLF:权重学习函数,默认值为learngdm。
PF:性能函数,默认值为mse,可选择的还有sse,sae,mae,crossentropy。
IPF,OPF,DDF均为默认值即可。
2,传递函数TF
purelin: 线性传递函数。
tansig :正切S型传递函数。
logsig :对数S型传递函数。
隐含层和输出层函数的选择对BP神经网络预测精度有较大影响,一般隐含层节点转移函数选用 tansig函数或logsig函数,输出层节点转移函数选用tansig函数或purelin函数。
3,学习训练函数BTF
traingd:最速下降BP算法。
traingdm:动量BP算法。
trainda:学习率可变的最速下降BP算法。
traindx:学习率可变的动量BP算法。
trainrp:弹性算法。
变梯度算法:
traincgf(Fletcher-Reeves修正算法)
traincgp(Polak_Ribiere修正算法)
traincgb(Powell-Beale复位算法)
trainbfg(BFGS 拟牛顿算法)
trainoss(OSS算法)
4,参数说明
通过net.trainParam可以查看参数
Show Training Window Feedback showWindow: true
Show Command Line Feedback showCommandLine: false
Command Line Frequency show: 两次显示之间的训练次数
Maximum Epochs epochs: 训练次数
Maximum Training Time time: 最长训练时间(秒)
Performance Goal goal: 网络性能目标
Minimum Gradient min_grad: 性能函数最小梯度
Maximum Validation Checks max_fail: 最大验证失败次数
Learning Rate lr: 学习速率
Learning Rate Increase lr_inc: 学习速率增长值
Learning Rate lr_dec: 学习速率下降值
Maximum Performance Increase max_perf_inc:
Momentum Constant mc: 动量因子
二、实例2汽油辛烷值预测
1.问题介绍
背景
辛烷值是汽油最重要的品质指标,传统的实验室检测方法存在样品用量大,测试周期长和费用高等问题,不适用于生产控制,特别是在线测试。近年发展起来的近红外光谱分析方法〈NIR),作为一种快速分析方法,已广泛应用于农业、制药、生物化工、石油产品等领域。其优越性是无损检测、低成本、无污染,能在线分析,更适合于生产和控制的需要。
问题描述
针对采集得到的60组汽油样品,利用傅里吐近红外变换光谱仪对其进行扫描,扫描范围900~1700nm,扫描间隔2nm,每个样品的光谱曲线共含401个波长点孑样品的近红外光谱曲线如图25-3所示。同时,利用传统实验室检测方法测定其辛烷值含量。现要求利用BP及RBF神经网络分别建立汽油样品近红外光谱及其辛烷值间的数学模型,并对模型的性能进行评价。
模型建立
依据问题描述中的要求,实现BEP及RBF神经网络的模型建立及性能评价,大体上可以分为以下几个步骤。
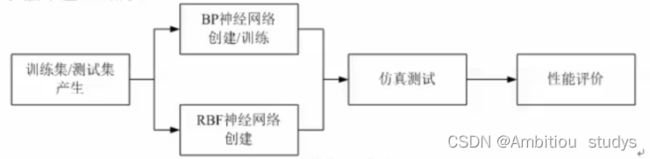
2.matlab代码步骤
%% 清空环境变量
%保存: save( 'filename’, 'net')filename可包含路径,如D:\matlab\.. ..
%调用:load( 'filename ' , 'net')
clear all
clc
%% II. 训练集/测试集产生
% 1.导入数据,60组汽油样品,利用傅里叶近红外变换光谱仪对其进行扫描,扫描范围900~1700nm,扫描间隔2nm,每个样品的光谱曲线共含401个波长点。
load spectra_data.mat
% 2. 随机产生训练集和测试集
%size(a,1)表示显示矩阵的行数,size(a,2)表示显示矩阵的列数
%randperm(60)生成60个乱序排列序列
temp = randperm(size(NIR,1));
% 训练集——50个样本
P_train = NIR(temp(1:50),:)';%取出前50行所有列数据作为训练集输入,转置
T_train = octane(temp(1:50),:)';%取出前50行所有列数据作为训练集输出,转置
% 测试集——10个样本
P_test = NIR(temp(51:end),:)';
T_test = octane(temp(51:end),:)';
N = size(P_test,2);
%% 3.数据归一化
%映射数据到一个合理的取值范围,加快训练速度
[p_train, ps_input] = mapminmax(P_train,0,1);%归一化调用函数mapminmax,归一化数据在0-1之间,且存在p_train矩阵里,归一化的方法存在ps_input
p_test = mapminmax('apply',P_test,ps_input);%apply运用前一个方法把P_test归一化
[t_train, ps_output] = mapminmax(T_train,0,1);
%% 4. BP神经网络创建、训练及仿真测试
% 1. 创建网络
net = newff(p_train,t_train,9);%9个隐藏神经元
% 2. 设置训练参数
net.trainParam.epochs = 1000;%迭代次数
net.trainParam.goal = 1e-3;%停止目标
net.trainParam.lr = 0.01;%学习率
% 3. 训练网络
net = train(net,p_train,t_train);
% 4. 仿真测试,采用测试样本的输入数据进行仿真,测试输出的误差
t_sim = sim(net,p_test);
% 5. 数据反归一化,还原测试数据,与真实数据进行比较
T_sim = mapminmax('reverse',t_sim,ps_output);
%% V. 性能评价
% 1. 相对误差error
error = abs(T_sim - T_test)./T_test;
%%
% 2. 决定系数R^2
R2 = (N * sum(T_sim .* T_test) - sum(T_sim) * sum(T_test))^2 / ((N * sum((T_sim).^2) - (sum(T_sim))^2) * (N * sum((T_test).^2) - (sum(T_test))^2));
%%
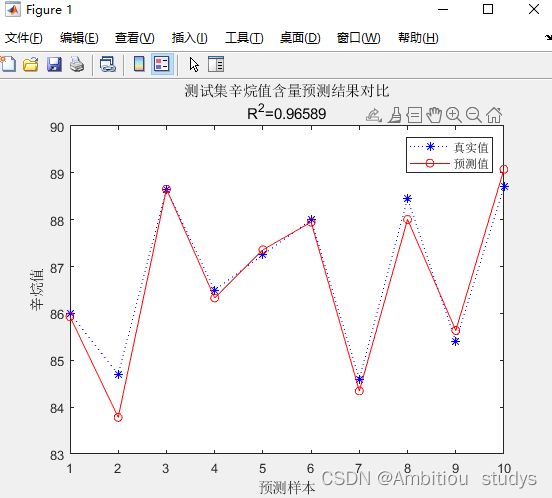
% 3. 结果对比
result = [T_test' T_sim' error']
%% VI. 绘图
figure
plot(1:N,T_test,'b:*',1:N,T_sim,'r-o')
legend('真实值','预测值')
xlabel('预测样本')
ylabel('辛烷值')
string = {'测试集辛烷值含量预测结果对比';['R^2=' num2str(R2)]};
title(string)
重新训练一次
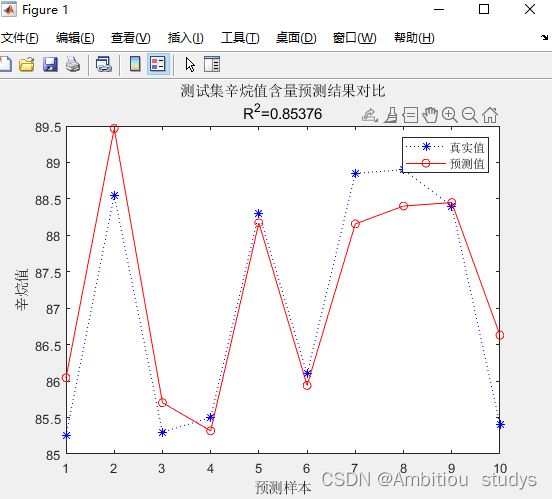
后面根据自己的神经元个数或者隐藏层数或者训练优化算法修改
表达方式1:
net=newff([T,C,{'tansig','purelin'},'traingd');
%net = newff(T,C,[隐层的神经元的个数,输出层的神经元的个数],{隐层神经元的传输函数,输出层的传输函数},‘反向传播的训练函数’),其中p为输入数据,t为输出数据
%神经网络的传输函数,默认为’tansig’函数为隐层的传输函数
%purelin函数为输出层的传输函数,如下还有
%TF1 = ‘tansig’;TF2 = ‘logsig’;
%TF1 = ‘logsig’;TF2 = ‘purelin’;
%TF1 = ‘logsig’;TF2 = ‘logsig’;
%TF1 = ‘purelin’;TF2 = ‘purelin’;
TF1 = ‘tansig’;TF2 = ‘purelin’;
表达方式2:
net=newff(T,C,{TF1 TF2},'traingdm');%网络创建
%net.trainParam.epochs=10000;%训练次数设置
%net.trainParam.goal=1e-7;%训练目标设置
%net.trainParam.lr=0.01;%学习率设置,应设置为较少值,太大虽然会在开始加快收敛速度,但临近最佳点时,会产生动荡,而致使无法收敛
%net.trainParam.mc=0.9;%动量因子的设置,默认为0.9
%net.trainParam.show=25;%显示的间隔次数
%%
net.trainFcn = 'traingd'; % 梯度下降算法
net.trainFcn = 'traingdm'; % 动量梯度下降算法
net.trainFcn = 'traingda'; % 变学习率梯度下降算法
net.trainFcn = 'traingdx'; % 变学习率动量梯度下降算法
% (大型网络的首选算法)
net.trainFcn = 'trainrp'; % RPROP(弹性BP)算法,内存需求最小
% 共轭梯度算法
net.trainFcn = 'traincgf'; %Fletcher-Reeves修正算法
net.trainFcn = 'traincgp'; %Polak-Ribiere修正算法,内存需求比Fletcher-Reeves修正算法略大
net.trainFcn = 'traincgb'; % Powell-Beal复位算法,内存需求比Polak-Ribiere修正算法略大
% (大型网络的首选算法)
net.trainFcn = 'trainscg'; % ScaledConjugate Gradient算法,内存需求与Fletcher-Reeves修正算法相同,计算量比上面三种算法都小很多
net.trainFcn = 'trainbfg'; %Quasi-Newton Algorithms - BFGS Algorithm,计算量和内存需求均比共轭梯度算法大,但收敛比较快
net.trainFcn = 'trainoss'; % OneStep Secant Algorithm,计算量和内存需求均比BFGS算法小,比共轭梯度算法略大
% (中型网络的首选算法)
net.trainFcn = 'trainlm'; %Levenberg-Marquardt算法,内存需求最大,收敛速度最快
net.trainFcn = 'trainbr'; % 贝叶斯正则化算法
有代表性的五种算法为:'traingdx','trainrp','trainscg','trainoss', 'trainlm'
%在这里一般是选取'trainlm'函数来训练,其算对对应的是Levenberg-Marquardt算法