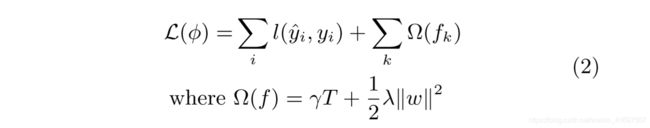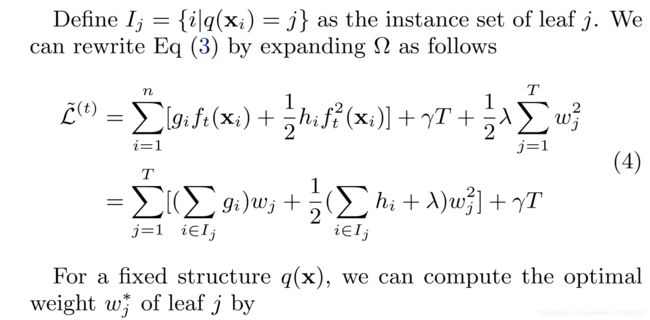XGBoost: A Scalable Tree Boosting System（XGBoost：一个可扩展的树提升系统）

XGBoost: A Scalable Tree Boosting System

ABSTRACT

Tree boosting is a highly e ective and widely used machine learning method. In this paper, we describe a scalable end-to-end tree boosting system called XGBoost, which is used widely by data scientists to achieve state-of-the-art results on many machine learning challenges. We propose a novel sparsity-aware algorithm for sparse data and weighted quan-tile sketch for approximate tree learning. More importantly, we provide insights on cache access patterns, data compres-sion and sharding to build a scalable tree boosting system. By combining these insights, XGBoost scales beyond billions of examples using far fewer resources than existing systems.
树推进是一种高效且广泛使用的机器学习方法。 在本文中，我们描述了一个可扩展的端到端树推进系统XGBoost，它被数据科学家广泛使用，以在许多机器学习挑战中获得最先进的结果。 我们提出了一种新的稀疏数据稀疏感知算法和近似树学习的加权量化草图。 更重要的是，我们提供有关缓存访问模式，数据压缩和分片的见解，以构建可扩展的树提升系统。 通过结合这些见解，XGBoost使用比现有系统少得多的资源来扩展数十亿个示例。

Keywords

Large-scale Machine Learning

1.INTRODUCTION

Machine learning and data-driven approaches are becoming very important in many areas. Smart spam classi ers protect our email by learning from massive amounts of spam data and user feedback; advertising systems learn to match the right ads with the right context; fraud detection systems protect banks from malicious attackers; anomaly event detection systems help experimental physicists to nd events that lead to new physics. There are two important factors that drive these successful applications: usage of e ective (statistical) models that capture the complex data dependencies and scalable learning systems that learn the model of interest from large datasets.
机器学习和数据驱动方法在许多领域都非常重要。 智能垃圾邮件分类器通过学习大量的spam数据和用户反馈来保护我们的电子邮件; 广告系统学会将正确的广告与正确的背景相匹配; 欺诈检测系统保护银行免受恶意攻击者的侵害 异常事件检测系统帮助实验物理学家找到导致新物理学的事件。 驱动这些成功应用程序有两个重要因素：使用捕获复杂数据依赖关系的有效（统计）模型和可从大型数据集中学习感兴趣模型的可扩展学习系统。

Among the machine learning methods used in practice, gradient tree boosting [10]1 is one technique that shines in many applications. Tree boosting has been shown to give state-of-the-art results on many standard classification benchmarks [16]. LambdaMART [5], a variant of tree boost-ing for ranking, achieves state-of-the-art result for ranking problems. Besides being used as a stand-alone predictor, it is also incorporated into real-world production pipelines for ad click through rate prediction [15]. Finally, it is the de-facto choice of ensemble method and is used in challenges such as the Netix prize [3].

在实践中使用的机器学习方法中，梯度树增强[10] 1是一种在许多应用中闪耀的技术。 树木增强已被证明可以在许多标准分类基准上给出最先进的结果[16]。 LambdaMART [5]是用于排名的树推进的变体，它实现了排名问题的最新结果。 除了用作独立预测器之外，它还被整合到实际生产流水线中，用于广告点击率预测[15]。 最后，它是集合方法的事实上的选择，并用于Netix奖[3]等挑战。

In this paper, we describe XGBoost, a scalable machine learning system for tree boosting. The system is available as an open source package2. The impact of the system has been widely recognized in a number of machine learning and data mining challenges. Take the challenges hosted by the machine learning competition site Kaggle for example. A-mong the 29 challenge winning solutions 3 published at Kag-gle’s blog during 2015, 17 solutions used XGBoost. Among these solutions, eight solely used XGBoost to train the mod-el, while most others combined XGBoost with neural net-s in ensembles. For comparison, the second most popular method, deep neural nets, was used in 11 solutions. The success of the system was also witnessed in KDDCup 2015, where XGBoost was used by every winning team in the top-10. Moreover, the winning teams reported that ensemble methods outperform a well-con gured XGBoost by only a small amount [1].

在本文中，我们描述了XGBoost，一种用于树木提升的可扩展机器学习系统。 该系统可作为开源软件包2使用。 该系统的影响已在许多机器学习和数据挖掘挑战中得到广泛认可。 以机器学习竞赛网站Kaggle主持的挑战为例。 A-mong在2015年Kag-gle的博客上发布了29个挑战获胜解决方案，17个解决方案使用了XGBoost。 在这些解决方案中，八个仅使用XGBoost来训练模型，而大多数其他解决方案将XGBoost与神经网络结合在一起。 为了比较，第二种最常用的方法是深度神经网络，用于11种解决方案。 该系统的成功也在KDDCup 2015中见证，其中XGBoost被前10名中的每个获胜团队使用。 此外，获胜团队报告说，整体方法仅仅在很少量的情况下胜过良好的XGBoost [1]。

These results demonstrate that our system gives state-of-the-art results on a wide range of problems. Examples of the problems in these winning solutions include: store sales prediction; high energy physics event classi cation; web text classi cation; customer behavior prediction; motion detec-tion; ad click through rate prediction; malware classi cation; product categorization; hazard risk prediction; massive on-line course dropout rate prediction. While domain depen-dent data analysis and feature engineering play an important role in these solutions, the fact that XGBoost is the consen-sus choice of learner shows the impact and importance of our system and tree boosting.

这些结果表明，我们的系统在广泛的问题上提供了最先进的结果。 这些获胜解决方案中存在的问题包括：商店销售预测; 高能物理事件分类; 网络文本分类; 顾客行为预测; 运动检测; 广告点击率预测; 恶意软件分类; 产品分类; 危险风险预测; 大规模的在线课程辍学率预测。 虽然域依赖数据分析和特征工程在这些解决方案中发挥着重要作用，但XGBoost是学习者的共识选择这一事实表明了我们的系统和树提升的影响和重要性。

The most important factor behind the success of XGBoost is its scalability in all scenarios. The system runs more than ten times faster than existing popular solutions on a single machine and scales to billions of examples in distributed or memory-limited settings. The scalability of XGBoost is due to several important systems and algorithmic optimizations. These innovations include: a novel tree learning algorithm is for handling sparse data; a theoretically justi ed weighted quantile sketch procedure enables handling instance weights in approximate tree learning. Parallel and distributed com-puting makes learning faster which enables quicker model ex-ploration. More importantly, XGBoost exploits out-of-core computation and enables data scientists to process hundred millions of examples on a desktop. Finally, it is even more exciting to combine these techniques to make an end-to-end system that scales to even larger data with the least amount of cluster resources. The major contributions of this paper is listed as follows:

XGBoost成功背后最重要的因素是它在所有场景中的可扩展性。该系统在单台机器上运行速度比现有流行解决方案快十倍以上，并且可以在分布式或内存限制设置中扩展到数十亿个示例。 XGBoost的可扩展性归功于几个重要的系统和算法优化。这些创新包括：一种新颖的树学习算法，用于处理稀疏数据;理论上加权的加权分位数草图程序使得能够在近似树学习中处理实例权重。并行和分布式计算使学习更快，从而可以更快地进行模型探索。更重要的是，XGBoost利用核外计算，使数据科学家能够在桌面上处理数亿个示例。最后，结合这些技术使端到端系统以最少的集群资源扩展到更大的数据更令人兴奋。本文的主要贡献如下：

We design and build a highly scalable end-to-end tree boosting system.

We propose a theoretically justi ed weighted quantile sketch for e cient proposal calculation.

We introduce a novel sparsity-aware algorithm for par-allel tree learning.

We propose an e ective cache-aware block structure for out-of-core tree learning.

While there are some existing works on parallel tree boost-ing [22, 23, 19], the directions such as out-of-core compu-tation, cache-aware and sparsity-aware learning have not been explored. More importantly, an end-to-end system that combines all of these aspects gives a novel solution for real-world use-cases. This enables data scientists as well as researchers to build powerful variants of tree boosting al-gorithms [7, 8]. Besides these major contributions, we also make additional improvements in proposing a regularized learning objective, which we will include for completeness.

The remainder of the paper is organized as follows. We will rst review tree boosting and introduce a regularized objective in Sec. 2. We then describe the split nding meth-ods in Sec. 3 as well as the system design in Sec. 4, including experimental results when relevant to provide quantitative support for each optimization we describe. Related work is discussed in Sec. 5. Detailed end-to-end evaluations are included in Sec. 6. Finally we conclude the paper in Sec. 7.

我们设计并构建了一个高度可扩展的端到端树推进系统。

我们提出了一个理论上合理的加权分位数草图，用于有效的提议计算。

我们为par-allel树学习引入了一种新颖的稀疏感知算法。

我们提出了一种用于核外树学习的有效缓存感知块结构。

虽然现有一些关于并行树增强的工作[22,23,19]，但尚未探索诸如核外计算，高速缓存感知和稀疏感知学习等方向。更重要的是，结合所有这些方面的端到端系统为现实世界的用例提供了一种新颖的解决方案。这使数据科学家和研究人员能够构建树木增强算法的强大变体[7,8]。除了这些主要贡献之外，我们还在提出正规化学习目标方面做出了进一步的改进，我们将包括完整性。

在本文的其余部分安排如下。我们将首先回顾树的推进并在Sec中引入正则化的目标。然后我们描述了Sec中的分裂方法。 3以及Sec中的系统设计。 4，包括相关的实验结果，为我们描述的每个优化提供定量支持。相关工作在第二节中讨论。 5.详细的端到端评估包含在Sec。最后，我们在第二节总结了这篇论文。 7。

TREE BOOSTING IN A NUTSHELL

We review gradient tree boosting algorithms in this sec-tion. The derivation follows from the same idea in existing literatures in gradient boosting. Specicially the second order method is originated from Friedman et al. [12]. We make mi-nor improvements in the reguralized objective, which were found helpful in practice.

我们将在本节中回顾渐变树增强算法。 推导遵循现有文献中梯度增强的相同思想。 特别地，二阶方法源自Friedman等人。[12]。 我们对法律化的目标进行了微观改进，这在实践中是有帮助的。

2.1 Regularized Learning Objective

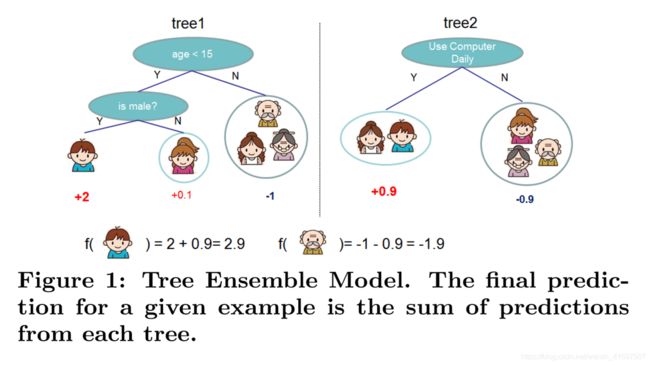
图1：树集合模型。 给定示例的最终预测是每棵树的预测总和。

它进入叶子并通过总结相应叶子中的分数（由w给出）来计算最终预测。 要了解模型中使用的函数集，我们最小化以下正则化目标。

Here l is a di erentiable convex loss function that measures the di erence between the prediction y^i and the target yi. The second term penalizes the complexity of the model (i.e., the regression tree functions). The additional regular-ization term helps to smooth the nal learnt weights to avoid over- tting. Intuitively, the regularized objective will tend to select a model employing simple and predictive functions. A similar regularization technique has been used in Regu-larized greedy forest (RGF) [25] model. Our objective and the corresponding learning algorithm is simpler than RGF and easier to parallelize. When the regularization parame-ter is set to zero, the objective falls back to the traditional gradient tree boosting.

这里l是一个不可靠的凸损失函数，它测量预测y ^ i和目标yi之间的差异。 第二项惩罚模型的复杂性（即回归树函数）。 额外的规则化术语有助于平滑最终学习的权重，以避免过度。 直观地，正则化目标将倾向于选择采用简单和预测函数的模型。 类似的正则化技术已被用于Regu-larized贪婪林（RGF）[25]模型。 我们的目标和相应的学习算法比RGF更简单，更易于并行化。 当正则化参数设置为零时，目标回退到传统的梯度树提升。

2.2 Gradient Tree Boosting

图2：结构分数计算。 我们只需要总结每个叶子上的梯度和二阶梯度统计量，然后应用得分公式来获得质量得分。

Eq (6) can be used as a scoring function to measure the quality of a tree structure q. This score is like the impurity score for evaluating decision trees, except that it is derived for a wider range of objective functions. Fig. 2 illustrates how this score can be calculated.
方程（6）可以用作评分函数来测量树结构q的质量。 该评分类似于评估决策树的杂质评分，除了它是针对更广泛的目标函数得出的。 图2说明了如何计算得分。

This formula is usually used in practice for evaluating the split candidates.

2.3 Shrinkage and Column Subsampling

Besides the regularized objective mentioned in Sec. 2.1, two additional techniques are used to further prevent over-tting. The rst technique is shrinkage introduced by Fried-man [11]. Shrinkage scales newly added weights by a factor n after each step of tree boosting. Similar to a learning rate in tochastic optimization, shrinkage reduces the inuence of each individual tree and leaves space for future trees and leaves space for future trees to improve the model. The second technique is column (feature) subsampling. This technique is used in RandomForest [4, 13], It is implemented in a commercial software TreeNet 4

(6)for gradient boosting, but is not implemented in existing opensource packages. According to user feedback, using col-umn sub-sampling prevents over- tting even more so than the traditional row sub-sampling (which is also supported). The usage of column sub-samples also speeds up computa-tions of the parallel algorithm described later.

除了第二节中提到的正则化目标。 2.1，使用另外两种技术来进一步防止过度使用。 第一种技术是Fried-man引入的收缩[11]。 在树木提升的每个步骤之后，收缩比例新增加了因子n的权重。 与随机优化中的学习速率类似，收缩减少了每棵树的影响，为未来的树木留下了空间，为未来的树木留出了改进模型的空间。 第二种技术是列（特征）子采样。 这种技术用于RandomForest [4,13]，它是在商业软件TreeNet 4中实现的

（6）用于梯度增强，但未在现有的开源软件包中实现。 根据用户反馈，使用柱子采样比传统的行子采样（也支持）更能防止过度采样。 列子样本的使用也加速了后面描述的并行算法的计算。

3. SPLIT FINDING ALGORITHMS

3.1 Basic Exact Greedy Algorithm

One of the key problems in tree learning is to nd the best split as indicated by Eq (7). In order to do so, a s-plit nding algorithm enumerates over all the possible splits on all the features. We call this the exact greedy algorithm. Most existing single machine tree boosting implementation-s, such as scikit-learn [20], R’s gbm [21] as well as the single machine version of XGBoost support the exact greedy algo-rithm. The exact greedy algorithm is shown in Alg. 1. It is computationally demanding to enumerate all the possible splits for continuous features. In order to do so e ciently, the algorithm must rst sort the data according to feature values and visit the data in sorted order to accumulate the gradient statistics for the structure score in Eq (7).

树学习中的关键问题之一是找到方程（7）所示的最佳分裂。 为此，s-plit nding算法枚举所有特征上的所有可能分裂。 我们称之为精确的贪婪算法。 大多数现有的单机树提升实现，如scikit-learn [20]，R的gbm [21]以及XGBoost的单机版本都支持精确的贪婪算法。 确切的贪婪算法如Alg所示。 1.枚举连续特征的所有可能分裂在计算上要求很高。 为了有效地执行此操作，算法必须首先根据特征值对数据进行排序，并按排序顺序访问数据，以累积方程（7）中结构分数的梯度统计。

3.2 Approximate Algorithm

The exact greedy algorithm is very powerful since it enu-merates over all possible splitting points greedily. However, it is impossible to e ciently do so when the data does not t entirely into memory. Same problem also arises in the dis-tributed setting. To support e ective gradient tree boosting in these two settings, an approximate algorithm is needed.

We summarize an approximate framework, which resem-bles the ideas proposed in past literatures [17, 2, 22], in Alg. 2. To summarize, the algorithm rst proposes candi-date splitting points according to percentiles of feature dis-tribution (a speci c criteria will be given in Sec. 3.3). The algorithm then maps the continuous features into bucket-s split by these candidate points, aggregates the statistics and nds the best solution among proposals based on the aggregated statistics.

确切的贪婪算法非常强大，因为它贪婪地计算所有可能的分裂点。 但是，当数据不完全进入内存时，不可能有效地这样做。 在分布式设置中也会出现同样的问题。 为了支持这两种设置中的有效梯度树增强，需要一种近似算法。

我们总结了一个近似的框架，它类似于过去的文献[17,2,22]中提出的观点，在Alg中。 2.总之，算法首先根据特征分布的百分位数提出了候选分裂点（具体标准将在3.3节中给出）。 然后，算法将连续特征映射到由这些候选点划分的桶中，汇总统计数据并根据聚合统计数据找出提案中的最佳解决方案。

There are two variants of the algorithm, depending on when the proposal is given. The global variant proposes all the candidate splits during the initial phase of tree construction, and uses the same proposals for split nding at all levels.The local variant re-proposes after each split. The global method requires less proposal steps than the local method. However, usually more candidate points are needed for the global proposal because candidates are not re ned after each split. The local proposal re nes the candidates after splits, and can potentially be more appropriate for deeper trees. A comparison of di erent algorithms on a Higgs boson dataset is given by Fig. 3. We nd that the local proposal indeed requires fewer candidates. The global proposal can be as accurate as the local one given enough candidates.

Most existing approximate algorithms for distributed tree learning also follow this framework. Notably, it is also possi-ble to directly construct approximate histograms of gradient statistics [22]. It is also possible to use other variants of bin-ning strategies instead of quantile [17]. Quantile strategy bene t from being distributable and recomputable, which we will detail in next subsection. From Fig. 3, we also nd that the quantile strategy can get the same accuracy as exact greedy given reasonable approximation level.

Our system e ciently supports exact greedy for the single machine setting, as well as approximate algorithm with both local and global proposal methods for all settings. Users can freely choose between the methods according to their needs.

该算法有两种变体，具体取决于提议的时间。全局变体在树构建的初始阶段提出所有候选分裂，并且在所有级别使用相同的分裂结构提议。在每次分割之后重新提出本地变体。全局方法比本地方法需要更少的提议步骤。但是，全球提案通常需要更多候选点，因为在每次拆分后都不会考虑候选人。本地提案在拆分后重新确定候选人，并且可能更适合更深层的树木。图3给出了希格斯玻色子数据集上不同算法的比较。我们认为本地提案确实需要较少的候选者。全球提案可以与给予足够候选人的当地提案一样准确。

用于分布式树学习的大多数现有近似算法也遵循该框架。值得注意的是，直接构建梯度统计的近似直方图也是可能的[22]。也可以使用其他变化的bin-ning策略而不是分位数[17]。分位数和可重组的分位数策略有所好处，我们将在下一小节中详细介绍。从图3中，我们还发现，在给定合理的近似水平的情况下，分位数策略可以获得与精确贪婪相同的精度。

我们的系统有效地支持单机设置的精确贪婪，以及所有设置的本地和全局提议方法的近似算法。用户可以根据自己的需要自由选择方法。

3.3 Weighted Quantile Sketch

One important step in the approximate algorithm is to propose candidate split points. Usually percentiles of a fea-ture are used to make candidates distribute evenly on the data. Formally, let multi-set Dk = f(x1k; h1); (x2k; h2) (xnk; hn)g represent the k-th feature values and second order gradient statistics of each training instances. We can de ne a rank functions rk : R ! [0; +1) as

近似算法中的一个重要步骤是提出候选分裂点。 通常使用特征的百分位来使候选者均匀地分布在数据上。 形式上，让多组Dk = f（x1k; h1）; （x2k; h2）（xnk; hn）g表示每个训练实例的第k个特征值和二阶梯度统计。 我们可以定义一个等级函数rk：R！[0; +1）as

which is exactly weighted squared loss with labels gi=hi and weights hi. For large datasets, it is non-trivial to nd can-didate splits that satisfy the criteria. When every instance has equal weights, an existing algorithm called quantile s-ketch [14, 24] solves the problem. However, there is no existing quantile sketch for the weighted datasets. There-fore, most existing approximate algorithms either resorted to sorting on a random subset of data which have a chance of failure or heuristics that do not have theoretical guarantee.

To solve this problem, we introduced a novel distributed weighted quantile sketch algorithm that can handle weighted data with a provable theoretical guarantee. The general idea is to propose a data structure that supports merge and prune operations, with each operation proven to maintain a certain accuracy level. A detailed description of the algorithm as well as proofs are given in the supplementary material5(link in the footnote).

这是标签gi = hi和权重hi的加权平方损失。 对于大型数据集，满足条件的nd can-didate拆分是非常重要的。 当每个实例具有相等的权重时，称为分位数s-ketch [14,24]的现有算法解决了该问题。 但是，加权数据集不存在现有的分位数草图。 因此，大多数现有的近似算法要么对有可能失败的随机数据子集进行排序，要么使用没有理论保证的启发式算法。

为了解决这个问题，我们引入了一种新颖的分布式加权分位数草图算法，该算法可以处理加权数据并具有可证明的理论保证 一般的想法是提出一种支持合并和修剪操作的数据结构，每个操作都被证明可以保持一定的准确度。 补充材料5（脚注中的链接）给出了算法的详细描述以及证明。

3.4 Sparsity-aware Split Finding

In many real-world problems, it is quite common for the input x to be sparse. There are multiple possible causes for sparsity: 1) presence of missing values in the data; 2) frequent zero entries in the statistics; and, 3) artifacts of feature engineering such as one-hot encoding. It is important to make the algorithm aware of the sparsity pattern in the data. In order to do so, we propose to add a default direction in each tree node, which is shown in Fig. 4. When a value is missing in the sparse matrix x, the instance is classified into the default direction. There are two choices of default direction in each branch. The optimal default directions are learnt from the data. The algorithm is shown in Alg. 3. The key improvement is to only visit the non-missing entries Ik. The presented algorithm treats the non-presence as a missing value and learns the best direction to handle missing values. The same algorithm can also be applied when the non-presence corresponds to a user speci ed value by limiting the enumeration only to consistent solutions.

To the best of our knowledge, most existing tree learning algorithms are either only optimized for dense data, or need speci c procedures to handle limited cases such as categorical encoding. XGBoost handles all sparsity patterns in a uni ed way. More importantly, our method exploits the sparsity to make computation complexity linear to number of non-missing entries in the input. Fig. 5 shows the comparison of sparsity aware and a naive implementation on an Allstate-10K dataset (description of dataset given in Sec. 6). We find that the sparsity aware algorithm runs 50 times faster than the naive version. This confirms the importance of the sparsity aware algorithm.

在许多现实问题中，输入x稀疏是很常见的。稀疏性有多种可能的原因：1）数据中存在缺失值; 2）统计中频繁的零项; 3）特征工程的工件，例如单热编码。使算法了解数据中的稀疏模式非常重要。为此，我们建议在每个树节点中添加一个默认方向，如图4所示。当稀疏矩阵x中缺少一个值时，该实例被分类为默认方向。每个分支中有两种默认方向选择。从数据中学习最佳默认方向。算法显示在Alg中。 3.关键的改进是只访问非缺失的条目Ik。所提出的算法将非存在视为缺失值并且学习处理缺失值的最佳方向。当非存在对应于用户指定的值时，也可以通过将枚举限制为一致的解决方案来应用相同的算法。

据我们所知，大多数现有的树学习算法要么仅针对密集数据进行优化，要么需要特定的过程来处理有限的情况，例如分类编码。 XGBoost以统一的方式处理所有稀疏模式。更重要的是，我们的方法利用稀疏性使计算复杂度与输入中的非缺失条目的数量成线性关系。图5显示了对Allstate-10K数据集的稀疏性和初始实现的比较（第6节中给出的数据集的描述）。我们发现稀疏感知算法比天真版本快50倍。这证实了稀疏感知算法的重要性。

4. SYSTEM DESIGN

4.1 Column Block for Parallel Learning

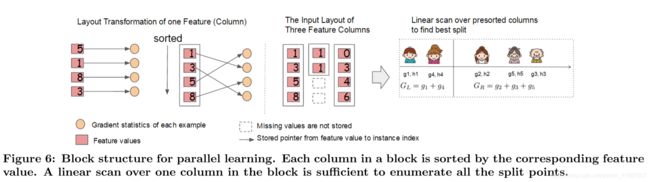
The most time consuming part of tree learning is to get the data into sorted order. In order to reduce the cost of sorting, we propose to store the data in in-memory units, which we called block. Data in each block is stored in the compressed column (CSC) format, with each column sorted by the corresponding feature value. This input data layout only needs to be computed once before training, and can be reused in later iterations.

In the exact greedy algorithm, we store the entire dataset in a single block and run the split search algorithm by lin-early scanning over the presorted entries. We do the split nding of all leaves collectively, so one scan over the block will collect the statistics of the split candidates in all leaf branches. Fig. 6 shows how we transform a dataset into the format and nd the optimal split using the block structure.

The block structure also helps when using the approximate algorithms. Multiple blocks can be used in this case, with each block corresponding to subset of rows in the dataset. Different blocks can be distributed across machines, or stored on disk in the out-of-core setting. Using the sorted structure, the quantile finding step becomes a linear scan over the sorted columns. This is especially valuable for lo-cal proposal algorithms, where candidates are generated frequently at each branch. The binary search in histogram aggregation also becomes a linear time merge style algorithm. Collecting statistics for each column can be parallelized, giving us a parallel algorithm for split finding. Importantly, the column block structure also supports column subsampling, as it is easy to select a subset of columns in a block.

树学习中最耗时的部分是将数据按顺序排列。为了降低排序成本，我们建议将数据存储在内存单元中，我们称之为块。每个块中的数据以压缩列（CSC）格式存储，每列按相应的特征值排序。此输入数据布局仅需要在训练之前计算一次，并且可以在以后的迭代中重复使用。

在精确的贪婪算法中，我们将整个数据集存储在一个块中，并通过对预先排序的条目进行lin-early扫描来运行拆分搜索算法。我们共同对所有叶子进行分割，因此对块进行一次扫描将收集所有叶子分支中的分割候选者的统计数据。图6显示了我们如何使用块结构将数据集转换为格式并找到最佳分割。

在使用近似算法时，块结构也有帮助。在这种情况下可以使用多个块，每个块对应于数据集中的行的子集。不同的块可以跨机器分布，也可以在核外设置中存储在磁盘上。使用排序结构，分位数查找步骤变为对排序列的线性扫描。这对于本地提议算法特别有价值，其中候选者在每个分支处经常生成。直方图聚合中的二分搜索也变为线性时间合并样式算法。收集每列的统计数据可以并行化，为我们提供了一种用于拆分查找的并行算法。重要的是，列块结构还支持列子采样，因为很容易在块中选择列的子集。

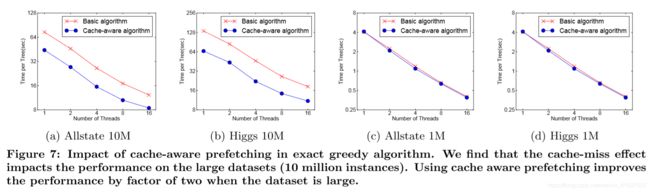
图7：精确贪婪算法中缓存感知预取的影响。 我们发现缓存缺失效应会影响大型数据集（1000万个实例）的性能。 当数据集很大时，使用缓存感知预取可将性能提高两倍。

图8：短距离数据依赖模式，可能由于缓存未命中而导致停顿。

图9：块大小在近似算法中的影响。 我们发现过于小的块会导致无效的并行化，而过大的块也会因缓存未命中而减慢训练速度。

Time Complexity Analysis

4.2 Cache-aware Access

While the proposed block structure helps optimize the computation complexity of split nding, the new algorithm requires indirect fetches of gradient statistics by row index, since these values are accessed in order of feature. This is a non-continuous memory access. A naive implementation of split enumeration introduces immediate read/write de-pendency between the accumulation and the non-continuous memory fetch operation (see Fig. 8). This slows down split nding when the gradient statistics do not t into CPU cache and cache miss occur.

For the exact greedy algorithm, we can alleviate the prob-lem by a cache-aware prefetching algorithm. Speci cally, we allocate an internal bu er in each thread, fetch the gra-dient statistics into it, and then perform accumulation in a mini-batch manner. This prefetching changes the direct read/write dependency to a longer dependency and helps to reduce the runtime overhead when number of rows in the is large. Figure 7 gives the comparison of cache-aware vs. non cache-aware algorithm on the the Higgs and the All-state dataset. We nd that cache-aware implementation of the exact greedy algorithm runs twice as fast as the naive version when the dataset is large.

For approximate algorithms, we solve the problem by choos-ing a correct block size. We de ne the block size to be max-imum number of examples in contained in a block, as this reects the cache storage cost of gradient statistics. Choos-ing an overly small block size results in small workload for each thread and leads to ine cient parallelization. On the other hand, overly large blocks result in cache misses, as the gradient statistics do not t into the CPU cache. A good choice of block size balances these two factors. We compared various choices of block size on two data sets. The results are given in Fig. 9. This result validates our discussion and shows that choosing 216 examples per block balances the cache property and parallelization.

虽然所提出的块结构有助于优化分割中的计算复杂度，但是新算法需要通过行索引间接提取梯度统计，因为这些值是按特征的顺序访问的。这是一种非连续的内存访问。分裂枚举的简单实现引入了累积和非连续存储器获取操作之间的立即读/写依赖性（参见图8）。当梯度统计信息不进入CPU缓存并发生缓存未命中时，这会降低分割速度。

对于精确的贪婪算法，我们可以通过缓存感知预取算法来缓解问题。具体来说，我们在每个线程中分配一个内部缓冲区，获取其中的梯度统计信息，然后以小批量方式执行累积。此预取将直接读/写依赖关系更改为更长的依赖关系，并有助于在其中的行数较大时减少运行时开销。图7给出了Higgs和All-state数据集上缓存感知与非缓存感知算法的比较。我们发现，当数据集很大时，精确贪婪算法的缓存感知实现的运行速度是天真版本的两倍。

对于近似算法，我们通过选择正确的块大小来解决问题。我们将块大小定义为块中包含的最大数量的示例，因为这反映了梯度统计的高速缓存存储成本。选择过小的块大小会导致每个线程的工作量很小，并导致无效的并行化。另一方面，过大的块会导致高速缓存未命中，因为梯度统计信息不会进入CPU高速缓存。块大小的良好选择平衡了这两个因素。我们在两个数据集上比较了块大小的各种选择。结果如图9所示。该结果验证了我们的讨论，并表明每个块选择216个示例可以平衡缓存属性和并行化。

4.3 Blocks for Out-of-core Computation

One goal of our system is to fully utilize a machine’s re-sources to achieve scalable learning. Besides processors and memory, it is important to utilize disk space to handle data that does not t into main memory. To enable out-of-core computation, we divide the data into multiple blocks and store each block on disk. During computation, it is impor-tant to use an independent thread to pre-fetch the block into a main memory bu er, so computation can happen in con-currence with disk reading. However, this does not entirely solve the problem since the disk reading takes most of the computation time. It is important to reduce the overhead and increase the throughput of disk IO. We mainly use two techniques to improve the out-of-core computation.

Block Compression The rst technique we use is block compression. The block is compressed by columns, and de-compressed on the y by an independent thread when load-ing into main memory. This helps to trade some of the computation in decompression with the disk reading cost. We use a general purpose compression algorithm for com-pressing the features values. For the row index, we substract the row index by the begining index of the block and use a 16bit integer to store each o set. This requires 216 examples per block, which is con rmed to be a good setting. In most of the dataset we tested, we achieve roughly a 26% to 29% compression ratio.

Block Sharding The second technique is to shard the data onto multiple disks in an alternative manner. A pre-fetcher thread is assigned to each disk and fetches the data into an in-memory bu er. The training thread then alternatively reads the data from each bu er. This helps to increase the throughput of disk reading when multiple disks are available.

我们系统的一个目标是充分利用机器的资源来实现可扩展的学习。除了处理器和内存之外，利用磁盘空间来处理不会进入主内存的数据也很重要。为了实现核外计算，我们将数据分成多个块并将每个块存储在磁盘上。在计算过程中，使用独立的线程将块预取到主存储器中是很重要的，因此计算可以在与磁盘读取相关的情况下发生。但是，这并不能完全解决问题，因为磁盘读取占用了大部分计算时间。减少开销并增加磁盘IO的吞吐量非常重要。我们主要使用两种技术来改进核外计算。

块压缩我们使用的第一种技术是块压缩。该块由列压缩，并在加载到主存储器时由独立线程在y上解压缩。这有助于将解压缩中的一些计算与磁盘读取成本进行交换。我们使用通用压缩算法来压缩特征值。对于行索引，我们通过块的开始索引来减去行索引，并使用16位整数来存储每个o set。这需要每个块216个示例，这被认为是一个很好的设置。在我们测试的大多数数据集中，我们实现了大约26％到29％的压缩比。

块分片第二种技术是以另一种方式将数据分片到多个磁盘上。为每个磁盘分配一个预取线程，并将数据提取到内存中。然后，训练线程交替地从每个存储器读取数据。当有多个磁盘可用时，这有助于提高磁盘读取的吞吐量。

5.RELATED WORKS

Our system implements gradient boosting [10], which per-forms additive optimization in functional space. Gradient tree boosting has been successfully used in classi cation [12], learning to rank [5], structured prediction [8] as well as other elds. XGBoost incorporates a regularized model to prevent overfitting. This this resembles previous work on regularized greedy forest [25], but simpli es the objective and algorithm for parallelization. Column sampling is a simple but e ective technique borrowed from RandomForest [4]. While sparsity-aware learning is essential in other types of models such as linear models [9], few works on tree learning have considered this topic in a principled way. The algorithm proposed in this paper is the rstuni ed approach to handle all kinds of sparsity patterns. There are several existing works on parallelizing tree learn-ing [22, 19]. Most of these algorithms fall into the approximate framework described in this paper. Notably, it is also possible to partition data by columns [23] and apply the ex-act greedy algorithm. This is also supported in our frame-work, and the techniques such as cache-aware prefecthing can be used to bene t this type of algorithm. While most existing works focus on the algorithmic aspect of parallelization, our work improves in two unexplored system directions:out-of-core computation and cache-aware learning. This gives us insights on how the system and the algorithm can be jointly optimized and provides an end-to-end system that can handle large scale problems with very limited computing resources. We also summarize the comparison between our system and existing opensource implementations in Table 1.

Quantile summary (without weights) is a classical prob-lem in the database community [14, 24]. However, the ap-proximate tree boosting algorithm reveals a more general problem { nding quantiles on weighted data. To the best of our knowledge, the weighted quantile sketch proposed in this paper is the rst method to solve this problem. The weighted quantile summary is also not speci c to the tree learning and can bene t other applications in data science and machine learning in the future.

我们的系统实现了梯度增强[10]，它在功能空间中进行了添加优化。梯度树增强已成功用于分类[12]，学习排名[5]，结构化预测[8]以及其他领域。 XGBoost采用正则化模型来防止过度拟合。这类似于以前关于正则化贪婪森林的工作[25]，但简化了并行化的目标和算法。柱采样是一种从RandomForest [4]借来的简单但有效的技术。虽然稀疏感知学习在其他类型的模型（如线性模型[9]）中是必不可少的，但很少有关于树学习的工作以原则方式考虑该主题。本文提出的算法是处理各种稀疏模式的rstuni ed方法。有几个关于并行树学习的现有工作[22,19]。大多数这些算法都属于本文所述的近似框架。值得注意的是，也可以按列[23]对数据进行分区，并应用ex-act贪婪算法。我们的框架工作也支持这一点，并且可以使用诸如缓存感知预知之类的技术来获得这种类型的算法。虽然大多数现有的工作都集中在并行化的算法方面，但我们的工作在两个未开发的系统方向上进行了改进：核外计算和缓存感知学习。这为我们提供了有关如何联合优化系统和算法的见解，并提供了一个端到端系统，可以处理非常有限的计算资源的大规模问题。我们还总结了表1中我们的系统与现有开源实现之间的比较。

分位数摘要（无权重）是数据库社区中的经典问题[14,24]。然而，近似树提升算法揭示了一个更普遍的问题{加权数据上的分数。据我们所知，本文提出的加权分位数草图是解决该问题的第一种方法。加权分位数摘要也不是树学习的特定，并且可以在未来的数据科学和机器学习中获得其他应用。

6.END TO END EVALUATIONS

6.1 System Implementation

We implemented XGBoost as an open source package6. The package is portable and reusable. It supports various weighted classification and rank objective functions, as well as user de ned objective function. It is available in popular languages such as python, R, Julia and integrates naturally with language native data science pipelines such as scikit-learn. The distributed version is built on top of the rabit library7 for allreduce. The portability of XGBoost makes it available in many ecosystems, instead of only being tied to a specific platform. The distributed XGBoost runs natively on Hadoop, MPI Sun Grid engine. Recently, we also enable distributed XGBoost on jvm bigdata stacks such as Flink and Spark. The distributed version has also been integrated into cloud platform Tianchi8 of Alibaba. We believe that there will be more integrations in the future.

我们将XGBoost实现为开源包6。 该包装是便携式和可重复使用的。 它支持各种加权分类和秩目标函数，以及用户定义的目标函数。 它以流行的语言提供，例如python，R，Julia，并且自然地与语言本地数据科学管道集成，例如scikit-learn。 分布式版本建立在rabit库7之上，用于allreduce。 XGBoost的可移植性使其可用于许多生态系统，而不仅仅是绑定到特定平台。 分布式XGBoost在Hadoop，MPI Sun Grid引擎上本机运行。 最近，我们还在jvm bigdata堆栈（如Flink和Spark）上启用了分布式XGBoost。 分布式版本也已集成到阿里巴巴的云平台天池8中。 我们相信未来会有更多的整合。

6.2 Dataset and Setup

We used four datasets in our experiments. A summary of these datasets is given in Table 2. In some of the experiments, we use a randomly selected subset of the data either due to slow baselines or to demonstrate the performance of the algorithm with varying dataset size. We use a su x to denote the size in these cases. For example Allstate-10K means a subset of the Allstate dataset with 10K instances.

The rst dataset we use is the Allstate insurance claim dataset9. The task is to predict the likelihood and cost of an insurance claim given di erent risk factors. In the exper-iment, we simpli ed the task to only predict the likelihood of an insurance claim. This dataset is used to evaluate the impact of sparsity-aware algorithm in Sec. 3.4. Most of the sparse features in this data come from one-hot encoding. We randomly select 10M instances as training set and use the rest as evaluation set.

The second dataset is the Higgs boson dataset10 from high energy physics. The data was produced using Monte Carlo simulations of physics events. It contains 21 kinematic prop-erties measured by the particle detectors in the accelerator. It also contains seven additional derived physics quantities of the particles. The task is to classify whether an event corresponds to the Higgs boson. We randomly select 10M instances as training set and use the rest as evaluation set.

The third dataset is the Yahoo! learning to rank challenge dataset [6], which is one of the most commonly used bench-marks in learning to rank algorithms. The dataset contains 20K web search queries, with each query corresponding to a list of around 22 documents. The task is to rank the docu-ments according to relevance of the query. We use the o cial train test split in our experiment.

The last dataset is the criteo terabyte click log dataset11. We use this dataset to evaluate the scaling property of the system in the out-of-core and the distributed settings. The data contains 13 integer features and 26 ID features of user, item and advertiser information. Since a tree based model is better at handling continuous features, we preprocess the data by calculating the statistics of average CTR and count of ID features on the rst ten days, replacing the ID fea-tures by the corresponding count statistics during the next ten days for training. The training set after preprocessing contains 1.7 billion instances with 67 features (13 integer, 26 average CTR statistics and 26 counts). The entire dataset is more than one terabyte in LibSVM format.

我们在实验中使用了四个数据集。表2中给出了这些数据集的摘要。在一些实验中，由于基线较慢，我们使用随机选择的数据子集，或者演示具有不同数据集大小的算法的性能。在这些情况下，我们使用su x来表示大小。例如，Allstate-10K表示具有10K实例的Allstate数据集的子集。

我们使用的第一个数据集是Allstate保险索赔数据集9。任务是根据不同的风险因素预测保险索赔的可能性和成本。在实验中，我们简化了仅预测保险索赔可能性的任务。此数据集用于评估稀疏性感知算法在Sec中的影响。 3.4。此数据中的大多数稀疏功能都来自单热编码。我们随机选择10M实例作为训练集，并将其余部分用作评估集。

第二个数据集是来自高能物理学的希格斯玻色子数据集10。数据是使用物理事件的蒙特卡罗模拟生成的。它包含21个运动学特性，由加速器中的粒子探测器测量。它还包含七个额外的粒子派生物理量。任务是分类事件是否与希格斯玻色子相对应。我们随机选择10M实例作为训练集，并将其余部分用作评估集。

第三个数据集是Yahoo!学习排名挑战数据集[6]，这是学习排名算法最常用的基准标记之一。数据集包含20K Web搜索查询，每个查询对应于大约22个文档的列表。任务是根据查询的相关性对文档进行排名。我们在实验中使用了公式列车测试分组。

最后一个数据集是criteo terabyte click log dataset11。我们使用此数据集来评估系统在核外和分布式设置中的扩展属性。该数据包含13个整数功能和26个用户，项目和广告商信息的ID功能。由于基于树的模型更好地处理连续特征，我们通过计算前十天的平均CTR和ID特征的统计数据来预处理数据，在接下来的十天内用相应的计数统计数据替换ID特征。为了训练。预处理后的训练集包含17个具有67个特征的实例（13个整数，26个平均点击率统计和26个计数）。整个数据集的LibSVM格式超过1TB。

We use the rst three datasets for the single machine par-allel setting, and the last dataset for the distributed and out-of-core settings. All the single machine experiments are conducted on a Dell PowerEdge R420 with two eight-core Intel Xeon (E5-2470) (2.3GHz) and 64GB of memory. If not speci ed, all the experiments are run using all the available cores in the machine. The machine settings of the distribut-ed and the out-of-core experiments will be described in the corresponding section. In all the experiments, we boost trees with a common setting of maximum depth equals 8, shrink-age equals 0.1 and no column subsampling unless explicitly speci ed. We can nd similar results when we use other settings of maximum depth.

我们将前三个数据集用于单机par-allel设置，并将最后一个数据集用于分布式和核外设置。 所有单机实验均在戴尔PowerEdge R420上进行，配备两个八核Intel Xeon（E5-2470）（2.3GHz）和64GB内存。 如果未指定，则使用机器中的所有可用核心运行所有实验。 分布式和核外实验的机器设置将在相应的部分中描述。 在所有实验中，我们使用最大深度等于8的共同设置来提升树，收缩年龄等于0.1并且除非明确指定，否则不进行列子采样。 当我们使用其他最大深度设置时，我们可以得到类似的结果。

图10：Yahoo LTRC数据集上XGBoost和pG-BRT之间的比较。

表4：雅虎上500棵树的学习与排名比较 LTRC数据集

6.3 Classification

In this section, we evaluate the performance of XGBoost on a single machine using the exact greedy algorithm on Higgs-1M data, by comparing it against two other common-ly used exact greedy tree boosting implementations. Since scikit-learn only handles non-sparse input, we choose the dense Higgs dataset for a fair comparison. We use the 1M subset to make scikit-learn nish running in reasonable time. Among the methods in comparison, R’s GBM uses a greedy approach that only expands one branch of a tree, which makes it faster but can result in lower accuracy, while both scikit-learn and XGBoost learn a full tree. The results are shown in Table 3. Both XGBoost and scikit-learn give better performance than R’s GBM, while XGBoost runs more than 10x faster than scikit-learn. In this experiment, we also find column subsamples gives slightly worse performance than using all the features. This could due to the fact that there are few important features in this dataset and we can benefit from greedily select from all the features.

在本节中，我们使用Higgs-1M数据上的精确贪婪算法，通过将其与其他两种常用的精确贪婪树提升实现进行比较，评估XGBoost在单台机器上的性能。由于scikit-learn只处理非稀疏输入，我们选择密集的Higgs数据集进行公平比较。我们使用1M子集在合理的时间内运行scikit-learn nish。在比较的方法中，R的GBM使用贪婪的方法，只扩展树的一个分支，这使得它更快但可能导致更低的准确性，而scikit-learn和XGBoost都学习完整的树。结果显示在表3中.XGBoost和scikit-learn都比R的GBM提供更好的性能，而XGBoost的运行速度比scikit-learn快10倍。在此实验中，我们还发现列子样本的性能略差于使用所有功能。这可能是因为此数据集中的重要特征很少，我们可以从所有功能中贪婪地选择。

6.4 LearningtoRank

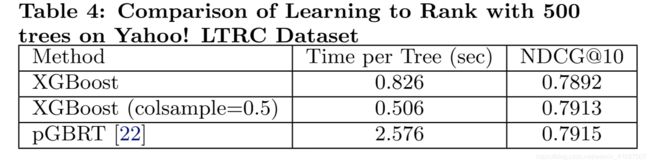
We next evaluate the performance of XGBoost on the learning to rank problem. We compare against pGBRT [22], the best previously pubished system on this task. XGBoost runs exact greedy algorithm, while pGBRT only support an approximate algorithm. The results are shown in Table 4 and Fig. 10. We nd that XGBoost runs faster. Interest-ingly, subsampling columns not only reduces running time, and but also gives a bit higher performance for this prob-lem. This could due to the fact that the subsampling helps prevent over tting, which is observed by many of the users.

我们接下来评估XGBoost在学习排名问题上的表现。 我们比较pGBRT [22]，这是此任务中最好的先前发布的系统。 XGBoost运行精确的贪心算法，而pGBRT仅支持近似算法。 结果显示在表4和图10中。我们发现XGBoost运行得更快。 有趣的是，二次采样列不仅减少了运行时间，而且还为这个问题提供了更高的性能。 这可能是由于子采样有助于防止过度使用，这是许多用户观察到的。

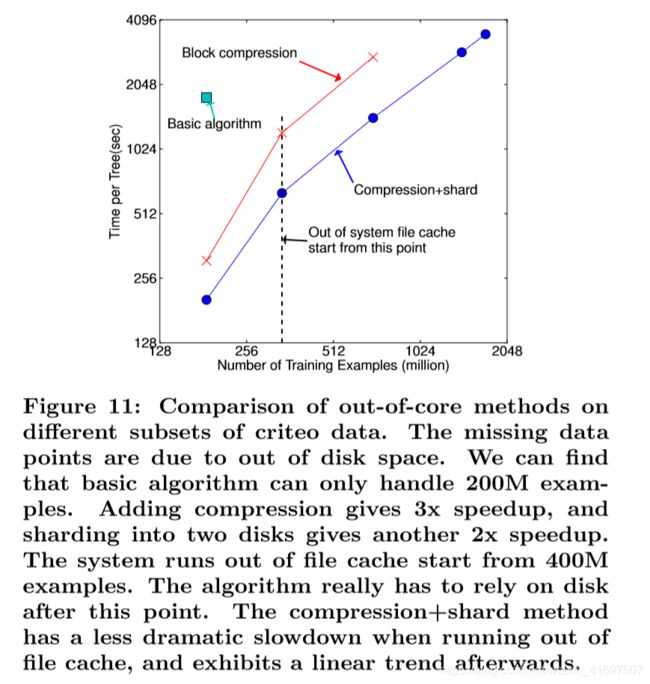
图11：对criteo数据的不同子集的核外方法的比较。 丢失的数据点是由于磁盘空间不足造成的。 我们可以发现基本算法只能处理200M的例子。 添加压缩可提供3倍的加速，并且分成两个磁盘可提供另外2倍的加速。 系统从400M示例开始耗尽文件缓存。 在此之后，算法确实必须依赖磁盘。 压缩+分片方法在用尽le缓存时具有不那么显着的减速，并且之后呈现线性趋势。

Figure 12: Comparison of different distributed systems on 32 EC2 nodes for 10 iterations on di erent subset of criteo data. XGBoost runs more 10x than spark per iteration and 2.2x as H2O’s optimized version (However, H2O is slow in loading the data, get-ting worse end-to-end time). Note that spark suffers from drastic slow down when running out of memory. XGBoost runs faster and scales smoothly to the full 1.7 billion examples with given resources by utilizing out-of-core computation.

图12：32个EC2节点上不同分布式系统的比较，在不同的criteo数据子集上进行10次迭代。 XGBoost每次迭代的运行次数比火花多10倍，H2O的优化版本运行2.2倍（但是，H2O在加载数据时速度慢，端到端时间更差）。 请注意，当内存不足时，火花会急剧减速。 通过利用核外计算，XGBoost运行速度更快，并且通过给定资源可以平滑地扩展到完整的17亿个示例。

6.5 Out-of-core Experiment

We also evaluate our system in the out-of-core setting on the criteo data. We conducted the experiment on one AWS c3.8xlarge machine (32 vcores, two 320 GB SSD, 60 GB RAM). The results are shown in Figure 11. We can nd that compression helps to speed up computation by factor of three, and sharding into two disks further gives 2x speedup. For this type of experiment, it is important to use a very large dataset to drain the system le cache for a real out-of-core setting. This is indeed our setup. We can observe a transition point when the system runs out of le cache. Note that the transition in the nal method is less dramatic. This is due to larger disk throughput and better utilization of computation resources. Our nal method is able to process 1.7 billion examples on a single machine.

我们还在criteo数据的out-of-core设置中评估我们的系统。 我们在一台AWS c3.8xlarge机器上进行了实验（32个vcores，两个320 GB SSD，60 GB RAM）。 结果显示在图11中。我们可以确定压缩有助于将计算速度提高三倍，并且分成两个磁盘进一步提供2倍的加速。 对于此类实验，使用非常大的数据集来排空系统文件缓存以实现真正的核外设置非常重要。 这确实是我们的设置。 当系统用完le缓存时，我们可以观察到一个转换点。 请注意，nal方法的转换不那么引人注目。 这是由于更大的磁盘吞吐量和更好的计算资源利用率。 我们的nal方法能够在一台机器上处理17亿个示例。

6.6 Distributed Experiment

Finally, we evaluate the system in the distributed setting. We set up a YARN cluster on EC2 with m3.2xlarge ma-chines, which is a very common choice for clusters. Each machine contains 8 virtual cores, 30GB of RAM and two 80GB SSD local disks. The dataset is stored on AWS S3 instead of HDFS to avoid purchasing persistent storage.

We rst compare our system against two production-level distributed systems: Spark MLLib [18] and H2O 12. We use 32 m3.2xlarge machines and test the performance of the systems with various input size. Both of the baseline systems are in-memory analytics frameworks that need to store the data in RAM, while XGBoost can switch to out-of-core set-ting when it runs out of memory. The results are shown in Fig. 12. We can nd that XGBoost runs faster than the baseline systems. More importantly, it is able to take advantage of out-of-core computing and smoothly scale to all 1.7 billion examples with the given limited computing re-sources. The baseline systems are only able to handle subset of the data with the given resources. This experiment shows the advantage to bring all the system improvement togeth-er and solve a real-world scale problem. We also evaluate the scaling property of XGBoost by varying the number of machines. The results are shown in Fig. 13. We can nd XGBoost’s performance scales linearly as we add more ma-chines. Importantly, XGBoost is able to handle the entire 1.7 billion data with only four machines. This shows the system’s potential to handle even larger data.

最后，我们在分布式设置中评估系统。我们在EC2上使用m3.2xlarge机器建立了一个YARN集群，这是集群的一个非常常见的选择。每台机器包含8个虚拟内核，30GB内存和两个80GB SSD本地磁盘。数据集存储在AWS S3而不是HDFS上，以避免购买持久存储。

我们首先将我们的系统与两个生产级分布式系统进行比较：Spark MLLib [18]和H2O 12.我们使用32 m3.2xlarge机器并测试具有不同输入尺寸的系统的性能。两个基线系统都是内存分析框架，需要将数据存储在RAM中，而XGBoost可以在内存不足时切换到核外设置。结果显示在图12中。我们可以发现XGBoost的运行速度比基线系统快。更重要的是，它能够利用核外计算，并在给定有限的计算资源的情况下平滑扩展到所有17亿个示例。基线系统只能处理具有给定资源的数据子集。该实验显示了将所有系统改进提供给解决方案并解决实际规模问题的优势。我们还通过改变机器的数量来评估XGBoost的缩放属性。结果显示在图13中。当我们添加更多的机器时，我们可以线性地找到XGBoost的性能标度。重要的是，XGBoost只需要四台机器即可处理整个17亿个数据。这表明系统有可能处理更大的数据。

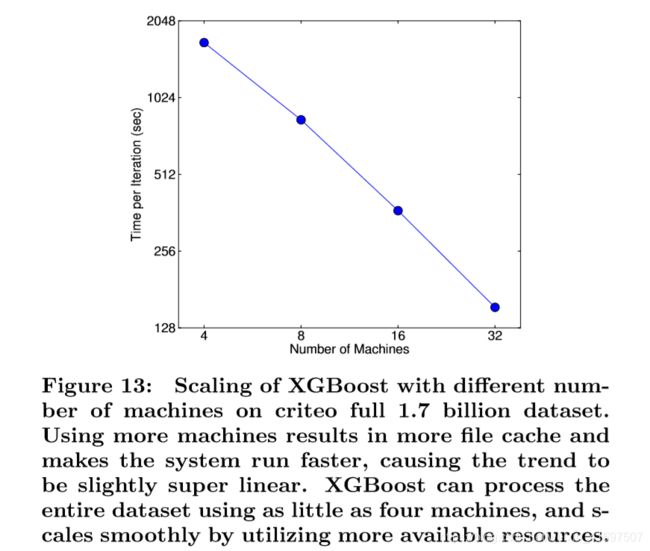
Figure 13: Scaling of XGBoost with different num-ber of machines on criteo full 1.7 billion dataset. Using more machines results in more le cache and makes the system run faster, causing the trend to be slightly super linear. XGBoost can process the entire dataset using as little as four machines, and scales smoothly by utilizing more available resources.

图13：在criteo完整的17亿数据集上使用不同数量的机器缩放XGBoost。 使用更多的机器会导致更多的缓存并使系统运行得更快，从而使趋势略微超线性。 XGBoost可以使用少至四台机器处理整个数据集，并通过利用更多可用资源顺利扩展。

7.CONCLUSION

In this paper, we described the lessons we learnt when building XGBoost, a scalable tree boosting system that is widely used by data scientists and provides state-of-the-art results on many problems. We proposed a novel sparsity aware algorithm for handling sparse data and a theoretically justi ed weighted quantile sketch for approximate learning. Our experience shows that cache access patterns, data com-pression and sharding are essential elements for building a scalable end-to-end system for tree boosting. These lessons can be applied to other machine learning systems as well. By combining these insights, XGBoost is able to solve real-world scale problems using a minimal amount of resources.

在本文中，我们描述了我们在构建XGBoost时学到的经验教训，XGBoost是一个可扩展的树推进系统，被数据科学家广泛使用，并提供了许多问题的最新结果。 我们提出了一种用于处理稀疏数据的新型稀疏感知算法和用于近似学习的理论上加权的加权分位数草图。 我们的经验表明，缓存访问模式，数据压缩和分片是构建可扩展的端到端系统以实现树提升的基本要素。 这些课程也可以应用于其他机器学习系统。 通过结合这些见解，XGBoost能够使用最少量的资源解决实际规模问题。

Acknowledgments

We would like to thank Tyler B. Johnson, Marco Tulio Ribeiro, Sameer Singh, Arvind Krishnamurthy for their valuable feedback. We also sincerely thank Tong He, Bing Xu, Michael Benesty, Yuan Tang, Hongliang Liu, Qiang Kou, Nan Zhu and all other con-tributors in the XGBoost community. This work was supported in part by ONR (PECASE) N000141010672, NSF IIS 1258741 and the TerraSwarm Research Center sponsored by MARCO and DARPA.

我们要感谢Tyler B. Johnson，Marco Tulio Ribeiro，Sameer Singh，Arvind Krishnamurthy提供的宝贵意见。 我们也衷心感谢Tong He，Bing Xu，Michael Benesty，Yuan Tang，刘洪亮，Qiang Kou，Nan Zhu以及XGBoost社区的所有其他贡献者。 这项工作部分由ONR（PECASE）N000141010672，NSF IIS 1258741和由MARCO和DARPA赞助的TerraSwarm研究中心提供支持。

8.REFERENCES

[1]R. Bekkerman. The present and the future of the kdd cup competition: an outsider’s perspective.

[2]R. Bekkerman, M. Bilenko, and J. Langford. Scaling Up Machine Learning: Parallel and Distributed Approaches. Cambridge University Press, New York, NY, USA, 2011.

[3]J. Bennett and S. Lanning. The netix prize. In

Proceedings of the KDD Cup Workshop 2007, pages 3{6, New York, Aug. 2007.

[4]L. Breiman. Random forests. Maching Learning, 45(1):5{32, Oct. 2001.

[5]C. Burges. From ranknet to lambdarank to lambdamart: An overview. Learning, 11:23{581, 2010.

[6]O. Chapelle and Y. Chang. Yahoo! Learning to Rank Challenge Overview. Journal of Machine Learning Research - W & CP, 14:1{24, 2011.

[7]T. Chen, H. Li, Q. Yang, and Y. Yu. General functional
matrix factorization using gradient boosting. In Proceeding of 30th International Conference on Machine Learning (ICML’13), volume 1, pages 436{444, 2013.

[8]T. Chen, S. Singh, B. Taskar, and C. Guestrin. E cient second-order gradient boosting for conditional random elds. In Proceeding of 18th Arti cial Intelligence and Statistics Conference (AISTATS’15), volume 1, 2015.

[9]R.-E. Fan, K.-W. Chang, C.-J. Hsieh, X.-R. Wang, and C.-J. Lin. LIBLINEAR: A library for large linear classi cation. Journal of Machine Learning Research, 9:1871{1874, 2008.

[10]J. Friedman. Greedy function approximation: a gradient boosting machine. Annals of Statistics, 29(5):1189{1232, 2001.

[11]J. Friedman. Stochastic gradient boosting. Computational Statistics & Data Analysis, 38(4):367{378, 2002.

[12]J. Friedman, T. Hastie, and R. Tibshirani. Additive logistic regression: a statistical view of boosting. Annals of Statistics, 28(2):337{407, 2000.

[13]J. H. Friedman and B. E. Popescu. Importance sampled learning ensembles, 2003.

[14]M. Greenwald and S. Khanna. Space-e cient online computation of quantile summaries. In Proceedings of the 2001 ACM SIGMOD International Conference on Management of Data, pages 58{66, 2001.

[15]X. He, J. Pan, O. Jin, T. Xu, B. Liu, T. Xu, Y. Shi,

A.Atallah, R. Herbrich, S. Bowers, and J. Q. n. Candela. Practical lessons from predicting clicks on ads at facebook. In Proceedings of the Eighth International Workshop on Data Mining for Online Advertising, ADKDD’14, 2014.

[16]P. Li. Robust Logitboost and adaptive base class (ABC) Logitboost. In Proceedings of the Twenty-Sixth Conference Annual Conference on Uncertainty in Arti cial Intelligence (UAI’10), pages 302{311, 2010.

[17]P. Li, Q. Wu, and C. J. Burges. Mcrank: Learning to rank using multiple classi cation and gradient boosting. In

Advances in Neural Information Processing Systems 20, pages 897{904. 2008.

[18]X. Meng, J. Bradley, B. Yavuz, E. Sparks,
S.Venkataraman, D. Liu, J. Freeman, D. Tsai, M. Amde,
S.Owen, D. Xin, R. Xin, M. J. Franklin, R. Zadeh,

M.Zaharia, and A. Talwalkar. MLlib: Machine learning in apache spark. Journal of Machine Learning Research, 17(34):1{7, 2016.

[19]B. Panda, J. S. Herbach, S. Basu, and R. J. Bayardo. Planet: Massively parallel learning of tree ensembles with mapreduce. Proceeding of VLDB Endowment, 2(2):1426{1437, Aug. 2009.

[20]F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel,
B.Thirion, O. Grisel, M. Blondel, P. Prettenhofer,
R. Weiss, V. Dubourg, J. Vanderplas, A. Passos,

D. Cournapeau, M. Brucher, M. Perrot, and E. Duchesnay. Scikit-learn: Machine learning in Python. Journal of Machine Learning Research, 12:2825{2830, 2011.

[21]G. Ridgeway. Generalized Boosted Models: A guide to the gbm package.

[22]S. Tyree, K. Weinberger, K. Agrawal, and J. Paykin. Parallel boosted regression trees for web search ranking. In

Proceedings of the 20th international conference on World wide web, pages 387{396. ACM, 2011.

[23]J. Ye, J.-H. Chow, J. Chen, and Z. Zheng. Stochastic gradient boosted distributed decision trees. In Proceedings of the 18th ACM Conference on Information and Knowledge Management, CIKM ’09.

[24]Q. Zhang and W. Wang. A fast algorithm for approximate quantiles in high speed data streams. In Proceedings of the 19th International Conference on Scienti c and Statistical Database Management, 2007.

[25]T. Zhang and R. Johnson. Learning nonlinear functions using regularized greedy forest. IEEE Transactions on Pattern Analysis and Machine Intelligence, 36(5), 2014.