深度学习---从入门到放弃（六）CNN入门

深度学习—从入门到放弃（六）CNN入门

1.CNN、RNN引入

• CNN
  1.主要应用于图像处理，CNN是一种通过卷积计算的前馈神经网络，其是受生物学上的感受野机制提出的，具有平移不变性，使用卷积核，最大的应用了局部信息，保留了平面结构信息。
  2.可以通过在空间上共享参数的形式减小计算资源
• RNN
  1.主要应用于时序相关的序列问题，比如自然语言处理（自然语言中语句长度通常不固定）。我们会在之后的教程中讲到RNN。
• DNN
  这里的DNN可以理解为我们之前所学到的简单的神经网络，由输入层，隐藏层和输出层组成，各个神经元分别属于不同的层，每个神经元和前一层的所有神经元相连接，信号从输入层向输出层单向传播。

2.CNN

卷积神经网络（convolutional neural network, CNN），是一种专门用来处理具有类似网格结构的数据的神经网络。卷积网络是指那些至少在网络的一层中使用卷积运算来替代一般的矩阵乘法运算的神经网络。

2.1卷积和边缘检测

2.1.1卷积

从本质上讲，卷积只是将一个矩阵（称为kernel或filter）与其他一些更大的矩阵（在我们的例子中是图像的像素）重复相乘。

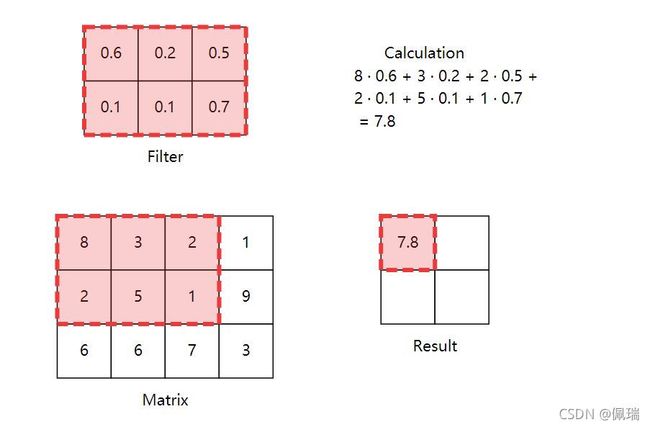
上图是一次卷积过程的例子，通过改变filter的大小和滑动的步长均可以得到不同的卷积结果。

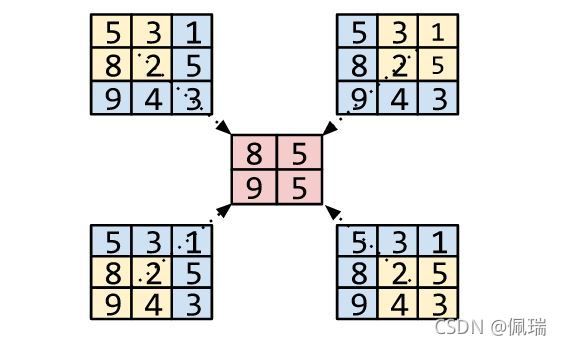
• 为了更好理解卷积的意义，在这里我们引入权值共享的概念，权值共享简单理解就是在现有filter的滑动过程中网络中的权值相同，即第一个隐藏层所有的神经元从输入层探测(detect)到的是同一种特征(feature)，只是从输入层的不同位置探测到(图片的中间，左上角，右下角等等)

不难看出，在CNN中一个filter只能提取一种空间特征，那么这么做的意义又在哪呢？

• 权值共享可以大大减少模型参数的个数，从而降低计算负担
  

2.1.2卷积输出大小

计算卷积之后输出的形状将如何改变？当你知道输入矩阵和卷积核的形状时，输出的形状是什么？

• $输出=输入-卷积核+1$

2.1.3 在 PyTorch 中演示卷积

看看下面的代码。在其中，我们定义了一个Net类，您可以使用内核实例化该类以创建神经网络对象。当您将网络对象应用于图像（或矩阵形式的任何东西）时，它会在该图像上对内核进行卷积。

class Net(nn.Module):
  """
 在这里我们定义了一个CNN的类
 如果我们选定了相应的卷积核，可以调用该类实现对于图像的卷积
  i.e. Net(kernel)(image)
  """
  def __init__(self, kernel=None, padding=0):
    super(Net, self).__init__()
    # Summary of the nn.conv2d parameters (you can also get this by hovering
    # over the method):
    # in_channels (int): Number of channels in the input image
    # out_channels (int): Number of channels produced by the convolution
    # kernel_size (int or tuple): Size of the convolving kernel
    # padding (int or tuple, optional): padding主要应用于边缘检测的场景中
    self.conv1 = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=2, \
                           padding=padding)

    # set up a default kernel if a default one isn't provided
    if kernel is not None:
      dim1, dim2 = kernel.shape[0], kernel.shape[1]
      kernel = kernel.reshape(1, 1, dim1, dim2)

      self.conv1.weight = torch.nn.Parameter(kernel)
      self.conv1.bias = torch.nn.Parameter(torch.zeros_like(self.conv1.bias))

  def forward(self, x):
    x = self.conv1(x)
    return x
    
# Format a default 2x2 kernel of numbers from 0 through 3
kernel = torch.Tensor(np.arange(4).reshape(2, 2))
# Prepare the network with that default kernel
net = Net(kernel=kernel, padding=0).to(DEVICE)

# set up a 3x3 image matrix of numbers from 0 through 8
image = torch.Tensor(np.arange(9).reshape(3, 3))
image = image.reshape(1, 1, 3, 3).to(DEVICE) # BatchSizeXChannelsXHeightXWidth

print("Image:\n" + str(image))
print("Kernel:\n" + str(kernel))
output = net(image) # Apply the convolution
print("Output:\n" + str(output))

Image:
tensor([[[[0., 1., 2.],
[3., 4., 5.],
[6., 7., 8.]]]])
Kernel:
tensor([[0., 1.],
[2., 3.]])
Output:
tensor([[[[19., 25.],
[37., 43.]]]], grad_fn=)

我们可以从结果中发现输入大小为 3×3，输出大小为 2×2。这是因为内核无法为图像的边缘生成值 - 当它滑动到图像的末端并以边界像素为中心时，它会重叠图像外未定义的空间。如果我们不想丢失这些信息，我们将不得不在边框上用一些默认值（例如 0）填充图像。可以预见，这个过程被称为padding。

上图中灰色部分即为用默认值填充的像素。基于padding的这种特性，它也被用于边缘检测。

• padding将默认值添加到图像的外边缘
• 步长调整过滤器在每次卷积后移动的距离。

2.2池化和下采样

在讲池化之前，我们先来回顾下之前讲的卷积中的过滤器，通过卷积之后的图像的信息不会发生变化，依旧保持全局不变性，那么想象一个场景：如果我们想要应用CNN去识别车辆，那么面对不同车辆轮胎大小不同的这种情况，我们当然不希望我们的网络仅仅因为轮胎大小这种局部微小差异进行分类。此时应用池化可以减小局部识别敏感度，即池化可以带来局部不变性。

2.2.1 案例引入

1.数据准备

为了可视化 CNN 的各个组件，我们将逐步构建一个简单的 CNN。我们将使用 EMNIST 字母数据集，它由手写字符的二值化图像组成(A,…,Z)。我们将训练一个 CNN 对图像进行分类X或 O。

2.同时应用多个卷积核进行卷积

class Net2(nn.Module):
  def __init__(self, padding=0):
    super(Net2, self).__init__()
    self.conv1 = nn.Conv2d(in_channels=1, out_channels=3, kernel_size=5,
                           padding=padding)

    # 第一个卷积核 - 主对角线
    kernel_1 = torch.Tensor([[[ 1.,  1., -1., -1., -1.],
                              [ 1.,  1.,  1., -1., -1.],
                              [-1.,  1.,  1.,  1., -1.],
                              [-1., -1.,  1.,  1.,  1.],
                              [-1., -1., -1.,  1.,  1.]]])

    # 第二个卷积核 - 其他对角线
    kernel_2 = torch.Tensor([[[-1., -1., -1.,  1.,  1.],
                              [-1., -1.,  1.,  1.,  1.],
                              [-1.,  1.,  1.,  1., -1.],
                              [ 1.,  1.,  1., -1., -1.],
                              [ 1.,  1., -1., -1., -1.]]])

    # 第三个卷积核 - 棋盘样方格图案
    kernel_3 = torch.Tensor([[[ 1.,  1., -1.,  1.,  1.],
                              [ 1.,  1.,  1.,  1.,  1.],
                              [-1.,  1.,  1.,  1., -1.],
                              [ 1.,  1.,  1.,  1.,  1.],
                              [ 1.,  1., -1.,  1.,  1.]]])


    # Stack all kernels in one tensor with (3, 1, 5, 5) dimensions
    multiple_kernels = torch.stack([kernel_1, kernel_2, kernel_3], dim=0)

    self.conv1.weight = torch.nn.Parameter(multiple_kernels)
    # Negative bias
    self.conv1.bias = torch.nn.Parameter(torch.Tensor([-4, -4, -12]))

  def forward(self, x):
    x = self.conv1(x)
    return x

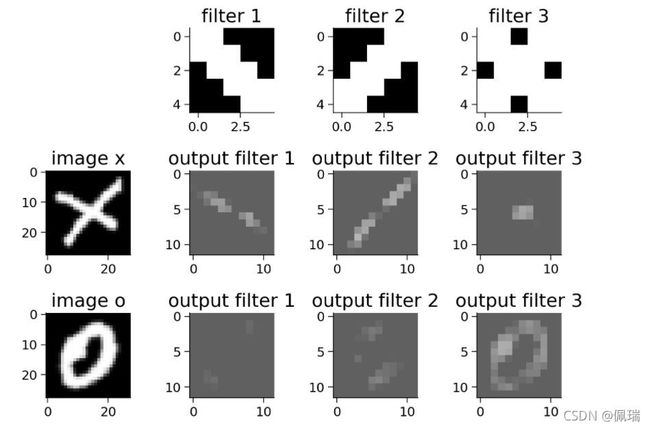
从上图中我们不难看出，这些过滤器被定制为对 X的响应较强；对角边缘滤波器强调
组成X的两条对角线，棋盘格图案对X的中心。

3.卷积后的 ReLU

到目前为止，我们已经讨论了卷积运算，它是线性的。但是神经网络的真正优势来自于非线性函数的结合。此外，在现实世界中，我们经常遇到输入和输出之间的关系是非线性和复杂的学习问题。

ReLU（修正线性单元）将非线性引入我们的模型，使我们能够学习更复杂的函数，可以更好地预测图像的类别。 有关ReLU在之前的教程中有所提及，这里不再赘述。

class Net3(nn.Module):
  def __init__(self, padding=0):
    super(Net3, self).__init__()
    self.conv1 = nn.Conv2d(in_channels=1, out_channels=3, kernel_size=5,
                           padding=padding)

    # 第一个卷积核 - 主对角线
    kernel_1 = torch.Tensor([[[ 1.,  1., -1., -1., -1.],
                              [ 1.,  1.,  1., -1., -1.],
                              [-1.,  1.,  1.,  1., -1.],
                              [-1., -1.,  1.,  1.,  1.],
                              [-1., -1., -1.,  1.,  1.]]])

    # 第二个卷积核 - 其他对角线
    kernel_2 = torch.Tensor([[[-1., -1., -1.,  1.,  1.],
                              [-1., -1.,  1.,  1.,  1.],
                              [-1.,  1.,  1.,  1., -1.],
                              [ 1.,  1.,  1., -1., -1.],
                              [ 1.,  1., -1., -1., -1.]]])

    # 第三个卷积核 - 棋盘样方格图案
    kernel_3 = torch.Tensor([[[ 1.,  1., -1.,  1.,  1.],
                              [ 1.,  1.,  1.,  1.,  1.],
                              [-1.,  1.,  1.,  1., -1.],
                              [ 1.,  1.,  1.,  1.,  1.],
                              [ 1.,  1., -1.,  1.,  1.]]])


    # Stack all kernels in one tensor with (3, 1, 5, 5) dimensions
    multiple_kernels = torch.stack([kernel_1, kernel_2, kernel_3], dim=0)

    self.conv1.weight = torch.nn.Parameter(multiple_kernels)
    # Negative bias
    self.conv1.bias = torch.nn.Parameter(torch.Tensor([-4, -4, -12]))

  def forward(self, x):
    x = self.conv1(x)
    x = F.relu(x)#引入ReLU
    return x

引入ReLU之后我们的过滤器对于X的响应变得更为明显，提取的三个空间特征也完美的展现出来了，因此利用ReLU可以更好的进行图像的识别。

2.2.2 池化

卷积层创建特征图，总结输入中特定特征（例如边缘）的存在。然而，这些特征图记录了特征在输入中的精确位置。这意味着图像中对象位置的微小变化可能会导致非常不同的特征图。 因此我们需要实现平移不变性。

解决此问题的常用方法称为下采样。下采样创建图像的较低分辨率版本，保留大型结构元素并删除一些可能与任务不太相关的精细细节。在 CNN 中，最大池化和平均池化用于下采样。这些操作缩小了隐藏层的大小，并产生了更具平移不变性的特征，后续层可以更好地利用这些特征。

与卷积层一样，池化层具有固定形状的窗口（池化窗口），它们系统地应用于输入。与过滤器一样，我们可以更改窗口的形状和步幅的大小。而且，就像过滤器一样，每次我们应用池化操作时，我们都会产生一个输出。

池化执行一种信息压缩，为输入的邻域提供汇总统计信息。经过池化后，大大减少了我们学到的特征值，也就大大减少了后面网络层的参数

• 在 Maxpooling 中，我们计算池化窗口中所有像素的最大值。
• 在 Avgpooling 中，我们计算池化窗口中所有像素的平均值。

上图为一个max-pooling的实例。

2.2.3 实现 MaxPooling

现在让我们在 PyTorch 中实现 MaxPooling，并观察 Pooling 对输入图像维度的影响。对 MaxPooling 层使用大小为 2 且步长为 2 的内核。

class Net4(nn.Module):
  def __init__(self, padding=0, stride=2):
    super(Net4, self).__init__()
    self.conv1 = nn.Conv2d(in_channels=1, out_channels=3, kernel_size=5,
                            padding=padding)

    # first kernel - leading diagonal
    kernel_1 = torch.Tensor([[[ 1.,  1., -1., -1., -1.],
                              [ 1.,  1.,  1., -1., -1.],
                              [-1.,  1.,  1.,  1., -1.],
                              [-1., -1.,  1.,  1.,  1.],
                              [-1., -1., -1.,  1.,  1.]]])

    # second kernel - other diagonal
    kernel_2 = torch.Tensor([[[-1., -1., -1.,  1.,  1.],
                              [-1., -1.,  1.,  1.,  1.],
                              [-1.,  1.,  1.,  1., -1.],
                              [ 1.,  1.,  1., -1., -1.],
                              [ 1.,  1., -1., -1., -1.]]])

    # third kernel -checkerboard pattern
    kernel_3 = torch.Tensor([[[ 1.,  1., -1.,  1.,  1.],
                              [ 1.,  1.,  1.,  1.,  1.],
                              [-1.,  1.,  1.,  1., -1.],
                              [ 1.,  1.,  1.,  1.,  1.],
                              [ 1.,  1., -1.,  1.,  1.]]])


    # Stack all kernels in one tensor with (3, 1, 5, 5) dimensions
    multiple_kernels = torch.stack([kernel_1, kernel_2, kernel_3], dim=0)

    self.conv1.weight = torch.nn.Parameter(multiple_kernels)
    # Negative bias
    self.conv1.bias = torch.nn.Parameter(torch.Tensor([-4, -4, -12]))
    self.pool = nn.MaxPool2d(kernel_size=2, stride=stride)#应用max-pooling

  def forward(self, x):
    x = self.conv1(x)
    x = F.relu(x)
    x = self.pool(x)  # pass through a max pool layer
    return x

我们可以观察到输出的大小是在 ReLU 部分之后看到的大小的一半，这是由于 Maxpool 层造成的。尽管输出的大小减少了，但输出中的重要或高级特征仍然保持不变。

3.构建一个CNN网络

3.1CNN五种结构组成

• 输入层：输入层一般代表了一张图片的像素矩阵。可以用三维矩阵代表一张图片。三维矩阵的长和宽代表了图像的大小，而三维矩阵的深度代表了图像的色彩通道。[Channels, Height, Width]
• 卷积层(Convolution Layer)
• 池化层(Pooling Layer)
• 全连接层:在经过多轮卷积层和池化层的处理之后，在CNN的最后一般会由1到2个全连接层来给出最后的分类结果。
  
  注：池化层到全连接层需要进行flatten的操作
• Softmax层:通过Softmax层，可以得到当前样例属于不同种类的概率分布。

3.2 网络架构

卷积 nn.Conv2d(in_channels=1, out_channels=32, kernel_size=3)
卷积 nn.Conv2d(in_channels=32, out_channels=64, kernel_size=3)
池化层 nn.MaxPool2d(kernel_size=2)
全连接层 nn.Linear(in_features=9216, out_features=128)
全连接层 nn.Linear(in_features=128, out_features=2)

class EMNIST_Net(nn.Module):
  def __init__(self):
    super(EMNIST_Net, self).__init__()
    #输入图像的大小为 [28, 28]
    #输入的图像Chanel=1，卷积之后产生的filter个数为32，卷积核为3*3
    self.conv1 = nn.Conv2d(1, 32, 3)
    #输入的图像Chanel=32，卷积之后产生的filter个数为64，卷积核为3*3
    self.conv2 = nn.Conv2d(32, 64, 3)
    #两次卷积后的图像大小变为28-3+1-3+1=24->[24,24]，max-pooling并引入ReLU之后输出大小变为原来的一半即[12,12]，此时图像大小为12*12=128
    #我们希望在传递线性层之前展平卷积层的输出，从而将形状 [BatchSize, Channels, Height, Width] 的输入转换为 [BatchSize, Channels\*Height\ *Width]，在这种情况下，从 [32, 64, 12, 12]（第二个卷积层的输出）到 [32, 64*12*12] = [32, 9216]。
    self.fc1 = nn.Linear(9216, 128)
    self.fc2 = nn.Linear(128, 2)#最终类别个数为2
    self.pool = nn.MaxPool2d(2)

  def forward(self, x):
    x = self.conv1(x)
    x = F.relu(x)
    x = self.conv2(x)
    x = F.relu(x)
    x = self.pool(x)
    x = torch.flatten(x, 1)
    x = self.fc1(x)
    x = F.relu(x)
    x = self.fc2(x)
    return x


# add event to airtable
atform.add_event('Coding Exercise 4: Implement your own CNN')

## Uncomment the lines below to train your network
emnist_net = EMNIST_Net().to(DEVICE)
print("Total Parameters in Network {:10d}".format(sum(p.numel() for p in emnist_net.parameters())))
train(emnist_net, DEVICE, train_loader, 1)

欢迎大家关注公众号奇趣多多一起交流！

深度学习—从入门到放弃(一)pytorch基础
深度学习—从入门到放弃（二）简单线性神经网络
深度学习—从入门到放弃（三)多层感知器MLP
深度学习—从入门到放弃（四）优化器
深度学习—从入门到放弃（五）正则化