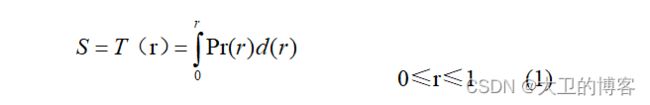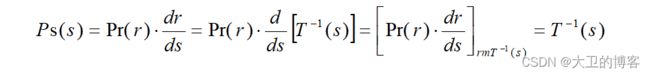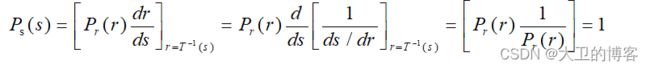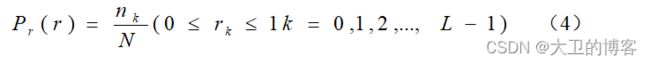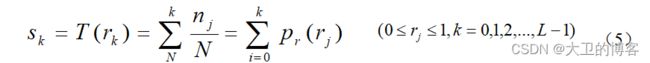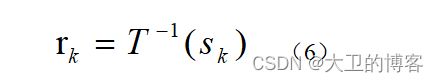数字图像处理——图像去雾技术的对比

前言

现代社会的发展总是伴随着环境的污染，雾霾现象发生越来越频繁，很大程度上影响我们的生活。雾霾是由空气中的灰尘和烟雾等小的漂浮颗粒产生的常见大气现象，这些漂浮的颗粒极大地吸收和散射光，导致拍摄图像质量下降。在雾霾影响下，视频监控，远程感应，自动驾驶等许多实际应用很容易受到威胁，检测和识别等高级计算机视觉任务很难完成。因此，图像去雾成为一种越来越重要的技术，有很重要的研究价值，同时也是一项充满挑战性的课题。为了解决这一问题，设计图像复原处理软件。

要求完成功能

1、 采用直方图均衡化方法增强雾天模糊图像，并比较增强前后的图像

和直方图:

2、查阅文献，分析雾天图像退化因素，设计一种图像复原方法，对比

该复原图像与原始图像以及直方图均衡化后的图像;

3、设计软件界面

---

一、 课程设计原理及设计方案

1.1 设计原理   

由于图像中存在噪声等干扰，使得图像模糊不清。可以采用图像增强的方

法对原图像处理，使图像变得清晰。而直方图均衡化是- -种常用的图像增强的

方法。图像模糊，其图像的像素分布不均匀，采用直方图均衡化的方法使其图

像像素分布均匀，从而达到均衡像素分布增强图像的目的。

1.1.1直方图均衡化

对于连续图像，设r和s分别表示被增强图像和变换后图像的灰度。为了简

单，在下面的讨论中，假定所有像素的灰度已被归- -化了，就是说，当时，

表示黑色;当时，表示白色;变换函数与原图像概率密度函数之间的关系

为:

    

 

式中: r为积分变量。式(1)的右边可以看作是r的累积分布函数(CDF)，因为CDF是r的函数，并单调地从0增加到1，所以这- -变换函数满足了前面所述的关于在内单值单调增加，对于，有的两个条件。由于累积分布函数是r的函数，并且单调的从0增加到1，所以这个变换函数满足对式(1) 中的r求导，则:

      

 

再把结果带入式 

 

正在上传…重新上传取消正在上传…重新上传取消    则得

 由以上推到可见，变换后的变量s的定义域内的概率密度是均匀分布的

由此可见，用r累积分布函数作为变换函数可产生一幅灰度级分布具有均匀概率密度的图像。其结果扩展了像素取值的动态范围。

上面的修正方法是以连续随机变量为基础进行讨论的。为了对图像进行数字处理，必须引入离散形式的公式。当灰度级是离散值的时候，可用频数近似代替概率值，即:

式中，L是灰度级数;是取第 k级灰度值的概率;是在图像中出现第 k级灰度的次数; N是图像中像素数。

通常把为得到均匀直方图的图像增强技术叫做直方图均衡化处理或直方图

线性化处理。式(1)的直方图均衡化累积分布函数的离散形式可由式(5) 表示:

 

其反变换为

 1.1.2雾天图像退化模型

在计算机视觉领域，通常使用雾天图像退化模型来描述雾霾等恶劣天气条件对图像造成的影响，该模型是McCartney首先提出。该模型包括衰减模型和环境光模型两部分。模型表达式为：

I(x)=J(x)e−rd(x)+A(1−e−rd(x))      (7)

其中，x是图像像素的空间坐标，H是观察到的有雾图像，F是待恢复的无雾图像，r表示大气散射系数，d代表景物深度，A是全局大气光，通常情况下假设为全局常量，与空间坐标x无关。

公式(7)中e−r(dx)e−r(dx)表示坐标空间x处的透射率，我们使用t(x)t(x)来表示透射率，于是得到下面的公式：

I(x)=J(x)t(x)+A(1−t(x))      （8）

由此可见，图像去雾过程就是根据I(x)求解J(x)的过程。要求解出J(x)，还需要根据I(x)求解出透射率t(x)和全局大气光A。

实际上，所有基于雾天退化模型的去雾算法就是是根据已知的有雾图像I(x)求解出透射率t(x)和全局大气光A。

估计全局大气光A:

1、暗通道去雾算法中的估计全局大气光A

先从暗原色通道中选取最亮的0.1%比例的像素电，然后选取原输入图像中这些像素具有的最大灰度值作为全局大气光A。RGB三通道中每一个通道都有一个大气光值。

2、分块递归思想估计全局大气光A

先将图像平均分为四个部分，然后分别求取四个部分中的平均亮度值，选取亮度值最大的块，将这个块平均分为四个块，选取最亮的块，当分解到块的大小达到一定阈值时，在这个块中选取亮度最大的点作为全局大气光A。

3、亮度最大值作为全局大气光A

选取输入图像中亮度最大的电的灰度值作为全局大气光A。

4、分段思量估计全局大气光A

观察一般的图像，天空部分一般分配在图像的上1/3部分，因此将图像水平分为3个部分，然后在最上的1/3部分使用暗通道估计算法估计全局大气光。

5、快速估计全局大气光A

首先求取输入图像RGB三通道中的最小值，即求取暗原色通道图像，然后对暗原色通道图像进行均值滤波，然后求取其中灰度值最大的点，接着求取输入图像RGB三通道中值最大的通道图像，然后求取出灰度值最大的点，然后将两个点的灰度值的平均值作为全局大气光A。

估计透射率t(x):

1、暗通道去雾算法

使用上面的方法先求取出全局大气光A，然后根据公式(8)可以得出：

t(x)=A−I(x)A−J(x)    (9)

首先可以确定的是t(x)的范围是[0, 1]，I(x)的范围是[0,255]，J(x)的范围是[0, 255]。A和I(x)是已知的，可以根据J(x)的范围从而确定t(x)的范围。已知的条件有：

0≤J(x)≤255,0≤I(x)≤A,0≤J(x)≤A,0≤t(x)≤1         (10)

t(x)≥A−I(x)A−0=A−I(x)A=1−I(x)A          (11）

结合式(10)和式(11)可得：

1−I(x)A≤t(x)≤1            (12)  

因此初略估计透射率的计算公式：

t(x)=1−I(x)A           (13)  

为了保证图片的自然性，增加一个参数w来调整透射率

t(x)=1−wI(x)A              (14)

2、精细化透射率

精细化透射率方法有：软抠图、双边滤波、导向滤波、恢复无雾图像。

估计出全局大气光A和透射率t(x)后，使用公式(14)可以计算得出去雾后的图像。实践表明这样去雾操作后，得到的无雾图像亮度会偏暗，可以使用自动对比度增强，亮度增强，伽马校正等图像处理方法进行处理，以便得效果更佳的无雾图像。

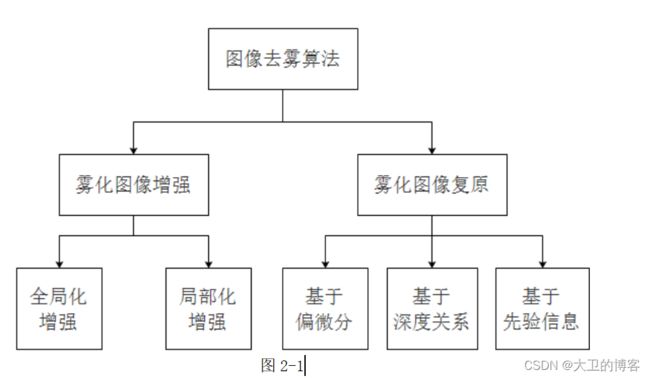
图像去雾算法可以分为两大类：一类是图像增强；另一类是图像复原。图1-1介绍了图像去雾算法的分类:

图2-1

二、课程设计的过程和结果

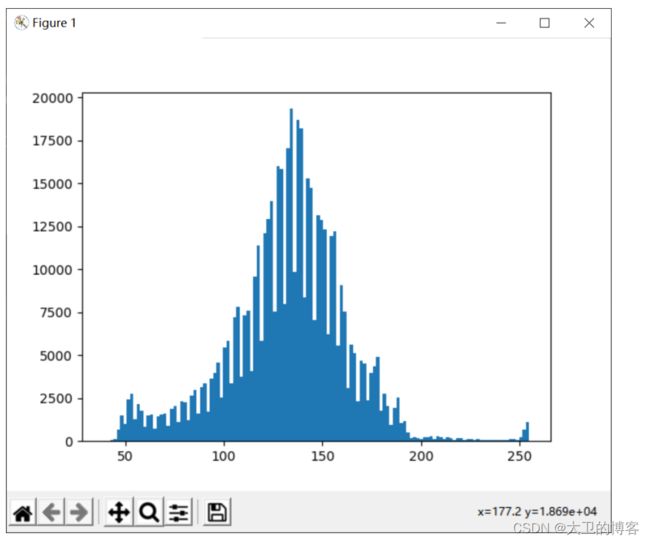
2.1原图像与直方图

# -*- coding: utf-8 -*-

from PIL import Image

from pylab import *

# 读取图像到数组中，并灰度化

im = array(Image.open('train.png').convert('L'))

# 直方图图像

hist(im.flatten(),128)

# 显示

show()

 原图像 3-1   

直方图3-2

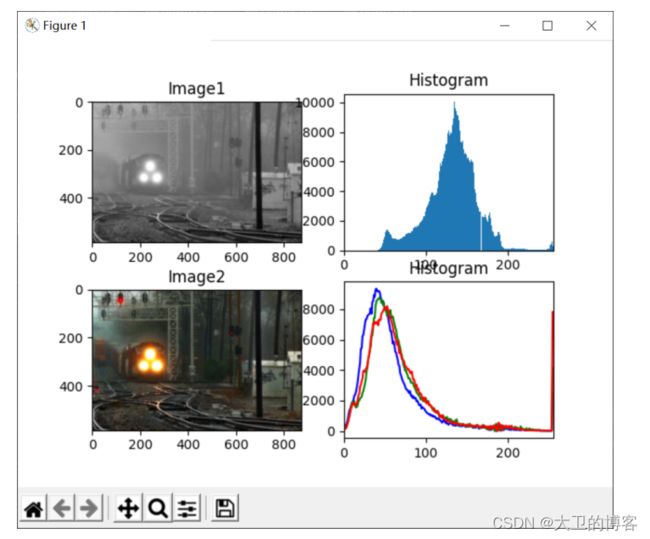
3.2原图像与均衡后图像

import cv2

import numpy as np

from matplotlib import pyplot as plt



img1 = cv2.imread('train.png', 0)

# 别忘了中括号 [img],[0],None,[256],[0,256]，只有 mask 没有中括号

hist1 = cv2.calcHist([img1], [0], None, [256], [0, 256])



img2 = cv2.imread('dehaze.png')

color = ('b', 'g', 'r')

for i, col in enumerate(color):

    histr = cv2.calcHist([img2], [i], None, [256], [0, 256])

    plt.subplot(224), plt.plot(histr, color=col),

    plt.xlim([0, 256]), plt.title('Histogram')



plt.subplot(221), plt.imshow(img1, 'gray'), plt.title('Image1')

plt.subplot(222), plt.hist(img1.ravel(), 256, [0, 256]),

plt.title('Histogram'), plt.xlim([0, 256])

plt.subplot(223), plt.imshow(cv2.cvtColor(img2, cv2.COLOR_BGR2RGB)), plt.title('Image2')

plt.show()

图3-3

# encoding:utf-8
import cv2
import numpy as np
import matplotlib.pyplot as plt

img_gray = cv2.imread('train.png', cv2.IMREAD_GRAYSCALE)
equ = cv2.equalizeHist(img_gray)
img2 = cv2.imread('dehaze.png')
color = ('b', 'g', 'r')
for i, col in enumerate(color):
    histr = cv2.calcHist([img2], [i], None, [256], [0, 256])
    plt.subplot(224), plt.plot(histr, color=col),
    plt.xlim([0, 256]), plt.title('Histogram')

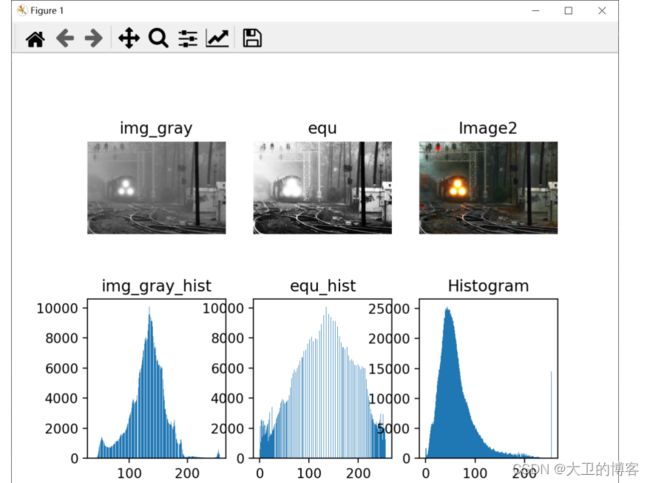
plt.subplot(231), plt.imshow(img_gray, cmap=plt.cm.gray), plt.title('img_gray'), plt.axis('off')  # 坐标轴关闭
plt.subplot(232), plt.imshow(equ, cmap=plt.cm.gray), plt.title('equ'), plt.axis('off')  # 坐标轴关闭
plt.subplot(233), plt.imshow(cv2.cvtColor(img2, cv2.COLOR_BGR2RGB)), plt.title('Image2'), plt.axis('off')
plt.subplot(234), plt.hist(img_gray.ravel(), 256), plt.title('img_gray_hist')
plt.subplot(235), plt.hist(equ.ravel(), 256), plt.title('equ_hist')
plt.subplot(236), plt.hist(img2.ravel(), 256),plt.title('Histogram')

plt.show()
cv2.waitKey(0)
cv2.destroyAllWindows()
print(img_gray.shape)

 图3-4

3.3原图与去雾图像对比

import cv2
import math
import numpy as np

def DarkChannel(im, sz):
    b, g, r = cv2.split(im)
    dc = cv2.min(cv2.min(r, g), b)
    kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (sz, sz))
    dark = cv2.erode(dc, kernel)
    return dark

def AtmLight(im, dark):
    [h, w] = im.shape[:2]
    imsz = h * w
    numpx = int(max(math.floor(imsz / 1000), 1))
    darkvec = dark.reshape(imsz, 1)
    imvec = im.reshape(imsz, 3)
    indices = darkvec.argsort()
    indices = indices[imsz - numpx::]
    atmsum = np.zeros([1, 3])
    for ind in range(1, numpx):
        atmsum = atmsum + imvec[indices[ind]]
    A = atmsum / numpx
    return A


def TransmissionEstimate(im, A, sz):
    omega = 0.95
    im3 = np.empty(im.shape, im.dtype)

    for ind in range(0, 3):
        im3[:, :, ind] = im[:, :, ind] / A[0, ind]

    transmission = 1 - omega * DarkChannel(im3, sz)
    return transmission

def Guidedfilter(im, p, r, eps):
    mean_I = cv2.boxFilter(im, cv2.CV_64F, (r, r))
    mean_p = cv2.boxFilter(p, cv2.CV_64F, (r, r))
    mean_Ip = cv2.boxFilter(im * p, cv2.CV_64F, (r, r))
    cov_Ip = mean_Ip - mean_I * mean_p
    mean_II = cv2.boxFilter(im * im, cv2.CV_64F, (r, r))
    var_I = mean_II - mean_I * mean_I
    a = cov_Ip / (var_I + eps)
    b = mean_p - a * mean_I

    mean_a = cv2.boxFilter(a, cv2.CV_64F, (r, r))
    mean_b = cv2.boxFilter(b, cv2.CV_64F, (r, r))
    q = mean_a * im + mean_b
    return q

def TransmissionRefine(im, et):
    gray = cv2.cvtColor(im, cv2.COLOR_BGR2GRAY)
    gray = np.float64(gray) / 255
    r = 60
    eps = 0.0001
    t = Guidedfilter(gray, et, r, eps)
    return t

def Recover(im, t, A, tx=0.1):
    res = np.empty(im.shape, im.dtype)
    t = cv2.max(t, tx)

    for ind in range(0, 3):
        res[:, :, ind] = (im[:, :, ind] - A[0, ind]) / t + A[0, ind]
    return res

if __name__ == '__main__':
    import sys

    try:
        fn = sys.argv[1]
    except:
        fn = 'train.png'

    def nothing(*argv):
        pass
    src = cv2.imread(fn)
    I = src.astype('float64') / 255
    dark = DarkChannel(I, 15)
    A = AtmLight(I, dark)
    te = TransmissionEstimate(I, A, 15)
    t = TransmissionRefine(src, te)
    J = Recover(I, t, A, 0.1)
    arr = np.hstack((I, J))
    cv2.imshow("contrast", arr)
    cv2.imwrite("dehaze.png", J * 255)
    cv2.imwrite("contrast.png", arr * 255)
    cv2.waitKey()

去雾后效果：

图3-5

去雾后图片直方图：

图3-6

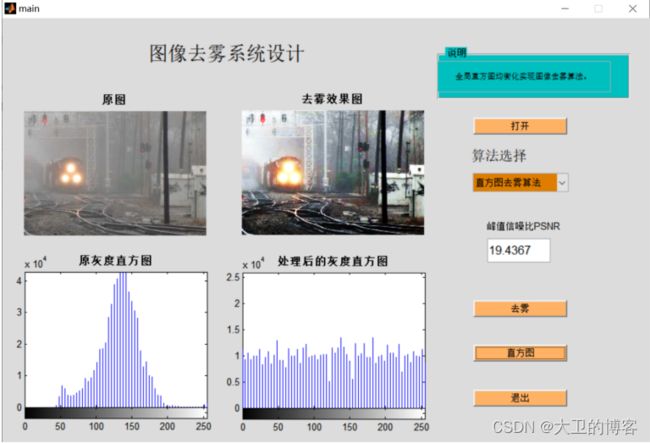
3.4设计 GUI 界面

界面设计如下：

---

总结

本文首先对图像去雾技术做了综述性的介绍。基于图像处理的图像增强方法具有对比度提高显著、图像细节突出、视觉效果明显的特点，该方法已经在实践中获得了广泛的应用。而基于物理模型的图像复原方法针对性强，得到的复原结果自然，且一般不会有信息损失，该技术必将获得更大的发展。

此次运用了一个对单图像去雾的简单有效的算法，叫暗通道先验算法。暗通道先验算法是基于室外图像统计规律的。应用这个先验算法模型使对单一图像进行去雾变得更加简单有效。由于暗通道检验算法是一种统计规律，因此对一些特殊的图像可能会不适用。对于景物颜色和大气光差别不大的图像，暗通道先验算法就不给力了，特别是对白雾传输的估计。