【数据分析报告】携程客户分析与流失预测

一、项目背景与目的

携程作为中国领先的综合性旅行服务公司，每天向超过2.5亿会员提供全方位的旅行服务，因此每天都会产生海量的用户行为数据，这些数据蕴含着丰富的信息资源。另外，客户是企业的重要资源，也是企业的无形资产，客户的流失，也就意味着资产的流失，因此客户流失率是考量业务成绩的一个非常关键的指标。

本项目致力于深入了解用户画像及行为偏好，找到最优算法，挖掘出影响用户流失的关键因素。从而能更好地完善产品设计、提升用户体验，针对不同类型的用户给出个性化运营策略。

本报告可以分为一下几个部分：

1. 探索性分析
2. 数据预处理与特征工程
3. 用户流失预测
4. RFM与用户画像分析

二、探索性分析

官方共提供2个数据集，分别为训练集userlostprob_train.txt和测试集userlostprob_test.txt。训练集为2016.05.15-2016.05.21期间一周的访问数据，测试集为2016.05.22-2016.05.28期间一周的访问数据。

本项目的评估标准官方用的是precision≥97%下，recall的最大值。我自己的话，选择准确度、AUC值。

精确度：（预测为流失且实际发生流失的样本数量）/（预测为流失的样本数量）
召回率：（预测为流失且实际发生流失的样本数量）/（实际流失的样本数量）

2.1 数据指标预览

查看数据集各特征字段，其中，label=1代表流失客户，label=0代表非流失客户。其他指标主要可以分为三种类型的数据指标：

• 用户相关特征：访问时长、访问次数、访问酒店数、使用时间、价格偏好、星级偏好、消费能力、价格敏感指数、用户价值
• 酒店相关特征：独立访问用户数、评论人数、评论数、历史取消率、酒店平均价格、最低价、商务属性指数等
• 订单相关特征：历史订单数、取消率、下单距离时长、访问日期、入住日期等

2.2 数据概况

#导入基础包
%matplotlib inline
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

import warnings
warnings.filterwarnings("ignore")


# 解决中文乱码问题
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

#显示全部特征
pd.set_option('display.max_columns', None)

#读取数据
df = pd.read_csv('./data/userlostprob_train.txt',sep='\t')
df.head()

查看数据情况，数据总体有一些特点：

• 除去标签id、label，一共有49个特征
• 数据形状(689945, 51)
• label流失用户有189357个，非流失用户有500588个。总体来看，流失用户占了27.4%

继续查看数据信息

# 查看每列数据
df.info()

# 查看数据形状
df.shape  # (689945, 51)

# label分布
df.label.value_counts()
# 0    500588
# 1    189357

可以看出：

• 除了d和arrival列特征为离散型特征（字符），其余均为连续性的数值型特征
• 时间格式：arrival和d的时间格式可以进行转换，并增加衍生字段来获取间隔天数
• 正负样本比例是：1: 2.7。有一点样本不平衡（因此评估指标加入AUC）

描述性统计

df.describe()

由描述性统计观察数据集的位置、集中趋势（平均值、中位数、众数），离散程度（方差、标准差、离散系数、四分位差），数据分布的统计图形（偏斜系数）。

由描述性统计可以看出，数据存在以下问题：

• 字段缺失，特征列存在不同程度的缺失情况，因此部分特征列的count数不全为689945，如historyvisit_7ordernum仅有82915条，存在数据缺失。后面进行缺失值填充的时候要注意分布的形态。
• 不应为负的数据特征列存在负值的情况，如：delta_price1（用户偏好价格-24小时浏览最多酒店价格）、lowestprice、delta_price2、customer_value_profit（客户近一年的价值），这些负值属于异常情况，后面需要对负值进行处理
• 数据特征列存在极值情况，方差很大，这样的数据需要对其极值进行处理。
• 数据分布形状呈现偏态，部分字段数据分布形态呈偏态状，如decisionhabit_user看出可能呈现右偏态的形式。后面对数据的缺失填充、异常值处理时，要结合偏态状况考虑。

查看缺失值比例

#查看缺失值比例
df.isnull().mean().sort_values(ascending=False)

看出字段缺失情况严重，其中historyvisit_7ordernum缺失值高达88%。除了arrival,d,h,sampleid,iforderpv_24h,sid,label外，其余44列字段各有不同程度缺失。因此后面要根据缺失情况，结合数据特征分布，选用合适的方法填充缺失值。

2.3 数据分布

查看数据分布情况，有助于特征工程根据数据分布选择合适的数据处理办法（包括缺失值、异常值处理，连续特征离散化），还有助于深入了解用户行为。

2.3.1 数据分布总览

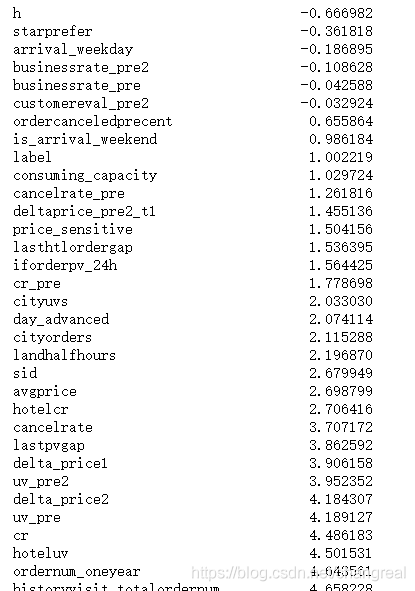
# 数据分布偏态情况
df.skew().sort_values()

当数据呈左右对称分布时，偏度系数等于0。偏度系数大于1或小于-1，视为严重偏斜分布；偏度系数为0.5～1或-1～-0.5，视为中等偏斜分布；偏度系数为**-0.5～0或0～0.5**，视为轻微偏斜分布。

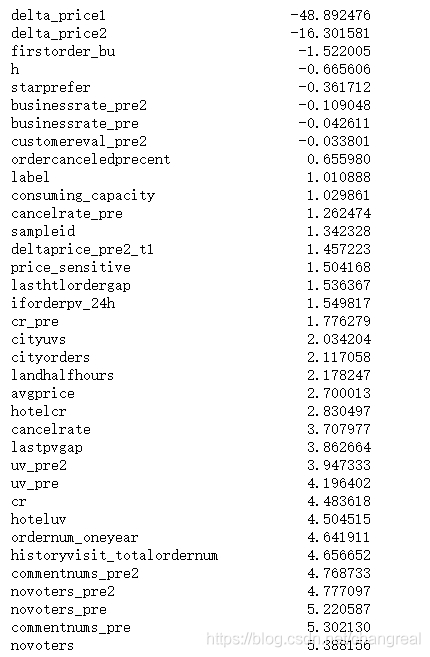
由上面可以看出，除了businessrate_pre2, businessrate_pre, customereval_pre2，其他数据基本都呈很大的偏态分布。

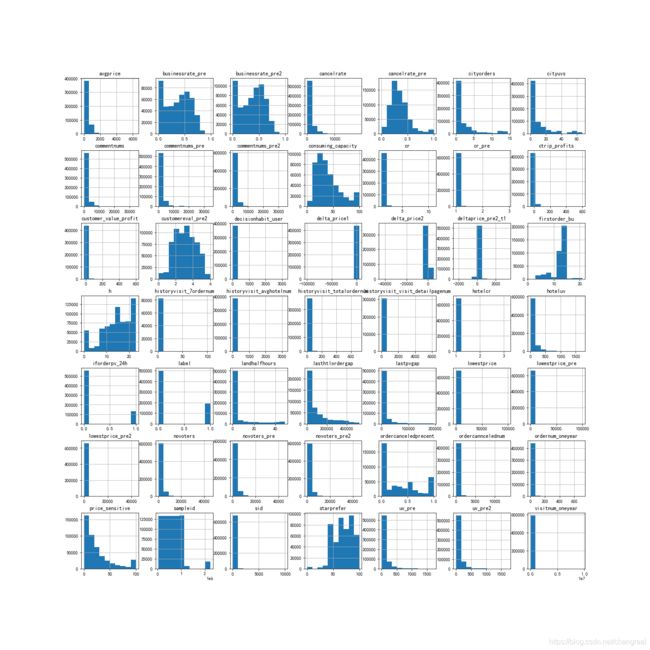
# 查看数据分布图
df.hist(figsize=(20,20))
plt.savefig('./images/data_distribution_raw.png')

2.3.2 预定日期和入住日期

# copy一份数据保存
cdf = df.copy()

# 构建访问时间和到达时间的表格
cdf_d = cdf.d.value_counts().to_frame().reset_index()
cdf_arrival = cdf.arrival.value_counts().to_frame().reset_index()
time_table = cdf_d.merge(cdf_arrival, how='outer', on='index')
time_table.fillna(0, inplace=True)
time_table.set_index('index',inplace=True)
time_table.sort_index(inplace=True)

# 获取字段
x = time_table.index
y1 = time_table.arrival
y2 = time_table.d

# 画图
plt.figure(figsize=(14,5))
plt.style.use('seaborn-colorblind')
plt.plot(x, y1, c='orange', label='入住人数')
plt.bar(x, y2, align='center', label='预定人数')
plt.title('访问和入住人数图',fontsize=20)
plt.xticks(rotation=45,fontsize=12)
plt.yticks(fontsize=14)
plt.xlabel('日期',fontsize=14)
plt.ylabel('人数', fontsize=14)
plt.legend(fontsize=14)

由图看出，520前预定人数和入住人数逐渐攀升，在520当天达到峰值，过了521，入住人数断崖式下降，随后酒店入住人数较为稳定，后面的两个下波峰是由于周末的原因。

2.3.3 访问时间段

plt.figure(figsize=(15,6))
plt.hist(cdf.h.dropna(), bins=48, align='mid')  # 由于是24h，所以分箱48，使得中间有间隔。
plt.title('访问时间段',fontsize=20);
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.xlabel('访问时间',fontsize=14); 
plt.ylabel('人数',fontsize=14);

由访问时间段可以看出，在 凌晨四五点的时候访问人数最少，此时大多数人在睡觉，因此这符合人的作息。随后访问人数在白天总体呈上升趋势，在17点-19点时稍微回落，因为此时是人的下班通勤时间或者晚饭时间，过了这段时间访问人数又开始逐渐上升，在22时达到峰值。

2.3.4 客户价值

plt.figure(figsize=(12, 4))
plt.style.use('bmh')

# 看看customer_value_profit 和 ctrip_profits 两者分布
plt.subplot(121)
plt.plot(cdf.index, cdf.customer_value_profit,linewidth=0.5)
plt.title('客户近1年价值')

plt.subplot(122)
plt.plot(df.index,df.ctrip_profits,linewidth=0.5)
plt.title('客户价值')

plt.savefig('./images/客户价值.png')

• 客户近一年的价值图和客户价值图大体上很相似，大多数人分布在0~100的范围内。另外，由于两个特征分布上非常接近，后面可以对customer_value_profit和ctrip_profits进行相关性分析验证，如果相关系数很大，可以考虑进行PCA降维。
• 不排除有些客户价值非常大，峰值达到了600，这些客户都可以在之后的分析中重点观察，因为他们是非常有“价值”的。但是这些峰值过大的客户，数据可能存在极值点过大的情况，因此需要对数据进一步处理。
• 另外，可以看出，两个字段都存在部分数据的客户价值为负，这些是异常值，需要处理。

2.3.5 消费能力指数

plt.figure(figsize=(12, 4))

plt.hist(df.consuming_capacity,bins=50,edgecolor='k')
plt.xlabel('消费能力指数')
plt.ylabel('人数')
plt.title('消费能力指数图')
plt.savefig('./images/消费能力指数图.png')

我们可以看到，消费能力指数的值范围是0-100。消费能力指数值基本呈现一个右偏的正态分布，平均消费能力在30附近，我们也能看到消费能力达到近100的人数也特别多，达到了21000多人，从这一点上，我们可以看到，酒店的入住客户中仍然存在较大群体的富裕人士。

2.3.6 价格敏感指数分布

plt.figure(figsize=(12, 6))
plt.hist(df['price_sensitive'].dropna(),bins = 50, edgecolor = 'k')
plt.xlabel('价格敏感指数') 
plt.ylabel('人数') 
plt.title('价格敏感指数分布')
plt.savefig('./images/价格敏感指数分布.png')
plt.show()

在价格敏感指数图中，出现两头存在极值现象，中间的分布也总体上呈现一个右偏正态分布，大部分人对价格并不敏感，对于这些用户来说，价格不是考虑的最重要因素。当然，我们也会发现，价格敏感指数为100时的人数也并不少，针对这一部分客户，我们可以考虑用一些打折优惠的方式吸引消费

2.3.6 入住酒店平均价格

plt.figure(figsize=(12, 4))
plt.subplot(121)
plt.hist(df.avgprice.dropna(),bins=50,edgecolor = 'k')
plt.xlabel('酒店价格')
plt.ylabel('偏好人数')
plt.title('酒店价格偏好')


# 由于酒店价格主要在2000以内，因此针对这个区间进行进一步可视化查看
plt.subplot(122)
plt.hist(df[df.avgprice<2000]['avgprice'].dropna(), bins = 50, edgecolor = 'k')
plt.xlabel('酒店价格')
plt.ylabel('偏好人数')
plt.title('2000元以内酒店偏好')

plt.savefig('./images/酒店偏好.png')

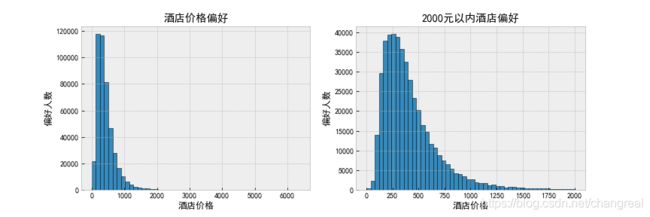
看出酒店价格偏好呈现一个正太分布微左偏态的分布，大多数人的价值偏好在150~600元之间，，在1500过后就没有什么人了。平均价格在250左右。

2.3.7 酒店星级偏好

plt.figure(figsize=(10, 4))
plt.hist(df.starprefer.dropna(), bins = 50, edgecolor = 'k')
plt.xlabel('星级偏好程度')
plt.ylabel('选择人数')
plt.title('酒店星级偏好')
plt.savefig('./images/酒店星级偏好.png')

分布规律性没有酒店价格偏好强，在40、60、80、100的分段存在极值情况，后面可以这些极值情况进行数据预处理。但总体来看，星级偏好主要集中在60~80之间。

2.3.8 订单取消率

plt.figure(figsize=(10, 4))
plt.hist(df.ordercanceledprecent.dropna(),bins=50,edgecolor = 'k')
plt.xlabel('订单取消率')
plt.ylabel('人数')
plt.title('订单取消率')

plt.savefig('./images/订单取消率.png')

存在大量的用户订单取消率为0的情况，说明大多数用户订了酒店后就会入住。而同时也存在部分极端用户，订单取消率为1的情况。订单取消率为0.5的用户第三多。

2.3.9 用户年订单数分布

plt.figure(figsize=(12, 6))
plt.hist(df[df["ordernum_oneyear"]<100]["ordernum_oneyear"].dropna(),bins = 50, edgecolor = 'k')
plt.xlabel('用户年订单数') 
plt.ylabel('数量') 
plt.title('用户年订单数100内的分布')
plt.savefig('./images/用户年订单数100内的分布.png')
plt.show()

绝大部分用户年订单数是小于50的，订单数在5次之内的人数占比比较大

2.3.10 新老客户流失率

# 新老客户，可以由sid来判断。流失与否，用label来判断
# 计算新老用户流失率
s_table = cdf[['label','sid']]
s_table['sid'] = np.where(s_table['sid']==1, 1, 0)  # 将sid处理为0和1两种情况，对应新客户和老客户
s_table['flag'] = 1  # 
s = s_table.groupby('sid').sum().reset_index()  # 按照新老用户区分，label是流失和没流失的人数，flag是新、老用户数
s['rate'] = s['label'] / s['flag']  # 新老用户流失率

# 画图
# 新老客户占比
plt.figure(figsize=(12, 5))
plt.subplot(121)
percent=[s['flag'][0]/s['flag'].sum(), s['flag'][1]/s['flag'].sum()]
# color=['steelblue','lightskyblue']
label=['老客','新客']
plt.pie(percent,autopct='%.2f%%',labels=label)
plt.title('新老客户占比')

# 流失率
plt.subplot(122)
plt.bar(s.sid, s.rate,align='center',tick_label=label,edgecolor = 'k')
plt.ylabel('流失率')
plt.title('新老客户中的客户流失率');

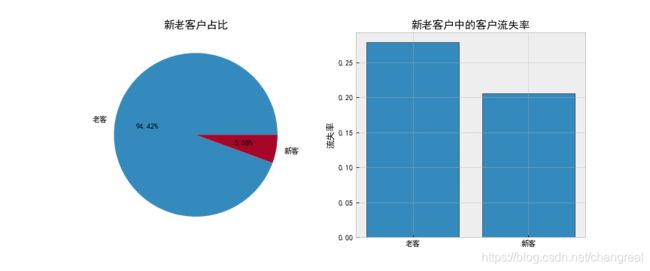
我们可以看到，众多客户中，94.42%的客户是老客户，新客只占5.58%，另外，老客的流失率达到28%，新客的流失率占20%，总体来说，我们应该采取措施，谨防用户流失，并且采取拉新手段获取更多新客户。

三、数据预处理

根据探索性分析中观察到的结果，我们需要对数据进行一系列预处理，包括数据格式转换、缺失值处理、异常值处理。

rawdf = df.copy()

3.1 去除不需要的字段与重复字段

sampleid列表示的是每一条的样本记录，firstorder_bu列表示首笔订单的bu，从实际意义来看，对用户是否流失影响不大。另外，label列也要去掉。

drop_columns = ['sampleid', 'firstorder_bu' ]
rawdf.drop(drop_columns, axis=1, inplace=True)

rawdf.drop_duplicates(inplace=True)

3.2 数据类型转换

时间特征处理
访问日期d和入住日期arrival字段为字符串类型，从实际意义来看，将其转换为星期几的int类型是种更好的方式。

另外是否为周末对实际的用户行为影响颇大，需新增判断是否为周末的特征列。

另外预定与入住间隔时间越久，用户的决策受影响的风先越大，所以也新构造关于间隔天数的特征列。

# 将两个日期变量由字符串转换为日期格式
rawdf['arrival'] = pd.to_datetime(rawdf['arrival'] )
rawdf['d'] = pd.to_datetime(rawdf['d'])

# 生成提前预定天数（衍生变量）（到达日期-访问日期间隔）（看提前多少天订）
rawdf['day_advanced'] = (rawdf['arrival']-rawdf['d']).dt.days

# 时间格式
rawdf['d'] = pd.to_datetime(df['d'], format = '%Y-%m-%d')
rawdf['arrival'] = pd.to_datetime(df['arrival'], format='%Y-%m-%d')

# 用户周几入住
rawdf['arrival_weekday'] = rawdf['arrival'].map(lambda x:x.weekday())

# 用户入住那天是否为休息日
def is_weekend(a):
    if int(a) in [0,1,2,3,4]:
        return 0 # 0代表是工作日
    else:
        return 1 # 1代表是周末

rawdf['is_arrival_weekend'] = rawdf['arrival_weekday'].map(lambda x: is_weekend(x))

rawdf.drop(labels=['d','arrival'], axis=1, inplace=True)

3.3 异常值处理

3.3.1负数处理

结合探索性分析中观察到的可视化图，

• delta_price1（用户偏好价格-24h浏览最多酒店价格）、delta_price2（用户偏好价格-24h浏览酒店平均价格）、lowestprice（当前酒店可定最低价格）三者理论上酒店价格不可能为负，并且由可视化图观察到数据分布比较集中，因此负值采取中位数处理。
• customer_value_profit（客户价值_近1年）、ctrip_profits(客户价值)也不应该为负值，结合可视化数据分布图看出它们的分布较为分散，因此将其填充为0

filter_one=['customer_value_profit','ctrip_profits']
filter_two=['delta_price1','delta_price2','lowestprice']

for f in filter_one:
    rawdf.loc[rawdf[f]<0, f] = 0

for f in filter_two:
    rawdf.loc[rawdf[f]<0, f] = rawdf[f].median()
    
rawdf[['customer_value_profit','ctrip_profits','delta_price1','delta_price2','lowestprice']].describe()

3.3.2 极值处理

由探索性分析中数据分布情况害能看出，较多特征有极大和极小的异常值，比如上文可视化的customer_value_profit，ctrip_profits，starprefer等。因此对所有字段使用1%和99%分位数替换超过上下线的值。

for i in rawdf.columns:
    value_1_percent =  np.percentile(rawdf[i], 1)  # # 1%的值
    value_99_percent = np.percentile(rawdf[i], 99) # 99%的值
    
    rawdf.loc[rawdf[i]<value_1_percent, i] = value_1_percent
    rawdf.loc[rawdf[i]>value_99_percent, i] = value_99_percent

# 查看表现
rawdf.skew().sort_values()

3.4 缺失值处理

常用缺失值处理方法

• 不处理（针对类似 XGBoost 等树模型）；
• 删除（缺失数据太多）；
• 插值补全，包括均值/中位数/众数/建模预测/多重插补/压缩感知补全/矩阵补全等；
• 分箱，缺失值一个箱；

3.4.1 删除

对于缺失率>80%的特征，删除对应的字段与特征

print('原来数据维度是:{}'.format(rawdf.shape))

# 定义删除空值行列的函数
def nan_drop(df,axi, rate=0.5):
    # rawdf.shape[1-0]是比如，如果要删除的是行，则看列的数量，然后*比率，即改行有多少列是缺失的
    # 反过来，如果要删除的是列，则看行的数量*比率，即该列有多少行缺失，从而删除
    # thresh是至少有多少存在则保留，否则删除
    df.dropna(axis=axi, how='any', thresh=df.shape[1-axi]*rate, inplace=True)

# 删除缺失值比例大于80%的行和列
nan_drop(rawdf, axi=0, rate=0.2)
nan_drop(rawdf, axi=1, rate=0.2)

print('删除缺失率较多的字段后的维度是:{}'.format(rawdf.shape))

原来数据维度是:(684406, 50)
删除缺失率较多的字段后的维度是:(684401, 49)

3.4.2 填充

对于缺失值小于80%的字段，结合数据分布形态填充。服从正态分布的使用均值填充，呈偏态分布的，使用中位数填充。

# 查看含有缺数的数据的偏态
rawdf.skew()[rawdf.isnull().mean(0)>0].sort_values()  # 查看含有缺数的数据的偏态

由数据偏态信息可知，对starprefer、businessrate_pre2、businessrate_pre、customereval_pre2、 ordercanceledprecent、consuming_capacity、cancelrate_pre进行均值填充。
对其他缺失的列进行中位数填充。

# 正态分布字段用均值填充
def nan_fill(df):
    filter_mean = ["businessrate_pre2","cancelrate_pre",
      "businessrate_pre",'starprefer','cancelrate_pre',
      'customereval_pre2','ordercanceledprecent',
      'consuming_capacity']
    for col in df.columns:
        if col in filter_mean:
            df[col] = df[col].fillna(df[col].mean())
        else:
            df[col] = df[col].fillna(df[col].median())
    return df

rawdf = nan_fill(rawdf)

四、特征工程

4.1 相关性分析

对用户特征相关分析

# 用户特征提取
user_features=['visitnum_oneyear','starprefer','sid','price_sensitive','ordernum_oneyear','ordercanncelednum','ordercanceledprecent','lastpvgap',
               'lasthtlordergap','landhalfhours','iforderpv_24h','historyvisit_totalordernum','historyvisit_avghotelnum','h',
               'delta_price2','delta_price1','decisionhabit_user','customer_value_profit','ctrip_profits','cr','consuming_capacity','avgprice']

# 生成用户特征的相关性矩阵
corr_mat = rawdf[user_features].corr()

# 绘制用户特征的相关性矩阵热度图
fig, ax = plt.subplots(figsize=(18,12))
sns.heatmap(corr_mat, xticklabels=True, yticklabels=True, square=False, linewidths=.5, annot=True, cmap="YlGnBu")
plt.savefig('./images/用户特征相关性分析热力图.jpg', dpi=400, bbox_inches='tight')
plt.show()

从热图中看出：

• delta_price1和delta_price2的相关性高达0.93，前者表示用户偏好价格-24小时浏览最多酒店价格，后者表示用户偏好价格-24小时浏览酒店平均价格，说明浏览24小时内浏览最多的酒店价格会影响到浏览酒店的平均价格，这可以理解为众数和平均数的关系。因此可以选择PCA提取一个主成分表示用户价格偏好。
• ordernum_oneyear和historyvisit_totalordernum的相关性高达0.93，两者都是表示用户1年内订单数，特征选取时可以只选择其一，这里选择ordernum_oneyear作为用户年订单数的特征，也可以用PCA降维；
• decisionhabit_user和historyvisit_avghotelnum的相关性达到了0.93，前者表示用户决策习惯，后者表示近三个月用户日均访问酒店数。说明决策时间久的用户近三个月访问酒店数的平均影响也越多，反过来也是，访问的酒店越多，该用户决策时间越久。
• customer_value_profit和ctrip_profits之间的相关性达到了0.86，前者表示用户近一年的价值，后者也表示用户价值，细分区别在于衡量的时间长度不同，这里也选择PCA提取一个主成分表示用户价值。
• consuming_capacity和avgprice之间的相关性达到了0.85，前者表示用户消费能力指数，后者表示酒店平均价格。很明显，消费能力越高，所选择的酒店平均价格大概率也越高。这里选择consuming_capacity来代表用户消费能力特征，也可以考虑用PCA降维综合这两个特征。

酒店信息特征的相关性分析

# 酒店信息特征相关性分析

# 酒店特征
hotel_features=['hotelcr','hoteluv','commentnums','novoters','cancelrate','lowestprice','cr_pre','uv_pre','uv_pre2','businessrate_pre',
                'businessrate_pre2','customereval_pre2','commentnums_pre','commentnums_pre2','cancelrate_pre','novoters_pre','novoters_pre2',
                'deltaprice_pre2_t1','lowestprice_pre','lowestprice_pre2','historyvisit_visit_detailpagenum']

# 生成酒店特征的相关性矩阵
corr_mat1 = rawdf[hotel_features].corr()

# 画图
fig, ax = plt.subplots(figsize=(18, 12))
sns.heatmap(corr_mat1, xticklabels=True, yticklabels=True, square=False, linewidths=.5, annot=True, cmap='Oranges')
plt.savefig('./images/酒店信息特征的相关性分析热力图.jpg',dpi=400, bbox_inches='tight')
plt.show()

• novoters和commentnums的相关性高达0.99，两个特征高度相关。因此取commentnums特征进入后续的预测与分析就好，或者选择PCA提取一个主成分表示酒店评论数
• cencelrate和commentnums三者的相关性也很高达到了0.86，可以看出酒店的评论数和取消率有很高的关系，可能是由于用户选择酒店后会查看酒店的相关评价，酒店的评论信息越多，用户对酒店也越了解，因此退订数量越少。因此要鼓励用户对酒店进行评价。
• uv_pre和uv_pre2的相关性达到了0.9，它们都表示24小时历史浏览次数最多的酒店的独立访客数信息，因此可以选择PCA提取一个主成分分析表示4小时历史浏览次数最多的酒店的独立访客数信息。
• commentnums_pre和novoters_pre的相关性高达0.99，两个特征高度相关。因此选择PCA提取一个主成分表示24小时历史浏览次数最多酒店点评数。
• commentnums_pre2和novoters_pre2的相关性高达0.99，两个特征高度相关。因此选择PCA提取一个主成分表示24小时历史浏览次数最多酒店点评数均值。

订单字段相关性分析

order_features = [ 'day_advanced', 'arrival_weekday', 'is_arrival_weekend' ,'ordercanceledprecent' ,'ordercanncelednum', 
         'lasthtlordergap', 'cityuvs', 'cityorders']

order_corr=rawdf[order_features].corr()   

# 画图
fig, ax = plt.subplots(figsize=(18, 12))
sns.heatmap(order_corr, xticklabels=True, yticklabels=True, square=False, linewidths=.5, annot=True, cmap='Blues')
plt.savefig('./images/订单信息特征的相关性分析热力图.jpg',dpi=400, bbox_inches='tight')
plt.show()

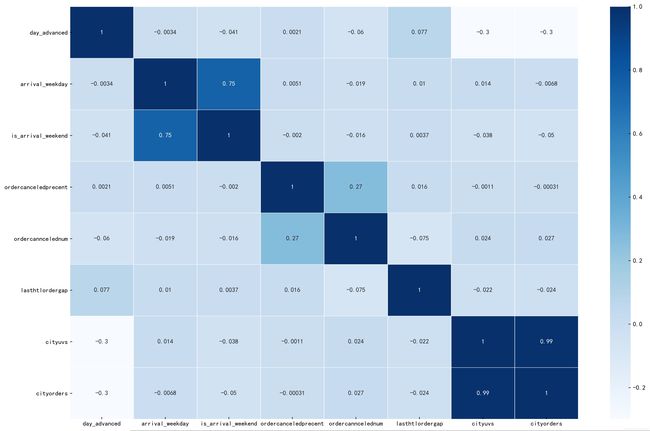
同理，看出cityorders和cityuvs存在0.99的相关性，需要PCA降维

4.2降维

降维是指在某些限定条件下，降低随机变量（特征）个数，得到一组“不相关”主变量的过程。这里使用主成分分析（PCA） 对相关度大于0.8的变量进行降维。

由上图的相关性分析矩阵，我们分别筛选用户和酒店很相关的维度进行降维度。

c_value=['customer_value_profit','ctrip_profits']                   # 用户价值维度
consume_level=['avgprice','consuming_capacity']                     # 用户消费水平
price_prefer=['delta_price1','delta_price2']                        # 用户偏好价格
ordernum_1_year = ['ordernum_oneyear', 'historyvisit_totalordernum']# 用户一年历史订单数

hotel_hot=['commentnums','novoters']                                # 酒店热度
hotel_hot_pre=['commentnums_pre','novoters_pre']                    # 24h内浏览次数最多的酒店热度
hotel_hot_pre2=['commentnums_pre2','novoters_pre2']                 # 24h内酒浏览酒店的平均热度
hotel_uv_pre = ['uv_pre', 'uv_pre2']                                # 24小时历史浏览次数最多的酒店的独立访客数

order_cityuvs_orders = ['cityorders','cityuvs']                     # 昨日访问当前城市同入住日期的app uv数和订单数

from sklearn.decomposition import PCA

pca=PCA(n_components=1)
rawdf['c_value']=pca.fit_transform(rawdf[c_value])
rawdf['consume_level']=pca.fit_transform(rawdf[consume_level])
rawdf['price_prefer']=pca.fit_transform(rawdf[price_prefer])
rawdf['ordernum_1_year'] = pca.fit_transform(rawdf[ordernum_1_year])
rawdf['hotel_hot']=pca.fit_transform(rawdf[hotel_hot])
rawdf['hotel_hot_pre']=pca.fit_transform(rawdf[hotel_hot_pre])
rawdf['hotel_hot_pre2']=pca.fit_transform(rawdf[hotel_hot_pre2])
rawdf['hotel_uv_pre']=pca.fit_transform(rawdf[hotel_uv_pre])
rawdf['order_cityuvs_orders']=pca.fit_transform(rawdf[order_cityuvs_orders])

rawdf.drop(c_value,axis=1,inplace=True)
rawdf.drop(consume_level,axis=1,inplace=True)
rawdf.drop(price_prefer,axis=1,inplace=True)
rawdf.drop(ordernum_1_year,axis=1,inplace=True)
rawdf.drop(hotel_hot,axis=1,inplace=True)
rawdf.drop(hotel_hot_pre,axis=1,inplace=True)
rawdf.drop(hotel_hot_pre2,axis=1,inplace=True)
rawdf.drop(hotel_uv_pre,axis=1,inplace=True)
rawdf.drop(order_cityuvs_orders,axis=1,inplace=True)

print('PCA降维后维度是:{}'.format(rawdf.shape))  # (684128, 40)

4.3 数据标准化与归一化

from sklearn.preprocessing import StandardScaler

y=rawdf['label']
x = rawdf.drop('label', axis=1)

scaler = StandardScaler()
scaler.fit(x)

X = scaler.transform(x)

五、建模预测

数据准备

from sklearn.model_selection import train_test_split, GridSearchCV
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size= 0.2,random_state=420)

5.1 逻辑回归

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report
from sklearn import metrics

lr = LogisticRegression()
lr.fit(X_train, y_train)
y_prob = lr.predict_proba(X_test)[:, 1]  # 预测1类的概率
y_pred = lr.predict(X_test)  # 模型对测试集的预测结果
print(y_prob)
print(y_pred)

fpr_lr, tpr_lr, threshold_lr = metrics.roc_curve(y_test, y_prob)  # # 获取真阳率、伪阳率、阈值
auc_lr = metrics.auc(fpr_lr, tpr_lr)
score_lr = metrics.accuracy_score(y_test, y_pred)

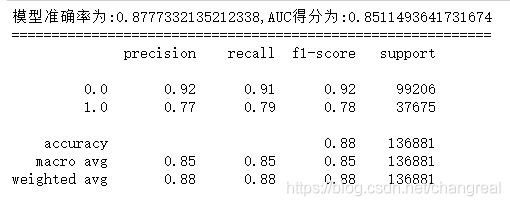
print('模型准确率为:{0}, AUC得分为:{1}'.format(score_lr, auc_lr)  )
print(classification_report(y_test, y_pred))

5.2 朴素贝叶斯

from sklearn.naive_bayes import GaussianNB

gnb = GaussianNB()                                                # 实例化一个LR模型
gnb.fit(X_train,y_train)                                          # 训练模型
y_prob = gnb.predict_proba(X_test)[:,1]                           # 预测1类的概率
y_pred = gnb.predict(X_test)                                      # 模型对测试集的预测结果
fpr_gnb,tpr_gnb,threshold_gnb = metrics.roc_curve(y_test,y_prob)  # 获取真阳率、伪阳率、阈值
auc_gnb = metrics.auc(fpr_gnb,tpr_gnb)                            # AUC得分
score_gnb = metrics.accuracy_score(y_test,y_pred)                 # 模型准确率


print('模型准确率为:{0},AUC得分为:{1}'.format(score_gnb,auc_gnb))
print('============================================================')
print(classification_report(y_test, y_pred, labels=None, target_names=None, sample_weight=None, digits=2))

5.3 支持向量机

from sklearn.svm import SVC


svc = SVC(kernel='rbf', C=1, max_iter=100 ).fit(X_train, y_train) # 径向基核函数，C是惩罚项，max_iter最大迭代次数，gamma, coef也常用
y_prob = svc.decision_function(X_test)
y_pred = svc.predict(X_test)
fpr_svc, tpr_svc, threshold_svc = metrics.roc_curve(y_test, y_prob)
auc_svc = metrics.auc(fpr_svc, tpr_svc)
score_svc = metrics.accuracy_score(y_test, y_pred)
print('模型准确率为:{0},AUC得分为:{1}'.format(score_svc,auc_svc))
print('============================================================')
print(classification_report(y_test, y_pred, labels=None, target_names=None, sample_weight=None, digits=2))

5.4 决策树

from sklearn import tree

dtc = tree.DecisionTreeClassifier()                              # 建立决策树模型
dtc.fit(X_train,y_train)                                         # 训练模型
y_prob = dtc.predict_proba(X_test)[:,1]                          # 预测1类的概率
y_pred = dtc.predict(X_test)                                     # 模型对测试集的预测结果 
fpr_dtc,tpr_dtc,threshod_dtc= metrics.roc_curve(y_test,y_prob)   # 获取真阳率、伪阳率、阈值
score_dtc = metrics.accuracy_score(y_test,y_pred)                
auc_dtc = metrics.auc(fpr_dtc,tpr_dtc) 
print('模型准确率为:{0},AUC得分为:{1}'.format(score_dtc,auc_dtc))
print('============================================================')
print(classification_report(y_test,y_pred,labels=None,target_names=None,sample_weight=None, digits=2))

5.5 随机森林

from sklearn.ensemble import RandomForestClassifier

rfc = RandomForestClassifier()                                     # 建立随机森林分类器
rfc.fit(X_train,y_train)                                           # 训练随机森林模型
y_prob = rfc.predict_proba(X_test)[:,1]                            # 预测1类的概率
y_pred=rfc.predict(X_test)                                         # 模型对测试集的预测结果
fpr_rfc,tpr_rfc,threshold_rfc = metrics.roc_curve(y_test,y_prob)   # 获取真阳率、伪阳率、阈值  
auc_rfc = metrics.auc(fpr_rfc,tpr_rfc)                             # AUC得分
score_rfc = metrics.accuracy_score(y_test,y_pred)                  # 模型准确率
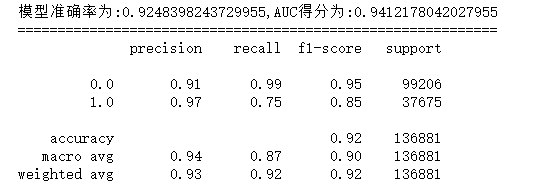
print('模型准确率为:{0},AUC得分为:{1}'.format(score_rfc,auc_rfc))
print('============================================================')
print(classification_report(y_test,y_pred,labels=None,target_names=None,sample_weight=None, digits=2))

5.6 XGBoost

import xgboost as xgb

# 读取训练集和测试集
dtrain = xgb.DMatrix(X_train, y_train)
dtest = xgb.DMatrix(X_test)

# 设置xgboost建模参数
params={'booster':'gbtree','objective': 'binary:logistic','eval_metric': 'auc',
    'max_depth':8,'gamma':0,'lambda':2,'subsample':0.7,'colsample_bytree':0.8,
    'min_child_weight':3,'eta': 0.2,'nthread':8,'silent':1}

# 训练模型
watchlist = [(dtrain,'train')]
bst=xgb.train(params,dtrain,num_boost_round=500,evals=watchlist)

#  输入预测为正确的概率
y_prob = bst.predict(dtest)
# 设置阈值为0.5，得到测试集的测试结果
y_pred = (y_pred >= 0.5)*1


# 获取真阳率、伪阳率、阈值
fpr_xgb,tpr_xgb,threshold_xgb = metrics.roc_curve(y_test,y_prob)   
auc_xgb = metrics.auc(fpr_xgb,tpr_xgb)    # AUC得分
score_xgb = metrics.accuracy_score(y_test,y_pred)    # 模型准确率
print('模型准确率为:{0},AUC得分为:{1}'.format(score_xgb,auc_xgb))
print('============================================================')
print(classification_report(y_test,y_pred,labels=None,target_names=None,sample_weight=None, digits=2))

5.7 模型比较

plt.style.use('bmh')
plt.figure(figsize=(16,16))

plt.plot(fpr_lr, tpr_lr, label='lr:%.3f' % score_lr )  # 逻辑回归
plt.plot(fpr_gnb,tpr_gnb,label='gnb:{0:.3f}'.format(score_gnb))         # 朴素贝叶斯
plt.plot(fpr_svc,tpr_svc,label='svc:{0:.3f}'.format(score_svc))         # 支持向量机
plt.plot(fpr_dtc,tpr_dtc,label='dtc:{0:.3f}'.format(score_dtc))         # 决策树
plt.plot(fpr_rfc,tpr_rfc,label='rfc:{0:.3f}'.format(score_rfc))         # 随机森林
plt.plot(fpr_rfc,tpr_rfc,label='xgb:{0:.3f}'.format(score_xgb))         # XGBoost

plt.legend(loc='lower right', prop={'size':25})
plt.xlabel('伪阳率')
plt.ylabel('真阳率')
plt.title('ROC曲线')
plt.savefig('./模型比较ROC曲线图.jpg',dpi=400, bbox_inches='tight')
plt.show()

六、RFM与用户画像分析

6.1 RFM分析

RFM模型，即为：

• R(Rencency):最近一次消费
• F(Frequency):消费频率
• M(Monetary):消费金额

由于本数据集并没有直接给出这三个指标，经过分析，选择选择lasthtlordergap(距离上次下单时长）、和经过PCA降维处理的ordernum_1_year（用户年订单数）、consume_level（消费能力水平）分别作为R、F、M值，从而对我们的用户群体进行分群

rfm_features = ['lasthtlordergap','ordernum_1_year','consume_level']
rfm = rawdf[rfm_features]

# 归一化（用于给RFM值打分）
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(rfm)
rfm = pd.DataFrame(scaler.transform(rfm), columns=['recency', 'frequency','monetary'] )

# 分箱
rfm['R'] = pd.qcut(rfm['recency'], 2)
rfm['F'] = pd.qcut(rfm['frequency'], 2)
rfm['M'] = pd.qcut(rfm['monetary'], 2)

# 根据分箱情况进行编码，二分类可以直接用标签编码方式
from sklearn.preprocessing import LabelEncoder

rfm['R'] = LabelEncoder().fit(rfm['R']).transform(rfm['R'])
rfm['F'] = LabelEncoder().fit(rfm['F']).transform(rfm['F'])
rfm['M'] = LabelEncoder().fit(rfm['M']).transform(rfm['M'])


#定义RFM模型，需要特别注意的是，R值代表距离上次消费时间间隔，值越小客户价值越高，与F和M值正好相反。
def get_label(r,f,m):
    if (r==0)&(f==1)&(m==1):
        return '高价值客户'
    if (r==1)&(f==1)&(m==1):
        return '重点保持客户'
    if((r==0)&(f==0)&(m==1)):
        return '重点发展客户'
    if (r==1)&(f==0)&(m==1):
        return '重点挽留客户'
    if (r==0)&(f==1)&(m==0):
        return '一般价值客户'
    if (r==1)&(f==1)&(m==0):
        return '一般保持客户'
    if (r==0)&(f==0)&(m==0):
        return '一般发展客户'
    if (r==1)&(f==0)&(m==0):
        return '潜在客户'
    
def RFM_convert(df):
    df['Label'] = df.apply(lambda x:get_label(x['R'], x['F'], x['M']), axis=1)
    
    df['R'] = np.where(df['R']==0, '高', '低')
    df['F'] = np.where(df['F']==1, '高', '低')
    df['M'] = np.where(df['M']==1, '高', '低')
    
    return df[['R','F','M','Label']]
    

rfm0 = RFM_convert(rfm)
rfm0.head()

# 可视化
# label_cnt = rfm0.groupby('Label').size()
label_cnt = rfm0['Label'].value_counts().values
labels = rfm0['Label'].value_counts().index
explode=[0.1,0.1,0.1,0,0,0,0,0]

plt.figure(figsize=(14,18))
# colors=['orangered','lightsalmon','sienna','seashell','chocolate','peru','sandybrown','peachpuff']
plt.pie(label_cnt, labels=labels,radius=1, explode=explode, autopct='%.1f%%',pctdistance=0.75,
        wedgeprops={'linewidth':0.5,'edgecolor':'black'}, 
        textprops={'fontsize':14,'color':'black'})
# plt.pie([1],radius=0.6,colors='w')
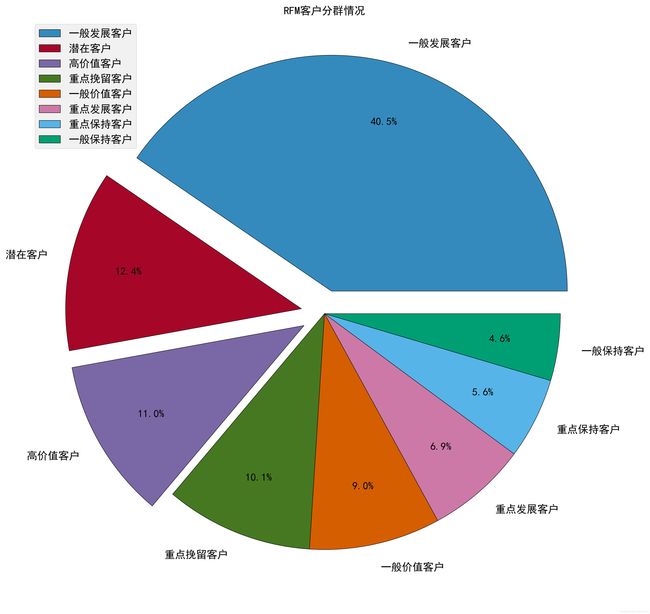
plt.title("RFM客户分群情况")
plt.legend(labels, fontsize=14, loc='best')
plt.savefig('./images/客户分群情况.jpg',dpi=400, bbox_inches='tight')
plt.show()

• 大部分客户是一般发展客户
• 潜在客户占比12.45%，这类客户有待开发；
• 高价值客户11%，重点保持客户5.6%，重点发展客户6.9%，这些都是要重点关注的客户群体

6.2 Kmeans构建用户画像

上面RFM模型只用到数据集中lasthtlordergap、ordernum_1_year、consuming_level三个直接相关变量，但这些变量并不能完全涵盖用户特征，所以，接下来用K-Means聚类的方法引入其他变量进一步探究分析，观察不同类别客户的特征。

6.2.1 查看重要特征

from xgboost import plot_importance

# 解决f特征名字
def ceate_feature_map(features):
    outfile = open('xgb.fmap', 'w')
    i = 0
    for feat in features:
        outfile.write('{0}\t{1}\tq\n'.format(i, feat))
        i = i + 1
    outfile.close()
ceate_feature_map(rawdf.columns)

fig, ax = plt.subplots(figsize=(16,16))
plot_importance(bst, height=0.5, ax=ax, max_num_features=40, color='green',fmap='xgb.fmap' )
plt.savefig('./images/xgbdata:image/png;base64,iVBORw0KGgoAAAANSUhEUgAABEYAAAOeCAYAAAAOchXZAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nOzde3xV1Z3//9ciObmQG7mRVFTQL0OBgkoxTIuVWyxQKAyFarE3RKetw7fwtWK1Vm1xflCnl7FF25naji2tbUVxpNNUR1QKUkGKGGQAByu0RAUScj25kJCTw/r9cU7SEAIC+8DOWef9fDx4JNlrn7U/K+f9UM6HfTHWWkREREREREREElE/vwsQEREREREREfGLGiMiIiIiIiIikrDUGBERERERERGRhKXGiIiIiIiIiIgkLDVGRERERERERCRhqTEiIiIiIiIiIglLjRERERFxjjHmJmOM7eXP1/yu7Xwwxhwwxkzyuw4REZF4lOx3ASIiIiLnyV+BD/bY1up1UmPMTcBN1tpJXueKoSuAo34XAWCMWQYMsdbe5HMpIiIiZ0SNEREREXHVcWttg99FXAjW2ka/axAREYlXupRGREREEo4x5lJjTJkxpsEY87oxZly3sWJjzO+NMc3GmHeNMbdGt083xljg58DEbpfnDIiOb4yeTdI5z03GmI3dfj5gjCk1xiyLzju129gEY8x2Y0yjMeZZY8zAs1zPCZfSRI+93RjzjDHmoDHmFmPMX40xO40xGdFaf2qMecMYU2uM+b4xJrnb6z9mjNkV/f081b2eaP2rjDFTjDGvGmN+Ed1+a/T3801gQfR309DtdRnGmF9H5zxijPnnbmMbjTGLouMtxpj/Mca8v9v4rcaYv0Rfu9oYk9ttbJ4xZk907NfGmIyz+d2JiIioMSIiIiKuuiz6Ybnzz1wAY0wSUAa0AKOBp4DfG2PSo6/7PtAfGA7MB1YaYy4CXgRygf8LbI5+nwsEz6Kmf47OuwDYHq1nMPAc8DjwASAE/OxcF93NlcC/AG8CdwMfAy6PbgeYA3wBmA5cDyyK1nMl8DTwbWBMdN+1xhjTbe4PAA8D34seg2jNudHXPR79fnC319wbnW8sUAp8uXtDikhDZTcwCmgAvh6tZx7wLeDW6OvfFz0Gxpi/B54AlhO5bGpo55iIiMiZ0qU0IiIi4qp3gEndfq6Ofv17Ig2RadbaSmPMA0QaBxOJNCi+TOReJBcR+aB9HPg/1tpDQIMx5ijQcY6X6RwFbrTW2m7bPgMcsNb+K0C0ns3GmP7WWi/3DSm31v7RGPM28Kq1dq8xphZIiY7/xFq7OXrMnwCfAB4i0oD4rbX2V9GxfwRqiDQeXou+9gpgpLV2f+fBrLXtQLsxpg1o7+X3821gBZGGyVigHXg/sC06vs1a+0D0mL8m0pQC+CLwb9ba56NjXwQujY7dAjxvrX08OvZ94AdE3kMREZEzosaIiIiIuKrDWnugl+0XR7/u7XYSRBp/O7thIpGzRtqJnBnSCiSdw/H797JtZY+mSGc9Q7tddmKInNV7CZGzPc5V6ym+7/R2t+8PAsXR7wcD5Z0D1toGY0wNkWZEZ2OkrHtT5AyNBh4BMoCtRJpE3X+vL3T7/hiR3wNEfg9PdqvnTf72e7kYmNLtd5cEZBpjUq21x86yPhERSVBqjIiIiEiieYfI5S9jum3LBKqMMWnAr4DPW2ufMsb0Aw71eP1x/vahvTvLiR/0S3rZp/kU9awH/qnbtgGc2Lg4Hy7v9v2l/G2dB4icKQNA9B4qhUBFt/17W0enU/1+fgn8yFr7vei823qMn+oGsm93r9UYMwH4lrX2I0R+d48RORMFIg2lbKDjNPWJiIicQPcYERERkUSzjciH7c8QuZ/HMCJnhowjcplJGpGzDi4HfgIUceIH/T8Do40xf2eMGRa9JwdEPqRfC2CMmQjMO8N6fgNcTeTeHx3AbOAVej/jJJZuMcZ8xBhTQuReI09Ftz8C/IMx5rPGmMuA/yByhseOM5z3z8CHjDGXGGNGGWOGRbdnAf2j25cTaRz11kDp6afAImPM1Gg99/K3Js2jwExgCJGGzBeA/z7DeUVERAA1RkRERCTBWGvDRJoPHwbeIPLB+xvW2meij729Hfgu8DJQSeSGoB/s9vqtRBom24hcWtJ5ZsgDwFhjzFvAHcD/d4b1VACfBO4jconIQmC2tbbW20rf02rgx0Tuq7KayO8Ba+1OYC5wF/A6kSbD3F4uATqVNUQaO/8L/BH4P9Ht/5fI/UJ2APlELp35YG8TdGet/U8iN2L9MZFLfI4QvYeItXYbsBj4UfR41wIzrbU6Y0RERM6YOfP/x4mIiIiIC6KPEV5lrV3lcykiIiK+0xkjIiIiIiIiIpKwdMaIiIiIiIiIiCQsnTEiIiIiIiIiIglLjRERERERERERSVhqjIiIiIiIiIhIwkr2uwCRC2Hjxo02NTXV7zJERERERETkPDh69GhNaWlp4bm8Vo0RSQjGGIYPH+53GSKevPvuu1x88cV+lyHiiXIsLlCOxRXKsrigM8fl5eUV5zqHLqUREYkTeoqYuEA5Fhcox+IKZVlcEIscqzEiCSE5WSdHSfwrLDynMwNF+hTlWFygHIsrlGVxQSxyrMaIJIRQKOR3CSKeVVVV+V2CiGfKsbhAORZXKMvigljkWI0RSQhJSUl+lyDiWWZmpt8liHimHIsLlGNxhbIsLohFjtUYEREREREREZGEpcaIJIRwOOx3CSKeNTc3+12CiGfKsbhAORZXKMvigljkWI0RSQiBQMDvEkQ8Kyoq8rsEEc+UY3GBciyuUJbFBbHIsRojkhA6Ojr8LkHEs+rqar9LEPFMORYXKMfiCmVZXBCLHKsxIiISJ4wxfpcg4plyLC5QjsUVyrK4IBY5VmNEEkJycrLfJYh4lpeX53cJIp4px+IC5VhcoSyLC2KRYzVGJCGEQiG/SxDxTKe7iguUY3GBciyuUJbFBbqURuQMJSUl+V2CiGfZ2dl+lyDimXIsLlCOxRXKsrggFjlWY0REJE7osdPiAuVYXKAciyuUZXFBLHKsxogkBP1HX1zQ0tLidwkininH4gLlWFyhLIsLYpFj3ZFSEsKfg39m8kOT/S5DxJO8QB51oTq/yxDxRDkWFyjH4gpluW+oW6L3wIvi4mLPc+iMEUkI2cm6flLi37SCaX6XIOKZciwuUI7FFcqyG+rr69mwYQO1tbV+l+KLyspKz3OoMSJOMMYsM8ZMOtX4cY5fwGpEzo/Gjka/SxDxTDkWFyjH4gplue85cuQIEydOpKOjg9GjRzNr1ixmzZrFG2+80eu2hoYG5s+fT3l5ObNnz6ampsbvJVxwgUDA8xy6lEYSQmu41e8SRDzb3bTb7xJEPFOOxQXKsbhCWe57vvGNb9DW1saePXuYN28ey5Yt6xrbuXPnSds2b97M8uXLKSkpoaGhgZ07d1JaWnrhC/dRTk6O5zl0xoi45KPGmE3GmNeNMSdcaJaRlOFXTSIxMz53vN8liHimHIsLlGNxhbLct2zatIn+/fszcOBAtm/fzrp167juuutYvHgxHR0dvW675pprKCkpYcuWLZSXl1NSUuL3Mi64WJwlk9S92yQSr+6///5JwPuttTPvv//+gUDOsmXLdnWOby/fvuyP3/0j4e1hMndmckXmFbQVtzGnaA5ZyVkUBgqZnD+Z+lA9pfmljM4cTU2ohtkDZ5OelM6gtEFMzJvIkfYjzCiYwbCMYTR1NPHxgR8nYAJc1v8yrs29lkPHDjGnaA6D0wfTfrydGYUzABieMZzxueO7xgelDQIL0wun02E7uCLrCj404ENd4wNTBpLaL5WPFnyU1nAr4waMY1zOuK7xvEAeWclZlOaX0tTRxEdyP8LVOVd3jWtNbq7p6pyrGZQ6yKk1ufg+aU2nX9OY7DEEO4JOrcnF90lrOv2aLkm7hLeOvuXUmlx8n7Sm915TXiCPK7KucGpN8fg+zbhkBocOHeK+++7jzjvv5JlnnuH6669n1qxZfOlLX6KsrIympiZGjhzJzJkz+fznP8+LL75IMBhkyJAhBINBVq5cCcDVV19NKBTCGMPhw4fp168fDQ0N1NbWkp6ezsGDBzl27BjHjx+nsrKS5ORkamtrqaur6xpvb28nFApRVVVFIBCgpqbmhPGOjg6OHTvGkSNHSElJoaqqimAwSGpqKgcPHiQcDtPa2kp1dTVpaWkcPnyYpqYmkpOTOXToENZaWlpaqK6u7prz6NGj9OvXj8OHDwPQ2NhITU1N13hra+sp11RTU0M4HKapqenw5Zdf/pNz+TxprLXn8jqRPsUYswx41Vr7jDHmJgBr7arO8cd+/5j9/Guf96c4kRiZkDuBTfWb/C5DxBPlWFygHIsrlOW+oW5JHd/5zncYNmwYc+bMYdasWTz11FOkpqYC8MgjjxAKhfjCF75w0rYvf/nLXfOsWLGCESNGMHfuXF/W4ZcjR44wcOBAysvLXystLb36XObQpTTiklM+wDpgvN+QR8Rvg9IG+V2CiGfKsbhAORZXKMt9x0svvcSjjz7KrFmz2LVrFzfccAO7d+8mHA7z7LPPMmrUKG699daTtq1cuZLVq1cDkbMsYnG/jXjT2ur9fpK6+aokBN1xW1ywrmad3yWIeKYciwuUY3GFstx3PPPMM13fz5o1iwceeIAvfvGLWGv52Mc+xqRJkxg4cOBJ26666ioWLlzIY489xogRI5gyZYqPq/BHcXHxe+/0HnQpjSSE1c+stjduv9HvMkQ8ufF9N/L44cf9LkPEE+VYXKAciyuU5b6hbkmd3yXEtYqKCgYPHqxLaUTeS9iG/S5BxLO6kP6nKfFPORYXKMfiCmVZXJCSkuJ5Dl1KIwlh8IDB6sRK3GtubiYzM9PvMkQ8UY7FBcqxuEJZFhdkZWV5nkNnjEhC6Ojo8LsEEc9qa2v9LkHEM+VYXKAciyuUZXFBLHKsxogkhORknRwl8S83N9fvEkQ8U47FBcqxuEJZFhfEIsdqjEhCOH78uN8liHgWi0eRifhNORYXKMfiCmVZXBCLHKsxIglBjRFxQVtbm98liHimHIsLlGNxhbIsLohFjtUYkYQQCAT8LkHEs1g8o13Eb8qxuEA5Flcoy+KCWORYjRFJCKFQyO8SRDyrrKz0uwQRz5RjcYFyLK5QlsUFscixGiOSEPr1U9Ql/qWlpfldgohnyrG4QDkWVyjL4oJY5FifFiUhqDEiLkhPT/e7BBHPlGNxgXIsrlCWxQWxyLE+LUpC6Ojo8LsEEc/q6+v9LkHEM+VYXKAciyuUZXFBLHKsxogkhOTkZL9LEPEsPz/f7xJEPFOOxQXKsbhCWRYXxCLH+rQoCaGioYJrH7rW7zJEPJlWMI11Nev8LkPEE+VYXKAciysSPct1S+r8LkFioKmpiczMTE9z6IwRSQhJJsnvEkQ8ywvk+V2CiGfKsbhAORZXKMu9q6+vZ8OGDdTW1sZkPzm/2tvbPc+hxogkhMaORr9LEPEskf9FR9yhHIsLlGNxhbL8N0eOHGHixIk0NDQwf/58ysvLmT17NjU1NV373HHHHTz33HMAp91PLqzi4mLPc6gxIgkhOznb7xJEPJtWMM3vEkQ8U47FBcqxuEJZ/ptvfOMbtLW1sWfPHpYvX87SpUuZMmUKO3fuBOCVV17hyJEjTJ8+HeCU+8mFV1lZ6XkONUYk7hhj0owxq40xLxtjfm+M6W+M2WiM+a4xpte2d8iGLnSZIjF3sO2g3yWIeKYciwuUY3GFshyxadMm+vfvz8CBA7nmmmsoKSlhy5YtlJeXU1JSQigU4rbbbuOSSy7h2WefBeh1P/FHLB7Xm7Rs2TLvlYhcQPfff/8ioM5ae/P999+fChjgPmCltfae3l6zo3zHsj9+94+Et4fJ3JnJFZlX0FbcxpyiOWQlZ1EYKGRy/mTqQ/WU5pcyOnM0NaEaZg+cTXpSOoPSBjExbyJH2o8wo2AGwzKG0dTRxMcHfpyACXBZ/8u4NvdaDh07xJyiOQxOH0z78XZmFM4AYHjGcMbnju8aH5Q2CCxML5xOh+3giqwr+NCAD3WND0wZSGq/VD5a8FFaw62MGzCOcTnjusbzAnlkJWdRml9KU0cTH8n9CFfnXN01rjW5uabJ+ZMZlDrIqTW5+D5pTadf08S8iQQ7gk6tycX3SWs6/Zo+kPkB3jr6llNrcvF90pree01D0odwRdYVTq3pbN6nfxj4DwSDQb7+9a9z5513sm7dOj760Y9SU1PDz3/+c5qampg0aRL/+Z//SXV1NXfddRdPP/0027dvp6SkhHfffZdHHnmEUChESUkJ6enp1NTUUFdXR3p6OgcPHqSjo4Njx45x5MgRUlJSqKqqIhgMkpqaysGDBwmHw7S2tlJdXU1aWhqHDx+mqamJ5ORkDh06hLWWlpYWqquru+Y8evQo/fr14/DhwwA0NjZSU1PTNd7a2ooxhsOHD9OvXz8aGhqora3tGj927BjHjx+nsrKS5ORkamtrT6i5vb2dUChEVVUVgUCgz6+psrKScDhMU1PT4csvv/wn5/IZ01hrz+V1Ir4xxvwb8J/W2vXGGBPd/Kq19upTvWb1M6vtjdtvvDAFipwnN77vRh4//LjfZYh4ohyLC5RjcUWiZ7luSR3f+c53GDZsGHPmzGHWrFmUlZV1ja9YsYIRI0awdetWpk6dynXXXcebb77JihUr+OUvf3nSfnPnzvVjGQmvoqKCwYMHU15e/lppaekpPxOeji6lkXi0F+g8V+3rwD8Czad7QUu45XzXJHLebanf4ncJIp4px+IC5VhcoSzDSy+9xKOPPsqsWbPYtWsXeXl5rF69GoictZCTk8Nll11GRUUFAK+//joXX3wxK1euPGk/8UdBQYHnOdQYkXj0U+CDxpiNwAeBx97rBelJ3q87E/HbqKxRfpcg4plyLC5QjsUVyjI888wzlJWVUVZWxujRo/nLX/7CE088wcyZMwmHw0yZMoXPfvaz/PGPf2TmzJk8+uijfPnLX2bBggUn7Sf+CAaDnudIjkEdIheUtbYVuKHH5kmne00/9QDFAXq6krhAORYXKMfiCmX5RJ2X0axdu/aE7VlZWaxateqk/XvuJ/4Ihbw/aEP3GJGEsHnzZjty5Ei/yxDx5NixY6SmpvpdhognyrG4QDkWVyjL4oLOHOseIyLvIRZdRBG/xeIZ7SJ+U47FBcqxuEJZFhfEIsdqjEhCSEpK8rsEEc8yMjL8LkHEM+VYXKAciyuUZXFBLHKsxoiISJxQg09coByLC5RjcYWyLC6IRY7VGJGEEA6H/S5BxLPGxka/SxDxTDkWFyjH4gplWVwQixyrMSIJIRAI+F2CiGeFhYV+lyDimXIsLlCOxRXKsrggFjlWY0QSQkdHh98liHhWV1fndwkininH4gLlWFyhLIsLYpFjNUZEROKEHq8uLlCOxQXKsbhCWRYXxCLHaoxIQkhOTva7BBHPdLqruEA5Fhcox+IKZVlcoEtpRM5QKBTyuwQRz6qqqvwuQcQz5VhcoByLK5RlcUEscqzGiCQEPYpMXJCZmel3CSKeKcfiAuVYXKEsiwtikWNdXyAJ4S8Nf2HCQxP8LkPEk5KcEl4Nvup3GSKeKMfiAuVY/FK3RDdLFTkfdMaIJITUfql+lyDi2dD+Q/0uQcQz5VhcoByLK5qbm/0uQcSzWORYjRFJCE3hJr9LEPFsfe16v0sQ8Uw5Fhcox+K3+vp6NmzYQG1trad5ioqKYlSRiH9ikWM1RiQhZCVl+V2CiGcTcyf6XYKIZ8qxuEA5Fj81NDQwf/58ysvLmT17NjU1Ndxwww1MmTKFr3zlKwBUVFTwqU99ihkzZnDvvfd2vXbx4sVMnTqV733vewBUV1f7sgaRWIpFjtUYEU+MMT84l/2MMVcZY646P1WdzKJntEv8C1k9XUnin3IsLlCOxU979uxh+fLlLF26lClTpvDUU09x/fXX84c//IHm5mZ27NjBsmXLuOOOO3j22Wc5dOgQL7/8MmVlZRw/fpznn3+eAwcOsH//fowxfi9HxLNY5FiNEfHEWnvbOe53VfTPBdESbrlQhxI5b3SjP3GBciwuUI7FT9dccw0lJSVs2bKF8vJycnJy+N///V+CwSAHDx5k0KBB7N+/nyuvvBKAwsJCGhsb2bx5M3PmzAFg8uTJbN26lby8PD+XIhITscixnkojZ8QYcw+wx1r7W2PM3cA+a+0aY8xGa+2k6D7pwBogG6gFrrfWdkTHuu/3APCJ6Pefs9aWnuKYy4AAcG10zunArcBGa+1GY8xN0V0XA0eAdqAY+Lm19sfd50prSyPvZ3k0h5tJT0pn2LXD2D9yP9MKpnGg9QBt4TaGZw5nU90mSnJKCJgAL9W/RGl+KfuO7gMiN1pbX7ueibkTCdkQrwZfZULeBPY27yUtKY0h6UNYV7OOaQXTaOxoZHfTbsbnjmdX0y7yAnkMShvUNV4XqmNfyz7GDRjHjsYdXJR6EUWpRV3jVceqOHTsEGOyx7CtYRtDM4aSF8jrGj/YdpC6UB2js0azpX4Lo7JGkZ2c3TWuNbm5plsvuZXXGl9zak0uvk9a0+nXdPPFN/PYocecWpOL75PWdPo1jR8wnn898K9OrcnF98nFNVVUVFBcXMzhw4f5zW9+Q0ZGBkOGDOH555/nu9/9LoMGDSI9PZ0JEyZw//33c+WVV/Lcc89x55138tRTT9GvXz+OHj1KKBTi7bffpqKigv79+1NcXExlZSWBQICcnBxqamrIycmhvb2d1tbWrvGUlBSysrKora0lNzeX1tZW2trausbT0tJIT0+nvr6e/Px8mpqaaG9v7xpPT08nJSWFYDBIQUEBwWCQUCjUNZ6RkUFSUhKNjY0UFhZSV1eHtZbCwkKqqqq6Hsva3NxMUVER1dXVGGPIy8ujurqa7OxswuEwLS0tWlMCrWnfvn2e7zNirNUlBvLejDHDgKXW2i8ZY/4b+KS1tqVHw2Ms8E1r7WxjzGxgk7W2ITrWtV/055sArLWrTnPMZcAIa+2njDHfAPYBwzi5MXIXUALsAq4D7rXWLuw+16qyVXZh+QmbROLOmKwx7Gja4XcZIp4ox+IC5Vj80vNxvStWrGDNmjVs2rSJ7OxsfvSjH5GRkcFNN93E1q1befjhhxkzZgx33HEHX/va15g3bx4lJSWUlZXx1ltvsXDhQnJzc31ajUhs1NfXk5ubS3l5+WulpaVXn8scupRGzoi19s/AxcaYbKDBWtvbtSnlwG5jzPPANOBoDA79y+jXt4GUHmPp0a9V1tpmoAIIAyddZNbPKOoS/9KS0vwuQcQz5VhcoByLn1auXMnq1asBaGxsJBgM8sYbbxAOh3nttde67rcwatQo3n33XRYtWgTAVVddxdatWwHYvXs3l156KeFw2J9FiMRQLHKsT4tyNrYBtwG/O8X4lcBma+1UIJfIJTCn0gr0BzCnv1tOzwZMO1AY/X76exXcKcX07KmIxJ8h6UP8LkHEM+VYXKAci58WLFjAE088wcyZMwmHw6xZs4avfOUrDBkyhPr6eubNmwfAww8/zKJFi+jfvz8AM2bM4Mknn+See+7ht7/9LVOnTqWlRffhk/gXixzrHiNyNtYALwODTzF+APh29H4kbcD208z1AvCkMeYzwN3ApjOs4XfAvxljSoncx+SMNHY0numuIn3Wupp1fpcg4plyLC5QjsVPAwYMYO3atSdse+WVV07a7+677z7h5+zsbMrKytiwYQNLliwhOzub1NTU81qryIVQXFzseQ7dY0QSwsaNG23nnblF4lVFRQWDB5+qLykSH5RjcYFyLK5QlsUFnTn2co8RnTEifYIxZmOPTUFr7T/EcP5YTSXim0Ag4HcJIp4px+IC5VhcoSyLC2KRYzVGpE/o/sSa8yEpKel8Ti9yQeTk5PhdgohnyrG4QDkWVyjL4oJY5Fg3X5WE0NHR4XcJIp7V1NT4XYKIZ8qxuEA5Flcoy+KCWORYjRFJCDpjRFygf9URFyjH4gLlWFyhLIsLdMaIyBnSTYbFBe3t7X6XIOKZciwuUI7FFcqyuCAWOVZjRBLC8ePH/S5BxLPW1la/SxDxTDkWFyjH4gplWVwQixyrMSIJQXfcFhfE4hntIn5TjsUFyrG4QlkWF8Qix2qMSEIIhUJ+lyDiWWVlpd8liHimHIsLlGNxhbIsLohFjtUYkYTQr5+iLvEvJSXF7xJEPFOOxQXKsbhCWRYXxCLH+rQoCUGNEXFBVlaW3yWIeKYciwuUY3GFsiwuiEWOk2NQh0if927wXa596Fq/yxDx5Mb33cjjhx/3uwwRT5RjcYFynJjqltT5XULM1dbWkpmZ6XcZIp7EIsf6Z3RJCK3HdcdtiX87Gnf4XYKIZ8qxuEA5Flfk5ub6XYKIZ7HIsRojkhACRk+lkfh3UepFfpcg4plyLC5QjhNXfX09GzZsoLa21u9SYkKP6xUXxCLHupRGEkKyUdQl/hWlFvldgohnyrG4QDlOTA0NDcyfP5+pU6dy7733MmfOHDZt2gRAMBhk7NixfP/732fx4sW8+eabTJ06lTvuuIPGxkZuueUWwuEwGRkZPProo33mpqdtbW1+lyDiWSxyrDNG4pAx5gfnsp8x5ipjzFXnp6q+rbGj0e8SRDxbV7PO7xJEPFOOxQXKcWLas2cPy5cvZ+nSpUyZMoUPfvCDlJWVUVZWxoc//GE+//nPU1ZWxvHjx3n++ec5cOAA+/fvZ82aNSxatIinn36agQMHsn79er+X0qW4uNjvEkQ8i0WO1RiJQ9ba285xv6uifxJOdnK23yWIeDatYJrfJYh4phyLC5TjxHTNNddQUlLCli1bKC8vp6SkBIBDhw5x5MgRxowZw+bNm5kzZw4AkydPZuvWrdxyyy1MnjwZgJqaGgoKCnxbQ0+VlZV+lyDiWSxyrOsL+jBjzD3AHmvtb40xdwP7rLVrjDEbrbWTovukA2uAbKAWuN5a2xEd677fA8Anot9/zlpbaoxZBgSAa6Ovnw7cCmy01m40xtwULWUxcARoB4qBn1trf9xLvXnAL4ABwGvW2tuMMauAvwAfBZKA0uixVgE5QJm19gFjzLa5jacAACAASURBVC+Af7fWbo2+5sfAX3vZ7yLgScACm6y19xhjhgArovVhrV3Ys7b25nbyfpZHc7iZ9KR0hl07jP0j9zOtYBoHWg/QFm5jeOZwNtVtoiSnhIAJ8FL9S5Tml7Lv6D4AhvYfyvra9UzMnUjIhng1+CoT8iawt3kvaUlpDEkfwrqadUwrmEZjRyO7m3YzPnc8u5p2kRfIY1DaoK7xulAd+1r2MW7AOHY07uCi1IsoSi3qGq86VsWhY4cYkz2GbQ3bGJoxlLxAXtf4wbaD1IXqGJ01mi31WxiVNYrs5Oyuca3JzTVdmnYpcwbOcWpNLr5PWtPp13RZ+mUMzxju1JpcfJ+0ptOv6bL0y8gL5Dm1Jhffp1ivqaamhubmZp566ilSUlKoqakhKSmJBx98kBtuuIEjR45QVVVFfn4+FRUVWGt59913qaioIDc3ly1btlBVVcUVV1xBRUUFaWlppKenU19fT35+Pk1NTbS3t1NcXExlZSXp6emkpKQQDAYpKCggGAwSCoW6xjMyMkhKSqKxsZHCwkLq6uqw1lJYWEhVVVXXUzqam5spKiqiuroaYwx5eXlUV1eTnZ1NKBSioqKia85AIEBOTg41NTXk5OTQ3t5Oa2tr13hKSgpZWVnU1taSm5tLa2srbW1tXeN9YU3hcJiWlhatKYHW1NLSQlVVVc+PgGfFWGs9TSDnjzFmGLDUWvslY8x/A5+01rb0aHiMBb5prZ1tjJlNpFnQEB3r2i/6800A1tpV0Z+XASOstZ8yxnwD2AcM4+TGyF1ACbALuA64t7fmgzHme8AOa+2vjTE/B54A5gNHrLV3GmN+BvwHcAPwurV2lTHmT8AMImeyzAGWAn+01v599FKgnvtdDqQCrwNbrLVXRBsj/wNMtdZu7e13+fOyn9uby28+w9+8SN80PGM4e1v2+l2GiCfKsbhAOU5M3R/Xu2LFCkaMGMGcOXOYPn0669atwxjD1772NebNm0dJSQllZWW89dZb3H777dTX1zNv3jx+8YtfcMkll/i4ihM1NjaSna0zqyW+dea4vLz8tdLS0qvPZQ5dStOHWWv/DFxsjMkGGqy1Lb3sVg7sNsY8D0wDjp7lYX4Z/fo20PMuUOnRr1XW2magAggD5hRzjQT+FP3+T8CI6Pe/6HGM9wP/ZIzZCGQAFwEbgA8DM4HfRffvbb8O4GtEGixZ3Y79/KmaIgDp/dJPNSQSN8Zkj/G7BBHPlGNxgXKcmFauXMnq1auByAexnJwcXnnlFcaOHYsxkb8eX3XVVWzdGvkr6e7du7n00ktpb29n4cKF3HfffX2qKQKRp+yIxLtY5FiNkb5vG3Abf2sW9HQlsNlaOxXIJXJZzKm0Av0BTOd/vaFns6UdKIx+P/0sa90DfCj6/YeiP/d2jDeBr0XPZvkXoM5aexx4Afge8KtT7QfcDjwA/CORy2k6NZ+usKPhs+0XifQ92xq2+V2CiGfKsbhAOU5MCxYs4IknnmDmzJmEw2GmTJnCH/7wB8aPH9+1z4wZM3jyySe55557+O1vf8vUqVP51a9+xc6dO3nwwQeZNWsWTz/9tI+rOFF+fr7fJYh4Fosc6x4jfd8a4GVg8CnGDwDfjt6PpA3Yfpq5XgCeNMZ8Brj7FPv8Dvg3Y0wpkXuWnI0HgF8aY24FtltrnzfGfLqX/f4FeNQYs5zIfURWR7evAT5kra04zX6/J3L/kWrgqDFm0JkUltov9SyXItL3DM0Yyv7W/X6XIeKJciwuUI4T04ABA1i7du0J2+67774Tfs7OzqasrIwNGzawZMkSsrOzufnmm7n55r55SXdTU1PX/SBE4lUscqx7jEifEG3EfAe4x1r7XKzn37hxo73yyitjPa3IBVVRUcHgwafqkYrEB+VYXKAciyuUZXFBZ4693GNEZ4zIWTPGFPO3szw6vWmt/dK5zmmtXQ+M9VTYaQQCgfM1tcgFE4tntIv4TTkWFyjH4gplWVwQixzrHiNy1qy1ldbaST3+nHNT5EIIhUJ+lyDiWSye0S7iN+VYXKAciyuUZXFBLHKsxogkhH79FHWJf+nperqSxD/lWFygHIsrlGVxQSxyrE+LkhD+9hAekfiVktLzidoi8Uc5Fhcox+IKZVlcEIscqzEiCSEcDvtdgohnwWDQ7xJEPFOOxQXKsbhCWRYXxCLHaoxIQkhO1n2GJf4VFBT4XYKIZ8qxuEA5Flcoy+KCWORYjRFJCDpjRFygf9URFyjH4gLlWFyhLIsLdMaIyBmy1vpdgohnerqSuEA5Fhcox+IKZVlcEIscqzEiCSEQCPhdgohnsXhGu4jflGNxgXIsrlCWxQWxyLEaI5IQ1A0XF8TiGe0iflOOxQXKsbhCWRYXxCLHuiOlJIS3m99m8kOT/S5DxJMPD/gwrzS84ncZIp4ox+IC5Tj+1C2p87uEPikjI8PvEkQ8i0WOdcaIJITj9rjfJYh41hZu87sEEc+UY3GBchy/6uvr2bBhA7W1tX6X0ickJSX5XYKIZ7HIsRojkhDS+qX5XYKIZ8Mzh/tdgohnyrG4QDmOTw0NDcyfP5/y8nJmz55NTU0NAHfccQfPPfdc136LFy9m6tSpfO973wOgoqKCT33qU8yYMYN7773Xl9rPl8bGRr9LEPEsFjlWY0R8Y4zZeKHmaw43x/JQIr7YVLfJ7xJEPFOOxQXKcXzas2cPy5cvZ+nSpUyZMoWdO3fyyiuvcOTIEaZPnw5AWVkZx48f5/nnn+fAgQPs37+fZcuWcccdd/Dss89y6NAhXn75ZZ9XEjuFhYV+lyDiWSxyrMaIJISMJF0/KfGvJKfE7xJEPFOOxQXKcXy65pprKCkpYcuWLZSXl1NSUsJtt93GJZdcwrPPPgvA5s2bmTNnDgCTJ09m69at7N+/nyuvvBKIfABz6SyLujrde0XiXyxyrJuvOsoYkwasAi4GGoDPAD8GLgLeBRYCXwcCwLVANjAdCAJroj/XAtcD9wIbrbUbjTE3RQ+xGDgCtAPFwM+BtdFj5gBl1toHzqLeop6vNcb8FPiRtfZ1Y8wjwH8Ab5/LMTqaO8j7WR7N4WbSk9IZdu0w9o/cz7SCaRxoPUBbuI3hmcPZVLeJkpwSAibAS/UvUZpfyr6j+wAY2n8o62vXMzF3IiEb4tXgq0zIm8De5r2kJaUxJH0I62rWMa1gGo0djexu2s343PHsatpFXiCPQWmDusbrQnXsa9nHuAHj2NG4g4tSL6IotahrvOpYFYeOHWJM9hi2NWxjaMZQ8gJ5XeMH2w5SF6pjdNZottRvYVTWKLKTs7vGtSY31zQmawyAU2ty8X3Smk6/prHZY9nbstepNbn4PmlNp1/T2OyxbKrf5NSaXHyfuq+ppqaGpKQkgsEga9asITU1lUceeYShQ4cyd+5cnn76ad58802qqqrIy8vjnXfeIRwOc/DgQSZMmMD999/PlVdeyXPPPcddd91FRUUFgUCAnJwcampqyMnJob29ndbWVoqLi6msrCQlJYWsrCxqa2vJzc2ltbWVtra2rvG0tDTS09Opr68nPz+fpqYm2tvbu8bT09NJSUkhGAxSUFBAMBgkFAp1jWdkZJCUlERjYyOFhYXU1dVhraWwsJCqqioyMzMBaG5upqioiOrqaowx5OXlUV1dTXZ2Ns3NzVRUVHTN6cKawuEwLS0tWlMCram+vp5AIHAmHwtPyVhrPU0gfZMxZgmQEW0wLAQuAcLW2hXGmGVAJZGGxghr7aeMMd8A9gFvAt+01s42xswGNgG3cXJj5C6gBNgFXEekeRIEXrfWrjLG/AmYYa095Z2tjDEbrbWTot//oOdrgauBD0bX8JK1dmJv+3Ueo/t8Pf30dz+1X9zxxXP5VYr0GQNTBnKk/YjfZYh4ohyLC5Tj+NPzqTQrVqzgd7/7HStWrOC6667jzTffZMWKFVx00UXMmzePkpISysrKeOutt7j99tvZunUrDz/8MGPGjOGOO+7waRWx19bWRlqa7sUn8a0zx+Xl5a+VlpZefS5z6FIadw0HtkW/XwW8D/hT9OetwIjo97+Mfn0bSAHKgd3GmOeBacDRHvOmR79WWWubgQogDBjg/cA/Re/1kUHk7JQz1dtr1wN/b4wZAWw/zX7vKSsp6yxKEembSvNL/S5BxDPlWFygHMenlStXsnr1aiBys8ZPf/rTVFRUAPD6669z8cUXc9VVV7F161YAdu/ezaWXXgrAqFGjePfdd1m0aJE/xZ8nVVVVfpcg4lkscqxLady1l8gZHeuJXDKzF/gQ8GL06x4iTYWWHq+7Ethsrf26MeY3RC6zaQc672gzncglM715E/gva+0GY8xngbO52Ouk11prO4wx1cCNwFNejnHs+LGzKEWkb+o8dVkkninH4gLlOD4tWLCAhQsX8thjjzFixAhuvvlmFi9ezNNPP00oFGLVqlVkZmYyc+ZMKisrefHFF3nhhRcAePjhh1m0aBH9+/f3eRWx1XnJg0g8i0WO1Rhx10+BX0TPrKgFbgZ+bIzZBLwDfItIw6SnA8C3jTH3AG1EztSoAv7NGFManetU/gV41BizHPgrsPos6j3Va9cCPwC+GYNjiIiIiEiCGjBgAGvXnvjve6tWrTppv7KyMjZs2MCSJUvIzs4G4O67774QJYqIT9QYcZS1thW4ocfmG3v8vKzb/qu6bZ/WY78gMKHHtlXR102K/nxT9OvMs6hxUrfvK3t7rbX2WeDZ99qv53w9pfZLPdOyRPqsof2H8mrwVb/LEPFEORYXKMduGzBgAJ/4xCf8LuOCaG5uJj8/3+8yRDyJRY5181U5b4wxxZx8Rseb1tovXehaNm/ebEeOHHmhDysSU7pBmrhAORYXKMfiCmVZXKCbr0qfZq2ttNZO6vHngjdFADo6Ovw4rEhMVVdX+12CiGfKsbhAORZXKMvigljkWI0REZE4YYzxuwQRz5RjcYFyLK5QlsUFscixGiOSEJKTdTsdiX95eXl+lyDimXIsLlCOxRXKsrggFjlWY0QSQigU8rsEEc90uqu4QDkWFyjH4gplWVygS2lEzlBSUpLfJYh41vnIQJF4phyLC5RjcYWyLC6IRY7VGBERiRPhcNjvEkQ8U47FBcqxuEJZFhfEIsdqjEhC0H/0xQUtLS1+lyDimXIsLlCOxRXKsrggFjlWY0QSQiAQ8LsEEc+Ki4v9LkHEM+VYXKAciyuUZXFBLHKsxogkBN18VVxQWVnpdwkininH4gLlWFyhLIsLYpFjNUYkIegZ7eICnfkkLlCOxQXKsbhCWRYXxCLHyTGoQ6TP2xfcx6SHJvldhogng9MGU9FW4XcZIp4ox+IC5bhvqVtS53cJcSsnJ8fvEkQ8i0WOdcaIJISMpAy/SxDxbHzueL9LEPFMORYXKMd9T319PRs2bKC2ttbvUuJKTU2N3yWIeBaLHOuMEUkIrcdb/S5BxLNdTbv8LkHEM+VYXKAc9y0NDQ3Mnz+fqVOncu+99/Jf//VfTJ48mSFDhgDw7W9/m2HDhjFmzJgTtm3dupW1a9cCEAwGGTt2LN///vd9WoU/dMaIuCAWOVZjpA8wxiwDNlprN57j639grb0tpkWdWx1DgCHnug4Px30YGAmkA5+21h7ouU+yUdQl/uUF8vwuQcQz5VhcoBz3LXv27GH58uWUlJTQ0NDAr3/9a+bNm8eyZcu69tm5c+dJ20aOHMnNN98MwF133cX8+fMvcOX+a29v97sEEc9ikWNdSuOAvtAUiRoCTLqQBzTGfBA4Yq0tBVYCS3rbL2B0YymJf4PSBvldgohnyrG4QDnuW6655hpKSkrYsmUL5eXlpKWlsW7dOq677joWL15MR0cH27dvP2lbp0OHDnHkyBHGjBnj4yr80dqqs6ol/sUix/pn9L7jdmPM/cBh4AUgbK1dZYyZRKTZcD/wS2AwEALmWmuDAMaYjdbaSdHvbwKujP4pBm4A9gA/AYYB1cCngOM95wMaezuGMWYj8F/AQmvtFcaYJOCx6H41wCeBRcBCYEC05uujYycc11ob7rnwaM0Loj+2Azd0O+4jwN3AVGttZfR3VAq0RPcrB8qjry0EjvT2y21paiHvZ3k0h5tJT0pn2LXD2D9yP9MKpnGg9QBt4TaGZw5nU90mSnJKCJgAL9W/RGl+KfuO7gNgaP+hrK9dz8TciYRsiFeDrzIhbwJ7m/eSlpTGkPQhrKtZx7SCaTR2NLK7aTfjc8ezq2kXeYE8BqUN6hqvC9Wxr2Uf4waMY0fjDi5KvYii1KKu8apjVRw6dogx2WPY1rCNoRlDyQvkdY0fbDtIXaiO0Vmj2VK/hVFZo8hOzu4a15rcXFPABJgzcI5Ta3LxfdKaTr+m9H7pDM8Y7tSaXHyftKbTrym9Xzp5gTyn1hTP71NFRQVpaWmsXr2alJQU/u7v/o4f//jHDBgwgBUrVvDrX/+ayy67jFWrVpGWlsby5ct5/PHHmTRpEoWFhTz44IN88pOfpLa2lubmZoqKiqiursYYQ15eHtXV1WRnZxMOh2lpaaG4uJjKykoCgQA5OTnU1NSQk5NDe3s7ra2tXeMpKSlkZWVRW1tLbm4ura2ttLW1dY2npaWRnp5OfX09+fn5NDU10d7e3jWenp5OSkoKwWCQgoICgsEgoVCoazwjI4OkpCQaGxspLCykrq4Oay2FhYVUVVWRmZkJcNo1paSkUFFR4dSaXHyftKbTrykcDlNVVdXbx8AzZqy1niYQ76KX0hy31v6zMeYR4H+Bhh6NkYeBPwBXAROBv1hr346+vmdj5B+BycCNwMXAG8Aca+1NxpgHgY3A5p7zEWk2nHQMY8ybwL9ba38QPcZA4KPAE8DPgR9aa//UWau1dll0vzk9j2ut/V0v678JGG+t/aIx5qvR38W/RhsjW4G7rbXWGHMV8H1r7WRjzBIAa+1D0TlygZeixz/p1uSrn1ltb9x+4xm+IyJ9043vu5HHDz/udxkinijH4gLluG/p/lSaFStWMGLECObOnQvAI488QigU4gtf+AKpqaknbPvyl7/M8ePHmT59OuvWrcMY40v9fqqoqGDw4MF+lyHiSWeOy8vLXystLb36XObQpTR9x5+iX8uBpG7b0wGstbXAKuA5ImdmNJ1mrsettSHgbSAFeD/w4WijYQJQ1Nt8pzlGEHio2/wh4OPAGuDyzhp7cdJxT1Pza9Gv/0PkkpxOy+3funfvBy6PzvdpIB/ARP4v9ihwb29NEYDwySeqiMSdupAeRyjxTzkWFyjHfcvKlStZvXo1AI2NjSxdupTdu3cTDod59tlnGTVqFLfeeutJ2wBeeeUVxo4dm5BNEYCUlBS/SxDxLBY5VmOk7xgb/XoFUEnkshCAjwEYYy4Baq2104CDRC59OZWWHj+/CayOnlVyG/BGb/Od5hhHrbXHu803F9gd/Xqw2/ZWoH+0XtPbcU9T87jo1zHAvs6N1trmHuvoPDvmH4Ft0e3fAnb1djZKp2PHj53m0CLxYV/LvvfeSaSPU47FBcpx37JgwQKeeOIJZs6cSTgc5plnnuHWW29lwoQJlJSUMGnSJL761a+etA3gD3/4A+PHJ+7jl7OysvwuQcSzWORY9xjpO641xrxE5F4cLwG/iT7lpVMlMMsY8yUiZ5Q8chZz/w6YGZ3fAp8FqnqZ70yPsRl4EphBpBnSeQeyHcDXjTF/BH4U3afncU/lEmPMBqCNyH1RTmKtfd0Y8050vhTgS8aYEcCdwMvRM0lesdbe3fO1/ZP6n+bQIvFh3IBx7G/d73cZIp4ox+IC5bhvGTBgQNdjdzu9/PLLJ/w8cuTIk7YB3Hfffee1tr6utra2634QIvEqFjnWPUbEd9F7jGCtXXW+jvHyyy/bD3zgA+drepELorGxkezsbL/LEPFEORYXKMfiCmVZXNCZYy/3GNEZI3JBGWNWE3laTncfs9ae12eFHT9+/L13EunjWltb9ZcXiXvKsbhAORZXKMvigljkWI0RuaCstfP9OK4aI+KCtrY2v0sQ8Uw5Fhcox+IKZVlcEIsc6+arkhACgYDfJYh4Vlzc82QrkfijHIsLlGNxhbIsLohFjtUYkYQQCoX8LkHEs8rKSr9LEPFMORYXKMfiCmVZXBCLHKsxIgmhXz9FXeJfWlqa3yWIeKYciwuUY3GFsiwuiEWO9WlREoIaI+KC9PR0v0sQ8Uw5Fhcox+IKZVlcEIsc69OiJISOjg6/SxDxrL6+3u8SRDxTjsUFyrG4QlkWF8Qix2qMSEJITtYDmCT+5efn+12CiGfKsbhAORZXKMvigljkWI0RSQh6XK+4oKmpye8SRDxTjsUFyrG4QlkWF8Qix2qMSEJQY0Rc0N7e7ncJIp4px+IC5VhcoSyLC2KRY11fIAnhz8E/M/mhyX6XIeJJXiCPulCd32WIeKIciwviMcd1S+KrXrkwiouL/S5BxLNY5FhnjEhCyE7O9rsEEc+mFUzzuwQRz5RjcUE857i+vp4NGzZQW1vrdynSB1RWVvpdgohnscixGiOSEEI25HcJIp4dbDvodwkininH4oJ4zXFDQwPz58+nvLyc2bNn884773D99dczd+5cPve5z9He3k5HRwejR49m1qxZzJo1izfeeIPGxsaT9hM36HG94gI9rlfkDHVYPa5X4l+8nbYt0hvlWFwQrznes2cPy5cvZ+nSpUyZMoVnnnmGRYsW8fTTTzNw4EDWr1/Pnj17mDdvHmVlZZSVlTFy5EjWrFlz0n7ihpSUFL9LEPEsFjlWY0ROYoz5gd81dDLG/MwYs9EYc7+XedL7qRsu8W901mi/SxDxTDkWF8Rrjq+55hpKSkrYsmUL5eXlfPrTn2by5Mg92GpqaigoKGD79u2sW7eO6667jsWLF9PR0cEtt9xy0n7ihmAw6HcJIp7FIsdqjMhJrLW3+V1DN39nrZ1krf2ml0lawi2xqkfEN1vqt/hdgohnyrG4IJ5zbK1l7dq1DBgwgEAgAMC2bdsIBoOUlJQwZswY1q5dy4svvkhHRwcvvPBC12u77yduUJNLXBCLHOupNAnCGLMM+HugP1ANzAdeBP4LWGitvaLbvhuttZOi3xvgh8BVQCj6uirgJ8Cw6FyfstaGeznmTcCC6I/twA3W2qAxZiPwCHA3MNVaWxk9I6QUaAFuiB7vfmB0dP8V1toXeu53qvl61pLSmkLez/JoDjeTnpTOsGuHsX/kfqYVTONA6wHawm0MzxzOprpNlOSUEDABXqp/idL8UvYd3QfA0P5DWV+7nom5EwnZEK8GX2VC3gT2Nu8lLSmNIelDWFezjmkF02jsaGR3027G545nV9Mu8gJ5DEob1DVeF6pjX8s+xg0Yx47GHVyUehFFqUVd41XHqjh07BBjssewrWEbQzOGkhfI6xo/2HaQulAdo7NGs6V+C6OyRpGdnN01rjW5uabPXfQ5djfvdmpNLr5PWtPp1/SZiz7Dk5VPOrUmF98nren0axqbPZYfvv3DuFpTRUUFxcXFVFZW8tWvfpUf/vCHPPbYY8yYMYPbb7+d7373uxw7doysrCySk5Opr6/n0ksvZe/evYwePZqGhgbuvPNOHnjgga4btzY3N1NUVER1dTXGGPLy8qiuriY7O5twOExLS0vXMQOBADk5OdTU1JCTk0N7ezutra1d4ykpKWRlZVFbW0tubi6tra20tbV1jaelpZGenk59fT35+fk0NTXR3t7eNZ6enk5KSgrBYJCCggKCwSChUKhrPCMjg6SkJBobGyksLKSurg5rLYWFhVRVVZGZmZmQa6quriY1NdWpNbn4PmlNp1/TX//6VwoLC3t+BDwrxlrraQKJD9HGSLu19lvGmB8BfwC+Bfy7tfYHPfbt3hiZDcy01n7JGPNxwAIBYI619iZjzIPARmvt73o55k3AeGvtF40xXwWOW2v/NdrI2Arcba21xpirgO9baycbY5YAWGsf6qWWXvfrOV9v61/9zGp74/Ybz/G3J9I33Pi+G3n88ON+lyHiiXIsLojHHNctqWPlypUUFRUxf/587rrrLqZOncrDDz/M//t//6/rUpmFCxeydOlSRowYwdy5c/nKV77C+PHjueGGG07YT9xQUVHB4MGD/S5DxJPOHJeXl79WWlp69bnMoUtpEstr0a//AwwBgsBD7/Ga4cA2AGvt74H/Bt4PfDjakJgAFJ3FMTst79bEeD9weXS+TwP5p5jrdPstP1VTBKCxo/E0JYrEh3U16/wuQcQz5VhcEK85XrBgAU888QQzZ84kHA5TUVHBzp07efDBB5k1axZPP/00X/3qV7n11luZMGECJSUlTJo0iV/96lcn7SduKC4u9rsEEc9ikWNdSpNYxgHrgDFEGhxHrbXH3+M1e4EZwKPGmM8AI4FXgdXW2m8aYz5C5CyS0x3zkegx93VutNY2d9vnTSJnnSwwxowCTtW2PuV+PeY7SXZy9umGReLCtIJpcfcvlCI9KcfignjN8YABA1i7du0J226++eaT9nv55ZdP2qe3/ST+VVZW6owRiXuxyLEaI4mlJHq2RSXwe+ArZ/CaMuBjxphNwFHgc0AtMNMY8xKRpshnT/P6S4wxG4A2IvcOOYm19nVjzDvR+VKAL3nZrzfttv1MdxXpsw60HvC7BBHPlGNxgXIsrsjIyPC7BBHPYpFjNUYSy4PW2o3dfp7U206d9/SIfm+Bf+plty+c4TF/Y61ddar5u227971qOdV+vc3X02U5l1G3pO69dhPp0+rr68nNzfW7DBFPlGNxgXIsrkhKSvK7BBHPYpFjNUYShLV22fmc3xizGuh5cdfHrLWt5/O4ZyocPumhOSJxp7GxUX8Rl7inHIsLlGNxhbIsLohFjtUYkZiw1s73u4bTCQQCfpcg4pnXx5CJ9AXKsbhAORZXKMvigljkWE+lkYTQ0dHhdwkintXV6XIwiX/KsbhAORZXKMvigljkWI0REZE4cZonUovEDeVY739MCgAAIABJREFUXKAciyuUZXFBLHKsxogkhORkXTUm8U+nu4oLlGNxgXIsrlCWxQW6lEbkDIVCIb9LEPGsqqrK7xJEPFOOxQXKsbhCWRYXxCLHaoxIQtCjyMQFmZmZfpcg4plyLC5QjsUVyrK4IBY5VmNERERERERERBKWGiOSEMLhsN8liHjW3NzsdwkininH4gLlWFyhLIsLYpFjNUYkIQQCAb9LEPGsqKjI7xJEPFOOxQXKsbhCWRYXxCLHelSHJIR3Gt7hIw99xO8yRDy5vuh61lSt8bsMEU/iKcd1S+r8LkH6qOrqai655BK/yxDxTFkWF8QixzpjRBKCRc9ol/gXsnq6ksQ/5VhcYIzxuwSRmFCWxQWxyLEaI5IQWsItfpcg/z979x4fZXnn//91ESYkhEzIkJAUPLAt9YgVVuMqbTmlSxQ3rZXioa1W6O66v1T8Qct+W3e1P7pb3d3H+nOtrN0etlRbf6vWLramtUUFgSqyUGEVVKxhl1SICTnOZEKSmSTX748M0xDCQe4bbuaa9/Px4JG557rv6/pcM+8Hmov7IJ5ti24LugQRz5RjcUEkEgm6BBFfKMviAj9yrIUR8ZUxZqUxZs4J7DfdGDP9BPvc4LWucTl6FJlkvlmRWUGXIOJZpuU4FouxaNEirr/+em655ZYjthOJRHrfAwcOMHv27PT20qVLmT9/Pvfff38Qpcsp1NzcHHQJIr5QlsUFfuRYCyMSlOmpP6dFz0DP6RpK5JTZHd8ddAkinmVajp966ilqampYs2YNEydO5PHHHz9se926del9v/71r9PTM/jfm9raWgYGBnjuuefYu3cve/bsCWoKcgqEw+GgSxDxhbIsLvAjx7r5qpwKf2qM+TsgDHwK+EdgErAPWAx8A/g0gDHmFmttpTFmLPAjYCKw01r7pZE6NsasBDZYazcYY25LvT0ZeMNa+zNjzF1AnbX2sDv7mYOGyOoI8f44+Tn5nPfx89hz0R6qSqrY272Xnv4eLhh3AZvaNlFRVEHIhNjYvpHKCZXUHawDYOrYqaxrXcfs4tkkbZJt0W3Misxid3w3eTl5TMmfwtqWtVSVVBHri7Grcxczi2eys3MnkVCEyXmT0+1tyTbquuq4YvwV7IjtYNKYSZSNKUu3N/U20dDbwIzwDLZ2bGVqwVQioUi6fX/PftqSbVxSeAmb2zczrXAa4dHhdLvm5Oac5k6Yy7n55zo1Jxe/J83p2HP6RMkn6B7ozog5NTQ0cNNNN9HS0kJHRwf79+9nzpw5zJw5k/r6evbt20dBQQH19fW89dZbGGMIh8P09vbyq1/9ijlz5hCLxbjkkkvYuHEjY8eOJZFIUF5eTmNjI/n5+eTm5hKNRikpKSEajZJMJtPtBQUF5OTkEIvFKC0tpa2tDWstpaWlNDU1MW7c4NmQ8XicsrIympubMcYQiURobm4mHA7T399PV1dXus9QKERRUREtLS0UFRWRSCTo7u5Ot+fm5lJYWEhrayvFxcV0d3fT09OTbs/LyyM/P5/29nYmTJhAZ2dnVs4pGo0yduxYp+bk4vekOR1/Tu3t7cRiMafm5OL3pDkdf05Dz+A8GcZa3ZRS/JNauLjQWnujMebrqbf7rbX3ptoarbXfObSoYa19JHXcMmC8tXalMWYNsNJa+3qqbYO1ds6Q/ocvjGwGvmKtvd0Y8yvgM9baw24q8sQvn7A3//bmUzVtkdPi5g/czOPvPR50GSKeZFKOhz6VZuvWrdx333387Gc/O2I7kUjwmc98hh//+Md8/vOfp7a2lqVLl3L77bczbdo01q9fz+uvv86yZcuCmor4rL6+nnPPPTfoMkQ8U5bFBYdyvH379lcrKysvP5k+dMaInAo/Sv38PfBt4JOp7S3ANUc55nxgZur+JOMZPAvk9eOMkw90W2t/Z4w5yxgTBjqGL4oAxPpi728GImegtS1rgy5BxLNMzHF7eztf+9rXePTRR0fcfvDBB1myZAlFRUXpYwoKCuju7gagq6uLgYGB01+4nDLl5eVBlyDiC2VZXOBHjnWPETkVhi5M/DVwZer1lcAbqdfdwFgAM/h8pbeBB1NnhtzN4KLKSBJAaer11UPe3wosA54Z6aDwaF0/KZmvqqQq6BJEPMu0HCcSCRYvXsw999zD2WeffcQ2wMaNG/nBD35AdXU1O3fu5M4772T69Ols2bIFgF27dnHOOecEOQ3xWWNjY9AliPhCWRYX+JFjnTEip1ofcLExZhPwLnBf6v3ngZ8YYz4H3AV8H/ihMWYxEAM+e5T+ngG+bYypBFqHvP8U8BIw4rmAA+hf6iTz6cwncUGm5fixxx7jtdde44EHHuCBBx7gYx/72GHbixcv5pe//GV6/+rqah566CFisRjXXnstjY2NvPDCCzz//PMBzkL8FgqFgi5BxBfKsrjAjxzrHiOSFX7wzA/sn+/486DLEPHk3Lxzqe+pD7oMEU8yKcdD7zFyMjo6OnjxxReZOXMmZWVlPlUlZ4Kuri4KCgqCLkPEM2VZXHAox7rHiMhxfCj8Ic//gysSNN0gTVyQTTkeP348n/70p4MuQ06BlpYW/TIpTlCWxQV+5Fj3GJGskJOTE3QJIp4NvbGjSKZSjsUFyrG4QlkWF/iRYy2MSFbQJWPiAq/PZxc5EyjH4gLlWFyhLIsL/MixFkYkK+gxieKCQ4/+FMlkyrG4QDkWVyjL4gI/cqyFEckKuuO2uMCPZ7SLBE05Fhcox+IKZVlc4EeOtTAiWSGZTAZdgohnfjyjXSRoyrG4QDkWVyjL4gI/cqyFEckKo0Yp6pL5cnNzgy5BxDPlWFygHIsrlGVxgR851m+LkhW0MCIuKCwsDLoEEc+UY3GBciyuUJbFBX7kWL8tSlbo6+sLugQRz1pbW4MuQcQz5VhcoByLK5RlcYEfOdbCiGSF0aNHB12CiGfFxcVBlyDimXIsLlCOxRXKsrjAjxxrYUSygh7XKy7QI/XEBcqxuEA5Flcoy+ICP3Ksf0aXrNDQ2cDsh2YHXYaIJzd/4GYef+/xoMsQ8SQTctx2Z1vQJcgZrqenJ+gSRHyhLIsL/MixzhiRrBDriwVdgohna1vWBl2CiGfKsbigvLw86BJEfKEsiwv8yLEWRuSEGGOmG2OmBzBujjGm1hjzojHm/zrZfsKjw36WJRKIqpKqoEsQ8SxTchyLxVi0aBHXX389t9xyyxHbiURixPfq6+u58cYbWbBgAXfffXfQ05BTpLGxMegSRHyhLIsL/MixFkbkRE1P/TndJgNRa+1ca+2/nWwnfVZPpZHM19TbFHQJIp5lSo6feuopampqWLNmDRMnTuTxxx8/bHvdunVH7LNu3TpWrlzJihUrePbZZ2loaOCll14KeipyCuTl5QVdgogvlGVxgR851j1G5AjGmHzgKSAMtAK7gU+n2m6x1lYaY8YBPwUKgDpr7eJU+wZgG/ARa22VMWYl8CfAWKAZuMla25fa7+fAYmvtR4wxBvgecF5qvxuBzwDLgSmp/ZcCu4bvZ63tH97f8DklbdLPj0gkEA29DUGXIOJZpuT4i1/8Yvp1S0sLN910ExUVFentkpISrrnmmsP2KSkpYc+ePVx66aUAlJaWEovpUk4X5efnB12CiC+UZXGBHznWwoiM5CJgwFo7yxjzSWAT8DaAtfaR1D4fAFYBLwC/NsaUWWubgCuBh6y1fz2kv99Ya+8zxjwMfAr4z9TxdsgixqeAkLV2tjHmAeBaa+2Txpj/AlZaa28DMMZcN3w/4JkR+jtMqDtEZHWEeH+c/Jx8zvv4eey5aA9VJVXs7d5LT38PF4y7gE1tm6goqiBkQmxs30jlhErqDtYBMHXsVNa1rmN28WySNsm26DZmRWaxO76bvJw8puRPYW3LWqpKqoj1xdjVuYuZxTPZ2bmTSCjC5LzJ6fa2ZBt1XXVcMf4KdsR2MGnMJMrGlKXbm3qbaOhtYEZ4Bls7tjK1YCqRUCTdvr9nP23JNi4pvITN7ZuZVjiN8Ohwul1zcnNOn/vA53g19qpTc3Lxe9Kcjj2nWybdwo8bfnxGz6m3t5fGxkZCoRB1dXU0NTXx4Q9/mAMHDrBlyxba29uZOHEi7733HoWFhaxfv57W1lbOOeccZs2axX333ccHP/hB1q5dy7Jly6ivr2fChAl0dnaSSCQoLy+nsbGR/Px8cnNziUajlJSUEI1GSSaT6faCggJycnKIxWKUlpbS1taGtZbS0lKampoYN24cAPF4nLKyMpqbmzHGEIlEaG5uJhwO09/fT1dXV7rPUChEUVERLS0tFBUVkUgk6O7uTrfn5uZSWFhIa2srxcXFdHd309PTk27Py8sjPz+f9vb2rJ5TS0sL559/vlNzcvF70pyOP6fGxkba29udmpOL35PmdOw57d27l7KyspF+DTxhxlrrqQNxT+rsjXuBy4F3GDxr47Pwh4URY8wU4F+AfuDDwKestXuNMb+11l4+pK+VwCvW2rXGmNuBcdba/9cYsxW40lo7kNrvq8AS4D1gHPBda+33U+MMXRg52n6H9Tfc6mdW2y/u+OJITSIZ40P5H2JP956gyxDxJBNyfOipNO3t7SxcuJBHH32Us88++4jtkfYB2LJlC6tWrWLGjBmsWLEisHnIqROPx9P/4y+SyZRlccGhHG/fvv3VysrKy49/xJF0jxEZyaXAy9ba+UAx8HGgm8HLYQ4tnHyRwUtpbga6hhwbH6G/K1I/ZwB1qdcHhy1ivA08Ya2dAywD3jxKbUfbb3h/hxkzaszRmkQyxtSCqUGXIOJZpuQ4kUiwePFi7rnnHs4+++wjtkfa55Bp06axb98+ampqgipfTrHOzs6gSxDxhbIsLvAjx1oYkZHsBe40xmwGyoHfAs8D1xtjXmZwoeR54C5gfeqYycforyJ1D5DxwC+Oss8zwCRjzEbgm0C9x/0Ok2NyTmQ3kTNaJBQJugQRzzIlx4899hivvfYaDzzwANXV1fzLv/zLYdtr1qw5Yp81a9YAsGrVKmpqahg7dmzAs5BTJZFIBF2CiC+UZXGBHznWpTRySqUupdlgrd0QZB3f+/n37O3/fXuQJYh4FglFaEu2BV2GiCeZkONDl9KIHE1vby9jxuhsVMl8yrK44FCOdSmNnLGstSuDXhQBCI8OB12CiGdVJVVBlyDimXIsLmhsbAy6BBFfKMviAj9yrKfSSFaYVDhJ/wIoGe/AgQM8PPHhoMsQ8UQ5FhfoEafiCmVZXOBHjnXGiGSFwfvFimS23NzcoEsQ8Uw5Fhcox+IKZVlc4EeOtTAiWaG/vz/oEkQ8i0ajQZcg4plyLC5QjsUVyrK4wI8ca2FEssLo0bpqTDJfSUlJ0CWIeKYciwuUY3GFsiwu8CPHWhiRrKAzRsQF+lcdcYFyLC5QjsUVyrK4QGeMiJwgPZZaXJBMJoMuQcQz5VhcoByLK5RlcYEfOdbCiGSFUCgUdAkinpWXlwddgohnyrG4QDkWVyjL4gI/cqyFEckKWg0XF/jxjHaRoCnH4gLlWFyhLIsL/MixFkYkK+Tk5ARdgohnBQUFQZcg4plyLC5QjsUVyrK4wI8ca2FERCRDaIFPXKAciwuUY3GFsiwu8CPHWhiRrKCn0ogLYrFY0CWIeKYciwuUY3GFsiwu8CPHo32oQ+SMVxerY+5Dc4MuQ8STyWMms793f9BliJywtjvbjnivtLQ0gEpE/KUciyuUZXGBHznWGSOSFQpydP2kZL6KooqgSxDxrK3tyMUSkUyjHIsrlGVxgR851sKIZAWDCboEEc9CRo+dlsx04MABFixYAMC7777LjTfeyIIFC7j77rsBWL16NdXV1VRXVzNr1iyWL18OwNKlS5k/fz73339/YLWLjMRaG3QJIr5QlsUFfuRYCyMOM8Y8GHQNxzK8PmPMFGPMnOPtdzI6+zu9diESuI3tG4MuQeR96+jooKamhoMHDwLwne98hxUrVvDss8/S0NDASy+9xJIlS6itraW2tparrrqKW2+9ldraWgYGBnjuuefYu3cve/bsCXgmIn+gyw/EFcqyuECX0sgxWWuXBV3DsYxQ3xRgzgns974V5hR67UIkcJUTKoMuQeR9GzVqFKtXr6awcPDv4bfffptLL70UGPwfmaE3TGtoaODAgQPMmDGDl19+meuuuw6AuXPnsmXLltNfvMhRNDU1BV2CiC+UZXGBHznWzVczjDFmJfAnwFigGbgJeAH4ObDYWvuRIftusNbOSb02wL8C04Fk6rgm4HvAeam+brTWHvH4ltSxPwLOTR17PRAbfixwC3Bp6k85cAPwxvBjrbXREer7v4HFwPjUWSOLrLXNI+z3OaDUWvugMeZm4Czg/uPNozfeS2R1hHh/nPycfM77+HnsuWgPVSVV7O3eS09/DxeMu4BNbZuoKKogZEJsbN9I5YRK6g7WATB17FTWta5jdvFskjbJtug2ZkVmsTu+m7ycPKbkT2Fty1qqSqqI9cXY1bmLmcUz2dm5k0gowuS8yen2tmQbdV11XDH+CnbEdjBpzCTKxpSl25t6m2jobWBGeAZbO7YytWAqkVAk3b6/Zz9tyTYuKbyEze2bmVY4jfDocLpdc3JzTmW5ZVw38Tqn5uTi96Q5/WFO9fX1lJeX09jYSCKRIB6PM3v2bP7+7/+eiy++mF//+td89atfpb6+nry8PL797W9z7bXXEo/HaWlpwVpLb28vyWSS//3f/6Wjo4NoNEpJSQnRaJRkMpnuv6CggJycHGKxGKWlpbS1tWGtpbS0lKamJsaNGwdAPB6nrKyM5uZmjDFEIhGam5sJh8P09/fT1dWV7jMUClFUVERLSwtFRUUkEgm6u7vT7bm5uRQWFtLa2kpxcTHd3d309PSk2/Py8sjPz6e9vZ0JEybQ2dlJIpFIt+fn55Obm6s5ZeCcuru76e3tdWpOLn5PmtPx5zQwMHDY39UuzMnF70lzOvacuru7PS+OGF1XlllSCyMJa+19xpiHgfXAfcC/WWuHX5oydEHhk8C11trbjTF/BlggBFxnrb3NGPMAsMFa+8wIY05IjTMdmA38D/DHw48FIsCfA3OBQ4sW3x1+rLX298PrS23PAeZYa1ceYx5h4DFr7SeNMY8A32BwIeaY83i09lF72/bbjvv5ipzJKooq2BbdFnQZIids6FNpqqurqa2tpbW1lXfeeYdVq1YxY8YMVqxYAcDAwABXX301a9euxRjD1772NRYuXEhFRQW1tbW88847fPnLXw5qKiKHaW1tZcKECUGXIeKZsiwuOJTj7du3v1pZWXn5yfShS2ky06upn68zePlJFHjoOMdcAGwFsNb+AvgVcD5wlTFmAzALKBvpQGttK/AI8GsGz+roPMaxj1trk8DvgdyjHHvSrLUxoNcYMw4osdb+74nMY8yoMV6GFTkjTB07NegSRDyLx+NMmzaNffv2UVNTk37/lVde4bLLLmPwJEWYPn16+vKZXbt2cc455wRSr8hI4vF40CWI+EJZFhf4kWMtjGSmK1I/ZwB1wEFr7cBxjtkNVED6cpS/B94GnkidjbEMeHOkA40xZwOt1toqYD+Dl9Ic7diuEzj2aLoZvETo0OU7R/ML4MvAy6nt485DN18VF6xrXRd0CSKelZWVsWrVKmpqahg7dmz6/fXr1zNz5sz09oIFC/jJT37C3/7t3/Kzn/2M+fPnB1GuyIjKykb8tySRjKMsiwv8yLEWRjJTRersiPEMLhKciFrAGmM2MXgvkAeBZ4BJxpiNwDeB+qMc2whUG2NeBuYxeE8TL8cezQ7gfGPMbxi8Z8nR/JzBhZGfpraPW4tuvioumF08O+gSRE5abW0tAM3Nzdx1113ceOPhf83fc889VFdXp7fD4TC1tbVcfvnlPPPMM4TD4dNar8ixNDc3B12CiC+UZXGBHznWPUYyTOoeIxustRsCLiWjbNy40X7kIx85/o4iZ7B9+/Zx1llnBV2GiCfKsbhAORZXKMvigkM59nKPET2VJsMMvzGp34wxTzD4RJmhrrHWdp/KcU+10aMVdcl8kUgk6BJEPFOOxQXKsbhCWRYX+JFjXUojh7HW3mStnTPsT0YvigAkk8mgSxDxTKe7iguUY3GBciyuUJbFBX7kWAsjkhVycnKCLkHEM91jQVygHIsLlGNxhbIsLvAjx1oYERHJEP39/UGXIOKZciwuUI7FFcqyuMCPHGthRLKC/tIXF3R1dR1/J5EznHIsLlCOxRXKsrjAjxxrYUSyQigUCroEEc/Ky4ffF1kk8yjH4gLlWFyhLIsL/MixFkYkK+jmq+KCxsbGoEsQ8Uw5Fhcox+IKZVlc4EeOtTAiWcEYE3QJIp7pzCdxgXIsLlCOxRXKsrjAjxxrYUSygp5KIy4oKioKugQRz5RjcYFyLK5QlsUFfuRYCyOSFfr6+oIuQcSzlpaWoEsQ8Uw5Fhcox+IKZVlc4EeOR/tQh8gZ7387/5e5D80NugwRT6aNm8au+K6gyxA5rrY7247apn+dFBcox+IKZVlcoDNGRE7QaKM1QMl8kVAk6BJEPEskEkGXIOKZciyuUJbFBX7kWAsjkhVCRjeWksw3OW9y0CWIeNbd3R10CSKeKcfiCmVZXOBHjrUwIoExxmw4yeOmG2Omv59jYn2xkxlK5IyytmVt0CWIvC8HDhxgwYIFANTX13PjjTdy++23c/fddx+234oVK/j1r3+d3l66dCnz58/n/vvvP631ipyo8vLyoEsQ8YWyLC7wI8daGJFMND3154SFR4dPUSkip09VSVXQJYicsI6ODmpqajh48CAAK1euZMWKFXz3u9+loaGBl156CYBXXnmFAwcOcPXVVwNQW1vLwMAAzz33HHv37mXPnj2BzUHkaBobG4MuQcQXyrK4wI8ca2FEjmCMyTPGPGGMeckY8wtjTNgY82tjzG+MMT9M7bPSGHOvMWaTMea/jTHlIxw3NvXnp6n9Hj7OuBuMMf9sjFmb2h43wrj/AHwN+JoxZl3qveOO0W/7/fyIRALRljz6DS1FzjSjRo1i9erVFBYWArBnzx4uvfRScnNzKS0tJRaLkUwmWbZsGWeffTbPPvssAC+//DLXXXcdAHPnzmXLli2BzUHkaHJzc4MuQcQXyrK4wI8c646UMpK/BF6z1t5kjFkMXAisAl4Afm2MKUvtN9VaO8sY83VgHlAy7LhpwExgl7V2pTFmjTHmI9ba148y7pXAQ9bav05tf2D4uNbau4wxbwNYax8ZUu8xx0jEE0RWR4j3x8nPyee8j5/Hnov2UFVSxd7uvfT093DBuAvY1LaJiqIKQibExvaNVE6opO5g3eBkx05lXes6ZhfPJmmTbItuY1ZkFrvju8nLyWNK/hTWtqylqqSKWF+MXZ27mFk8k52dO4mEIkzOm5xub0u2UddVxxXjr2BHbAeTxkyibExZur2pt4mG3gZmhGewtWMrUwumEglF0u37e/bTlmzjksJL2Ny+mWmF0wiPDqfbNSc35zQlbwrXTbzOqTm5+D1pTjPp6OggkUjQ3d3NwMAA9fX1zJ07l29+85tMmTKF559/nttvv52HH36YqVOncv311/PTn/6Uuro6mpqaKCoq4r333iOZTPLee+9RX19Pfn4+ubm5RKNRSkpKiEajJJNJysvLaWxspKCggJycHGKxGKWlpbS1tWGtpbS0lKamJsaNGwdAPB6nrKyM5uZmjDFEIhGam5sJh8P09/fT1dWV7jMUClFUVERLSwtFRUXpOR1qz83NpbCwkNbWVoqLi+nu7qanpyfdnpeXR35+Pu3t7UyYMIHOzk4SiUS6XXPK3Dl1dXXR29vr1Jxc/J40pxObU319vXNzcvF70pyOPqd4PE5TU9NRfsU8McZa66kDcY8x5tvAf1pr1xljDDAFeADoBz4MfAq4Ddhmrf2lMea21KFXDDsO4NsMLo60A+OBu6y1v0qNs8FaO2fIuL+11l4+ZHsK8C9Dx7XW7j003qGFEWPMvx1tjEOe+OUT9ubf3uzxkxEJ1s0fuJnH33s86DJEjmvo43qrq6upra0FYMuWLfzTP/0TH/3oR1mxYgX/5//8H+bPn88nPvEJ3n77be69914mTZrEwoULqaiooLa2lnfeeYcvf/nLQU1FZET19fWce+65QZch4pmyLC44lOPt27e/WllZefnxjziSLqWRkewGKlKv/wbYDPwUuBnoGrJf13GO+3PgbeDB1ALI3cDvjzFufNj2F48ybjcwFiC1AHPcMboHdMdtyXw7YjuCLkHEk2nTptHc3ExNTQ0Af/RHf0R9fT0A//3f/81ZZ53F9OnT05fP7Nq1i3POOSewekWOpri4OOgSRHyhLIsL/MixLqWRkXwfeDT11JhW4EYGz/z4q1T70Z4ZOvy4zwE5wA9Tl9bEgM++jzqeH2Hcvan3f2KM+RxwV2rcY46hx/WKCyaNmcTurt1BlyFy0latWsWtt97K2LFjAfj85z/P0qVLWbNmDclkkkceeYRx48Zx7bXX0tjYyAsvvMDzzz8fcNUiR+ru7iYc1o3dJfMpy+ICP3KsS2kkK+hSGnGBLqWRTDH0UprhTuS07Y6ODl588UVmzpxJWVnZMfcVCYIuPxBXKMviAj8updHCiGSFl19+2V500UVBlyHiSW9vL2PGjAm6DBFPlGNxgXIsrlCWxQWHcqx7jIgcRzKZDLoEEc/8eEa7SNCUY3GBciyuUJbFBX7kWAsjkhVGjVLUJfPl5eUFXYKIZ8qxuEA5Flcoy+ICP3Ks3xYlK2hhRFyQn58fdAkininH4gLlWFyhLIsL/MixfluUrNDX1xd0CSKetbe3B12CiGfKsbhAORZXKMviAj9yrIURyQqjR+vJ1JL5JkyYEHQJIp4px+IC5VhcoSyLC/zIsRZGJCsMDAwEXYKIZ52dnUGXIOKZciwuUI7FFcqyuMCPHGthRLKCFkbEBYlEIugSRDxTjsUFyrG4QlkWF/iv3F4yAAAgAElEQVSRYy2MSFYIhUJBlyDiWXl5edAliHimHIsLlGNxhbIsLvAjx1oYkayQTCaDLkHEMz+e0S4SNOVYXKAciyuUZXGBHznWwohkBT2uV1ygR+qJC5RjcYFyLK5QlsUFfuRYj+qQrLAnuofZD80OugwRT6aNm8au+K6gyxABoO3OtpM6Ljc31+dKRE4/5VhcoSyLC/zIsf4ZXbJC/iithkvmu6TwkqBLEPEsGo0GXYKIZ8qxuEJZFhf4kWMtjEhW6OrvCroEEc82t28OugSRIxw4cIAFCxYAUF9fz4033siCBQu4++67R9ynpKSEjo4ObrjhBubNm8fy5csDqVvEi5KSkqBLEPGFsiwu8CPHWhiRrJCfozNGJPNNK5wWdAkih+no6KCmpoaDBw8CsHLlSlasWMGzzz5LQ0MDL7300hH7RKNRnnzySRYtWsT69euJx+Ps2LEjyGmIvG/6V3ZxhbIsLtAZI3LSjDErjTFzMrX/9zvuKEVdHBAeHQ66BJHDjBo1itWrV1NYWAjAnj17uPTSSwEoLS0lFosdsU8ymSQSifDWW28RjUbZv38/kydPDmwOIidDT7sTVyjL4gI/cqybr0pW6OrsIrI6Qrw/Tn5OPud9/Dz2XLSHqpIq9nbvpae/hwvGXcCmtk1UFFUQMiE2tm+kckIldQfrAJg6dirrWtcxu3g2SZtkW3QbsyKz2B3fTV5OHlPyp7C2ZS1VJVXE+mLs6tzFzOKZ7OzcSSQUYXLe5HR7W7KNuq46rhh/BTtiO5g0ZhJlY8rS7U29TTT0NjAjPIOtHVuZWjCVSCiSbt/fs5+2ZBuXFF7C5vbNTCucRnh0ON2uObk5p5AJcd3E65yak4vfU7bMqaWlha6uLsrLy+np6aGhoYGrr76av/3bv+XKK6/kueee47bbbmPMmDE0NjaSSCSIx+P09/dz8cUX88wzz/BP//RPfOhDHyIWi2GtJT8/n/b2diZMmEBnZyeJRILy8nIaGxvJz88nNzeXaDRKSUkJ0WiUZDKZbi8oKCAnJ4dYLEZpaSltbW1YayktLaWpqYlx48YBEI/HKSsro7m5GWMMkUiE5uZmwuEw/f396Tk1NjYSCoUoKiqipaWFoqIiEokE3d3d6fbc3FwKCwtpbW2luLiY7u5uenp60u15eXmak6Nz6u/vp7e316k5ufg9aU7Hn1Nubi719fVOzcnF70lzOvac+vv7aWpq8vT7orHWeupAMocxphh4CsgBDHA/cAdQANRZaxcbY74BvGWtfcIYsxLYba19YoS+xgE/HXbs8P5XAh8F3rDW/swYcxdQB/xqhGNXAiHg40AYuBroAB4Bzkq9viE1/I+AicBOa+2XRhrXWrthaL1P/PIJe/Nvbz75D0/kDHDzB27m8fceD7oMEeDwp9JUV1dTW1sLwJYtW1i1ahUzZsxgxYoVR+xTX1/PP//zP3PfffcRDod5+OGHKSgo4LbbbjvdUxA5afX19Zx77rlBlyHimbIsLjiU4+3bt79aWVl5+cn0oesLsstfAr+w1s4FksAHgFXAJ4ApxpgyBhcdPpvavwr4+VH6GunY4f3D4ILFNanXs4Bnj3IswFRr7SxgDTAv1d9r1tqPAf8JTEu9tyu13weMMR85yriHSdjEiX1CImewvd17gy5B5LimTZvGvn37qKmpGbG9oKCAaDTKm2++SX9/P6+++irGmNNcpYg3BQUFQZcg4gtlWVzgR461MJJd/gh4LfX6twwuIvw58P8BESDfWrsHKEzdp2OXtbb7KH0dcewI/WOt/R1wljEmDHRYa7uOciwMLsoA/B7IBS4AtqbeewTYBpwPfNoYswH4IDB5pHGHG7ADR/1QRDJFT39P0CWIHNeqVauoqalh7NixI7bn5OSwbNkyli9fzpQpU2hvb2fhwoWnuUoRb3JycoIuQcQXyrK4wI8ca2Eku/weuDj1ejrwRQYvabkZGPo82yeA1fxhoWIkIx07vP9DtgLLgGeOcSzDXgPsBipSr/+GwcWUt4EHrbVzgLtTYx5t3LS8UXnHmIpIZrhg3AVBlyAyokOX0QDcdddd3HjjjUfdJxaLcdlll/HKK6/w7rvv8vTTT6evRRbJFLFYLOgSRHyhLIsL/MixFkayy/eAhamzLcLA88BdwPpU+6HHAvwUsMBLx+hrpGOH93/IUwwujPziGMeO5PvAH6f6+2Pgx6n3rjHGbAL+Cnj3GOOmxfvjx5iKSGbY1LYp6BJEPCstLQ26BBHPlGNxhbIsLvAjx3oqTRax1rYAc4e9/XdDN4wxFwM/BO6zx7gzr7V2E4P3/BhueP9Ya99k8JKZYx378pD2R4a8fwNHGum9I8Yd6sNFHz7sRoEimWjfvn2cddZZQZch4klbW9tRL7MRyRTKsbhCWRYX+JFjLYzIYay1bwBXDH0vdSbGUFFr7adOW1EiAoCeIiYuUI7FBcqxuEJZFhf4kWMtjMhxpe7nkdFGj1bUJfPpdFdxgXIsLlCOxRXKsrjAjxzrHiOSFZLJEZ/iK5JRmpqagi5BxDPlWFygHIsrlGVxgR851sKIZAU9ikxcoCd3iAuUY3GBciyuUJbFBX7kWAsjIiIiIiIiIpK1tDAiWaG/vz/oEkQ8i8f12GnJfMqxuEA5Flcoy+ICP3KshRHJCqFQKOgSRDwrKysLugQRz5RjcYFyLK5QlsUFfuRYCyOSFfr6+oIuQcSz5ubmoEsQ8Uw5Fhcox+IKZVlc4EeOtTAiIpIhjDFBlyDimXIsLlCOxRXKsrjAjxxrYUSywujRo4MuQcSzSCQSdAkininH4gLlWFyhLIsL/MixfluUrPBux7t87KGPBV2GiCc3f+BmHn/v8aDLkCzRdmfbKem3ubmZc88995T0LXK6KMfiCmVZXOBHjnXGiGSFnoGeoEsQ8Wx3fHfQJYicsPb2dl588UVaW1sPez8cDgdUkYh/lGNxhbIsLvAjx1oYkawwyijqkvnycvKCLkGy0IEDB1iwYAEAHR0d3HDDDcybN4/ly5cDsHr1aqqrq6murmbWrFksX76cjo4ObrrpJrZv384nP/lJWlpa0v3p8eniAuVYXKEsiwv8yLF+W3SAMWalMWbOCew33Rgz/QT73ODHmO933JNhjAkZY540xjxnjFlvjCkevk+uyT1Vw4ucNlPypwRdgmSZjo4OampqOHjwIABPPvkkixYtYv369cTjcXbs2MGSJUuora2ltraWq666iltvvZU33niDb37zm3zlK19h3rx5vPbaa+k+u7q6gpqOiG+UY3GFsiwu8CPHWhjJLtNTf1wb9xrg19ba+cBa4JbhO8T6YqdweJHTY23L2qBLkCwzatQoVq9eTWFhITB4c7O33nqLaDTK/v37mTx5cnrfhoYGDhw4wIwZM/joRz9KRUUFmzdvZvv27VRUVKT3Ky8vP+3zEPGbciyuUJbFBX7kWDdfdcefGmP+DggDnwL+EZgE7AMWA98APg1gjLnFWltpjBkL/AiYCOy01n7Jw5hXA+3AI8cbd6SOjDErgT8BxgLNwE3W2r7UmSs/BxZbaz9iBp/F9D3gvNR+N1prnxnSVSnw2+H9j+0dS2R1hHh/nPycfM77+HnsuWgPVSVV7O3eS09/DxeMu4BNbZuoKKogZEJsbN9I5YRK6g7WATB17FTWta5jdvFskjbJtug2ZkVmsTu+m7ycPKbkT2Fty1qqSqqI9cXY1bmLmcUz2dm5k0gowuS8yen2tmQbdV11XDH+CnbEdjBpzCTKxpSl25t6m2jobWBGeAZbO7YytWAqkVAk3b6/Zz9tyTYuKbyEze2bmVY4jfDocLpdc3JzTkvPWcqrsVedmpOL35Mrc2ptbSUej1NWVkZvby/79u3j0ksv5emnn+Zb3/oW55xzDrFYjKKiIhobG3n44Yf57Gc/S319PUVFRfT29vKjH/2IcDjMe++9R1dXF4WFhfzP//wPU6ZMobu7m56eHsrLy2lsbCQvL4/8/Hza29uZMGECnZ2dJBKJdHt+fj65ublEo1FKSkqIRqMkk8l0e0FBATk5OcRiMUpLS2lra8NaS2lpKU1NTYwbNw4gPafm5maMMUQiEZqbmwmHw/T399PV1ZXuMxQKUVRUREtLC0VFRSQSCbq7u9Ptubm5FBYW0traSnFxseaURXNqaWnh/PPPd2pOLn5PmtPx59TY2MjYsWOdmpOL35PmdOw5vf3225SVlY30a+YJM9ZaTx1I8FKLChdaa280xnw99Xa/tfbeVFujtfY7xpjbAKy1j6SOWwaMt9auNMasAVZaa19PtW2w1s55H2PWARGg6HjjHqO/hLX2PmPMw8B6a+1/GmPeBv7NWvtgar/rgOustbcZYx4ANhxaGDHGfBD4KfAn1trk0P7/45f/YT/3288d97MUOZNdW3otv2z+ZdBlSJYY+lSa6upqamtrueOOO7jvvvsIh8M8/PDDFBQUcNtttzEwMMDVV1/N2rVrGVy//oN7772XCy+8kOuvvx4YPLNk0qRJp3UuIn5TjsUVyrK44FCOt2/f/mplZeXlJ9OHLqVxx49SP38PfA34r9T2FuDCoxxzPvDp1FkZHwQmH2W/ExkzF7joBMc9mldTP18HpqReR4GHhuxzPnBVquZZQBmAMWYMg2er/OXwRRGA7v7u91mKyJlnV+euoEuQLBeNRnnzzTfp7+/n1VdfTS+CvPLKK1x22WXp7W9961s88cQTAOmzSg4Z+lokUynH4gplWVzgR461MOKOoXec+WvgytTrK4E3Uq+7GbxUhdQlKW8DD6bODLmbwQWOkx2T1DgnMu7RXJH6OYPBM1AADlprB4bs8zbwRKrmZcCbqfd/CDxirT3iMhqAgpyCY05EJBPMLJ4ZdAmS5ZYtW8by5cuZMmUK7e3tLFy4EID169czc+Yf8vmFL3yBJ598kmuvvZb+/n7mzZuXbhv6hBqRTKUciyuUZXGBHznWPUbc1AdcbIzZBLwL3Jd6/3ngJ8aYzwF3Ad8HfmiMWQzEgM96HPffgUdOYNxNRzm+InUmSCPwi6Ps8wxwrTFmI2CBzxtjrmHwPiaTjDG3Ak9ba7819KDuAZ0xIplvZ+fOoEuQLFVbWwvAZZddxiuvvHJE+z333HPY9vjx43n66adH7Ev/OikuUI7FFcqyuMCPHGthxAHW2pVDXj+SevndEfZrAz4x7O0bjtLnnJMYE+DmExx3JA9Yazccq47U2SN/Mey4fUD+sToebRR1yXyRUCToEkQ8SyQSQZcg4plyLK5QlsUFfuRYvy3KcaXO4hgqaq391JnS34k4e9zZh91IUCQT1dfXc+655wZdhogn3d06g08yn3IsrlCWxQV+5FgLI3Jcxzt7JOj+TkQoFDrdQ4r4zo9ntIsETTkWFyjH4gplWVzgR45181XJCsnkEQ+qEck4jY2NQZcg4plyLC5QjsUVyrK4wI8ca2FEssKoUYq6ZL7c3NygSxDxTDkWFyjH4gplWVzgR47126JkBS2MiAsKCwuDLkHEM+VYXKAciyuUZXGBHznWb4uSFfr6+oIuQcSz1tbWoEsQ8Uw5Fhcox+IKZVlc4EeOtTAiWWH0aN1nWDJfcXFx0CWIeKYciwuUY3GFsiwu8CPHWhiRrDAwMBB0CSKe6ZF64gLlWFygHIsrlGVxgR851sKIZAUtjIgLenp6gi5BxDPlWFygHIsrlGVxgR851sKIZIVQKBR0CSKe+fGMdpGgKcfiAuVYXKEsiwv8yLEWRiQrJJPJoEsQ8cyPZ7SLBE05Fhcox+IKZVlc4EeOdUdKyQr74vuY+9DcoMsQ8WReZB7rf74+6DIkA7Xd2RZ0CWl5eXlBlyDimXIsrlCWxQV+5FhnjEhWSFqdMSKZr6G3IegSRDzLz88PugQRz5RjcYWyLC7wI8daGJGskD9Kf+lL5psRnhF0CZLhDhw4wIIFCwDo6OjghhtuYN68eSxfvjy9z9KlS5k/fz73338/ALFYjEWLFnH99ddzyy23kEgkPNXQ3t7u6XiRM4FyLK5QlsUFfuRYCyNyQowxK40xc05gv+nGmOkn2OcGP8Y8kXEP9h88kW5EzmhbO7YGXYJksI6ODmpqajh4cPDvwyeffJJFixaxfv164vE4O3bsoLa2loGBAZ577jn27t3Lnj17eOqpp6ipqWHNmjVMnDiRdevWeapjwoQJfkxHJFDKsbhCWRYX+JFjLYyI36an/pxR444ZNeY0liJyakwtmBp0CZLBRo0axerVqyksLAQgEonw1ltvEY1G2b9/P5MnT+bll1/muuuuA2Du3Lls2bKFL37xi8ydO3iPppaWFkpKSjzV0dnZ6W0iImcA5VhcoSyLC/zIsW6+Ku/Hnxpj/g4IA58C/hGYBOwDFgPfAD4NYIy5xVpbaYwZC/wImAjstNZ+ycOYVwPtwCPHG3d4J/agJbI6Qrw/Tn5OPud9/Dz2XLSHqpIq9nbvpae/hwvGXcCmtk1UFFUQMiE2tm+kckIldQfrAJg6dirrWtcxu3g2SZtkW3QbsyKz2B3fTV5OHlPyp7C2ZS1VJVXE+mLs6tzFzOKZ7OzcSSQUYXLe5HR7W7KNuq46rhh/BTtiO5g0ZhJlY8rS7U29TTT0NjAjPIOtHVuZWjCVSCiSbt/fs5+2ZBuXFF7C5vbNTCucRnh0ON2uObk5p4+N/xj5o/KdmpOL39OZOKeGhgaSySTl5eX09PTQ0tLChRdeyNNPP82//uu/MnnyZOLxOLFYDGstra2t5OTk8Lvf/Y6enh6am5t5/fXXaWtrY+LEibS3t9Pf309XVxfl5eU0NjYSCoUoKiqipaWFoqIiEokE3d3d6fbc3FwKCwtpbm6moKCA7u5uenp60u15eXnk5+fT3t7OhAkT6OzsJJFIpNvz8/PJzc0lGo1SUlJCNBpNz6mxsZGCggJycnKIxWKUlpbS1taGtZbS0lKampoYN24cAPF4nLKyMpqbmzHGEIlEaG5uJhwOn/ScWltbKS4u1pyyaE4tLS1EIhGn5uTi96Q5HX9OHR0dh43pwpxc/J40p2PPqbm5mVGjvJ3zYay1njqQ7GCMWQlcaK290Rjz9dTb/dbae1Ntjdba7xhjbgOw1j6SOm4ZMN5au9IYswZYaa19PdW2wVo7532MWQdEgKLjjTvc937+PXv7f9/u4RMQCV4kFKEteeY8XUQyx9Cn0lRXV1NbW8sdd9zBfffdRzgc5uGHH6agoIDdu3ezcOFCKioqqK2t5Z133uHLX/4y7e3tLFy4kEcffZSzzz7bUy29vb2MGaOz+CSzKcfiCmVZXHAox9u3b3+1srLy8pPpQ5fSyPvxo9TP3wNfA/4rtb0FuPAox5wPfDp1P5EPApM9jJkLXHSC4x4mPDr8PocVOfNUlVQFXYI4JBqN8uabb9Lf38+rr76KMYbp06ezZcsWAHbt2sU555xDIpFg8eLF3HPPPZ4XRQAaGxs99yESNOVYXKEsiwv8yLEupZH3o2vI678GrgReSP18I/V+NzABwBhjgLeBrdbaHxpj/ozBBY6THZPUOMcd1w47FUqP6xUX7O/ZH3QJ4pBly5Zxxx13sG/fPi6//HIWLlzIwMAA1157LY2Njbzwwgs8//zzPPbYY7z22ms88MADPPDAAyxevJjrr7/+pMfVoyHFBcqxuEJZFhf4kWMtjMjJ6gMuNsZsAt4F7ku9/zzwE2PM54C7gO8DPzTGLAZiwGc9jvvvwCMnMO6mw4q1fR6HFQmeLqMRP9TW1gJw2WWX8corr4zY/uKLL3LnnXcSDodZsmQJS5Ys8W383Nxc3/oSCYpyLK5QlsUFfuRY9xiRrLBhwwZ76aWXBl2GiCf19fWce+65QZch4olyLC5QjsUVyrK44FCOvdxjRGeMyBkhdQ+SoaLW2k/51f/o0Yq6ZD6vj0kVORMox+IC5VhcoSyLC/zIsX5blDPCsZ5O44f+/v5T2b3IaRGNRikoKAi6DBFPlGNxgXIsrlCWxQV+5FhPpZGsoEvGxAXJpG4iLJlPORYXKMfiCmVZXOBHjrUwIlkhFAoFXYKIZ+Xl5UGXIOKZciwuUI7FFcqyuMCPHGthRLKCVsPFBX48o10kaMqxuEA5Flcoy+ICP3KshRHJCjk5OUGXIOKZrgEWFyjH4gLlWFyhLIsL/MixFkZERDKEFvjEBcqxuEA5Flcoy+ICP3KshRHJCnoqjbggFosFXYKIZ8qxuEA5Flcoy+ICP3KshRHJCrr5qrigtLQ06BJEPFOOxQXKsbhCWRYX+JFjLYxIVujr6wu6BBHP2tragi5BxDPlWFygHIsrlGVxgR85Hu1DHSJnvPfi7zHnoTlBlyHiyaKyRTzV9FTQZUiGaLvzzPyfXWtt0CWIeKYciyuUZXGBHznWGSOSFTr7O4MuQcSzje0bgy5Bskh7ezsvvvgira2tvvar07bFBcqxuEJZFhfoUhqRE1SYUxh0CSKeVU6oDLoEyUAHDhxgwYIFAKxevZrq6mqqq6uZNWsWy5cvp6OjgxtuuIF58+axfPlyADo6OrjpppvYvn07n/zkJ2lpafGtnqamJt/6EgmKciyuUJbFBX7kWAsjkhV6B3qDLkHEs7qDdUGXIBmmo6ODmpoaDh48CMCSJUuora2ltraWq666iltvvZUnn3ySRYsWsX79euLxODt27OCNN97gm9/8Jl/5yleYN28er732mm81jRs3zre+RIKiHIsrlGVxgR851sJIgIwxK40xc05h/w8O255ujJl+qsbzy6n+XEREssWoUaNYvXo1hYWHnzXX0NDAgQMHmDFjBpFIhLfeeotoNMr+/fuZPHkyH/3oR6moqGDz5s1s376dioqKgGYgIiIicuppYcRh1tplw96anvqTdcaMGhN0CSKeTR07NegSJMOEw2HC4fAR7//gBz9gyZIlAFx55ZW8++67fPe73+W8886juLgYGLyR2dNPP8348eN9feR5PB73rS+RoCjH4gplWVzgR471VBofGWPGAI8Ak4B9wGLgOWAb8BFrbZUxphh4CsgBDLDBGDMW+BEwEdhprf1Sqr8NQ489yph5qTHPAjqAG6y1Bw8db62dk3r9D8CnU69vsdZWGmO+AbxlrX3CGLMS2A1cAGyw1m4wxtyWGmYy8Ia19mfGmLuAOuAXqXmEgVZgkbX2iGfijvSZWGsTw+fm5XMxxuQfr5aDnQeJrI4Q74+Tn5PPeR8/jz0X7aGqpIq93Xvp6e/hgnEXsKltExVFFYRMiI3tG6mcUJm+fGHq2Kmsa13H7OLZJG2SbdFtzIrMYnd8N3k5eUzJn8LalrVUlVQR64uxq3MXM4tnsrNzJ5FQhMl5k9Ptbck26rrquGL8FeyI7WDSmEmUjSlLtzf1NtHQ28CM8Ay2dmxlasFUIqFIun1/z37akm1cUngJm9s3M61wGuHR4XS75uTmnMaMGsN1E69zak4ufk9nypw6OjqIRqOUlJTQ29tLfX095eXlNDQ08OKLL/KlL32J+vp6/vEf/5GvfOUrFBQUsGbNGlatWsUXvvAFAO644w4effRRHnvsMa655hoikQjNzc2Ew2H6+/vp6uqivLycxsZGQqEQRUVFtLS0UFRURCKRoLu7O92em5tLYWEhfX19xGIxuru76enpSbfn5eWRn59Pe3s7EyZMoLOzk0QikW7Pz88nNzc3PadoNEoymUy3FxQUkJOTQywWo7S0lLa2Nqy1lJaW0tTUlD7NNh6PU1ZWRnNzM8YYX+bU2tpKcXGx5pRFc+rr66O3t9epObn4PWlOx59Tbm5u+r8PrszJxe9Jczr2nPr6+jzfZ8ToEU3+McbcARRZa+9NLTQ0Ag8Cn7XWrknt81Wg11r7oDHmeeBeBs/iGG+tXWmMWQOstNa+bozpGXrsUca8Eyiw1v6DMWYxgwsYW1Nt6YWR1PZtANbaR1LbHwL+xVr7SWPMK8A84KscuTCyGfiKtfZ2Y8yvgM8wuIDy/6SO/SSwyVrbcSKfibX2O8Pn5uVzMcZcdrxanvjlE/bm3958tI9RJCPocb3yfgx9XG91dTW1tbUAvPzyy/ziF7/gH/7hHwC45ZZb+NKXvkRFRQV/8Rd/wezZs+no6KCsrIybbrqJr371q8yfP5/KSn9u/vvuu+9y9tln+9KXSFCUY3GFsiwuOJTj7du3v1pZWXn5yfShS2n8dRHwX6nXW4ALgV3DFjb+CDh0F7vfpn6eD3w6dSbEBxk8Q4MRjh3JBcDW1OtHGDyT4oRYa/cAhan7eeyy1nYP2yU/td/vgLOMMWGgw1rbBWwHdhljngOqgINHGWakzwT8/VyOW4tFC4CS+ZI2GXQJ4oD169czc+bM9PayZctYvnw5U6ZMob29nYULF/KFL3yBJ598kmuvvZb+/n7mzZvn2/jGGN/6EgmKciyuUJbFBX7kWJfS+OsN4ErghdTPN4BLh+3ze+Bi4EUGz4hYC7wNbLXW/tAY82epfQBO5GKp3UAFsA74G+AA8P2j7NsNTAAwxhg7eLrQE8Bq4AupfRLAoQdBXw08nXq9FVgGPJPavhR42Vr7N8aY/wA+nqphuJE+k5Hm5uVzOW4tXf1dI30eIhllW/SE1z1FDnPobBGAe+6557C2yy67jFdeeeWIY55++ukj3vNDJBI5Jf2KnE7KsbhCWRYX+JFjnTHir38HLjbGbAI+zOAZHMN9D1iYOgvi0B3xvg9ckzrur4B338eY3wf+ONXfHwM/Psa+zwPXG2NeZnDxAOCngAVeSm0/Ayw1xnyHwft1HPIUgwsjv0ht7wXuNMZsBsr5w1kew53IZwLePpfj1jIuR48ik8w3KzIr6BJEPGtubg66BBHPlGNxhbIsLvAjx7rHSBYzxlwM/BD4rrX2B0HXcyr95je/sdOmTQu6DBFP2tvb008MEclUyrG4QDkWVyjL4oJDOfZyjxFdSpNBUmdTDBW11n7qZPuz1r4BXOGpqCH8rk9EDtff3x90CfB53GQAACAASURBVCKeKcfiAuVYXKEsiwv8yLEWRjLI0CfMnInO5Pr0l764oKuri5KSkqDLEPFEORYXKMfiCmVZXOBHjnWPEckKoVAo6BJEPCsvLw+6BBHPlGNxgXIsrlCWxQV+5FgLI5IVkkk95lQyX2NjY9AliHimHIsLlGNxhbIsLvAjx1oYkaygZ7SLC3Tmk7hAORYXKMfiCmVZXOBHjrUwIlkhJycn6BJEPCsqKgq6BBHPlGNxgXIsrlCWxQV+5FgLI5IV+vr6gi5BxLOWlpagSxDxTDkWFyjH4gplWVzgR461MCJZQWeMiAv0rzriAuVYXKAciyuUZXGBzhgROUHW2qBLEPEskUgEXYKIZ8qxuEA5Flcoy+ICP3KshRHJCgMDA0GXIOJZd3d30CWIeKYciwuUY3GFsiwu8CPHo32oQ+SM97vo75j70NygyxDxJBKK0JZsC7oMOcO03ZlZmSgvLw+6BBHPlGNxhbIsLvAjxzpjRLJCeHQ46BJEPKsqqQq6BBHPGhsbgy5BxDPlWFyhLIsL/MixFkYkK/Tb/qBLEPFMZ4uIC3Jzc4MuQcQz5VhcoSyLC/zIsRZGAmKMWWmMmRN0HSMxxmx4H/sGPg9jzJTj1dA70HuaqhE5deq66oIuQc5gBw4cYMGCBQCsXr2a6upqqqurmTVrFsuXL6evr49LLrkk/f6bb74JwNKlS5k/fz7333//aamzsLDwtIwjciopx+IKZVlc4EeOtTAiLpgCzDnWDmNzxp6WQkROpSvGXxF0CXKG6ujooKamhoMHDwKwZMkSamtrqa2t5aqrruLWW2/ljTfeYOHChen3L7roImpraxkYGOC5555j79697Nmz55TX2traesrHEDnVlGNxhbIsLvAjx7r5qk+MMWOAR4BJwD5gMfAcsA34iLW2yhhTDP8/e3cfXlV153///SUk5CTkhISEpCCCLaVisYWpcVqsgMYBxMaiThX7KLZTHVq8bat1nPbn0F/F3tNpOxanttURGR1bR1udNopSRR6s4KDGB4K3jDBDqmKec3KSkIeTsO4/ckhDDIRwDtnJyud1Xblyzt5r7/1dOZ9is7LW3jwMpAAGbDGzDOA+YBKwyzn3tfj5tvQ5Nj1+/lOACHA53QNbvwEygb3OuRVmthpIBc4FwsCSePu+x9Lfdfvp13vqO0o/VgN/CWQANcBy51xnvB+/A1Y45z5iZgbcBcyMt7sCOAT8CzAHiAHLgap+2n0B+Gj8qzDej+L4z3pCfNbIZ5xzNX370drUSu66XJq7mgmlhJh57kz2nbGPxXmL2d+6n7auNk4ffzrb6rdRlF1EqqWytWErxROL2Xuw+6/0MzJmsKluEwtyFhBzMV5ofIH5ufN5o/kN0lPSmR6azsbajSzOW0y0M0p5Uznzcuaxq2kXuam5TEmf0rO/PlbP3pa9nD3hbF6OvszkcZMpGFfQs7+qvYoD7QeYG57LzshOZmTOIDc1t2f/O23vUB+r58ysM9nesJ3ZWbMJjw337Fef/OzThLETWDZpmVd98vFzGuo+NTc3U1NTw+rVq7npppuoqKggFAqRlpbGm2++ybvvvktBQQEPPPAATz75JJs2bWLWrFmsWbOGJ554ggsvvJC3336bj3zkIzz77LOMHTuW8ePHA9Dc3ExBQQE1NTWYGbm5udTU1BAOh+nq6qKlpYXCwkIqKytJTU0lOzub2tpasrOz6ejooLW1tWd/WloaWVlZtLe3E41GaW1tpa2trWd/eno6oVCIhoYGJk6cSFNTEx0dHT37D/epsbGRvLw8GhsbicViPfszMzNJSUkhGo2Sn59PfX09zjny8/Opqqo6qX2qq6sjJydHfRpFfWpvb6e9vd2rPvn4OalPA/dpzJgxVFRUeNUnHz8n9enYfWpvb6eqqqq/X2ePmznnEjqBdDOzrwPZzrk18UGCSuB24LPOuUfibW4C2p1zt5vZU8AaugcDJjjnVpvZI8Bq59xrZtbW59jrgEzn3A/MbAWwG2ige+DgaeBJugcU/haY5Zy7wsxuAfYCef0cO6+/68avtcU5tzD++vq+7YAL++nHQqDDOXebmf0MeMY591sz2wP83Dl3e/x8y4BlzrmrzOwnwJb4j/Ai59w1ZvYpwNE9uNO3XS7wFeA84ErglPj1FgILnXOrj/b5/Ptj/+6+8NIXju/DFBmmzs89n2fqnwm6DBlmej+VpqSkhNLS0p733//+91m4cCHnnnsuZWVlTJ48mcLCQv72b/+Wiy++mA0bNnDNNdcwe/ZsnnnmGV577TWuv/76k1pvVVUVBQUFJ/UaIiebciy+UJbFB4dzXFZW9lJxcfFZJ3IOLaVJnjOA/4q/fh6YBZQfHtiIOw14Nf76xfj3DwGXxGdWvB+YEt/e99jTgZ3x1+k0So3ug4AG6Bw1C8f33xb//CUg7yrFHu25f/bXrrx8AL8W/v0b38haARmBtn/N9In6++UBB7/qcc48BTxylHcCvnXOxXn07LmNNk6Nk5CsYp//jIsfv0KFDPPvss3zyk58E4MMf/nDP4+zmzJnDvn37yMzMpLW1FYCWlhYOHTp00utqa2s76dcQOdmUY/GFsiw+SEaONTCSPLuBj8dffzz+vrlPmz8BH46/nhP/vge4PT5D47vxNvRz7BtAUfz139M9IPJlupfSXAm09GrbcuSh/R57tOv21V+7/voBcPgGCHPpnqkCcNA51/v/ae8BHoyf73rg9d71mdnngO8fpV1/fQNopXsJD/GlOu8R7YwepXsiI8fG2o1BlyAjyI4dO/jYxz7G4X8Wr732WsrLy+nq6mLDhg3Mnj2bOXPm8PzzzwNQXl7OqaeeetLrOjw4IzKSKcfiC2VZfJCMHGtgJHn+FfiwmW0DPkj3zIy+7gIui8+CCMe33Q1cGD/uWuCto5z/buAv4sf+BXA/8BRwM3B4bv3RZn30d+xgrtu3XX/9ACiKb5sAPHaU8/0emGxmW4FbgQqgFHDxa3yB7iVI/bU7mpeBD5nZs3Tfi+Q9wmPD/W0WGVEW5y0OugQZQZ555hnmzZvX8/7GG2/k2muvZf78+RQVFbFw4UKWLl3KQw89xHe+8x3+8z//k0WLFp30uiorK0/6NURONuVYfKEsiw+SkWPdY0SSIn5flS3OuS0Bl9Iv3WNEfKB7jEh/et9j5EREIhE2b97MvHnzhmSdudaziw+UY/GFsiw+SMY9RnTjBUmKY934dDiYPmF6wr88iAQtGo0SDmv2kyTXhAkTuOSSS4bseqFQaOBGIsOcciy+UJbFB8nIsZbSyKjQ2dkZdAkiCWtoaAi6BJGEKcfiA+VYfKEsiw+SkWMNjMioMHasJkfJyDdx4sSgSxBJmHIsPlCOxRfKsvggGTnWwIiMCkPxCEqRk62pqSnoEkQSphyLD5Rj8YWyLD5IRo41MCKjggZGxAcdHR1BlyCSMOVYfKAciy+UZfFBMnKsgREZFVJTU4MuQSRhyXhGu0jQlGPxgXIsvlCWxQfJyLEGRmRUiMViQZcgkrBkPKNdJGjKsfhAORZfKMvig2TkWAMjMiqMGaOoy8inR+qJD5Rj8YFyLL5QlsUHelyvyHEys6BLEElYWlpa0CWIJEw5Fh8ox+ILZVl8kIwca2BERoWurq6gSxBJWGNjY9AliCRMORYfKMfiC2VZfJCMHGtgREaFsWPHBl2CSMLy8vKCLkEkYcqx+EA5Fl8oy+KDZORYvy3KqPCnxj9x7tpzgy5DJCEX5V/E4zWPB12GDBP119UHXcIJaWxsJDMzM+gyRBKiHIsvlGXxQTJyrBkjMiqMUdTFA+Gx4aBLEI80NDSwefNm6urqhvS6ekqY+EA5Fl8oy+KDZORYvy2OUGa22swWBl3H8TKzLYNom/S+RTujyTydSCA21m4MugQZhqqrq1m6dCkA69ato6SkhJKSEubPn883vvGNI9otWLAAgEgkwvLlyykrK+Piiy+mtrZ2yOotLCwcsmuJnCzKsfhCWRYfJCPHGhiRUUF/aRcfLM5bHHQJMsxEIhFWrlzJwYMHAbj66qspLS2ltLSUT3ziE3zxi1/saXvLLbfQ1tYGwO7du7n11lv51re+xfnnn8+rr746ZDVXVlYO2bVEThblWHyhLIsPkpFj3WNkmDCzccB6YDLwNrAC+APwAvAR59xiM8sBHgZSAAO2mFkGcB8wCdjlnPta/Hxb+hybHj//KUAEuJzugbHfAJnAXufcCjNbDaQC5wJhYAlwbT/bIv2cj/5q6aev76n5KH07Wi1bnHNbzOyq+ClXAdVAB1AI3Ouc+0Xva3a4jqP/8EVGiP2t+4MuQYaZMWPGsG7dOj73uc8dsf3AgQNUV1czd+5cALZt20ZGRgaTJk0C4JxzzgFg+/btlJWVceONNw5ZzVrLLj5QjsUXyrL4IBk51sDI8PE3QLlz7sr4gMDVwMeBtc65w/+P9avAY865283sqV7byp1zq83sETP7iHPutaMc+6pzbrmZrQBmAw3AHcDTwJNmVhBvO8M5N9/MbgHOP8q2vH7ON+8otfT1npqBC/vp29Fq6SsD+AywC7gA+C5wxMDIoZZD5K7LpbmrmVBKiJnnzmTfGftYnLeY/a37aetq4/Txp7OtfhtF2UWkWipbG7ZSPLGYvQf3dheSMYNNdZtYkLOAmIvxQuMLzM+dzxvNb5Ceks700HQ21m5kcd5iop1RypvKmZczj11Nu8hNzWVK+pSe/fWxeva27OXsCWfzcvRlJo+bTMG4gp79Ve1VHGg/wNzwXHZGdjIjcwa5qbk9+99pe4f6WD1nZp3J9obtzM6aTXhsuGe/+uRnn4rCRRSkFXjVJx8/p6HqUzQapaGhgYkTJ9LR0UFFRQWFhYVUVlby85//nMsvv5yKigrC4TBr1qzhxz/+MTfddBMVFRVkZmYyZswY7rvvPrKysqiurqaxsZH8/HyqqqoYP348AM3NzRQUFFBTU4OZkZubS01NDeFwmK6uLlpaWnqumZqaSnZ2NrW1tWRnZ9PR0UFra2vP/rS0NLKysqirqyMtLY3W1lba2tp69qenpxMKhXr61NTUREdHR8/+UChEWloajY2N5OXl0djYSCwW69mfmZlJSkoK0WiU/Px86uvrcc4NWZ9ycnLUp1HUp6amJrKysrzqk4+fk/o0cJ9aWlq865OPn5P6dOw+1dXV0dXVdZRfFY+POecSOoEkh5ndCTzinHvazJbQPVBwjnPurF5tfgH8h3Nus5n9ANgIXEH3gEQDMAG42Tn3hJm92OfYO4HfOuc2mZnFN08D/hnoAj4IfBq4CnjBOfd4rxkZ0/vZdnY/57uzv1ri19/inFsYf/3zvu3i1+7bt4VHqeXwjJG/BVqBq5xzC+OzZK4CVjvnDrcH4MHHH3RXvnjlAJ+CyPB25fuu5Nfv/jroMmSY6P1UmpKSEkpLSwE4dOgQS5YsYePGjZgZP/zhD5k5cybLli07ot1ha9asYdasWVx66aVDUndFRQXTpk0bkmuJnCzKsfhCWRYfHM5xWVnZS8XFxWcNfMR7acbI8LGb7lkeT8e/7wY+2qfNn4APA5uBOXQPHuwBdjrn7jWzT8XbADT3OfYNoAjYBPw93UtPTqV7Kc1DwNZebVv6qa/vtv7Od7Ra+uqvXX996++6HUB+/PUS4NGjXOMIzV19fxwiI8+2+m1BlyAjwI4dO/jYxz7G4THrrVu38uyzz3LPPfewa9currvuOj7wgQ9QUFDA8uXLiUajZGdnD1l9+fn5AzcSGeaUY/GFsiw+SEaONTAyfPwrsN7MtgFvAbcBn+3T5i7gYTP7a7rvvQFwN3BvfDlLtJ9j6NXu3+KzKuqAz9E96+NOuu/bATBlEPX2d76UQdTSt11/fevP74E7zaw4ft3jkpmi9ZMy8hVlF/FO9TtBlyHD3DPPPMO8efN63j/++OM9r0tKSli7di2RSIQVK1Zw//33M2vWLM4//2grFZOvvr6ejIyMIbueyMmgHIsvlGXxQTJyrKU0MipoKY344DMFn+HhqoeDLkOGid5LaUaSt956i6lTpwZdhkhClGPxhbIsPjic40SW0uhxvTIqNHU1BV2CSMK2NmwduJHIMKdp2+ID5Vh8oSyLD7SURuQ4fTD8wRH711WRw3SDNPFBVVWVciwjnnIsvlCWxQfJyLFmjMiokJKSEnQJIgk7/OgzkZFMORYfKMfiC2VZfJCMHGtgRERERERERERGLQ2MyKjQ1dUVdAkiCWtu1mOnZeRTjsUHyrH4QlkWHyQjxxoYkVEhNfVYTwAWGRkKCgqCLkEkYcqx+EA5Fl8oy+KDZORYAyMyKnR2dgZdgkjCampqgi5BJGHKsfhAORZfKMvig2TkWAMjIiIjhJkFXYJIwpRj8YFyLL5QlsUHycixBkZkVBg7Vk+mlpEvNzc36BJEEqYciw+UY/GFsiw+SEaONTAio0IsFgu6BJGEabqr+EA5Fh8ox+ILZVl8oKU0IscpJSUl6BJEEhYOh4MuQSRhyrH4QDkWXyjL4oNk5FjrC2RU+N/G/2X+2vlBlyGSkE9M+AQ7IjuCLkMCVn9dfdAlJESPTxcfKMfiC2VZfJCMHGvGiIwKaZYWdAkiCZsemh50CSIJa2lpCboEkYQpx+ILZVl8kIwca2BERoVoZzToEkQStrF2Y9AlyAjT0NDA5s2bqaurC7qUHoWFhUGXIJIw5Vh8oSyLD5KRYw2MyIhkZrcfZftqM1vYd3t4rNZPysi3OG9x0CXIMFJdXc3SpUsBWLduHSUlJZSUlDB//ny+8Y1vEIlEWL58OWVlZVx88cXU1tYCsGrVKhYtWsSPfvSjQOqurKwM5LoiyaQciy+UZfFBMnKse4zIiOScu34w7Q9x6GSVIjJkNPNJDotEIqxcuZKDBw8CcPXVV3P11VcDcNNNN7F8+XJ2797NrbfeSlFREZFIhFdffZWDBw9y6NAh/vCHP/D1r3+dffv28YEPfGBIa09NTR3S64mcDMqx+EJZFh8kI8eaMSLDmpmFzOwxM9tmZo+a2dj49i292uSY2dNmthlY2N95Wrtah6RekZOpvKk86BJkmBgzZgzr1q0jKyvriO0HDhygurqauXPncs4551BUVMT27dspKyujqKiI5557jmXLlgFw3nnn8fzzzw957dnZ2UN+TZFkU47FF8qy+CAZOdaMERnuzgAOOefmm9nFwHgg0qfNV4HHnHO3m9lT/Z1kXNs4ctfl0tzVTCglxMxzZ7LvjH0szlvM/tb9tHW1cfr409lWv42i7CJSLZWtDVspnljM3oN7AZiRMYNNdZtYkLOAmIvxQuMLzM+dzxvNb5Ceks700HQ21m5kcd5iop1RypvKmZczj11Nu8hNzWVK+pSe/fWxeva27OXsCWfzcvRlJo+bTMG4gp79Ve1VHGg/wNzwXHZGdjIjcwa5qbk9+99pe4f6WD1nZp3J9obtzM6aTXhsuGe/+uRnn75yyld4KfqSV33y8XM62X2qqKggPT2dUChEW1sbzc3NNDU10dHRwbp167jooouorq4mLS2NSCTCQw89RHp6Ou+++y5NTU0456itrSU1NZXXXnuNgwcPUl9fj3OO/Px8qqqqGD9+PADNzc0UFBRQU1ODmZGbm0tNTQ3hcJiuri5aWlooLCyksrKS1NRUsrOzqa2tJTs7m46ODlpbW3v2p6WlkZWVxf/8z/8wffp0WltbaWtr69l/uE8NDQ1MnDixp0+H94dCIdLS0mhsbCQvL4/GxkZisVjP/szMTFJSUohGo+Tn5w9pn+rq6sjJyVGfRlGfamtr+dCHPuRVn3z8nNSngftUWVlJRkaGV33y8XNSn47dp3379lFQUDCY3zHfw5xzCZ1A5GQyMwPWAGcBbwLfcM51mNkW59zCeJtfAP/hnNtsZj8ANjrntvQ+z72l97qry64e2uJFkmz2+NmUN2vWyGjX+3G9JSUllJaWAnDo0CGWLFnCxo0b6f6n88/WrFnDrFmz2LlzJ5dddhlFRUWUlpby5ptv8s1vfnNI649EIkyYMGFIrymSbMqx+EJZFh8cznFZWdlLxcXFZ53IObSURoa7jwLPOecWATnAuf20+RPw4fjrOf2dZKxpcpSMfLmpuUGXIMPYjh07+NjHPtYzKPLTn/6UBx98EIBoNEp2djZz5szpWT5TXl7OqaeeOuR1dnR0DPk1RZJNORZfKMvig2TkWL8tynC3H/hHM/sO0Aa82E+bu4CHzeyvgX7vvJNqurGUjHxT0qcEXYIMY8888wzz5s3ref+lL32JFStWcP/99zNr1izOP/98mpqauOiii6isrOTpp5/mqaf6XX14UrW26p5PMvIpx+ILZVl8kIwcaymNjAp3/e4ud80r1wRdhkhCclNzqY/VD9xQvNZ7Kc2JiEQibN68mXnz5iW8HvdEtLe3M27cuCG/rkgyKcfiC2VZfHA4x4kspdGMERkVZmbPTPiXCZGgVVRUMG3atKDLkBFuwoQJXHLJJYFdv7KyUjmWEU85Fl8oy+KDZORY9xiRUWHMGEVdRr60tLSgSxBJmHIsPlCOxRfKsvggGTnWb4syKmhgRHyQlZUVdAkiCVOOxQfKsfhCWRYfJCPH+m1RRoXOzs6gSxBJWF1dXdAliCRMORYfKMfiC2VZfJCMHGtgREaFsWN1Ox0Z+XJycoIuQSRhyrH4QDkWXyjL4oNk5FgDIzIqHDp0KOgSRBKmR+qJD5Rj8YFyLL5QlsUHycixBkZkVNDAiPigra0t6BJEEqYciw+UY/GFsiw+SEaONTAio0JqamrQJYgkrLCwMOgSRBKmHIsPlGPxhbIsPkhGjjUwIqNCLBYLugSRhFVWVgZdgkjClGPxgXIsvlCWxQfJyLEGRmRU0ON6xQfp6elBlyCSMOVYfKAciy+UZfFBMnKs3xZlVNDAiPggFAoFXYJIwpRj8YFyLL5QlsUHycixnmEqo8LbjW9z7tpzgy5DJCFXvu9Kfv3ur4MuQ5Kk/rr6oEsIRENDA+FwOOgyRBKiHIsvlGXxQTJyrD+jy6hwsOtg0CWIJGxnZGfQJYgkbOLEiUGXIJIw5Vh8oSyLD5KRYw2MyKgwbsy4oEsQSdiMzBlBlyCSsKampqBLEEmYciy+UJbFB8nIsQZGRiAz23ICx8wxszm93q82s4UDtUvkmn2O7/d6QyXFUoK6tEjS5KbmBl2CnATV1dUsXbr0iG033HADTz75JACdnZ2ceeaZlJSUUFJSwuuvvw7AqlWrWLRoET/60Y+GvOZEdHR0BF2CSMKUY/GFsiw+SEaONTAyesyJfyWr3YgS7YwGXYJIwjbWbgy6BEmySCTCypUrOXjwz8v9duzYQXV1NUuWLAFg9+7dXHbZZZSWllJaWsoZZ5xBaWkphw4d4g9/+AP79+9n3759QXVh0AoLC4MuQSRhyrH4QlkWHyQjxxoYGcHMbLyZPWlmz5rZvfFtITN7zMy2mdmjZjbWzH4A/B3wd2a2qdcp/ire7hUzKzxGu77XHWdmvzazrWb2gJmlxbdvMbN/MrON8fc5Zva0mW0GFsa3ZZjZb+LX/Vmvc/Y9NmRmT5jZf5nZr8zs74/S39Xxdlvj5+33hsLhsbqplIx8i/MWB12CJNmYMWNYt24dWVlZAMRiMa6//nqmTp3Khg0bAHjxxRfZuHEjF1xwAatWraKzs5PnnnuOZcuWAXDeeefx/PPPB9aHwaqsrAy6BJGEKcfiC2VZfJCMHJ/QU2niv3xOdM5VJVyBJOJ9wB3A08CTZlYAnAIccs7NN7OLgfHOuZvNbA+Ac259r+NnxNvdApx/jHZ9/Q1Q7py70sxWA1cDvwA+Dqx1zt0Yb/dV4DHn3O1m9lSvbeXOudVm9oiZfcQ591o/x54OvA1cDDznnPusmX2wn/4CPOucuy0+0PJp4Ld9C25vbid3XS7NXc2EUkLMPHcm+87Yx+K8xexv3U9bVxunjz+dbfXbKMouItVS2dqwleKJxew9uLf7h5Uxg011m1iQs4CYi/FC4wvMz53PG81vkJ6SzvTQdDbWbmRx3mKinVHKm8qZlzOPXU27yE3NZUr6lJ799bF69rbs5ewJZ/Ny9GUmj5tMwbiCnv1V7VUcaD/A3PBcdkZ2MiNzBrmpuT3732l7h/pYPWdmncn2hu3MzppNeGy4Z7/65GefThl3CssmLfOqTz5+Tsfbp5aWFhoaGsjOzqajo4OKigqeeeYZpk6dyhVXXMFvfvMbXnvtNc455xzuuusuwuEwa9as4YEHHqC2tpasrCwqKioIhULs3r2biooKCgsLqaysJBQKkZaWRmNjI3l5eTQ2NhKLxXr2Z2ZmkpKSQjQaJT8/n/r6epxz5OfnU1VVxfjx4wFobm6moKCAmpoazIzc3FxqamoIh8N0dXXR0tLSc87U1FSys7Opra3t6VNra2vP/rS0NLKysmhpaSEajdLa2kpbW1vP/vT0dEKhEA0NDUycOJGmpiY6OjpGRJ/q6urIyclRn0ZRn1paWmhvb/eqTz5+TurTwH3q7Ow84r8fPvTJx89JfTp2n1paWqiqSmxowpxzx9fQ7FqgGPgS8ApQANzhnPtuQhXIoJnZFufcQjObDvwz0AV8kO5BgQpgDXAW8CbwDedch5ldBX8e8IgPaLzgnHu8976+7fpeM/76TuAR59zTZrYEuNA59/+Y2YvOubN6HfML4D+cc5vjs1E2AlcA84AGYAJws3PuiX6OnQQ8CbQD/+Kce+Ao/b0K2OGc22hm19A9EPTjvj+ze0vvdVeXXT2In7LI8DN7/GzKm8uDLkOSpPfjektKSigtLeXb3/42ixYt4oILLmDPnj2sWbOGu+++m3Hjum8g/ctf/pJYLMbbb7/NZZddRlFREaWlpbz55pt885vfDKorgxKJRJgwYULQZYgkRDkWXyjL4oPDOS4rK3upuLj4rIGPeK/BLKX5P8A1QAndf7GfSvdMAQnOl4HfLMcGOAAAIABJREFUAFcCLfFtH6V7hsUiIAc4N769FcgAMDOLb2vhvfpr19duumd4EP++O/66uU+7PwEfjr8+fN+SPcDt8UGW78bb9HfsEuD7zrlPOOceiG/rr78AZ8e/zwX29ldwaEzoKF0RGTnOzDoz6BLkJDvttNOoqKgA4JVXXuGUU07h2muvpby8nK6uLjZs2MDs2bOZM2dOz/KZ8vJyTj311CDLHpTGxsagSxBJmHIsvlCWxQfJyPFgl9J0Aovp/uW0HTjaL84yNJ4C7gSujb+fQvcgxT+a2XeANuDFXm0fMrPPATcPcM7e7bb10+ZfgfVmtg14C7jtKOe6C3jYzP4aSI1vuxu418xWAFHgs0c59mXgCTNbBVQDtx6lvwBF8afmVAKP9Xeylq7+xoBERpbtDduDLkFOss9//vOsWrWKRx55hFgsxvr164lEInz1q1/FOceFF17IwoULiUajXHTRRVRWVvL000/z1FNPDXzyYSIvLy/oEkQSphyLL5Rl8UEycjyYpTTfo/vGnG/Q/Rf6TcA259zfJ1yFSB9m9jd0zwyJxb9+5Jzb0k+71cCW/vb19qvHf+U+9+Lnkl+oyBC6KP8iHq95POgyJEl6L6U5EZFIhM2bNzNv3jwKCgoGPmCYOHDgAJMnTw66DJGEKMfiC2VZfHA4x4kspTnuGSPOuX8ws9uBRufcITNb4Zx780QuKjIQ59zddM8uGajd6uM53+TMyQn/EiIStIqKCu6fdn/QZcgwMWHCBC655JKgyxi0WCwWdAkiCVOOxRfKsvggGTke7ON6xwLz4k+l0U0bZMRITU0duJHIMJeMZ7SLBE05Fh8ox+ILZVl8kIwcH/fAiJl9me77PvweSAceNbPrE65AZAhoNFx8kIxntIsETTkWHyjH4gtlWXyQjBwPZsbI/wX+Amh3zjXT/ZSRbyRcgcgQSElJCboEkYRlZmYGXYJIwpRj8YFyLL5QlsUHycjxYAZG2oAO4PDdWjOAroQrEBGR46IBPvGBciw+UI7FF8qy+CAZOR7MwMitdD+6NcvMfgbsAL6fcAUiQ6CrS2N4MvJFo9GgSxBJmHIsPlCOxRfKsvggGTkezFNp7jWz/wLOBwy40zm3O+EKRIaAbr4qPsjPzw+6BJGEKcfiA+VYfKEsiw+SkePjHhgBcM69Drye8FVFhlhnZ2fQJYgkrL6+noyMjKDLEEmIciw+UI7FF8qy+CAZOR7MU2nuNTPdnUdEJCDOuYEbiQxzyrH4QDkWXyjL4oNk5Hgw9xiZBnw04SuKBGDs2EFNjhIZljTdVXygHIsPlGPxhbIsPkhGjgczMPJ9YK2ZfcbMTj38lXAFIkMgFosFXYJIwqqqqoIuQSRhyrH4QDkWXyjL4oNk5Hgwf0ZfF//+w17bHPD+hKsQOckqmio4b+15QZchkpCi7CJeaHwh6DIkQfXX1QddQqDGjx8fdAkiCVOOxRfKsvggGTkezFNpTkv4aiIiIiIiIiIiw8hgbr56an9fJ7M4kWQZN2Zc0CWIJGxGxoygS5Akqq6uZunSpUdsu+GGG3jyySff027BggXHPG4kaW5uDroEkYQpx+ILZVl8kIwcD+YeI1uBLcA2YA/wv/H3chKZ2ZaTeO45ZjYngeNvT2Y9J8rM7jCzTWa23cym99emqatpaIsSOQk21W0KugRJkkgkwsqVKzl48GDPth07dlBdXc2SJUuOaHvLLbfQ1tZ21ONGmoKCgqBLEEmYciy+UJbFB8nI8XEPjDjnTnPOvd85Nx3IAlYB/5ZwBRKkOfGvE+Kcuz6JtZwQM/sLoNo5Vwz8FLiuv3ZZKVlDWpfIybAgZ8HAjWREGDNmDOvWrSMrq/vfplgsxvXXX8/UqVPZsGFDT7tt27aRkZHBpEmT+j1uJKqpqQm6BJGEKcfiC2VZfJCMHJ/QM0ydc53AnWb25ICNJSnMbBywHpgMvA2sALYDS4FddA9w3AP8NXAfMAnY5Zz7mpmFgIeBMFAHfIbupwxdEj/3F5xzxWa2GvhLIAOoAZY75zrjs1Z+B6xwzn2kV01bnHML468N+Jd4HTFgOVAF3AXMjJ/vCudcVz99uwr4UvxtB3C5c64xft1fAjcDi5xzlWb2PaAYaIm3KwPK4sfmA9X9/fxizTFy1+XS3NVMKCXEzHNnsu+MfSzOW8z+1v20dbVx+vjT2Va/jaLsIlItla0NWymeWMzeg3uB7mUMm+o2sSBnATEX44XGF5ifO583mt8gPSWd6aHpbKzdyOK8xUQ7o5Q3lTMvZx67mnaRm5rLlPQpPfvrY/XsbdnL2RPO5uXoy0weN5mCcQU9+6vaqzjQfoC54bnsjOxkRuYMclNze/a/0/YO9bF6zsw6k+0N25mdNZvw2HDPfvXJzz7NGj+LZW6ZV33y8XMaqE8VFRWkpqaSnZ1NW1sbkUiEX/3qV0ydOpVrr72WtWvX8vrrr3P11Vdz6623cs899/CVr3yFiooKCgsLqayspKOjg2g0SkNDAxMnTqSpqYmOjo6e/aFQiLS0NBobG8nLy6OxsZFYLNazPzMzk5SUFKLRKPn5+dTX1+OcIz8/n6qqqp6bmDU3N1NQUEBNTQ1mRm5uLjU1NYTDYbq6umhpaek55+E+1dbWkp2dTUdHB62trT3709LSyMrKIhKJkJ2dTWtrK21tbT3709PTCYVCI7JPdXV15OTkqE+jqE+RSIRJkyZ51ScfPyf1aeA+HTx48Ij/vvjQJx8/J/Xp2H2KRCKkpaX192vgcTPn3PE1NLulz6apQJFz7oRnHMjADg8+mNnXgWzn3Jr4AEYlcD5QClwO/Ab4IFALTHDOrTazR4DVQCrwD865i83sYmCbcy4SH5DAObc+fq3VQIdz7jYz+xnwjHPut2a2B/i5c+6IpTN9BkYuBi5yzl1jZp+i+4lFqcAy59xVZvYTYItz7vf99PEqYJ5z7qtmdiNwyDn34/jAyPPAzc45F1/288/OufPM7Lp47Wvj58ihe7nXQufcex758K+//1f3Ny//zeB++CLDzJRxU3in/Z2gy5AE9X4qTUlJCaWlpXz7299m0aJFXHDBBezZs4c1a9Ywe/ZsZs6cybJly3ra9T1uJDp48CAZGRlBlyGSEOVYfKEsiw8O57isrOyl4uLis07kHIO5x4j1+XoduPBELion5Azgv+Kvnwdm0T1T4nLgcbpngbwEfAi4JD6o8H5gSrxduZn9AVgMHGtx+kvx768B0+OvG4G1A9R3OrATwDn3GPBEvJZPxGuZDxxr8Vd/1wW41f159O5DwPvj5/ssMBF6ZqvcA3y3v0ERgPEpehSZjHzzc+cHXYKcJKeddhoVFRUAvPLKK5xyyils3bqVe+65h5KSEnbt2sV11/W7UnDE0bRt8YFyLL5QlsUHQ7qUxjn3vd7vzWwM3TMCZGjsBj4OPB3/vhuoAP4P8A3gDuBrwDRgp3Pu3vjMjT8BHwWec879vZn9CjgX2AS0cuTgAsDZwEZgLt2DGwAHnXOHBqjvDbqX9dxjZp+jeyDnBeBB59w/mNkn6Z5FcjRn071sZi6w9/BG51zvWwzvoXvWyZfMbHa8rwC30b1s6D2zUQ5rO9Q2QPkiw98bzW8EXYKcJJ///OdZtWoVjzzyCLFYjPXr1zN58uSe/SUlJaxdO9D49MgQDoeDLkEkYcqx+EJZFh8kI8fHPTBiZr90zl3T+/p039tiasJVyPH4V2C9mW0D3qJ7MCCb7sGR/6H7BqQVZnY3cK+ZrQCidM+sGAP8o5l9B2gDXoyf8yngofhAxs3xbUXxGRmVwGODqK8UuDBe30HgC3Tfz+QiM9tK96DI549x/FQz2xyv7/L+GjjnXjGzt+LnSwOuMbNZwLeBP8br3uGcu7nvsWNsMJOjRIan9JT0oEuQJDu8HCYrK4v169cP2O5o70eSrq733GpKZMRRjsUXyrL4IBk5HszNV0uA3gMj0UEeLyfg8D08nHPtwJV9dtfQPTMDupfM4Jxrof+BhcX9nLseuODwezM7H/iJc25LfzUcrbb4awf8bT/NjvfGHr86fK+TY13XOffdfo5NGejkaZbYzXhEhoPpoensiOwIugyRhLS0tJCXlxd0GSIJUY7FF8qy+CAZOR5wYMPMvgRcBeSa2TO9dp0CPJrQ1WVYcc6tPtnXMLMHgcI+my90zrWezOtOnTD1iBseioxE7e3t/Gzcz4IuQyQhhYV9/xMgMvIox+ILZVl8kIwcH8+Mjy10L9f4LdD7PiO1zrndCVcgo4pzbnkQ143FYkFcViSpKisrmTZt2sANRYYx5Vh8oByLL5Rl8UEycjzgwIhzrgKoMLPdzrmtCV1NJCB/vresyMiVmqr7XcvIpxyLD5Rj8YWyLD5IRo6P+46Uzrn3PCfSzLISrkBkCKSkDHgbEpFhLzs7O+gSRBKmHIsPlGPxhbIsPkhGjo97YMTMLjCz/zKz/zn8BRxIuAKRIdDZ2Rl0CSIJq62tDboEkYQpx+ID5Vh8oSyLD5KR48E8VeZOuh/BegfwdWDZII8XCYxmjIgP9Fcd8YFyLD5QjsUXyrL4YEhnjACZwAvAU3Q/keYfeO/jY0WGpe6nCYuMbB0dHUGXIJIw5Vh8oByLL5Rl8UEycjyYGR+PAw8C/wz8DDgL0P+SZEQ4dOhQ0CWIJKy19aQ+1VpkSCjH4gPlWHyhLIsPkpHjwQyMXAMUOed2mtmPgY8DlydcgcgQ0B23xQfJeEa7SNCUY/GBciy+UJbFB8nI8WCeSuOAl8xsKt0zR/7BOfdSwhWIDIFYLBZ0CSIJq6ysDLoEkYQpx+ID5Vh8oSyLD5KR48E8leZTwFvAa8B44L/N7IqEKxAZAmPGDOZ2OiLDU1paWtAliCRMORYfKMfiC2VZfJCMHA9mKc0dwEJgq3Ou0cw+AjwL/EfCVYicZHsje1mwdkHQZYgk5AOhD7CvdV/QZUhc/XX1QZcwImVlZQVdgkjClGPxhbIsPkhGjgfzZ/QxdM8YOfx4jyb0uF4ZITJSMoIuQSRhZ084O+gSJIkaGhrYvHkzdXV1QZcypEZbf8VPyrH4QlkWHyQjx4MZGPkFUApkmNmNwDPAXQlXICOGmW05gWPmmNmck1DOoLQe0h23ZeR7Ofpy0CVIP6qrq1m6dCkAnZ2dnHnmmZSUlFBSUsLrr7/e0+6GG27gySefBCASibB8+XLKysq4+OKLqa2tDaT2IOTk5ARdgkjClGPxhbIsPkhGjo8548PMPuOcexjAOfcDM3sZuAAoBG5xzj2RcAXiu8ODIq8EWUSq6ak0MvJNHjeZN1reCLoM6SUSibBy5UoOHjwIwO7du7nssstYvXr1Ee127NhBdXU1S5Ys6Wl36623UlRURCQS4dVXX6W4uHioyw9Ea2sr4XA46DJEEqIciy+UZfFBMnI80IyRn/Z5P8U5d4Nz7lsaFBm9zGy8mT1pZs+a2b3xbSEze8zMtpnZo2Y21sx+APwd8HdmtinebrWZPWFmW83sN/F2nzOz6+P7rzSzG63bA2b2vJn91sx+YmYpZvYrM3vOzH5nZqlmdpWZbY5/bTSz7P5qHmta9SUjX8G4gqBLkD7GjBnDunXreta2vvjii2zcuJELLriAVatW0dnZSSwW4/rrr2fq1Kls2LABgHPOOYeioiK2b99OWVkZRUVFQXZjSLW1tQVdgkjClGPxhbIsPkhGjgf6bdH6vP8+cE/CV5WR7n1034z3aeBJMysATgEOOefmm9nFwHjn3M1mtgfAObe+1/HPOuduM7OfAZ+me4nWvwO3A4uB7wE5wCTn3MfNrMw5d5mZTQIep/uGv/cCfxE/35vOua/Gl3h9Bfhx34JbmlrIXZdLc1czoZQQM8+dyb4z9rE4bzH7W/fT1tXG6eNPZ1v9Noqyi0i1VLY2bKV4YjF7D+4FYEbGDDbVbWJBzgJiLsYLjS8wP3c+bzS/QXpKOtND09lYu5HFeYuJdkYpbypnXs48djXtIjc1lynpU3r218fq2duyl7MnnM3L0ZeZPG4yBeMKevZXtVdxoP0Ac8Nz2RnZyYzMGeSm5vbsf6ftHepj9ZyZdSbbG7YzO2s24bHhnv3qk599SrVUlk1a5lWfRvLn1NbWRkNDA+PHjycWi1FRUcGHP/xhfvaznzFp0iS+973v8cADD9DW1sb06dO59NJLKS0t5bXXXuOLX/wi4XCY++67j8zMTCKRCA0NDRQWFlJZWUlaWhpZWVnU1dWRk5NDa2srbW1tPfvT09MJhUI0NDQwceJEmpqa6Ojo6NkfCoVIS0ujsbGRvLw8GhsbicViPfszMzNJSUkhGo2Sn59PfX09zjny8/Opqqpi/PjxADQ3N1NQUEBNTQ1mRm5uLjU1NYTDYbq6umhpaek5Z2pqKtnZ2dTW1pKdnU1HRwetra3v6VNXVxfRaNSrPvn4OalPx+5TV1cX7e3tXvXJx89JfRq4T2lpaVRUVHjVJx8/J/Xp2H3q6uqiqqpqgF9hj82cc0ffaXbAOTf5aO9ldDGzLc65hWY2HfhnoAv4IN2DGxXAGuAs4E3gG865DjO7Cv48MGJmq4EdzrmNZnYN3QMoPzazh4EVwIPOuU+ZWTrwB2Ac8FC8TQ5wJ5AOTAK+A0wHxjnnfmlmi4FPOedW9a39wccfdFe+eOVJ+KmIDJ0r33clv37310GXIXG9n0pTUlJCaWkp7e3tjBs3DoBf/vKXxGIx/vSnP7Fo0SIuuOAC9uzZw5o1a7jvvvt6jl2zZg2zZs3i0ksvHfI+BKGiooJp06YFXYZIQpRj8YWyLD44nOOysrKXiouLzzqRcwy0lCbLzG47/NX3fXybjD5fBn4DXAm0xLd9FHjOObeI7tke58a3twIZAGZ2eAbS4UdrzAX2xl8/BnwTeK5Xm0edc3/pnDs8A+RSoDz+/Z1e9fR3viN0us7B9VBkGKpqT2wkXE6+a6+9lvLycrq6utiwYQOzZ8/mtNNOo6KiAoBXXnmFU045hZ/+9Kc8+OCDAESjUbKz+10F6KX09PSgSxBJmHIsvlCWxQfJyPFAS2l+NMB7GZ2eonvmxrXx91OA3cA/mtl3gDbgxV5tHzKzzwE3x7cVxZ9wU0n3gAjA74D9wOGF9m8AD8SX5dTTvczmOeAhYCndAy5T4m2nmtnm+HUv76/gmIudeG9FhokD7QeCLkEGcOONN/LVr34V5xwXXnghCxcu5GMf+xirVq3ikUceIRaLsX79ejIyMlixYgX3338/s2bN4vzzzw+69CETCoWCLkEkYcqx+EJZFh8kI8fHHBhxzn0v4SuIN5xzC+PftwGz+2myuJ9j6ul+khEAZnY+8BPn3JY+7SLAhF6bioD/ATqBVLpv/Pss8JHex8WX6vyqzz1M3iM0Rv/oy8g3NzxXT6UZpkpLSwE444wz+OMf/3jEvqysLNavX/+eYx599NGhKG3YaWho0BMQZMRTjsUXyrL4IBk51qM6ZEg551YfZ7vH6b7R6kDt1h/P+Q52HTyeZiLD2s7IzqBLEEnYxIkTgy5BJGHKsfhCWRYfJCPHGhiRUWHGhBlH3ChRZCR69913ed/73hd0GSIJaWpq6rlbvchIpRyLL5Rl8UEycjzQzVdFvHDo0KGgSxBJWEdHR9AliCRMORYfKMfiC2VZfJCMHGtgREaF1NTUoEsQSVhhYWHQJYgkTDkWHyjH4gtlWXyQjBxrYERGhVhMT6WRka+ysjLoEkQSphyLD5Rj8YWyLD5IRo41MCKjwpgxirqMfHqknvhAORYfKMfiC2VZfJCMHOu3RRkVzCzoEkQSlpaWFnQJIglTjsUHyrH4QlkWHyQjxxoYkVGhq6sr6BJEEtbY2Bh0CSIJU47FB8qx+EJZFh8kI8caGJFRYexYPZlaRr68vLygSxBJmHIsPlCOxRfKsvggGTnWwIiMCpoxIj7QX3XEB8qx+EA5Fl8oy+IDzRgROU7OuaBLEEmYnq4kPlCOxQfKsfhCWRYfJCPHWl8go8J/N/435609L+gyRBKSm5pLfaw+6DK8UX+dfpZBKCwsDLoEkYQpx+ILZVl8kIwca8aIjArhseGgSxBJ2OK8xUGXIJKwysrKoEsQSZhyLL5QlsUHycixBkZkVOhwHUGXIJKw/a37gy5BJGGZmZlBlyCSMOVYfKEsiw+SkWMNjMiocMgdCroEkYS1dbUFXYKXqqurWbp06Xu2LViw4IhtN9xwA08++SQAFRUVXHHFFSxdupTvfve7Q1arD1JSUoIuQSRhyrH4QlkWHyQjxxoYGUXMbLWZLTyOdnPMbM5xnnNLonUNhfQx6UGXIJKw08efHnQJ3olEIqxcuZKDBw8esf2WW26hre3PA1E7duygurqaJUuWALB69WpuuOEGNmzYwIEDB/jjH/84pHWPZNFoNOgSRBKmHIsvlGXxQTJyrIER6c+c+Jc3mruagy5BJGHb6rcFXYJ3xowZw7p168jKyurZtm3bNjIyMpg0aRLQfafz66+/nqlTp7JhwwYA9u3bx0c/+lEA8vPz9X8sByE/Pz/oEkQSphyLL5Rl8UEycqyn0ow+f2Vm/xcIA58G/l9gMvA2sAL4HnAJgJl9wTlXbGYZwH3AJGCXc+5rx3sxM1sNbHHObTGzq+KbpwC7nXP/aWY3A3udcw8f5di/BDKAGmC5c64zPkvld8AK59xHzMyAu4CZ8XZXOOe6ep9rXOs4ctfl0tzVTCglxMxzZ7LvjH0szlvM/tb9tHW1cfr409lWv42i7CJSLZWtDVspnljM3oN7AZiRMYNNdZtYkLOAmIvxQuMLzM+dzxvNb5Ceks700HQ21m5kcd5iop1RypvKmZczj11Nu8hNzWVK+pSe/fWxeva27OXsCWfzcvRlJo+bTMG4gp79Ve1VHGg/wNzwXHZGdjIjcwa5qbk9+99pe4f6WD1nZp3J9obtzM6aTXhsuGe/+uRnn758ypd5rek1r/oU5OfU3t5OQ0MDoVCIzs5OKioqCIfDrFmzhh//+MfcdNNNVFRUsGHDBk477TQuvfRSfv/731NeXs6CBQu47bbbeP/7388f/vAHvva1r1FRUUFBQQE1NTWYGbm5udTU1BAOh+nq6qKlpYXCwkIqKytJTU0lOzub2tpasrOz6ejooLW1tWd/WloaWVlZ1NXVkZOTQ2trK21tbT3709PTCYVCNDQ0MHHiRJqamujo6OjZHwqFSEtLo7Gxkby8PBobG4nFYj37MzMzSUlJIRqNkp+fT319Pc458vPzqaqqYvz48QA0NzcnvU//+7//y7Rp07zqk4+fk/p07D7V1dUxc+ZMr/rk4+ekPg3cp+rqatLT073qk4+fk/p07D7t27ev5w9aJ8qccwmdQEaO+EDDLOfcFWZ2S3xzl3NuTXxfpXPuF4cHMJxz6+PHXQ9McM6tNrNHgNXOudfi+7Y45xYOcM2+AyPbgW85564xsyeAv3bOtRzl2A7n3G1m9jPgGefcb81sD/Bz59zt8XbLgGXOuavM7Cfx6/2+97kefPxBd+WLVw7uByYyzHym4DM8XPWeMUQ5Qb0f11tSUkJpaSk//OEPmTlzJsuWLevZ9u1vf5tFixZxwQUXsGfPHtasWcN9993H888/zx133MHcuXO54YYbAuzJyPLWW28xderUoMsQSYhyLL5QlsUHh3NcVlb2UnFx8Vkncg7NGBl97ot//xNwJ3Bx/P3zwIVHOeZDwLz4/Ukm0D3j47UTuHYIaHXO/beZnWJmYSDS36BILy/Fv78GTI+/bgTW9qnvE/GZJOOB/6/vSZq6mk6gXJHhZWvD1qBL8N7WrVt59tlnueeee9i1axfXXXcds2bNoqKiAoBXXnmFU045BYDZs2fz9ttvc/fddwdZ8oijadviA+VYfKEsiw+0lEZORO9BiBuBjwNPx7/vjm9vBSYCxJep7AF2OufuNbNP0T2ocrw6gMNJXQI8Gn+9E7ge+H1/B/VyNrARmAs8Ed920LkjHjOzB3jQOfcPZvZJ4D3ToLJSsvpuEhlxiicW8+t3fx10GV57/PHHe16XlJSwdu1ampqaWLVqFY888gixWIz169cDcMcdd7By5UoyMjICqnZkqqqqYtq0aUGXIZIQ5Vh8oSyLD5KRYw2MjG6dwIfNbBvwFnBbfPtTwENm9jngZuBu4F4zWwFEgc8O4hq/B+40s2Kgrtf2h4E/AgMluCg+E6QSeOwY17jIzLbSPSjy+b4N2g+1D6JkkeHp8P05JPlKS0uPui0rK6tnMKS3m2+++WSX5aXD645FRjLlWHyhLIsPkpFjDYyMIs651b1er4+//GU/7eqBC/psvvwo51w4wDXLgfn9bH8dyD3WsXE/cc5tOdY147NH/uZYJ3n/hPcfcT8BkZGorq6OiRMnBl2GiIiIiIhXNDAiSROf2dFbo3Pu0yf72OPR1dU1cCORYa65uVkDIzLiKcfiA+VYfKEsiw+SkWMNjEjSDDR75GQdezxSU1NP5ulFhkRBQUHQJYgkTDkWHyjH4gtlWXyQjByPSUIdIsNeZ2dn0CWIJKympiboEkQSphyLD5Rj8YWyLD5IRo41MCIiMkJ0PyRKZGRTjsUHyrH4QlkWHyQjxxoYkVFh7FitGpORLzf3eO5XLDK8KcfiA+VYfKEsiw+SkWMNjMioEIvFgi5BJGGa7io+UI7FB8qx+EJZFh9oKY3IcUpJSQm6BJGEhcPhoEsQSZhyLD5QjsUXyrL4IBk51sCIiMgIocdOiw+UY/GBciy+UJbFB8nIsQZGZFTQP/rig5aWlqBLEEmYciw+UI7FF8qy+CAZOdbAiIwKqampQZcgkrDCwsKgSxBJmHIsPlCOxRfKsvggGTnWozpkVHgr8hafXPvJoMsQSciV77uSX7/766DLOOnqr6sPugQ5iSorK5k2bVrQZYgkRDkWXyjL4oNk5FgzRmRUOMShoEsQSVi0Mxp0CYFqaGhg8+bN1NXVJaWdBEMz+MQHyrH4Qlmn3JC6AAAgAElEQVQWHyQjxxoYkVGhtas16BJEElbeVB50CUOqurqapUuXAhCJRFi+fDllZWVcfPHF1NbWEo1G+cxnPsOll17KF77wBTo6OvptJ8NLdnZ20CWIJEw5Fl8oy+KDZORYS2lkVMhMyQy6BJGEzcuZR8W7FUGXMSQikQgrV67k4MGDAOzevZtbb72VoqIiIpEIr776Kvv372flypWcd955fOtb32LTpk2Ew+H3tCsuLg64N9JbbW0tmZn6N1lGNuVYfKEsiw+SkWPNGAmQma02s4XH2L+lz/s5ZjYnyTXcnszznSgzu8PMNpnZdjObfox2E8xsWZ9tKWb2xLGOaz2kGSMy8u1q2hV0CUNmzJgxrFu3jqysLADOOeccioqK2L59O2VlZRQVFfHlL3+Z8847D+j+D2JeXl6/7WR40V8nxQfKsfhCWRYfJCPHGhgZWebEv5LGOXd9Ms93IszsL4Bq51wx8FPgumM0nwAs67PtXuDUY11jrGlylIx8uam5QZcwZMLhMOFw+IhtzjkeffRRJkyYcMRa0p07d9LY2NgzCHK0djI8dHR0BF2CSMKUY/GFsiw+SEaO9dviEDOzHOBhIAUwYKeZ/QaYBOxyzn3tKMf9ALgk/voLzrliMxsP/AbIBPY651aY2WrgL4EMoAZY7pzrjM8++R2wwjn3kV7n3eKcWxh/bcC/0D34EgOWA1XAXcDM+PmucM519VPfVcCX4m87gMudc43x6/4SuBlY5JyrNLPvAcVAS7xdGVAWPzYfqD7Kz+AK4BvA9Ph5VznndgHfAb7f3zE9xx40ctfl0tzVTCglxMxzZ7LvjH0szlvM/tb9tHW1cfr409lWv42i7CJSLZWtDVspnljM3oN7AZiRMYNNdZtYkLOAmIvxQuMLzM+dzxvNb5Ceks700HQ21m5kcd5iop1RypvKmZczj11Nu8hNzWVK+pSe/fWxeva27OXsCWfzcvRlJo+bTMG4gp79Ve1VHGg/wNzwXHZGdjIjcwa5qbk9+99pe4f6WD1nZp3J9obtzM6aTXhsuGe/+uRnn/5q4l+Rm5rrVZ/6+5xqa2tpaWmhsLCQtrY2Dhw4QHZ2NrW1tXznO9/hn/7pn7j//vv50pe+xJ49e/jWt77F3XffTUVFBTk5ObS2tvL1r3+df/u3f+P+++/n05/+NKFQiIaGBiZOnEhTUxMdHR0UFhZSWVlJKBQiLS2NxsZG8vLyaGxsJBaL9ezPzMwkJSWFaDRKfn4+9fX1/z979x4eZX3n///5IUzI5DAhk8RE8EBdREpB5VthW38roPgzFTcu1vXUw1Xs9lstFdZura27rpu9ttqvrnUt1t2vtlK32/7U2tXWqC0qCqxSFgSqYIstdIkKJuQ4OZBJJpPP748M0xiScLjvcGc+83pcF1dm7sPnfn8yL/GaN/cBay3l5eU0NDRQWFgIQGdnJxUVFTQ2NmKMIRqN0tjYSCQSIZlMpudUX19PKBRKz6m4uJje3l66u7vT63NzcykqKqK5uTk9p3g8nl6fl5eXsXM6VL9Lc3Lxc9KcRp/ToWO5NCcXPyfN6chzam5u/kDNLszJxc9JczrynKy1o30dPCLjdQA5NsaYrwM91tr7jTEvAs8Bk621NcaYp4Aaa+2bqW3TTYvU+2UA1tpHU+/PZKBh8RLwSwYaGV8Ceq21dxljHgRettb+pzHmbeDfrLUfuHRmSGPkcuAya+0Nxpg/BywQApZaa5cZY+4D1llrnxlmXsuA8621XzTGfA3ot9Z+O9XA2ATcZq21qUuB/sVae6ExZmVqPqtSY5QA64FF1tphn9eZulymxlq7bMjyR1PL9w6338M/f9je8OsbhlslkjGioSgtCfcfZTv4cb3V1dXU1tbyne98h4qKCq699lq+/vWvc8kll3DBBRdw9dVX89d//dfpS2qG2073GBlfenp6mDRpUtBliHiiHIsrlGVxwaEcb9u2bevixYvPO54xdCnNifch4I3U69eBG4ArUg2EM4CpxzBWAvgC8GMgCoRTy7emfr4JTEu9jgGrjjDeTGAzgLX2WeAXwFnAx1P1LQAqRtl/uOMCfNP+sQN3FnBGarxPAaWQPlvlEeD2kZoiXkQmRo68kcg4V1VWFXQJgfnc5z7HE088wWWXXUYymeSiiy7iRz/6EW+88Qb33Xcf1dXVPPXUU8NuJ+NLfX190CWIeKYciyuUZXGBHznWpTQn3jvAR4BXGLhk5SEgZq39QeosjXdG2bebDzYS/oqBS2l+wsCZFofMB9YAcxlobgActNb2H6G2XcAS4BFjzKeBWcAW4HFr7T8YY/6MgbNIRjI/NZ+5wO5DC621nYO2eZuBs04+Z4yZDZyeWn4XA5cSHXY2yhDdDFwmhDHGDGq4jCp5+NU/IhknG84WGaq2thaAyZMn8/TTT39g3ec//3k+//nPH7bP0O1kfMnNzQ26BBHPlGNxhbIsLvAjxzpj5MR7GLgydcZEBPg9cKkxZgNwI/DuKPu+CHzSGPMacEHq/W3Ay6n1h842mZcafzLw7DHUVgvYVC2fBe4HngGmGGPWA98ERntW6KnGmFeAhcDq4Taw1v4aeDc13vdSrz8M3AosMsasS91PZVjW2gagK7X/Ud84tqe/52g3FRm3dnftPvJGIuPcoScNiWQy5VhcoSyLC/zIse4x4pjUzVfXWWvXneDjLoM/3v9kvFm3bp0955xzgi5DxJO6ujpOP/30I28oMo4px+IC5VhcoSyLCw7l2Ms9RnQpjWOstTVjfQxjzONA5ZDFl1pru308xv0c/mji6621/3M8402cqKhL5ispKQm6BBHPlGNxgXIsrlCWxQV+5FjfFuWYWWuvPQHHOOrLZI5Gf/+Rbq8iMv51d3cTiehGwpLZlGNxgXIsrlCWxQV+5Fj3GJGsoMaIuCAejwddgohnyrG4QDkWVyjL4gI/cqzGiGSFUCgUdAkinlVWDr2CTSTzKMfiAuVYXKEsiwv8yLEaI5IVEolE0CWIeObHM9pFgqYciwuUY3GFsiwu8CPHaoxIVpgwQVGXzJeXlxd0CSKeKcfiAuVYXKEsiwv8yLG+LUpWUGNEXBAOh4MuQcQz5VhcoByLK5RlcYEfOda3RckKfX19QZcg4llra2vQJYh4phyLC5RjcYWyLC7wI8dqjEhWmDhRT6aWzFdaWhp0CSKeKcfiAuVYXKEsiwv8yLEaI5IV9LhecUFHR0fQJYh4phyLC5RjcYWyLC7wI8f6Z3TJCvs79rNw1cKgyxDx5LqTr+Ox9x8LuoxRtaxsCboEGed6e3uDLkHEM+VYXKEsiwv8yLHOGJGs0N7XHnQJIp6taVoTdAkinlVWVgZdgohnyrG4QlkWF/iRYzVGJCtEJkaCLkHEs6qyqqBL8FVrayuvvPIKzc3NQZciJ1B9fX3QJYh4phyLK5RlcYEfOVZjRI6KMWbdce53rjHmXJ/LOWYJmwi6BBHP9sX3BV3CUTtw4ABLliwBoL29nauuuopPfvKTfPazn6W3t5e2tjauvfZatm3bxuWXX05TUxMAK1as4JJLLuHee+8NsnwZQ3o0pLhAORZXKMviAj9yrHuMyFg71BT5dZBF9Fk9rlcyX0siM+7f0dbWxvLlyzl48CAATz75JMuXL+fCCy/kq1/9KmvXriUSifDNb36TefPm0dbWxhtvvMHBgwfp7+/nhRde4KabbmLPnj38yZ/8ScCzEb/l5uYGXYKIZ8qxuEJZFhf4kWM1RjKcMSYPeBQ4BWgDPgX8BCgAdltrrzfG1AAh4AIgAnwite3g/a5ODflD4CRgh7X2y6Mcdx2wBTjbWltljCkEfjrkuN8Crkht/1lr7WJjTP7RHCNV858C+UAjcK21ti913J8D11trzzbGGOBhYEZqu2ustcmh44W6Q0RXR+lMdhLOCTPjghnsmbWHqrIq9nbvJZ6MM7NwJhtaNjCveB4hE2J963oWly5m98HdAEzPn87a5rUsLFlIwibYEtvCgugCdnXuIi8nj2nhaaxpWkNVWRXtfe3s7NjJ+SXns6NjB9FQlKl5U9PrWxIt7O7azfzJ89nevp0pk6ZQMakivb6hp4H9PfuZG5nL5rbNTC+YTjQUTa/fF99HS6KFOUVz2Ni6kdlFs4lMjKTXa05uzumaymuY3j59XM+pqamJgwcPUlNTw6233sp7773HJZdcQnl5OXV1dezfv59QKMQpp5xCRUUFP/vZz/jVr37FTTfdxD/+4z9y8cUX09TUxJw5c3j11VeZOHEioVCI4uJimpqaKC4upre3l+7ubiorK6mvryc3N5eioiKam5spKSmhu7ubeDyeXp+Xl0c4HKa1tZXS0lI6Ojro7e1Nrw+Hw+Tm5hKLxSgrKyMWi5FIJNLrCwoKyMnJob29nfLyclpaWrDWUl5eTkNDA4WFhQB0dnZSUVFBY2Mjxhii0SiNjY1EIhGSySRdXV3pMbN5Tu+88w4TJkxwak4ufk6a0+hzampqIhwOOzUnFz8nzenIc6qvrycWizk1Jxc/J81p9Dm988479PT0jPTV9agYa62nASRYxpiVQIG19lvGmOuB3wBlwEvAL4FrgS8BH7bWXmOMuQPYndpm8H5vAecDk621NcaYp4Aaa+2bqeOss9YuGnTcOPApa+1TqfdnMtCcSB/XWttgjFkGYK19NLXdzSMdY8i8aoBea+1dxpgHgZettf9pjHkb+Ddr7f2p7ZYCS621y4wx9wHrrLXPDB3vkWcesV/Y/oXj/C2LjA+n551OXbwu6DJGNfipNNXV1dTW1qbfb968mbvuuouf/exnAFhrufXWW9m/fz/f//73ufXWW7nhhhuYPXs2L7/8Mm+++SY333zzCZ+DjK2uri4KCgqCLkPEE+VYXKEsiwsO5Xjbtm1bFy9efN7xjKF7jGS+mcDm1OtHgQPAF4AfA1Hg0AVXP0z9fAfIHWa/LcBZwBWpszLOAKaOctydh5oiKYkRjjvUsRxja+rnm8C01OsYsGrIeB9PjbcAqBhuoHCOrp+UzDe7aHbQJRy31tZWvvGNb/DAAw+klxlj+Od//mdmzZrFL37xCwoKCuju7gYG/gfX398fVLkyhmKxWNAliHimHIsrlGVxgR85VmMk8+0C5qVe/y2wkYFLWq4DugZt13WE/b4AvA3cnzoz5HYGmigj6Rzy/q9GOG43A5fDkLrs5ViOMT/1cy4DZ7kAHLTWDv629DbweGq8mxk4Y+YwExR1cUCmPl2pt7eX66+/nr//+7/n1FNPBeA73/kOjz/+ODBwc9bi4mLOPfdcNm3aBMDOnTs57bTTAqtZxk4ioZthS+ZTjsUVyrK4wI8c6x4jme97wL+nzphoBq4B/hW4MbV+pDMyhu73aSAH+EHq0pp2Bu5XcrReHOa4e1PLf2KM+TRwW+q4R3uMean66oFnR9jmGeAyY8x6wAKfGW6j9r72Y5iKyPi0pmlN0CUclx/96Ee88cYb3Hfffdx3331cf/31fO5zn+P666/nP/7jP/jwhz/MRRddREdHB5dddhn19fW89NJLvPjii0GXLmOgsrIy6BJEPFOOxRXKsrjAjxzrHiMyLqXuMbLOWrvOj/Eef+5xe93r1/kxlEhgrjv5Oh57/7GgyxjV4HuMHI+2tjZeeeUVzj//fCoqhr0yTjJcXV0dp59+etBliHiiHIsrlGVxwaEce7nHiM4YkcClzgoZLGat/Qs/jzE1MtXzFzaRoDU1NfFg2YNBlzGmJk+ezBVXXBF0GTKGdJM/cYFyLK5QlsUFfuRYjREJ3OCn3YjIyHJycoIuQcQz5VhcoByLK5RlcYEfOdYdKSUrJJPJoEsQ8ay9XffKkcynHIsLlGNxhbIsLvAjx2qMSFYIhUJBlyDiWXl5edAliHimHIsLlGNxhbIsLvAjx2qMSFbo6+sLugQRz1padJ8cyXzKsbhAORZXKMviAj9yrMaIiEiG0FPExAXKsbhAORZXKMviAj9yrMaIZIWJE3WfYcl8Ot1VXKAciwuUY3GFsiwu0KU0IkcpkUgEXYKIZw0NDUGXIOKZciwuUI7FFcqyuMCPHKsxIllBjyITFxQWFgZdgohnyrG4QDkWVyjL4gI/cqzGiIiIiIiIiIhkLTVGJCskk8mgSxDxrLOzM+gSRDxTjsUFyrG4QlkWF/iRY92RUrLC79t/z4WrLgy6DBFPTso9iQO9B07Y8VpW6hF+4r+KioqgSxDxTDkWVyjL4gI/cqwzRiQrFOUUBV2CiGcLSxYGXYKIZ42NjUGXIOKZciyuUJbFBX7kWI0RyQoWPaNdMl/CBvN0pQMHDrBkyZIR3/f19TFnzhyqq6uprq7mN7/5DXV1dVxzzTUsWbKE22+/PYiyZZwyxgRdgohnyrG4QlkWF/iRYzVGJCt0JbuCLkHEsy2xLSf8mG1tbSxfvpyDBw8O+x7grbfe4sorr6S2tpba2lpmzZpFTU0Nt9xyC88//zz79+/n1VdfPeG1y/gUjUaDLkHEM+VYXKEsiwv8yLEaI5IVCnP0KDLJfAuiC074MSdMmMDq1aspKioa9j3A66+/zpo1a7j44otZsWIFfX197Nmzh3POOQeA8vJy2tvbT3jtMj7ptG1xgXIsrlCWxQV+5Fg3X5UxZYzJAx4FTgHagKuB54EtwNnW2qoR9qsB/hTIBxqBa621fcaYdcDPgeuttWebgfOmHgZmpLa7xlp72CNo4p1xoqujdCY7CeeEmXHBDPbM2kNVWRV7u/cST8aZWTiTDS0bmFc8j5AJsb51PYtLF7P74G4ApudPZ23zWhaWLCRhE2yJbWFBdAG7OneRl5PHtPA01jStoaqsiva+dnZ27OT8kvPZ0bGDaCjK1Lyp6fUtiRZ2d+1m/uT5bG/fzpRJU6iYVJFe39DTwP6e/cyNzGVz22amF0wnGoqm1++L76Ml0cKcojlsbN3I7KLZRCZG0us1JzfnVB4qZ+lJS0/YnDo7O+nq6qK3t5f+/n7q6uoIh8Pk5uYSj8fp6uoiFotx8skn88QTT2CtpaamhqeffpoFCxZw5513cuaZZ7JmzRpuvfVW6urq0s+Z7+zspKKigsbGRowxRKNRGhsbiUQiJJNJurq6qKyspL6+nlAoRHFxMU1NTRQXF9Pb20t3d3d6fW5uLkVFRTQ3N1NSUkJ3dzfxeDy9Pi8vj3A4TGtrK6WlpXR0dNDb25tef2hOsViMsrIyYrEYiUQivb6goICcnBza29spLy+npaUFay3l5eU0NDRoTsc4p3g8Tnt7u1NzcvFz0pxGn1M8Hqenp8epObn4OWlOR54TQF1dnVNzcvFz0pxGn1M8HqehoWGkr6RHxVirey/I2DHGrAQKrLXfMsZcD7wFbAA+Za19apT9aoBea+1dxpgHgZettf9pjHkb+Ddr7f2p7ZYCS621y4wx9wHrrLXPDB3vh8/+0H5u6+f8n6DICfTxyR/nV22/OmHHG/xUmurqampra4d939PTw6RJkwB46KGHSCQS3HTTTWzatIkHHniAuXPncsstt5ywumV8a2pqoqysLOgyRDxRjsUVyrK44FCOt23btnXx4sXnHc8YupRGxtpMYHPq9aMMnCmyc7SmyCBbUz/fBKalXseAVYO2OQv4eOpMkgXAsM9qyjW5x1KzyLg0LTwt6BKGdeONN7Jz506SySTPP/88s2fPBmD27Nm89957LF++POAKZTzp6tI9nyTzKcfiCmVZXOBHjnUpjYy1XcA8YC3wt8ABoPMo950PrAHmAr9ILTtore0ftM3bwOPW2n8wxvwZDP/4mfY+3d9AMt+apjVBlzCsr33ta3zxi1/EWsull17KokWLAHjggQdYvnw5+fn5wRYo40plZWXQJYh4phyLK5RlcYEfOVZjRMba94B/T53R0Qx8OvXnaMxL7VcPPDvCNs8Alxlj1jPQFPnMcBtFJkaOoWSR8amqrIrH3n8skGMPvoxm6PtZs2YN+9SZ2267bczrksxTX1/P6aefHnQZIp4ox+IKZVlc4EeO1RiRMWWt7WbghquDLTrK3e+z1q4bMt6iIe/7gf99pIH66T/SJiLjns58EheEQqGgSxDxTDkWVyjL4gI/cqzGiAQudVbIYDFr7V/4eYzTik/7wI0kRTJRV1cXBQUFQZch4klxcXHQJYh4phyLK5RlcYEfOVZjRAI39CyQsdDX1zfWhxAZc01NTWqMSMZTjsUFyrG4QlkWF/iRYz2VRrJCTk5O0CWIeKZ/1REXKMfiAuVYXKEsiwv8yLEaI5IVrB32YTUiGaW3tzfoEkQ8U47FBcqxuEJZFhf4kWM1RiQr9Pfr5quS+bq7u4MuQcQz5VhcoByLK5RlcYEfOVZjRLKC7rgtLvDjGe0iQVOOxQXKsbhCWRYX+JFjNUYkKyQSiaBLEPGsvr4+6BJEPFOOxQXKsbhCWRYX+JFjNUYkK0yYoKhL5svNzQ26BBHPlGNxgXIsrlCWxQV+5FjfFiUrqDEiLigqKgq6BBHPlGNxgXIsrlCWxQV+5FjfFiUr9PX1BV2CiGfNzc1BlyDimXIsLlCOxRXKsrjAjxxP9KEOkXHvfzr+hwtXXRh0GSKezCyYya6uXWN6jJaVLWM6vkhJSUnQJYh4phyLK5RlcYEfOdYZI5IVQkZPpZHMN2XSlKBLEPFMj4YUFyjH4gplWVygx/WKHKWJRidHSearmFQRdAkinsXj8aBLEPFMORZXKMviAj9yrMaIZIX2vvagSxDxbE3TmhN2rAMHDrBkyZIR3w9evnDhwiNuJ3JIZWVl0CWIeKYciyuUZXGBHzlWYyTLGGPu97DvOh9LGTr2MmPMslHW1xhjFh3v+JGJkePdVWTcqCqrOiHHaWtrY/ny5Rw8eHDY94Pdcccd6S79aNuJHFJfXx90CSKeKcfiCmVZXOBHjtUYyTLW2puDriEIfVZPpZHM19DTcEKOM2HCBFavXp1+9NnQ94ds2LCB/Px8TjrppFG3ExksLy8v6BJEPFOOxRXKsrjAjxzrxgsZxhhTCPwUKAB2W2uvT53JsQU421pbldrusGWHlltrF6Ve/x3wlrX2Z8aY24DdwC+Gjn8Mtb0OLAF2AOcCjwB/CfwQOAnYYa39sjEmf+iyQWN8BPgucDkD+XwSyAEMsG6E+f8j8Ftr7ePGmBpgl7X28cG1JToTRFdH6Ux2Es4JM+OCGeyZtYeqsir2du8lnowzs3AmG1o2MK94HiETYn3rehaXLmb3wd0ATM+fztrmtSwsWUjCJtgS28KC6AJ2de4iLyePaeFprGlaQ1VZFe197ezs2Mn5Jeezo2MH0VCUqXlT0+tbEi3s7trN/Mnz2d6+nSmTplAxqSK9vqGngf09+5kbmcvmts1ML5hONBRNr98X30dLooU5RXPY2LqR2UWziUyMpNdrTm7O6ayCs4hMjIztnBoaCIfDtLa2kkwmef/99+nt7aWyspJ4PM6BAwfIzc2lqamJu+++m29/+9usWLGCnp4eWltbKSgooK+vj7q6OsrLy2lpacFaS3l5OQ0NDRQWFgLQ2dlJRUUFjY2NGGOIRqM0NjYSiURIJpN0dXVRWVlJfX09oVCI4uJimpqaKC4upre3l+7u7vT63NxcioqKaG5upqSkhO7ubuLxeHp9Xl5eek6lpaV0dHSk51RfX084HCY3N5dYLEZZWRmxWIxEIpFeX1BQQE5ODu3t7ZqTD3OKxWKEw2Gn5uTi56Q5jT6nzs5OJk+e7NScXPycNKcjz6m3t5e6ujqn5uTi56Q5jT6nWCx2lN9YR2astZ4HkRPHGHMmMAN4CfglcC1QB3zKWvvUoO3iQ5ellg9ujMwAvmqtvcEY8wsGmhhTho5vrW0Yuu8Itf0EqAWuZqB5cSbQBEy21tYYY54CaoCLhln2v4CTgWuAT1hr640xXwd6rLX3G2NeBO4E9g0z/0LgX6y1lxtjfgVcZK39wK2JH3/ucXvd69cdza9YZNy67uTreOz9x8b0GIMf11tdXU1tbe2w7++55x5mzJjB0qVLR91OZKi6ujpOP/30oMsQ8UQ5Flcoy+KCQznetm3b1sWLF593PGPoUprMkwC+APwYiAJhYOfQBsgIyz7AWvs74BRjTARos9Z2jTD+0drGQFPkOeAqYCtwFnBF6gyWM4CpIywDuAl4Dzj0t/OHgDdSr19P/TysPmvtHqAodQ+SnUObIgAHk7rngWS+zW2bgy4hbf369TzyyCNUV1ezY8cOVq5cGXRJkiFKS0uDLkHEM+VYXKEsiwv8yLEaI5nnrxg4G+M6oCu1rHOY7YZbNpzNwM3AM6OMf7S2M3A2yEtAFQONkreB+1NnmtwOvDPCMoB/Ar6U+klq+UdSr889Qn2PA6sZuETnMJMmTDrGqYiMP9MLpgddQtpzzz1HbW0ttbW1zJkzh1WrVgVdkmSIjo6OoEsQ8Uw5Flcoy+ICP3KsxkjmeRG4DXg59X7qKNsejScZaIw868P42xi4rOcPwAFrbR3wPeBSY8wG4Ebg3RGWAcStte8Cu4wxlwMPA1emziw59FiZker7KWCBV4crLMfkHMM0RManaCh6Qo839HKYkS6POdrtRAB6e3uDLkHEM+VYXKEsiwv8yLHuMSIZL3XD1h8AD1lrHxlum9dee83OmjXrxBYm4rOenh4mTdLZT5LZlGNxgXIsrlCWxQWHcqx7jMgJZ4xZN+TPz4OqxVr7lrV2/khNEYBEInEiSxIZE348o10kaMqxuEA5Flcoy+ICP3Ksx/XKcRnt6TTj0YQJ6gFK5guHj+VeyCLjk3IsLlCOxRXKsrjAjxzr26JkBWNM0CWIeJabmxt0CSKeKcfiAuVYXKEsiwv8yLEaI5IVkslk0CWIeBaLxYIuQcQz5VhcoByLK5RlcYEfOVZjRLLCxIm6akwyX1lZWdAliHimHIsLlGNxhbIsLvAjx2qMSFbQGSPiAv2rjrhAORYXKMfiCmVZXKAzRkSOkh5LLS7Q05ACZaIAACAASURBVJXEBcqxuEA5Flcoy+ICP3KsxohkhVAoFHQJIp5VVlYGXYKIZ8qxuEA5Flcoy+ICP3KsxohkBXXDxQV+PKNdJGjKsbhAORZXKMviAj9yrMaIZIWcnJygSxDxrKCgIOgSRDxTjsUFyrG4QlkWF/iRYz2qQ7LCnrY9LFi1IOgyRDyZWzSX7R3bx/QYLStbxnR8ETWqxQXKsbhCWRYX+JFjnTEiWSFvQl7QJYh4NrNwZtAliHjW3t4edAkininH4gplWVzgR47VGJGs0JnsDLoEEc82tGwIugQRz8rLy4MuQcQz5VhcoSyLC/zIsRojkhUKcnT9pGS+ecXzTtixDhw4wJIlS0Z8P3j5woUL0+9XrFjBJZdcwr333ntC6pTM09Kiy7Uk8ynH4gplWVzgR47VGMlAxph1Yzj2ucaYcz3sf7+f9fjFYIIuQcSzkDkxj51ua2tj+fLlHDx4cNj3g91xxx3E43EAamtr6e/v54UXXmDv3r3s2bPnhNQrmcVaG3QJIp4px+IKZVlc4EeO1RiRoc5N/Tku1tqbfazFNx3JjqBLEPFsfev6E3KcCRMmsHr1aoqKioZ9f8iGDRvIz8/npJNOAuC1115j6dKlAFx44YVs2rTphNQrmUWnbYsLlGNxhbIsLvAjx3oqTQYzxkwCHgWmAO8B1wMbgSXADgYaHI8Afwn8EDgJ2GGt/bIxJgw8CUSAZuAq4J+AK1Jjf9Zau9gYUwP8KZAPNALXWmv7Umet/By43lp79qCa1llrF6VeG+C7qToSwLVAA/AwMCM13jXW2uQwc1sGfC71the42lobSx33IeA24BJrbb0x5h+BxUDXoe2GjheOh4mujtKZ7CScE2bGBTPYM2sPVWVV7O3eSzwZZ2bhTDa0bGBe8TxCJsT61vUsLl3M7oO7AZieP521zWtZWLKQhE2wJbaFBdEF7OrcRV5OHtPC01jTtIaqsira+9rZ2bGT80vOZ0fHDqKhKFPzpqbXtyRa2N21m/mT57O9fTtTJk2hYlJFen1DTwP7e/YzNzKXzW2bmV4wnWgoml6/L76PlkQLc4rmsLF1I7OLZhOZGEmv15zcnNOK01awtX3r2M6poYFwOExrayvJZJL333+f3t5eKisricfjHDhwgNzcXJqamrj77rv59re/zYoVK+jp6aGhoYG8vDxaW1tJJBLs27eP9957D2st5eXlNDQ0UFhYCEBnZycVFRU0NjZijCEajdLY2EgkEiGZTNLV1UVlZSX19fWEQiGKi4tpamqiuLiY3t5euru70+tzc3MpKiqiubmZkpISuru7icfj6fV5eXnpOZWWltLR0ZGeU319PeFwmNzcXGKxGGVlZcRiMRKJRHp9QUEBOTk5tLe3U15eTktLi+bkYU5/+MMfmDZtmlNzcvFz0pxGn1NTUxNnnXWWU3Ny8XPSnI48p/r6evLz852ak4ufk+Y0+px+97vfUVFRMfQr4DExOn0q8xxqPhhjbgKKrbV3phoY9cBFQC1wNfBT4EygCZhsra0xxjwF1AAh4B+stZcbYy4HNlhr21INCay1j6aOVQP0WmvvMsY8CLxsrf1PY8zbwL9Zaz9w6cyQxsjlwGXW2huMMX8O2NRxl1prlxlj7gPWWWufGWaOy4DzrbVfNMZ8Dei31n471RjZBNxmrbWpy37+xVp7oTFmZar2VUPH+/faf7fLti075t+1yHgyr3geW2JbxvQYgx/XW11dTW1t7bDv77nnHmbMmMHSpUvTy7/xjW9w5ZVXMm/ePGpra/n973/P3/zN34xpvZJ5mpubKS0tDboMEU+UY3GFsiwuOJTjbdu2bV28ePF5xzOGLqXJbLOA/0693gR8GNjGQFPkOQbOAtkKnAVckWoqnAFMTW230xjzAlAFHH7zgD/amvr5JjAt9ToGHNaAGGImsBnAWvss8ItULR9P1bIAGK21N9xxAb5p/9jROws4IzXepwD9zS5yAqxfv55HHnmE6upqduzYwcqVKzn33HPTl8/s3LmT0047LeAqRURERESOTJfSZLa3gI8BL6V+vgXUAX8PfAV4APgycDqw2Vr7g9SZG+8A5wCvWWv/1hjz/wEXAGuBblLNhdSlMADzgTXAXAaaGwAHrbX9R6hvFwOX9TxijPk0A42cLcDj1tp/MMb8GQNnkYxkPgOXzcwFdh9aaK0d/Ozdtxk46+RzxpjZqbkeZtKESUcoVWT8m54/fczPGDlazz33XPp1dXU1q1ator29ncsuu4z6+npeeuklXnzxxQArlPGqs7NT/zopGU85Flcoy+ICP3KsM0Yy2/eBjxhjNjBwycyjDJwJUgf8AThgra0DvgdcmtruRuBdYC+w0hizEagEXk+N+SLwSWPMaww0SwDmpc7ImAw8ewz11QI2ddzPAvcDzwBTjDHrgW+mah3JqcaYV4CFwOrhNrDW/hp4NzXe91JzO4xuviouWNu89oQeb/BlNMO9H7o8EolQW1vLeeedxzPPPEMkEhnzGiXzeL0GWGQ8UI7FFcqyuMCPHOseIzKq1D1G1llr153g4y6DP97rxKv169fbs88++8gbioxj7777LqeeemrQZYh4ohyLC5RjcYWyLC44lGMv9xjRpTQyKmttzVgfwxjzOANnrQx2qbW2e6yPLZJJ/nh1m0jmUo7FBcqxuEJZFhf4kWM1RiRw1tprx/oYEycq6pL5otFo0CWIeKYciwuUY3GFsiwu8CPHuseIZIVEIhF0CSKeNTY2Bl2CiGfKsbhAORZXKMviAj9yrMaIZIWcnJygSxDxTDczFRcox+IC5VhcoSyLC/zIsRojIiIZIplMBl2CiGfKsbhAORZXKMviAj9yrMaIZAX9pS8u6OrqCroEEc+UY3GBciyuUJbFBX7kWI0RyQqhUCjoEkQ8q6wc+vAmkcyjHIsLlGNxhbIsLvAjx2qMSFbQzVfFBfX19UGXIOKZciwuUI7FFcqyuMCPHKsxIllBz2gXF+jMJ3GBciwuUI7FFcqyuMCPHKsxIllBT6URFxQXFwddgohnyrG4QDkWVyjL4gI/cjzRhzpExr33Yu9xwaoLgi5DxJPrTr6Ox95/zLfxWla2+DaWyNFqamqioKAg6DJEPFGOxRXKsrjAjxzrjBHJCt393UGXIOLZjo4dQZcg4pn+dVJcoByLK5RlcYEfOVZjRLLCRKOToyTzRUPRMRn3wIEDLFmyZMT3Iy07tHzhwoVjUpe4qbe3N+gSRDxTjsUVyrK4wI8cqzESEGPM/Zl2XGPMOh9LGTr2MmPMMh/GqTHGLBq6PGR0YynJfFPzpvo+ZltbG8uXL+fgwYPDvh9p2SF33HEH8Xjc97rEXd3dOoNPMp9yLK5QlsUFfuRYjZGAWGtvzqbjBq29rz3oEkQ8W9O0xvcxJ0yYwOrVqykqKhr2/UjLADZs2EB+fj4nnXSS73WJuyorK4MuQcQz5VhcoSyLC/zIsa4vCIgxZp21dlHqdRh4EogAzcBV1tq+YfYpBH4KFAC7rbXXHxoL2AKcba2tGmnZMMf9O+Ata+3PjDG3AbuBXwx3jKOc0+vAEmAHcC7wCPCXwA+Bk4Ad1tovG2Pyhy4bNMZHgO8ClwPJYfatAULABanf1yeAntTvLwcwwLqhteX35BNdHaUz2Uk4J8yMC2awZ9Yeqsqq2Nu9l3gyzszCmWxo2cC84nmETIj1retZXLqY3Qd3AzA9fzprm9eysGQhCZtgS2wLC6IL2NW5i7ycPKaFp7GmaQ1VZVW097Wzs2Mn55ecz46OHURDUabmTU2vb0m0sLtrN/Mnz2d7+3amTJpCxaSK9PqGngb29+xnbmQum9s2M71gOtFQNL1+X3wfLYkW5hTNYWPrRmYXzSYyMZJerzm5OacVp61ga/tW3+bU3t5Od3c38Xic/v5+6urqyMvLIxwOE4/H6ezspKOjg97eXiorK4nH4xw4cIDc3Fyampq4++67+fa3v82KFSvo6emhvr6egoICcnJyaG9vp7y8nJaWFqy1lJeX09DQQGFhIQCdnZ1UVFTQ2NiIMYZoNEpjYyORSIRkMklXVxeVlZXU19cTCoUoLi6mqamJ4uJient76e7uTq/Pzc2lqKiI5uZmSkpK0nM6tP7QnFpbWyktLf3AnOrr6wmHw+Tm5hKLxSgrKyMWi5FIJNLrNSd/5/SHP/yBadOmOTUnFz8nzWn0OTU1NXHWWWc5NScXPyfN6chzqq+vJz8/36k5ufg5aU6jz+ntt9+moqLiCN9WR2estZ4GkOMzpEHxUeAfrLWXG2MuBzZYa9uG2edMYAbwEvBL4FprbYMxJg58ylr71KBtD1s2zHFnAF+11t5gjPkFA02MKcMdY+i+I8zpJ0AtcDUDzZUzgSZgsrW2xhjzFFADXDTMsv8FnAxcA3zCWltvjLl5mO0+CXzYWnuNMeYOBpo5pwI91tr7jTEvAndaa9cNru3Hz/7YfmbrZ0YqXSQjVJVV+XrWyOCn0lRXV1NbWzvi+6HL7rnnHmbMmMHSpUuH3VZkJO+//z4nn3xy0GWIeKIciyuUZXHBoRxv27Zt6+LFi887njF0Kc34sA3YaYx5AagCDr+Qf0AC+ALwYyAKhFPLdw5tgIyw7AOstb8DTjHGRIA2a23XKMc42nlcDTwHXAVsBc4CrkidwXIGMHWEZQA3Ae8Bp6fej7TdD1M/3wFygQ8Bb6SWvT5cYT39PccwDZHxaXfX7qBLSFu/fj2PPPII1dXV7Nixg5UrVwZdkmSIoZdkiWQi5VhcoSyLC/zIsRoj48M5wGvW2kuAEgYuExnOXzFwJsZ1QNeg5Z3DbDvcsuFsBm4GnjnCMY7GdgbOBnmJgQbPNuBt4P7UmSa3M9DMGG4ZwD8BX0r9ZJTthtb1DvCR1OtzhyssPyf/GKciMv7Mnzw/6BLSnnvuOWpra6mtrWXOnDmsWrUq6JIkQzQ3NwddgohnyrG4QlkWF/iRYzVGxoe9wEpjzEagkhHOegBeBG4DXk699+MRFU8y0Bh51odjbAPqgD8AB6y1dcD3gEuNMRuAG4F3R1gGELfWvgvsSl1SNNJ2Qz0MXJk6syQy3Abd/brjtmS+7e3bx2zsoZfCDHdpzEiXy+gyGjkWJSUlQZcg4plyLK5QlsUFfuRY9xiRrPCjZ39kP7v1s0GXIeLJRdGLeLnl5SNveJQG32NE5ERpaGjwfIM0kaApx+IKZVlccCjHXu4xoqfSjFOpsx8Gi1lr/yKIWoYz3usb6pTCU/QlUDJeXV0dp59++pE3FBnH4vF40CWIeKYciyuUZXGBHzlWY2ScGu3pL+PBeK9vqFAoFHQJIp758Yx2kaApx+IC5VhcoSyLC/zIse4xIlkhkUgEXYKIZ/X19UGXIOKZciwuUI7FFcqyuMCPHKsxIllhwgRFXTJfXl5e0CWIeKYciwuUY3GFsiwu8CPH+rYoWUGNEXFBOBwOugQRz5RjcYFyLK5QlsUFfuRY3xYlK/T19QVdgohnra2tQZcg4plyLC5QjsUVyrK4wI8cqzEiWWHiRN1nWDJfaWlp0CWIeKYciwuUY3GFsiwu8CPHaoxIVujv7w+6BBHPOjo6gi5BxDPlWFygHIsrlGVxgR85VmNEsoIaI+KC3t7eoEsQ8Uw5Fhcox+IKZVlc4EeO1RiRrBAKhYIuQcQzP57RLhI05VhcoByLK5RlcYEfOVZjRLJCIpEIugQRz/x4RrtI0JRjcYFyLK5QlsUFfuRYd6SUrPBu57tcuOrCoMsQ8WRByQI2tG444nYtK1tOQDUix0ePhhQXKMfiCmVZXKDH9YocpT6rx/VK5mtJqOEhmS83NzfoEkQ8U47FFcqyuMCPHKsxIlkhPEHdcMl8c4rmHNP2Bw4cYMmSJen3K1as4JJLLuHee+8FoK+vjzlz5lBdXU11dTW/+c1vaGtr4+qrr+aiiy7iK1/5iq/1iwDEYrGgSxDxTDkWVyjL4gI/cqzGiOOMMTXGmEUB1/BhY8zPg6yhK9kV5OFFfLGxdeNRb9vW1sby5cs5ePAgALW1tfT39/PCCy+wd+9e9uzZw1tvvcWVV15JbW0ttbW1zJo1iyeeeIKrrrqKl19+mc7OTrZv3z5W05EsVVZWFnQJIp4px+IKZVlc4EeO1RiRMWWM+RPgn4HiIOsI5+iMEcl8s4tmH/W2EyZMYPXq1RQVFQHw2muvsXTpUgAuvPBCNm3axOuvv86aNWu4+OKLWbFiBX19fUSjUX77298Si8XYt28fU6dOHZO5SPbSv06KC5RjcYWyLC7wI8e6+WqGMcZMAh4FpgDvAdcDLwBbgLOttVXGmBLgSSAHMMA6Y0w+8EPgJGCHtfbLqfHWDdm3BggBFwAR4BPAjcA6a+06Y8yyVCkrgANAL1AJ/MBa+3+HKbkDuBJYc4R5/Tvwb9baTcaYR4H/C/xPaq7FQK219lvGmCnATwALbLDW/p0xZhpwZ6oWrLXXDx2/v6uf6OoonclOwjlhZlwwgz2z9lBVVsXe7r3Ek3FmFs5kQ8sG5hXPI2RCrG9dz+LSxew+uBuA6fnTWdu8loUlC0nYBFtiW1gQXcCuzl3k5eQxLTyNNU1rqCqror2vnZ0dOzm/5Hx2dOwgGooyNW9qen1LooXdXbuZP3k+29u3M2XSFComVaTXN/Q0sL9nP3Mjc9nctpnpBdOJhqLp9fvi+2hJtDCnaA4bWzcyu2g2kYmR9HrNyc05faz4Y4RM6Ihz6urqorW1leLiYnp7e6mrq6OjowNrLe+//z7hcJg333yTiy++mIcffphIJMKdd97Jj3/8Y+bMmcNzzz3H3XffzYc+9CHi8Th1dXVUVlZSX19POBwmNzeXWCxGWVkZsViMRCKRXl9QUEBOTg7t7e2Ul5fT0tKCtZby8nIaGhooLCwEoLOzk4qKChobGzHGEI1GaWxsJBKJkEwm6erqSo8ZCoUoLi6mqakpPafu7u70+tzcXIqKimhubqakpITu7m7i8Xh6fV5eHuFwmNbWVkpLS+no6KC3t1dzCmhOTU1NFBYWOjUnFz8nzWn0OTU1NVFaWurUnFz8nDSnI89p6JguzMnFz0lzGn1OTU1N5OTkjPZ184iMtdbTAHJiGWNuAoqttXemmhj1wP3Ap6y1T6W2+TrQY6293xjzIgNNg3OBydbaGmPMU0CNtfZNY0x8yL41wIettdcYY+4AdgMzOLwx8nVgHrADuBi4fbiGxKC611lrF42yfjGwFPgq8F/W2j81xtwP/Npa+6gx5r+BJcAZwCTg18BGa+3ZqcbIm8Al1tpNw43/8M8ftjf8+oaRDi+SEaKh6FHdgHXwU2mqq6upra3lG9/4BldeeSXz5s2jtraW3//+93z5y19m0qRJADz00EMkEgl27drFXXfdRSQS4cEHH6SgoIBly5aN1ZQkC/X09KRzJ5KplGNxhbIsLjiU423btm1dvHjxecczhi6lyTyzgP9Ovd4EfBjYeaixkfIh4I3U69dTP88CrkidIXIGcOj8+KH7wsCZJQDvAENv8XvompQGa20nUAckGTgzxYtXgI8DlwHPDKr5S6maCxg4S6YP+AbwfaBo0P4vjNQUAYhMjHgsTyR4VWVVx73vueeey6ZNA/+J7Ny5k9NOO40bb7yRnTt3kkwmef7555k9ezaxWIzf/OY3JJNJtm7dijFe/9MW+aD6+vqgSxDxTDkWVyjL4gI/cqxLaTLPW8DHgJdSP98CzhmyzTvARxhoNpzLwGUsbwObrbU/MMb8eWobgM5hjjH0TqW9QHnq9SeApz3O4TDW2v7U2S33AhelFr8N/Nxa+4ox5jNAC/B/gG8x0Ph5c9AQw80jrdf2+l2yyAm3t3vvce+7ZMkSLrvsMurr63nppZd48cUXmTVrFl/84hex1nLppZeyaNEiioqKuOmmm3jvvfc477zzuPLKK/2bgAhQUFAQdAkininH4gplWVzgR47VGMk83wceNcZsAN4F7gI+NWSbh4EnjTF/ycD9QgC+B/zAGHM90D7MPqN5BvjX1OUuzV6KP4IngY9Za+tS7/8P8Igx5psM3G/kceBZBu4/0ggcNMYc1Z0h+23/GJQrcmLFk/Fj3qe2thaASCRCbW0tr7zyCitXriQSiTBr1ixeffXVD2z/0Y9+lF/96le+1CsyHK/XAIuMB8qxuEJZFhf4kWM1RjKMtbYHuG7I4kVDtmkCLhxm96uHGW/ovjWDXj86aNWCIbs+OmT/ZcNXPPxxhko1Xe4B/m7QPvUMXFoz2BOpP0ONevy8CXmjrRbJCDMLZ7K94/gfnzt58mSuuOIKHysSOXbt7e2UlJQEXYaIJ8qxuEJZFhf4kWM1RsQXxphKBs7oGOxta+0Nx7DdR8eqvlMnn/qBG1KKZKKDBw/yYP6DQZch4kl5efmRNxIZ55RjcYWyLC7wI8dqjIgvUmd3LPJrO7/19fWd6EOK+K6lpYX8/PygyxDxRDkWFyjH4gplWVzgR471VBoRkQyhx6uLC5RjcYFyLK5QlsUFfuRYjRHJChMn6uQoyXw63VVcoByLC5RjcYWyLC7wI8dqjEhWSCQSQZcg4llDQ0PQJYh4phyLC5RjcYWyLC7wI8dqjEhW0KPIxAWFhYVBlyDimXIsLlCOxRXKsrjAjxyrMSIiIiIiIiIiWUuNEckKyWQy6BJEPOvs7Ay6BBHPlGNxgXIsrlCWxQV+5FiNEckKoVAo6BJEPKuoqAi6BBHPlGNxgXIsrlCWxQV+5FiNEckKfX19QZcg4lljY2PQJYh4phyLC5RjcYWyLC7wI8d6hqlkhf2d+1m0alHQZYgMq2Vly1FtZ4wZ40pExp5yLC5QjsUVyrK4wI8c64wRyQpdya6gSxDxLBqNBl2CiGfKsbhAORZXKMviAj9yrMaIZIXCHD2KTDKfTncVFyjH4gLlWFyhLIsL/MixGiMOM8as87BvjTFm0aGfx3tMY0yxMeZlY8w6Y8wVxzqeX+L98RN9SJGjVldXxzXXXMOSJUu4/fbb08sPHDjAwoUL0+8jkchhy0QyTSQSCboEEc+UY3GFsiwu8CPHaozIWDsH2GitXWStfTqoIiYYRV3Gr5qaGm655Raef/559u/fz6uvvgrAHXfcQTz+x6ZeMpk8bJlIptHj08UFyrG4QlkWF/iRY31bzALGmEJjzC+NMf9ljPlBalmNMeZOY8wGY8yvjTGVxpgSY8xLxphXgEWDhvh/h2x32HgjHPevgVXAZ1JnjJSPMN4kY8xjxpj1xpgfG2NyB59ZYoxZZoxZlnq9zhjzz8aYNan3YWPMs6nxnjbGDHtD4VyT6+2XKDKG9uzZwznnnANAeXk57e3tbNiwgfz8fE466aT0dq+88sphy0QyTVeX7vkkmU85Flcoy+ICP3Ksp9Jkh5OBB4CXgF8aYw496Hm6tXaBMeYO4CLgVOBZa+39xpgXB+0/dLstQ8ez1jYMPai19jvGmDeARdbaGkjfMXjoeFFgp7X2OmNMDfD5UebyMWCVtfZrqfezgP7UeJcDhUDb0J26OrqIro7SmewknBNmxgUz2DNrD1VlVezt3ks8GWdm4Uw2tGxgXvE8QibE+tb1LC5dzO6Duwd+CfnTWdu8loUlC0nYBFtiW1gQXcCuzl3k5eQxLTyNNU1rqCqror2vnZ0dOzm/5Hx2dOwgGooyNW9qen1LooXdXbuZP3k+29u3M2XSFComVaTXN/Q0sL9nP3Mjc9nctpnpBdOJhqLp9fvi+2hJtDCnaA4bWzcyu2g2kYmR9HrNKbPm9PEFH+fOO+/kzDPPZM2aNdxyyy18+tOf5qGHHuJLX/oSdXV1lJSU8PDDD/Od73yHW265hbq6OiKRCMlkkq6uLiorK6mvrycUClFcXExTUxPFxcX09vbS3d2dXp+bm0tRURHNzc2UlJTQ3d1NPB5Pr8/LyyMcDtPa2kppaSkdHR309vam14fDYXJzc4nFYpSVlRGLxUgkEun1BQUF5OTk0N7eTnl5OS0tLVhrKS8vp6GhgcLCgfv9dHZ2UlFRQWNjI8YYotEojY2NmlMWzCmZTNLe3u7UnFz8nDSn0eeUTCbp6elxak4ufk6a05HnlJubS11dnVNzcvFz0pxGn1MymaSh4bCvo8fEWGs9DSDjlzFmnbV2kTFmGvAvQBI4E/gLYBmwxVr73KGzMRhoOjxhrX3FGPMtYA0DZ44M3W7d0PGstXsHH3NQDYv4YGOkZpjx5gNPWWtfMsZ8ArgUaAXWWWvXGWO+BHRbax81xrxurT1v0PgGuBM4D/g98BVrbe/Q38Xjzz1ur3v9umP8DYqcGC0rW9i0aRMPPPAAc+fOpb+/nxkzZrB06VKqq6upra3lnnvuIRqN8oUvfCG9TCQT1dXVcfrppwddhognyrG4QlkWFxzK8bZt27YuXrz4vCPvcThdSpMd/gr4KXAdMPg8o6HnHL0DfCT1+txRthtpvKM1dJ+3GGjKkPr5FtALHLr05hODtu0csu85wGvW2kuAEuCC4Q7YT/9xlCly4syePZv33nuP5cuXs379eh555BGqq6vZsWMHK1euZP369fzkJz/5wDKRTBQKhYIuQcQz5VhcoSyLC/zIsS6lyQ4vAv8K3Jh6P3WE7R4GnjTG/CUwWrqGG2+vh/q+DzxqjNkAvAvcBcwA/tUYsxhoHmXfvcDdxpi/A+LA68Nt1J3s9lCeyNh74IEHWL58Ofn5+Tz33HPp5dXV1axatQoYuH6yoKDgA8tEMk1xcXHQJYh4phyLK5RlcYEfOdalNJIVdCmNjGctK1uOajud7iouUI7FBcqxuEJZFhf4cSmNzhiRrDA1MvWov3yKjFf6Vx1xgXIsLlCOxRXKsrjAjxzrHiOSFXRmlLigt/ew+wqLZBzlWFygHIsrlGVxgR85VmNEskJ/v26+Kpmvu1v3ypHMpxyLC5RjcYWyLC7wI8dqjEhW0B23xQWVlZVBlyDimXIsLlCOxRXKsrjAjxyrYremQQAAIABJREFUMSJZIZFIBF2CiGf19fVBlyDimXIsLlCOxRXKsrjAjxyrMSJZYcIERV0yX25ubtAliHimHIsLlGNxhbIsLvAjx/q2KFlBjRFxQVFRUdAliHimHIsLlGNxhbIsLvAjx/q2KFmhr68v6BJEPGtubg66BBHPlGNxgXIsrlCWxQV+5FiNEckKEydODLoEEc9KSkqCLkHEM+VYXKAciyuUZXGBHzlWY0Sygh7XKy7QI/XEBcqxuEA5Flcoy+ICPa5X5CipMSIuiMfjQZcg4plyLC5QjsUVyrK4wI8c6/oCyQq/i/2OC1ddGHQZkmVaVrb4Op4fz2gXCZpyLC5QjsUVyrK4wI8c64wRyQqRiZGgSxDxzI9ntIsETTkWFyjH4gplWVzgR47VGJGs0Gf1VBrJfHl5eUGXIOKZciwuUI7FFcqyuMCPHKsxIhhj1o3h2OcaY871sP/9ftSRsAk/hhE5Zm1tbVx99dVcdNFFfOUrX6Guro5rrrmGJUuWcPvtt6e3W7FiBZdccgn33nvviGOFw+ETUbLImFKOxQXKsbhCWRYX+JFjNUZkrJ2b+nNcrLU3+1FEeIL+0pdgPPHEE1x11VW8/PLLdHZ2snLlSm655Raef/559u/fz6uvvkptbS39/f288MIL7N27lz179gw7Vmtr6wmuXsR/yrG4QDkWVyjL4gI/cqzGiKQZYyYZYx4zxqw3xvzYGJNrjHndGHOSMabBGHOyMeZ5Y0y+MeanxpgNxpgHU/uGjTHPppY9bYyZaIz5FvAN4BvGmLWp7WqMMb9IHeOnxpiJqeXrjDFfMca8OaSmdYNeG2PMg8aY11LbV6aWfW/QeDnDze1g8uAY/dZERheNRvntb39LLBZj37591NfXc8455wBQXl5Oe3s7r732GkuXLgXgwgsvZNOmTcOOVVpaesLqFhkryrG4QDkWVyjL4gI/cqyn0shg/xvYaa29zhhTA3we+ANQBWwGLgG2AV9MbVdjjHnKGHM2EAL6rbULjDGXA4XW2tuMMW8DWGsfHXSc/7LW3pVqqvwF8J/AyQOb2bNHqa8amGit/X+MMX8OfDR13JC1dqEx5j7gMuCZoTtO7J5IdHWUzmQn4ZwwMy6YwZ5Ze6gqq2Jv917iyTgzC2eyoWUD84rnETIh1reuZ3HpYnYf3A3A9PzprG1ey8KShSRsgi2xLSyILmBX5y7ycvKYFp7GmqY1VJVV0d7Xzs6OnZxfcj47OnYQDUWZmjc1vb4l0cLurt3Mnzyf7e3bmTJpChWTKtLrG3oa2N+zn7mRuWxu28z0gulEQ9H0+n3xfbQkWphTNIeNrRuZXTSbyMRIer3mND7mdODAAWbNmsXTTz/Nd7/7XU455RTmzp3LXXfdxRlnnMELL7zAihUrePLJJykpKeG9996jr6+P/fv3U1dXR2FhIQCdnZ1UVFTwzjvvEIlEiEajNDY2EolESCaTdHV1UVlZSX19PaFQiOLiYpqamiguLqa3t5fu7u70+tzcXIqKimhubqakpITu7m7i8Xh6fV5eHuFwmNbWVkpLS+no6KC3tze9PhwOk5ubSywWo6ysjFgsRiKRSK8vKCggJyeH9vZ2ysvLaWlpwVpLeXk5DQ0Nh82psbERY4zmlEVzqqur49RTT3VqTi5+TprT6HNqbW1l+vTpTs3Jxc9JczrynJqamsjNzXVqTi5+Tv8/e/ceH3V153/8dQwTMglJyJCQ/EAL7VK8FFqpxlpaAYmKlkK9VCpubb304s8LhZbd1q2rdFdsf1t1XVzbtSzK6nYLbVe7RqxURUCFFiWo4G2LLZGLCUkmzCQhl8lwfn/kmzTGJFzmG77Jmffz8eAxl++Zcz6HeT98OIfz/X41p/7nVFlZSWFhYT8/Iw/PWGtT6kCGPmPMemvtDGPMT4BHrbXPGGMuBC4C3gM+A6wBPg+soGOBZCpQD4wEbgGeApYCZwJ/BBZZa9uMMVfDXxZGvAWXzdbatcaYb9KxgHK3MWYLcLa19lBvtXnP/xaos9au8F6fAPwNHQs47wEjgAestct7znHVmlV2/svz/fjrEjli0QVRbrrpJu68807y8vK4//77ycnJ4ZRTTuG+++5jypQpLF68mO9973tcdtlllJaWUl5ezh//+Ee+/e1vf6C/yspKxo0bF8BMRPyjHIsLlGNxhbIsLujMcUVFxdaysrIzj6UPnUoj3b0OnO09P9t7vQ2YCTxDx86RCuBt4F5vweJW4F3gE8CL1toLgALgHK+fZiAbOk6F8d47y3ucAuz0nh/suSjSi7eAUq+vvwb+0atllVfLQuCN3j4Yb48fpmuRgRGLxXjjjTdIJpNs3boVYwyTJk1iz5493HDDDQCcfvrpXafP7Nixgw996EO99uXHPdpFgqYciwuUY3GFsiwu8CPHWhiR7v4d+JgxZiPwUWAlHQshlXScUrPfWlsJLAcu8tpdD+wGdgELjDGbgBLgZa/Pp4FLjTEv8pfFklLv2iEjgSeOor5ywHrjXgXcS8dpM2OMMRuAO7xaPyBvWN5RDCPin4ULF7Jo0SLGjx9PfX09l112Gffddx833HAD2dnZAHzuc5/jl7/8Jd///vf5zW9+wwUXXNBrX37co10kaMqxuEA5Flcoy+ICP3KsU2nkuPJOpVlvrV1/PMd95IlH7Fe2fuV4DilCdEH0iNseOHCA5557jqlTp1JcXNxrm/379zN69Gi/yhMJhHIsLlCOxRXKsrigM8epnEqji6/KcWWtXRLEuOPzxx/Vj1SR423kyJFccskl/bbJzMw8TtWIDBzlWFygHIsrlGVxgR851qk0khaSyWTQJYikLBaLBV2CSMqUY3GBciyuUJbFBX7kWAsjkhaGDdPmKBn6Ur0NmchgoByLC5RjcYWyLC7wI8daGJG0oB0j4gL9q464QDkWFyjH4gplWVygHSMiR0gXGRYXJBKJoEsQSZlyLC5QjsUVyrK4wI8ca2FE0kIoFAq6BJGU+XGPdpGgKcfiAuVYXKEsiwv8yLEWRiQtaDVcXODHPdpFgqYciwuUY3GFsiwu8CPHWhiRtJCRkRF0CSIpy8nJCboEkZQpx+IC5VhcoSyLC/zIsRZGRESGCC3wiQuUY3GBciyuUJbFBX7kWAsjkhZ0VxpxQTweD7oEkZQpx+IC5VhcoSyLC/zIsRZGJC3o4qvigqKioqBLEEmZciwuUI7FFcqyuMCPHA/zoQ6RQe/dA+/y2WWfDboMcVR0QfT4jBONkp2dfVzGEhkoyrG4QDkWVyjL4gI/cqwdI5IWDCboEkRSZq0NugSRlCnH4gLlWFyhLIsL/MixFkYkLTQkG4IuQRx24MAB5s2bx8yZM1m0aBHt7e1MnjyZOXPmMGfOHN54442utvv372f69OnHNI62u4oLlGNxgXIsrlCWxQV+5FgLIw4zxtzb43W+MWadMWa9MeaSY+xziTFmhi8FHn6skDFmtTHmd17dBd2OhY0xf/KeX22Mubq/vnIzcge4Wklnq1ev5vLLL2fdunU0Njby6quvctlll1FeXk55eTmnnXZaV9vbbruNlpaWYxqnurrar5JFAqMciwuUY3GFsiwu8CPHWhhxmLV2YY+3PgFsstbOsNY+FkRNR+ki4Clr7QXAWuCqbsduBf7PkXbUeqjV59JE/iISifDmm28Si8XYu3cvzzzzDGvXruW8887j5ptvpr29HYCNGzeSnZ3N6NGjj2mcESNG+Fm2SCCUY3GBciyuUJbFBX7kWBdfdZgxZr21dob3/FvANcBIY8xngcuBOLASGAPsAa6x1rYZY9YDLwEft9bO8nZq/ArIAAyw3hiTDTwMjAa2W2tv7Byzx2eXAJ8CsoEa4ArgS0CRtfZeY8x84ERr7Y971m+tfbzbyyLgZW+MU4CPA3/odvwTxph1QAkwz1q7432dHYTIgxEak42EM8JMPGci75z2DrMKZ7GreRctyRZOGXEKG6MbKc0vJWRCbKjfQNmoMnYe3AnAhOwJPFv3LNMLppOwCV6KvcS0yDTeanyLrIwsxofHs7Z2LbMKZxFvj7OjYQdTC6ayvWE7kVCEsVlju45HE1F2Nu3krJFnsS2+jTHDx1A8vLjreHVrNfta9zElbwpbDmxhQs4EIqFI1/G9LXuJJqJMzp3MpvpNTMqdRN6wvK7jmtPxndOJJ57Ik08+yV133cWYMWOYMWMGZWVlfOhDH+KWW27h5z//OXPnzmXp0qXcfffdfPe736WyspKcnBwyMjKIx+MUFRURjUax1lJUVER1dXXXf+QbGxspLi6mtraW5uZmIpEINTU15OXlkUwmaWpqoqSkhKqqKkKhEPn5+dTW1pKfn09bWxvNzc1dxzMzM8nNzaWuro6CggKam5tpaWnpOp6VlUU4HKa+vp5Ro0bR0NBAW1tb1/FwOExmZiaxWIzCwkJisRiJRKLr+NHOqaamBmOM5pRGc6qpqSEUCjk1Jxe/J82p/znF43FGjBjh1Jxc/J40p8PPKR6P09jY6NScXPyeNKf+51RTU9P1D5HHyuiCO+7qvjDivZ4BzLDWLvFe3wTkW2uXegsYVdbafzPGtABXWmsf9dp9F2j1FjKeBpYCpwMjrbVLjDGPAkusta/18tklQJu19k5jzP3AOuBp4D+ttXONMSuBH1hr/9zPPD4C/Br4lLU2YYx5ArgZeMhaO8M7jeZrwLlA50LLnd37WLVmlZ3/8vxj/asU6deV/3sld955J3l5edx///3k5ORw9dVXA/DAAw+QSCQ4ePAgEydO5OKLL2bOnDmUl5cf9TiVlZWMGzfO5+pFji/lWFygHIsrlGVxQWeOKyoqtpaVlZ15LH3oVJr0dhp/2XXxe+BU7/mOzoUNz4eBV73nL3uPJwOXeDtEPgKM7eOzAFu9x9eA8dbaONBqjBkBFB5mUWQ4HbtavuEtinwF2NDLZ35hrU0A7wKZPfvRxVdlIMViMd544w2SySRbt27lBz/4ATt27CCZTPLkk08yadIkNmzYwIoVK5gzZw7bt29nwYIFRz1OcXHxAFQvcnwpx+IC5VhcoSyLC/zIsRZG0tvrwNne87O91wCNPdq9C3zMe3669/g2cK+3I+VWr01vnwU4y3ucAuz0nj8BfBt48TA1PgSstNZ2LshcCMz1FmRO93aPADT114kuvioDaeHChSxatIjx48dTX1/PmjVruP7665k2bRqlpaXMmDGDNWvWdF2MdfLkySxbtuyox6mpqRmA6kWOL+VYXKAciyuUZXGBHznWNUbS278DK40xG4HdwJ19tPsZ8CtjzBeBkPfecuAhY8w1dFyr5Mp+xin1FjKq6FgQAfgfYBdQ2teHjDEXAZcAY7ydIo9Za6/sdny9tfbzh7sjDYBFp4zJwDnjjDPYvHnz+9574YUX+mx/LKfRABhjjulzIoOJciwuUI7FFcqyuMCPHGthxGHdry/ivV4PrO/2upWOa3Ic7nO1dFy/o6d5h/us5x5v7O7tDgAje6+8q81vgXA/x2d4jyu7vbeebnPs1JTsd0OJyJAQiUSCLkEkZcqxuEA5Flcoy+ICP3KshREZUJ0Xej0cY8wqOu4o091F1tpmP+qYkDeB6IKoH12JBKampkYXSJMhTzkWFyjH4gplWVzgR461MCKDgrX2ioHsPyMjYyC7Fzku8vLygi5BJGXKsbhAORZXKMviAj9yrIuviogMEclkMugSRFKmHIsLlGNxhbIsLvAjx1oYkbSg/+iLC5qadK0cGfqUY3GBciyuUJbFBX7kWAsjkhZCodDhG4kMciUlPS/DIzL0KMfiAuVYXKEsiwv8yLEWRiQtJBKJoEsQSVlVVVXQJYikTDkWFyjH4gplWVzgR461MCJpQfdoFxdo55O4QDkWFyjH4gplWVzgR461MCJpQXelERfk5+cHXYJIypRjcYFyLK5QlsUFfuRYCyOSFtrb24MuQSRltbW1QZcgkjLlWFygHIsrlGVxgR851sKIpAXtGBEX6F91xAXKsbhAORZXKMviAu0YETlC1tqgSxBJWVtbW9AliKRMORYXKMfiCmVZXOBHjof5UIfIoLevYR/Tl00PugxxRHRBNJBxm5ubAxlXxE/KsbhAORZXKMviAj9yrB0jkhbi7fGgS5A0UF9fz3PPPUddXd2A9O/HPdpFgqYciwuUY3GFsiwu8CPHWhiRtJA3LC/oEsQxBw4cYN68ecycOZNFixZx4MABrrjiCioqKpg7d+77LgK1f/9+pk9PfceSH/doFwmaciwuUI7FFcqyuMCPHGthxAHGmNONMacHXUd/jDHrB7DvfGPMb40xvzPGPGaMyezZJmmTAzW8pKnVq1dz+eWXs27dOhobG3n99de54447+M53vsPMmTN59dVXu9redttttLS0pDxmZuYHoi0y5CjH4gLlWFyhLIsL/MixFkbccLr3J139NXCPtfYCoAq4sGeD1kOtx70ocVskEuHNN98kFouxd+9ePvrRj1JaWsqmTZuoqKigtLQUgI0bN5Kdnc3o0aNTHjM3NzflPkSCphyLC5RjcYWyLC7wI8e6+OogYYzJAlYCJwIHgDeAJ621640xV3vNVgO/AvKAOuBy4B+BS7w+rrLWlhljhnt9jQH2ANcAm4H9QBtQAjwEPOa1ywfKrbU/NMaMB5Z67bDWXmOMKe6l3XLgfmvtK8aYB4B/B/YCvwQssNFa+/2jmP9Kb17FwDZr7U3e++uBl4CPW2tnGWOygYeB0cB2a+2N1tqfdOuqyJvn+2S2ZBJ5MEJjspFwRpiJ50zkndPeYVbhLHY176Il2cIpI05hY3QjpfmlhEyIDfUbKBtVxs6DOwGYkD2BZ+ueZXrBdBI2wUuxl5gWmcZbjW+RlZHF+PB41tauZVbhLOLtcXY07GBqwVS2N2wnEoowNmts1/FoIsrOpp2cNfIstsW3MWb4GIqHF3cdr26tZl/rPqbkTWHLgS1MyJlAJBTpOr63ZS/RRJTJuZPZVL+JSbmTyBuW13VccxrYObW2tnLiiSfy+OOPs2zZMsaMGUMoFGLfvn08/PDD5OXl8d577xGPx/nRj37EP/3TP/G3f/u37Nu3j0QiQUlJCVVVVeTk5JCRkUE8HqeoqIhoNIq1lqKiIqqrqxkxYgQAjY2NFBcX8+c//5mCggIikQg1NTXk5eWRTCZpamrq6jMUCpGfn09tbS35+fm0tbXR3NzcdTwzM5Pc3Fzq6uooKCigubmZlpaWruNZWVmEw2Hq6+sZNWoUDQ0NtLW1dR0Ph8NkZmYSi8UoLCwkFoulNKeamhqMMZpTGs3pT3/6E+PHj3dqTi5+T5pT/3Oqra3l5JNPdmpOLn5PmtPh51RVVUV2drZTc3Lxe9Kc+p/Tn/70J4qLi4/0p2evjG5jOjgYYxYAOd6iwzV0LHr8U4+Fke3A7dbaucaYuXQsPhzoPG6tXen1dROQb61daoxZQscuim8BpV4f5wG3AjHgFWvtSmPMH4DPAbnAa8AF1trfe/3d20u7M4FPevVusNZON8aUAsOBV4BN1tqPd5vfemvtjH7mvxL4nbX2v4wxa4DbrLVbjTEtwJXW2ke9dguBkdbaJcaYR4El1trXvGOfBu6w1pb17P+h8ofstRXXHslXIXJY0QVRbrrpJu68807y8vK4//77ycnJ4eqrrwZg6dKlnHrqqezcuZOJEydy8cUXM2fOHMrLy1MaNx6Pk5en6+XI0KYciwuUY3GFsiwu6MxxRUXF1rKysjOPpQ+dSjN4nAJs8Z6vpGOXRKew91gB7DDG/A6YBRzso6/TgD94z38PnApUW2sbgUogCRjgZOD/ersycujYYQIdCxS/79Zfb+2eBT5ljDkVeNlr1w58j47dI8eyn2mr9/gaMN57vqNzUaRbLZd4tXwEGAtgjIkA9wG9rn6ETOgYyhHpWywW44033iCZTLJ161ZisRirVq0COv7jnJ+fz4YNG1ixYgVz5sxh+/btLFiwIKUxdUs9cYFyLC5QjsUVyrK4QLfrdctbdOzoAPg74BAdp4XAX66Z8QngRe9aGgXAOd77zUA2gDHGAK8DZ3vHzvZe9+Zt4HveTo4fAVHv/cbDtbPWtgM1wHzg1167bwM/BL5Gx+k0R+ss7/F04J1+arnXq+VW4F3vYqu/Am6x1lb21vEwo7PGxF8LFy5k0aJFjB8/nvr6ei677DJWr17N7NmzSSaTzJw5kzVr1lBeXk55eTmTJ09m2bJlKY3pxwVcRYKmHIsLlGNxhbIsLvAjx/q1OHgsB/7D2wlRB9wO/MQYU+a9BtgF/D9jzPeBFv6yU+Np4JfGmL8GbqFjx8ZKY8xGYDdwJ3BlL2P+CFhhjLkD+DOwio5rnBxJO+i4Rsm9Xq0ATwD/RseCyUFjzFhr7d6j+Dv4vDHmemCLtfaVPtosBx7yTjeKe/O6Dvgk8H3v7+an1trV3T8Ub48fRRkih3fGGWewefPm97332GOP9dk+1dNowJ97tIsETTkWFyjH4gplWVzgR451jREZFLxrjCyx1u4aiP5XrVll5788fyC6ljQUXRA9fKMBUFlZybhx4wIZW8QvyrG4QDkWVyjL4oLOHKdyjRHtGJHjyhhTwl92nHR621p79UCOOyZ3TGA/ZkX8kpWVFXQJIilTjsUFyrG4QlkWF/iRYy2MyHFlra0CZhzvcU84QZfTkaEvHA4fvpHIIKcciwuUY3GFsiwu8CPH+rUoaaG9vT3oEkRSVl9fH3QJIilTjsUFyrG4QlkWF/iRYy2MSFoYNkybo2ToGzVqVNAliKRMORYXKMfiCmVZXOBHjrUwImnh0KFDQZcgkrKGhoagSxBJmXIsLlCOxRXKsrjAjxxrYUTSghZGxAVtbW1BlyCSMuVYXKAciyuUZXGBHznWwoikhVAoFHQJIinz4x7tIkFTjsUFyrG4QlkWF/iRYy2MSFpIJBJBlyCSsqqqqqBLEEmZciwuUI7FFcqyuMCPHGthRNKCbtcrLtAt9cQFyrG4QDkWVyjL4gLdrlfkCBljgi5BJGWZmZlBlyCSMuVYXKAciyuUZXGBHznWPUwlLeyN72XasmlBlyGDSHRBNOgSjlosFmPkyJFBlyGSEuVYXKAciyuUZXGBHznWjhFJC03JpqBLEElZYWFh0CWIpEw5Fhcox+IKZVlc4EeOtTAiaSGcofMn5f0efPBB5syZw5w5c5g2bRqLFi0CYP/+/UyfPr3fNkGJxWKBji/iB+VYXKAciyuUZXGBHznWwoikhRMUdenh2muvpby8nPLycj796U/zla98BYDbbruNlpaWftsERXdXEhcox+IC5VhcoSyLC/zIsX4tDlLGmCXGmBkpfP5eH8s5ZsaY8anMwy/x9njQJcggtW/fPvbv38+UKVPYuHEj2dnZjB49us82QfLjHu0iQVOOxQXKsbhCWRYX+JFjLYw4ylq7MOgaPOOBGQHXQN6wvKBLkEFqxYoVXHvttbS1tXHXXXdx++2399kmaH7co10kaMqxuEA5Flcoy+ICP3Ksu9IMbt82xvwAeA94Gkhaa1d6OzBmAD8AHgbGAQngUmttDMAYs95aO8N7fjXwCe9PCTAPeB34GTARqAG+BBzq2R8Q720MY8x64H+Aa6y1HzfGZACPeO1qgS8CNwDXACO9mi/3jr1vXGttsufEvZq/6r1sA+Z1G/cB4BbgAmttlfd3VAY0dbbr2V9rYyuRByM0JhsJZ4SZeM5E3jntHWYVzmJX8y5aki2cMuIUNkY3UppfSsiE2FC/gbJRZew8uBOACdkTeLbuWaYXTCdhE7wUe4lpkWm81fgWWRlZjA+PZ23tWmYVziLeHmdHww6mFkxle8N2IqEIY7PGdh2PJqLsbNrJWSPPYlt8G2OGj6F4eHHX8erWava17mNK3hS2HNjChJwJREKRruN7W/YSTUSZnDuZTfWbmJQ7ibxheV3HNafDz6myspKMjAw2bNjAVVddxY9+9CO++MUvcuDAAQ4dOkRlZSWZmZnk5OTwzDPPsGDBAqqrq2lpaaGkpISqqiqysrIIh8PU19czatQoGhoaaGtr6zoeDofJzMwkFotRWFhILBYjkUh0Hc/JySEjI4N4PE5RURHRaBRrLUVFRVRXVzNixAgAGhsbKS4uprm5mT179hCJRKipqSEvL49kMklTU1NXn6FQiPz8fGpra8nPz6etrY3m5uau45mZmeTm5lJXV0dBQQHNzc2BzqmmpgZjjOaURnM6ePAg8XjcqTm5+D1pTv3P6eDBg7S2tjo1Jxe/J83pyOZUWVnp3Jxc/J40p77ndPDgQaqrq3v+BDwqxlqbUgcyMIwxS4BD1tp/MMY8ALwJHOixMHIfsA44HZgO/Mla+673+Z4LI18DzgXmAycCbwAXW2uvNsbcA6wHXuzZHx2LDR8YwxjzNvBTa+293hijgfOB1cBDwL9aa//QWau1donX7uKe41prH+9l/lcDU6213zDG/I33d3G3tzDye+AWa601xpwO/LO19lxjzAIAa+2ynv2tLF9pr6m45ii+AXFddEGUF198kSeeeIIf/vCHzJ49mxNO6NhEt337dubOncuyZcve1yZo9fX1FBQUBF2GSEqUY3GBciyuUJbFBZ05rqio2FpWVnbmsfShHSOD2x+8xwpgRLf3wwDW2jpjzErgKaAK6O/0mV9YaxPGmHeBjwAnA5/2FhpGAG/21p+1tr6PMWJA9wWIBPB5OnaKjO6ssRcfGLefmrd6j695fXe6w/5lRe9k4CNef1nA2t46yjohq59hJF2tW7eOqVOnArBmzZqu9+fMmcOyZcs+0CZo8Xhc//MiQ55yLC5QjsUVyrK4wI8c6xojg9sZ3uPH6ViUKPJeXwRgjDkJqLPWzgL20nHqS1+aerx+G1jl7SpZCLzRW3/9jHHQWnuoW3+XAju8x73d3m8Gsr16TW/j9lPzWd7jFGBn55vW2sYe8+jcHfM1YEtvHTUmG3t7W9Lc3//93zNOFt2IAAAgAElEQVRnzpwPvF9eXn7YNkEoKio6fCORQU45Fhcox+IKZVlc4EeOtTAyuJ1jjNkAFAMbgDnGmPuBDO94lffei8BM4Jmj6PtxYIzX/x1AZR/9HekYL9JxnZIXgAgw1nt/G3CyMeZ573hv4/blJGPMc3ScwvNgbw2sta8Au73+lgO7e2uXk5HTzzAiQ0M0Gg26BJGUKcfiAuVYXKEsiwv8yLFOpRmkOq/J0cO0Xt67vI/Pz+j2fGW35+vpuJ4IwNePsL8PvNe9f+/1W3TsbOnZrg34Qo+3exu3N//VvfbexvXeu/VwHY0ZMYboAv2HX4Y2XRNKXKAciwuUY3GFsiwu8CPHWhiRwBljVtFxt5zuLrLWNvs1xrBhiroMfdruKi5QjsUFyrG4QlkWF+hUGnGCtfYKa+2MHn98WxQBSCQSfnYnEohUb0MmMhgox+IC5VhcoSyLC/zIsRZGJC1kZGQcvpHIINd5T3iRoUw5Fhcox+IKZVlc4EeOtTAiIiIiIiIiImlLCyOSFpLJZNAliKSssVG3nZahTzkWFyjH4gplWVzgR461MCJpIRQKBV2CSMqKi4uDLkEkZcqxuEA5Flcoy+ICP3KshRFJC+3t7UGXIJKympqaoEsQSZlyLC5QjsUVyrK4wI8ca2FERGSIMMYEXYJIypRjcYFyLK5QlsUFfuRYCyOSFoYNGxZ0CSIpi0QiQZcgkjLlWFygHIsrlGVxgR851sKIpIVEIhF0CSIp03ZXcYFyLC5QjsUVyrK4wI8c65/RJS3satjFucvODboM8VF0QTToEo67vLy8oEsQSZlyLC5QjsUVyrK4wI8ca8eIpIUTjKIuQ59uOy0uUI7FBcqxuEJZFhf4kWP9WpS0kGkygy5BBtDixYt56qmnaG9vZ/LkycyZM4c5c+bwxhtvcODAAebNm8fMmTNZtGhR0KWmpKmpKegSRFKmHIsLlGNxhbIsLvAjx1oYkbQQb48HXYIMkM2bN7N//34uvPBCXn/9dS677DLKy8spLy/ntNNOY/Xq1Vx++eWsW7eOxsZGtm3bFnTJx6ykpCToEkRSphyLC5RjcYWyLC7wI8daGHGUMWaJMWbGEbQ73Rhz+hH2ud6PMY92XD/kDdP5ky5KJBIsXLiQk046iSeffJKXX36ZtWvXct5553HzzTfT3t5OJBLhzTffJBaLsXfvXsaOHRt02cesqqoq6BJEUqYciwuUY3GFsiwu8CPHWhiR070/To97iEPHayg5jlatWsXJJ5/MggULqKioIBqN8thjj/HMM8/Q3t7O008/zdlnn83u3bt54IEHmDhxIgUFBUGXfcxCoVDQJYikTDkWFyjH4gplWVzgR451Vxq3nW+M+QcgD/gC8CNgDLAHuAb4AXAJgDHmKmttmTEmG3gYGA1st9bemMKYFwL1wMrDjdtbR8aYJcCngGygBrjCWtvu7Vz5H+Aaa+3HjTEG+Bkw0Wv3JWvt+67A09rQSuTBCI3JRsIZYSaeM5F3TnuHWYWz2NW8i5ZkC6eMOIWN0Y2U5pcSMiE21G+gbFQZOw/uBGBC9gSerXuW6QXTSdgEL8VeYlpkGm81vkVWRhbjw+NZW7uWWYWziLfH2dGwg6kFU9nesJ1IKMLYrLFdx6OJKDubdnLWyLPYFt/GmOFjKB5e3HW8urWafa37mJI3hS0HtjAhZwKRUKTr+N6WvUQTUSbnTmZT/SYm5U4ib1he1/F0mNOePXvYtGkT8+fPp6WlhfPPP5977rmHefPm0dLSwrhx46ioqODxxx9n4cKFjBkzhuXLl3Pfffdx4403UlVVRSgUIj8/n9raWvLz82lra6O5uZmSkhKqqqrIzMwkNzeXuro6CgoKaG5upqWlpet4VlYW4XCY+vp6Ro0aRUNDA21tbV3Hw+EwmZmZxGIxCgsLicViJBKJruM5OTlkZGQQj8cpKioiGo1iraWoqIjq6mpGjBgBQGNjI8XFxTQ3N7Nnzx4ikQg1NTXk5eWRTCZpamrq6nOozammpgZjjOaURnM6ePAg8XjcqTm5+D1pTv3P6eDBg7S2tjo1Jxe/J83p8HOy1lJZWenUnFz8njSn/ud08OBBqqur+/+VehjGWptSBzI4eYsKp1prv2SMuc17O2mtXeodq7LW/psx5moAa+1K73MLgZHW2iXGmEeBJdba17xj6621M45izJ1ABMg/3Lj99Ndmrb3TGHM/sM5a+9/GmLeBn1pr7/XaXQxcbK292hhzD7DeWvt4975WrVll5788/4j+7mRoiC6I8tOf/pTMzEyuu+46Vq9ezRNPPMF3v/tdTj31VC699FIWLVrEihUruPHGGyktLeXrX/8606dP56tf/WrQ5R+TyspKxo0bF3QZIilRjsUFyrG4QlkWF3TmuKKiYmtZWdmZx9KHdoy47WHv8V3gJ8Bc7/XvgYv6+MzJwFTvWiEjgbHAa8c4ZiZwGvDoEYzbl63e42vAeO95DFjWo+ZPeztJRgBv9uyk+VDzUQ4rQ8GXv/xlbr75Zh599FESiQS33347119/PdZaLrroImbMmEFubi433XQTe/bs4cwzz+Syyy4Luuxjlp+fH3QJIilTjsUFyrG4QlkWF/iRYy2MuK37fYv+BjgbeMZ7fN17vxkYBeCdkvI2sMVa+5Ax5vN0LHAc65h44xx2XNv31qWzgLXAFOC33nsHrbXdLxryNrDKWnu7MeazwAf6GmYUdRfl5uaycuXK9733wgsvvO/1GWecwebNm49jVQOnra0t6BJEUqYciwuUY3GFsiwu8CPHuvhq+mgHPmaM2Qh8lI7rfgA8DVxqjHkROAdYDlzktbse2J3iuP9+hOP2pdTbCTISeKKPNo8DY4wxG4A7gMqeDUJGF5aSoa+5WTufZOhTjsUFyrG4QlkWF/iRY11jRAYt7xoj662161Pt68UXX7SnnXZayjWJBKm1tZXhw4cHXYZISpRjcYFyLK5QlsUFnTnWNUbkuPN2cXQXs9Z+YbD011MikfCrK5HAVFVV6QJpMuQpx+IC5VhcoSyLC/zIsRZG5Jj0d3eawdBfTyecoLPGZOjLzMwMugSRlCnH4gLlWFyhLIsL/Mixfi1KWtDCiLggNzc36BJEUqYciwuUY3GFsiwu8CPH+rUoaaG9vT3oEkRSVldXF3QJIilTjsUFyrG4QlkWF/iRYy2MSFoYNkxnjcnQV1BQEHQJIilTjsUFyrG4QlkWF/iRYy2MSFo4dOhQ0CWIpEy31BMXKMfiAuVYXKEsiwv8yLEWRiQtaGFEXNDS0hJ0CSIpU47FBcqxuEJZFhf4kWMtjEhaCIVCQZcgkrKSkpKgSxBJmXIsLlCOxRXKsrjAjxxrYUTSQiKRCLoEkZRVVVUFXYJIypRjcYFyLK5QlsUFfuRYCyOSFnS7XnFBVlZW0CWIpEw5Fhcox+IKZVlc4EeOdasOSQvvxN5h+rLpQZchRyi6IBp0CYNSOBwOugSRlCnH4gLlWFyhLIsL/Mix/hld0kL4BP1HX4a++vr6oEsQSZlyLC5QjsUVyrK4wI8ca2FE0sLB5MGgSxBJ2ahRo4IuQSRlyrG4QDkWVyjL4gI/cjygCyPGmCXGmBm9vH/vEXz2dGPM6QNS2FHW0lu7VOs7XuP29R0cS3+91WyMWX+ktQRp+AnDgy5BjtHixYt56qmnALj55pu54IILuOuuuwCorKzkS1/6Ep/73Oe49dZbgyzzuGhoaAi6BJGUKcfiAuVYXKEsiwv8yHEgO0astQuPoNnp3p/BUEtv7VKqL6hxe3HE/R1pzYNRhskIugQ5Bps3b2b//v1ceOGFlJeXc+jQIX73u9+xa9cu3nnnHZYsWcLixYt58skn2bdvHy+88ELQJQ+otra2oEsQSZlyLC5QjsUVyrK4wI8cH4+Lr55vjPkHIA+40FpbZYxZb62dAWCMCQO/8o7XAZcD/whc4h2/ylpbZowZDqwExgB7gGustW3ejoWXgI9ba2cZY34AvGmtXWWMWQK8BfwV8Lq19jfGmFuAndbaX3n991uLtba9l3Y/7FlfbxM3xnw/oHELvP4yAAOsN8ZkAw8Do4Ht1tobe+vPGDMC+DWQ49V7Tbd+u2rpY9wlwKeAbKAGuAKwwCPAOKAW+CLQDvwnHd/LXqAS+A7wM2Ci99kvAVcBn/D+lADzgDMBrLUrvZ0wnX/2AcVeKVustbd0r62poYnIgxEak42EM8JMPGci75z2DrMKZ7GreRctyRZOGXEKG6MbKc0vJWRCbKjfQNmoMnYe3AnAhOwJPFv3LNMLppOwCV6KvcS0yDTeanyLrIwsxofHs7Z2LbMKZxFvj7OjYQdTC6ayvWE7kVCEsVlju45HE1F2Nu3krJFnsS2+jTHDx1A8vLjreHVrNfta9zElbwpbDmxhQs4EIqFI1/G9LXuJJqJMzp3MpvpNTMqdRN6wvK7jQ31OTU1N1NbWcuONN3LBBRewcuVKtm3bRllZGZWVlXzmM5/ht7/9LW+99RYnn3wylZWV5ObmsnfvXiorKykuLqampgZjDJFIhJqaGvLy8kgmkzQ1NVFSUkJVVRWhUIj8/Hxqa2vJz8+nra2N5ubmruOZmZnk5uZSV1dHQUEBzc3NtLS0dB3PysoiHA5TX1/PqFGjaGhooK2tret4OBwmMzOTWCxGYWEhsViMRCLRdTwnJ4eMjAzi8ThFRUVEo1GstRQVFVFdXc2IESMAaGxspLi4mEOHDrFnzx6n5uTi96Q59T+nZDJJPB53ak4ufk+aU/9zSiaTtLa2OjUnF78nzenwc8rMzKSystKpObn4PWlO/c8pmUxSXV3d18/UI2KstSl10G/nHT+UT7XWfskYcxsdP7T/q8eP/TOA2621c40xc4GN1toDxpiroeMHsNfuJiDfWrvU67fKWvtvxpgW4Epr7aNeu78C/tnrbzMwEzgJ+I619pvGmN8CX7TWNnntD1tLz3be6/fV18f8JwY07neBVmvtvcaYp4GldOwKGWmtXWKMeRRYYq19rZe/54/SsTjxDPAUcIW1trq3WnqZxxKgzVp7pzHmfmAd8DxwPrAaeAj4V+CPwGpr7fnGmApr7SeNMRcDF1trrzbG3AOsByLA14BzgfnAiXQsgPS2MHI18Dvgk0C5tfbc7nWuWrPKzn95fl9/ZTLIRBdEeeSRR3j66af58Y9/zPLly7n33ntZv349kyZNYt26dbz22mu0t7fT0tLCmWeeya233sr69eu7/kPsosrKSsaNGxd0GSIpUY7FBcqxuEJZFhd05riiomJrWVnZmcfSx/E4leZh7/FdILOX4xXADmPM74BZQF9XyTwN+IP3/PfAqd7zHZ2LIgDW2neAXO9H8w5rbbO19n+BE40xecCBzsWJFGo5IkGNC3wYeNV7/rL3eDJwibfD5iPA2D4+m6BjMeLndCxMHO3tXLZ6j68B473+Pk/HDpaPeP0dBIYbY/7gjdNZ36e9+qbxl90fv7DWJug9P121WWt3AfustY107JJ5/6Rs4iinIUHbvn07X/nKVyguLubyyy9n6tSpNDc3A9DU1MShQ4dYvHgx5513Ho888ghXXHGF04sioFvqiRuUY3GBciyuUJbFBUPldr19LQZ0+gTworX2AqAAOMd7v5mOUzIwxhjgdeBs79jZ3muAxl76XAU8yF8WZQC2AAuBx4+hlt70rK8vQYz7LvAx73nn9UPeBu71dnfc6rXprb/r6DiVZj6H/+56c5b3OAXYCVwK7PAe93Zr85i19lPW2ru71bfKq28h8Ib3fs8a2oAi7/lFR1pUe8eZSTKEfPjDH6ayshKAV155hXfffZff//73AOzYsYMPfehDAEyaNIk9e/Zwww03BFbr8ZKZ2dvassjQohyLC5RjcYWyLC7wI8eD4Xa9u4AFxphNdFxHonOHw9PApcaYF+lYKPh34GPGmI3AR+m43khffk3HtS26X4nxV3T84H7iGGrpTc/6+hLEuD8DLvN2X+R57y0HLvL+/q4HdvfR39PALXScBgN97yzpS6k37kg65vwiHdcLeYGOHShj6bjuy7eNMc8ZY/7bGHMOHQtHY4wxG4A76LjuSG/WAXO8U3WO+Iqq4RO0Gj7UfPnLX+b5559n9uzZrFixgvLycn75y1/y/e9/n9/85jdccMEFANx3333ccMMNZGdnB1zxwIvFYkGXIJIy5VhcoByLK5RlcYEfOR7Qa4wEwRjzMTquZfGAtXZF0PWkE+8aI+uttesP02428Ld07P5oBv7LWrtqIGtb8fgK+7VtXxvIIcRH0QXRXt8/cOAAzz33HFOnTqW4uLjXNi5ramoiJycn6DJEUqIciwuUY3GFsiwu6MxxKtcYOR53pTmurLWv85fTOY4bb5dEdzFr7RdcHbc31tolR9huDbBmYKt5vwn5E/r8sS1Dx8iRI7nkkkuCLiMwsVhM//MiQ55yLC5QjsUVyrK4wI8cO7cwEpT+bmPr4rhDjWs7oyQ9JRK6iLAMfcqxuEA5Flcoy+ICP3I8GK4xIjLgQqFQ0CWIpKykpCToEkRSphyLC5RjcYWyLC7wI8daGJG0oNVwcUFVVVXQJYikTDkWFyjH4gplWVzgR461MCJpISPjiG9gIzJo6RxgcYFyLC5QjsUVyrK4wI8ca2FERGSI0AKfuEA5Fhcox+IKZVlc4EeOtTAiaSGZTAZdgkjK4vF40CWIpEw5Fhcox+IKZVlc4EeOtTAiaUEXXxUXFBUVBV2CSMqUY3GBciyuUJbFBX7kWAsjkhba29uDLkEkZdFoNOgSRFKmHIsLlGNxhbIsLvAjx1oYEREZIqy1QZcgkjLlWFygHIsrlGVxgR851sKIpIVhw4YFXYJIyrTdVVygHIsLlGNxhbIsLvAjx/q1KGlh94HdfHbZZ4MuIzDRBdom6YLq6mrGjRsXdBkiKVGOxQXKsbhCWRYX+JFj7RiRtNB6qDXoEgaF+vp6nnvuOerq6lJqI8EYMWJE0CWIpEw5Fhcox+IKZVlc4EeOtTAivjLGLDHGzDiCdqcbY04/wj7Xp1qXwIEDB7jiiiuoqKhg7ty51NbWArB48WKeeuqpftuIiIiIiIi4SqfSSFA6F0VeOR6DDT9h+PEYZlB7/fXXueOOOygtLeXAgQO8+uqrZGdns3//fi688MI+25SVlQVcuXRqbGxk1KhRQZchkhLlWFygHIsrlGVxgR851o4RGQjnG2M2GmNeMcaMM8b8whizwRjzc2NMpjHmh8D3gO8ZY54FMMZkG2N+7X3u/r46NsZkGWNWGWNeMMY8YYzJ9t5fb4z5sTFmbW+fa0g2DMQ8h5TPfOYzlJaWsmnTJioqKigtLWXhwoWcdNJJPPnkk322kcGjuLg46BJEUqYciwuUY3GFsiwu8CPH2jEiA2GCtXaaMeY24KvADmvtfGPMEuBaa+0txpi3Aay1K73PfMNrt8QY86gx5uPW2td66fsbwKvW2iuMMdcAk4AtwNnAMmvt3/RWUFZzFpEHIzQmGwlnhJl4zkTeOe0dZhXOYlfzLlqSLZwy4hQ2RjdSml9KyITYUL+BslFl7Dy4s2NS2RN4tu5ZphdMJ2ETvBR7iWmRabzV+BZZGVmMD49nbe1aZhXOIt4eZ0fDDqYWTGV7w3YioQhjs8Z2HY8mouxs2slZI89iW3wbY4aPoXh4cdfx6tZq9rXuY0reFLYc2MKEnAlEQpGu43tb9hJNRJmcO5lN9ZuYlDuJvGF5Xcd7zmnPnj1YayksLOThhx8mOzubhx56iJNOOolvfvOb/Ou//is7duzgpptuYv/+/axatYrs7Gzee+89hg8fTlVVFaFQiPz8fGpra8nPz6etrY3m5mZKSkqoqqoiMzOT3Nxc6urqKCgooLm5mZaWlq7jWVlZhMNh6uvrGTVqFA0NDbS1tXUdD4fDZGZmEovFKCwsJBaLkUgkuo7n5OSQkZFBPB6nqKiIaDSKtZaioiKqq6u7zi1sbGykuLiYmpoajDFEIhFqamrIy8sjmUzS1NTU1edQm9POnTsZOXKkU3Ny8XvSnPqf05///GfGjRvn1Jxc/J40p/7nVFdXx8SJE52ak4vfk+Z0+DlVV1cTDoedmpOL35Pm1P+c/vjHPzJ69Oh+f6AejtG9q8VP3uLHS9baNcaYq4GfAHOttc8YYy4ELrLWfss71rUwYoz5KTAVqAdGArdYa3/rHVtvrZ3hPf8J8N/W2meNMcbrwxpjXrbWntlXXb9Y8wt75ctXDsSUh4Sed6VZunQpjz/+OEuXLuW8887j7bffZunSpTz88MPva3Pqqady6aWXHu9ypQ979uzhxBNPDLoMkZQox+IC5VhcoSyLCzpzXFFRsbWsrKzP34T90ak0MhCauj3/Gzp2c+A9vu49bwY6T4MxwNvAvd4CyK3Au330/RbQeX7H3wFf85439ltQsqm/w2nhX/7lX1i1ahUA8XicK6+8ksrKSgBeeeUVTjzxxA+0yc/PD6xe+aBIJBJ0CSIpU47FBcqxuEJZFhf4kWMtjMhAawc+ZozZCHwUWOm9/zRwqTHmReAcYDlwkdfuemB3H/0tBz7p3anmk8AjR1LEiAzdiuyrX/0qq1evZvbs2SSTSa699lqef/55Zs+ezYoVK7jppps+0GbmzJlBly3d1NTUBF2CSMqUY3GBciyuUJbFBX7kWKfSSFpYWb7SXlNxTdBlBKbnqTQyNNXX11NQUBB0GSIpUY7FBcqxuEJZFhd05lin0ogcxglGUZehL5lMBl2CSMqUY3GBciyuUJbFBX7kWHelkbTwoREf0q4JGfKampooLCwMugyRlCjH4gLlWFyhLIsL/Mix/hld0kIoFAq6BJGUlZSUBF2CSMqUY3GBciyuUJbFBX7kWAsjkhYSiUTQJYikrKqqKugSRFKmHIsLlGNxhbIsLvAjx1oYkbTQcUdgkaFNO5/EBcqxuEA5Flcoy+ICP3KshRFJCxkZGUGXIJKy/Pz8oEsQSZlyLC5QjsUVyrK4wI8ca2FE0kJ7e3vQJYikrLa2NugSRFKmHIsLlGNxhbIsLvAjx1oYkbSgHSPiAv2rjrhAORYXKMfiCmVZXKAdIyJHyFobdAkiKWtrawu6BJGUKcfiAuVYXKEsiwv8yLEWRiQtHDp0KOgSRFLW3NwcdAkiKVOOxQXKsbhCWRYX+JFjLYxIWtAVt8UFftyjXSRoyrG4QDkWVyjL4gI/cjzMhzpEBr3dB3bz2WWfDbqMYxJdEA26BBkkqqqqGDduXNBliKREORYXKMfiCmVZXOBHjrVjRNJC0iaDLkEkZZmZmUGXIJIy5VhcoByLK5RlcYEfOdbCiKSF1kOtQZdwzOLxOJdffjmXXnopV111VdfFhRYvXsxTTz31vrb79+9n+vTpQZQpx0Fubm7QJYikTDkWFyjH4gplWVzgR461MCKBMcas7+fYEmPMDD/6AsjOyD7iugabX/3qV9xwww08+uijjB49mmeffZbNmzezf/9+Lrzwwve1ve2222hpaQmoUhlodXV1QZcgkjLlWFygHIsrlGVxgR851sKIpIXmQ0P3itvXXXcd5557LgC1tbWMHDmShQsXctJJJ/Hkk092tdu4cSPZ2dmMHj06qFJlgBUUFARdgkjKlGNxgXIsrlCWxQV+5FgLIxI4Y8wIY8xTxpjnjTEPdTv0bWPMBmPMKmNMhumw3Hvv18aYjCMdI2SG/l1ptmzZQiwWY+fOnZx88sksWLCAiooKfvazn9HW1sZdd93F7bffHnSZMoB0Sz1xgXIsLlCOxRXKsrjAjxzrrjQyGPwf4D7gGeApY0yx9/7L1tp/MMY8AMzx3gtZa6cbY+4BZgOPH9EIByHyYITGZCPhjDATz5nIO6e9w6zCWexq3kVLsoVTRpzCxuhGSvNLCZkQG+o3UDaqjJ0HdwIwIXsCz9Y9y/SC6SRsgpdiLzEtMo23Gt8iKyOL8eHxrK1dy6zCWcTb4+xo2MHUgqlsb9hOJBRhbNbYruPRRJSdTTs5a+RZbItvY8zwMRQPL+46Xt1azb7WfUzJm0JjYyO7d+9m0aJF/Md//Ad33303X/jCFxg+fDif+cxnWL58Obt372bu3LlkZWXR0tJCbW0tGRkZxONxioqKiEajWGspKiqiurqaESNGANDY2EhxcTE1NTUYY4hEItTU1JCXl0cymaSpqYmSkhKqqqoIhULk5+dTW1tLfn4+bW1tNDc3dx3PzMwkNzeXuro6CgoKaG5upqWlpet4VlYW4XCY+vp6Ro0aRUNDA21tbV3Hw+EwmZmZxGIxCgsLicViJBKJruM5OTlpP6f9+/eTSCScmpOL35Pm1P+cqqurCYfDTs3Jxe9Jc+p/Tp07OF2ak4vfk+Z0+DlFo9H31eTCnFz8njSn/udUXV19RD8J+2OstSl3InIsjDHrrbUzjDHjgX8GksBHgS8AVwObrbVrjTHfBEbQsZB3LfCe9/oBa+3y7n31NdbP/udn9puvfHPgJjOAqq6vYt68eXzrW9/i3HPP5ac//SmZmZlcd911rF69mldffZVXX32VE07o2AC2fft25s6dy7JlywKuXPzW2trK8OHDgy5DJCXKsbhAORZXKMvigs4cV1RUbC0rKzvzWPrQqTQyGFwH/BqYDzR1e/8M7/HjwC7gbWCVtwCyEHjjSAfIG5bnR52B+M///E9effVV7rnnHubMmcPIkSN5/vnnmT17NitWrOCmm25izZo1lJeXU15ezuTJk7Uo4qiqqqqgSxBJmXIsLlCOxRXKsrjAjxzrVBoZDJ4GfgJc770e6z2eY4zZANQA/wMcAmZ771ngy0c6QLtt96/a4+zaa6/l2muvfd978+fP77N9eXn5QJckAcnKygq6BJGUKcfiAuVYXKEsiwv8yLEWRiQwnae+WGs3ApN6HH6xj499vb+++pKwiaOsTmTwCYfDQZcgkjLlWFygHIsrlGVxgR851sKIpIUP536Y6IJo0GWIpKS+vh2aSjIAAA1rSURBVJ68vKF7WpgIKMfiBuVYXKEsiwv8yLGuMSJpYdgwrQHK0Ddq1KigSxBJmXIsLlCOxRXKsrjAjxxrYUTSwqFDh4IuQSRlDQ0NQZcgkjLlWFygHIsrlGVxgR851sKIpAUtjIgL2tragi5BJGXKsbhAORZXKMviAj9yrIURSQuhUCjoEkRSVlJSEnQJIilTjsUFyrG4QlkWF/iRYy2MSFpIJHRXGhn6/LhHu0jQlGNxgXIsrlCWxQV+5FgLI5IWTjhBUZehT7fUExcox+IC5VhcoSyLC/zIsX4tSlowxgRdgkjKMjMzgy5BJGXKsbhAORZXKMviAj9yrIURSQvJZDLoEkRSFovFgi5BJGXKsbhAORZXKMviAj9yrIURSQvDhg0LugSRlBUWFgZdgkjKlGNxgXIsrlCWxQV+5FgLI5IWtGNEXKB/1REXKMfiAuVYXKEsiwv8yLH+GV3SwnuN7zFj2Ywjbh9dEB24YkSOke6uJC5QjsUFyrG4QlkWF/iRY+0YkbQQb48HXYJIyvy4R7tI0JRjcYFyLK5QlsUFfuRYCyOSFvKG5R3T5xYvXsxTTz3FgQMHmDdvHjNnzmTRokU+VydyZPy4R7tI0JRjcYFyLK5QlsUFfuRYCyOSFtps21F/ZvPmzezfv58LL7yQ1atXc/nll7Nu3ToaGxvZtm3bAFQp0r+cnJygSxBJmXIsLlCOxRXKsrjAjxxrYUQGPWPM+lT7OGQPHVX7RCLBwoULOemkk3jyySeJRCK8+eabxGIx9u7dy9ixY1MtSeSoZWRkBF2CSMqUY3GBciyuUJbFBX7kWAsjkhayTsg6qvarVq3i5JNPZsGCBVRUVPCnP/2J3bt388ADDzBx4kQKCgoGqFKRvsXjulaODH3KsbhAORZXKMviAj9yrLvSiK+MMVnASuBE4AAwz1p7sEeb7wOvW2t/Y4y5BdgJ/Bb4NZAD7LTWXtNH/0uA9dba9caYq723fwk8DIwGtltrb+z5uYMNB4k8GKEx2Ug4I8zEcybyzmnvMKtwFruad9GSbOGUEaewMbqR0vxSNm3YxPz582lpaeH888/nBz/4AT/+8Y/5q7/6K+6++27uv/9+vvGNb1BTU0NeXh7JZJKmpiZKSkqoqqoiFAqRn59PbW0t+fn5tLW10dzc3HU8MzOT3Nxc6urqKCgooLm5mZaWlq7jWVlZhMNh6uvrGTVqFA0NDbS1tXUdD4fDZGZmEovFKCwsJBaLkUgkuo7n5OSQkZFBPB6nqKiIaDSKtZaioiKqq6sZMWIEAI2NjRQXF1NTU4MxhkgkojkN4jklk0n27Nnj1Jxc/J40p/7nlEgkiMfjTs3Jxe9Jczr8nFpbW52bk4vfk+bU/5yGDRtGZWWlU3Ny8XvSnPqfUyKRoLq6urefj0fMWGtT6kCkO2PMAiDHWvtDY8w1dCyAbOnRZiLwHWvtN40xvwW+CIwBJgLPAE8BV1hrq7326621M7znS/jgwshIYKS1dokx5lFgibX2te5j/mLNL+yVL195xPNYGlpKZmYm1113HatXr+aJJ57gxhtvpLS0lK9//etMnz6dr371q0f5tyOSmj179nDiiScGXYZISpRjcYFyLK5QlsUFnTmuqKjYWlZWduax9KFTacRvpwCdCyErgZd6NrDW/i9wojEmDzhgrW0CEsDXgJ8DESB8BGN1tjkZuMS7FslHgA9cAMRgjmoSX/7yl3n++eeZPXs2K1as4Prrr2fRokWMHz+e+vp6LrvssqPqT8QPWsgWFyjH4gLlWFyhLIsL/MixTqURv70FlALPAn8H7AeW99JuC7AQeNx7fR0dp9L8EtjQT/9tQJH3/ELgMeBtYIu19iFjzOeBd3t+qCHZcFSTyM3NZeXKle97b/PmzUfVh4jfioqKDt9IZJBTjsUFyrG4QlkWF/iRY+0YEb8tBz7p7d74JPBIH+1+RcfCyBPe66eBW4B13uu+bvvyOHCzMebfgLpuY15kjNkIXA/s7vmh3Izco5uFyCCU6rmTIoOBciwuUI7FFcqyuMCPHGvHiPjKWtsMzDuCdm/QccpM5+uNwKQ+2s7o9nwHMK2XZv2OOTZvLNEF0cOVJTKodV7ISmQoU47FBcqxuEJZFhf4kWMtjMiA8naOdBez1n4hiFpEREREREREetKpNDKgrLUzevwJZFEkmUwGMayIrxobG4MuQSRlyrG4QDkWVyjL4gI/cqyFEUkLoVAo6BJEUlZcXBx0CSIpU47FBcqxuEJZlv/f3v2FWlaXYRz/Ps2MgynTeFAcvEhIvCjSMUPRCJucPyVoVFCGWdFMXVlQXdTYFEQhCVkEhRdTWhEUKExTxIga5h+oICM0b0KKNMQBh2k0B5Q59naxl7DJM3ps7+2a9VvfD2xY6z17r/MueNis857fXrsF88ixgxGNwvLyct8tSDN76qmn+m5Bmpk5VgvMsVphltWCeeTYwYgkDUSSvluQZmaO1QJzrFaYZbVgHjl2MKJRWLvW+wxr+JaWll75SdIJzhyrBeZYrTDLasE8cuxgRKNw7NixvluQZuZyV7XAHKsF5litMMtqgR+lkVZpzZo1fbcgzWzDhg19tyDNzByrBeZYrTDLasE8cuxgRJIGwq+dVgvMsVpgjtUKs6wWzCPHDkY0Cr7pqwVHjx7tuwVpZuZYLTDHaoVZVgvmkWMHIxqFdevW9d2CNLNNmzb13YI0M3OsFphjtcIsqwXzyLGDEY2CN19VCw4ePNh3C9LMzLFaYI7VCrOsFswjxw5GNApHjhzpuwVpZvv37++7BWlm5lgtMMdqhVlWC+aRYwcjGgUHI2rBvn37+m5Bmpk5VgvMsVphltWCeeTYwYhGoar6bkGa2fLyct8tSDMzx2qBOVYrzLJaMI8cxz8YNQYHDhz49/r16//adx/SLA4fPnz60tLSob77kGZhjtUCc6xWmGW1YCrHZ2/duvWM/+cYDkYkSZIkSdJo+VEaSZIkSZI0Wg5GJEmSJEnSaDkYkSRJkqYkWUqyPcnpffciSVo8ByNqXpJbkvw+yVf67kV6OUnOTPLA1P5LsrvamtSHJG9IckeSu5L8IslJ5lhDk+Q04NfAxcBvk5xhjjVU3bXFn7ttc6xBSbI2yeNJ7u0e5y0qxw5G1LQkHwTWVNWlwJuSnNt3T9JKugvxnwCndPsvye5qa32dgwR8FPhOVe0ADgIfwRxreM4HvlBVNwB3ApdjjjVcNwEne12hgTof+HlVbamqLcC5LCjHaxd4EtKJYAtwW7d9F/BO4NHeupGO7wXgauCX3f4WXprdt62yZsbVi6q6eWr3DOBa4LvdvjnWIFTVfQBJLmOyamQJ3481QEkuB44yGVRvwRxreC4BrkzybuAvwPMsKMeuGFHrTgGe6LYPA2f22It0XFX1TFU9PVVaKburrUm9SnIpcBrwT8yxBihJmAyr/wUU5lgDk+Qk4KvA7q7kdYWG6I/Atqq6GFgHXMGCcuxgRK17Fji52z4VM6/hWCm7q61JvUmyBHwP2Ik51kDVxHXAw8A7MMcant3AzVV1pNv3/VhD9HBVPdltPwiczoJybNDVuj8xWToFsBn4R3+tSK/KStldbU3qRfcfytuB66vqMcyxBijJl5J8vNvdCNyIOdbwbAOuS3IvcAFwFeZYw/PTJJuTrAHeD1zHgnLsPUbUuv3AA0nOYrL06pKe+5FWa6Xs1iprUl92ARcCe5LsAX4EfMwca2D2Arcl+RTwCJP34/vNsYakqi57cbsbjrwPrys0PF8HfgYE+BULvD5OVS3kDKQTRfdtH9uB+6vqYN/9SKu1UnZXW5NOFOZYLTDHaoE5VgsWlWMHI5IkSZIkabS8x4gkSZIkSRotByOSJEmSJGm0HIxIkiT1KMnXkjyb5ODU4+q++5IkaSz8VhpJkqT+fb+qdvfdhCRJY+SKEUmSJEmSNFoORiRJkgYkyeuS7E3yZJLHk3xgqn5TkieSPJpkx1T92139oSQXTR2rklyY5MEk35iqf7k79mNJrnrtz1KSpNeOgxFJkqT+fWbq/iKffoXnXgBcCZwNvAfY3tV3AZuBc4BPAD/u6ju715wDfB64Pcn6qeN9q3vtNwGSXAFsBd4M7AD2Jlk309lJknQC8x4jkiRJ/Xs19xj5G/AfJgONe4DPdfX3Aj+squeA3wFndfUrgB909XuSPA2cBzzY/XxPVT00dfxtwEXd7wF4fXesx171WUmSNACuGJEkSRqQqnoaeAvwAHANcPdKz0vyySSnvviy6UNM71fVH/73pcANVbWpqjYBbwSemFP7kiSdcByMSJIkDUiSrcCtwH7geuDiJAHuBHYmWZ/krcCNwHPAHcCurv4uYCPwyMv8it8AH06yIclZTFaObFzcGUmS1C8/SiNJkjQs9wHXMlnFsQx8saoqyS1M7gvyd+AZ4JqqWk5y61T9EPChqnr+eAevqgNJ3s5kePIC8NmqOrTQM5IkqUepqld+liRJkiRJUoP8KI0kSZIkSRotByOSJEmSJGm0HIxIkiRJkqTRcjAiSZIkSZJGy8GIJEmSJEkaLQcjkiRJkiRptByMSJIkSZKk0XIwIkmSJEmSRuu/cFot8SRj1JsAAAAASUVORK5CYII=的分析出的重要特征图.jpg', dpi=400, bbox_inches='tight')
plt.show()

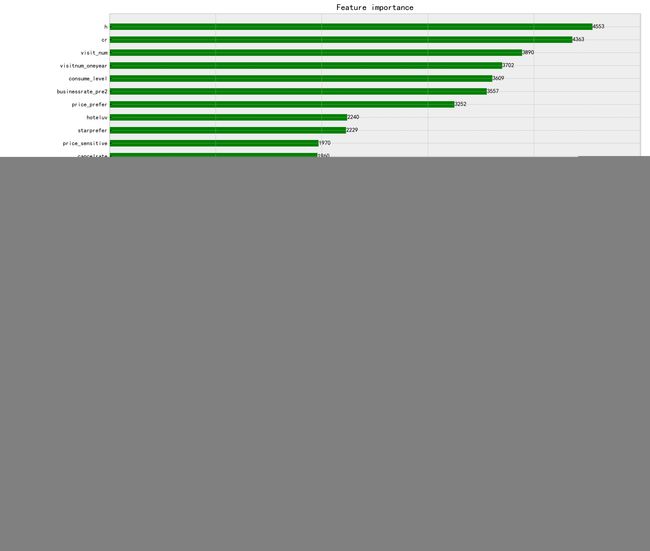
看出重要特征超过2000以上的有：h, cr, visit_num, visit_oneyear, consume_level, price_prefer, businessrate_pre2, hoteluv, starprefer，后面分析时也会重点查看这些特征的影响

6.2.2 K-means聚类

K-Means算法是一种基于划分的无监督聚类算法，它以 k 为参数，把 n 个数据对象分成 k 个簇，使簇内具有较高的相似度，而簇间的相似度较低。

由上文的特征相关性分析，我们对相关性高的特征进行降维

visit_num=['decisionhabit_user','historyvisit_avghotelnum']        #用户访问数
pca=PCA(n_components=1)
rawdf['visit_num']=pca.fit_transform(rawdf[visit_num])
rawdf.drop(visit_num,axis=1,inplace=True)

# 选取出几个刻画用户的重要指标
user_feature = ['ordercanncelednum','ordercanceledprecent','consume_level','starprefer','lasthtlordergap','lastpvgap','h','sid',
                'c_value','landhalfhours','price_sensitive','price_prefer','day_advanced','ordernum_1_year','visit_num']
user_attributes = rawdf[user_feature]
# user_attributes.head(30).T

# 数据标准化
from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
scaler.fit(user_attributes)
user_attributes = scaler.transform(user_attributes)

# 对选出的关键特征k-means聚类，来做用户画像
from sklearn.cluster import KMeans
Kmeans = KMeans(n_clusters=3)  
Kmeans.fit(user_attributes)
k_char = Kmeans.cluster_centers_  # 得到每个分类的质心

persons = pd.DataFrame(k_char.T, index=user_feature,  columns=['0类','1类','2类'] )

plt.figure(figsize=(6,12))
sns.heatmap(persons, xticklabels=True, yticklabels=True, square=False, linewidths=.5, annot=True, cmap='Oranges')
plt.savefig('./images/用户画像表.jpg',dpi=400, bbox_inches='tight')
plt.show()

从热力图可以看出：

• 1类用户消费水平（consume_level）和价格偏好（price_prefer）为三类用户中最高，同时较高的星级偏好反应出该类型用户对酒店有一定的质量要求，但同时该类型用户对价格的敏感度(price_sensitive)最高，最近一年下单频率是三类用户中最低的，上次消费时间间隔很久，他们一般会提前较早的时间预定酒店，并且订单取消率是三类用户中最低的，因此可以推测该类型用户为旅游客户，结合sid来看他们是高价值客户。

• 2类用户最近一年下单频率（ordernum_1_year）为三类用户中最高，但同时该类型用户的订单取消率也是最高的。他们的消费水平一般，对酒店的偏好也一般，但对价格敏感度不高，一般不会提前预定酒店。他们使用携程浏览酒店的次数较高，基本是老用户，并且用户价值是三类用户中中等的，因此将2类用户定义为中等价值客户。

• 0类用户的可视化数据基本是白色的，客户消费水平和使用频率都是最低的，因此将这类用户归为“低价值用户”，但sid反映出他们大部分是新客户。

对三种客户占比进行可视化

plt.figure(figsize=(9,9))

class_k=list(Kmeans.labels_)                          # 每个类别的用户个数
percent=[class_k.count(0)/len(user_attributes),
         class_k.count(1)/len(user_attributes),
         class_k.count(2)/len(user_attributes)]       # 每个类别用户个数占比

fig, ax = plt.subplots(figsize=(10,10))
colors=['peachpuff','sandybrown','chocolate']
types=['低价值客户','高价值用户','中等价值用户']


ax.pie(percent,radius=1,autopct='%.2f%%',pctdistance=0.75,colors=colors,labels=types)
ax.pie([1], radius=0.6,colors='w')
plt.savefig('./images/用户画像占比.jpg',dpi=400, bbox_inches='tight')
plt.show()

从饼图看出，高价值用户占比13.26%；中等价值用户占比偏低，仅有6.19%，需要扩大中等价值用户群体，同时，低价值用户占比高达80.55%，其中很多是新用户，需要把这些新用户转化。

6.2.3 用户画像分析

高价值用户分析

高价值用户特点：消费水平高、客户价值较大、追求高品质的酒店（有星级偏好）,老客户居多，他们对酒店价格很敏感，一般会提前较早的时间预定酒店，订单取消率是三类用户中最低的，但最近一年下单频率也是最低的，上次消费时间间隔很久。因此可以合理推断，这类用户预定酒店的目的可能多为出门旅行。

针对这部分客户，我们需要：

1. 在节假日前两三周定期尽可能推送较多的酒店，因为此类用户通常比较喜欢浏览、综合考虑
2. 推荐的酒店品质可以高一些，同时价格要具有吸引力。再推荐当地旅游资讯，吸引用户关注，因为这类用户旅游出行的概率较大，然后通过用户的点击行为优化酒店推荐的准确度（在价格、星级、地点、类别方面）
3. 和景区酒店代理商合作，针对此类用户定制个性化推荐，多推荐性价比高的酒店

中等价值分析

中等价值客户特点：消费水平一般，对酒店的偏好也一般，基本是老客户，用户价值大，同时对价格敏感度不高。他们经常浏览酒店信息，24小时登录时长较长，因此可能再对比价格选择酒店。他们经常下单预定酒店，但一般不会提前，同时订单取消率也很高。可以合理推测改类型用户的商务属性比较重，他们可能需要经常出差，一般不会提前太久预定酒店，出差行程可能有变动因此可能取消订单。

这部分客户仅占6.19%，因此针对这部分客户，我们需要：

1. 多推荐价格实惠的商务酒店来吸引用户，并结合用户画像进行建模优化的推荐；
2. 定期推送平台信息，持续维护用户；

低价值客户分析

低价值客户特点：最明显的特征就是浏览次数和浏览时长都很低，消费水平、用户价值都是最低的，浏览次数和订单都很低，这部分用户可能偶尔才在携程上预定酒店，几乎没有消费过，对酒店品质几乎不追求，因此重点在于激活用户。同时，由于sid值很低，说明大部分是新客户刚注册或者注册后就不使用了的。

由于低价值客户占比高达80%，因此需要促进改用户群体的转化：

• 对于长久未登录的用户，可以通过信息推送来提醒、挽回用户，并发放优惠券来刺激消费；
• 由于新用户，他们属于潜在客户，因此建议把握用户初期体验（如初期消费折扣活动、打卡活动等），还可以定期推送实惠的酒店给此类用户，以培养用户的消费习惯为主。
• 推送的内容也要引导用户转化，推荐的内容可以多为大减价、大酬宾、跳楼价之类的；
• 初期用户画像数据较少的时候，酒店推荐可以结合当季热门酒店、热门资讯、附近的人较多选择的酒店等，然后逐渐完善用户画像。