面板模型混合效应模型
This article shows how tree-boosting (sometimes also referred to as “gradient tree-boosting”) can be combined with mixed effects models using the GPBoost algorithm. Background is provided on both the methodology as well as on how to apply the GPBoost library using Python. We show how (i) models are trained, (ii) parameters tuned, (iii) model are interpreted, and (iv) predictions are made. Further, we do a comparison of several alternative approaches.
本文展示了如何使用GPBoost算法将树增强(有时也称为“梯度树增强”)与混合效果模型结合使用。 提供了方法论以及如何使用Python应用GPBoost库的背景知识 。 我们展示了如何(i)训练模型,(ii)调整参数,(iii)解释模型,以及(iv)进行预测。 此外,我们对几种替代方法进行了比较。
介绍 (Introduction)
Tree-boosting with its well-known implementations such as XGBoost, LightGBM, and CatBoost, is widely used in applied data science. Besides state-of-the-art predictive accuracy, tree-boosting has the following advantages:
借助XGBoost,LightGBM和CatBoost等著名的实现来增强树性能在应用数据科学中得到了广泛的应用。 除具有最新的预测准确性外,增强树功能还具有以下优点:
- Automatic modeling of non-linearities, discontinuities, and complex high-order interactions 自动建模非线性,不连续和复杂的高阶相互作用
- Robust to outliers in and multicollinearity among predictor variables 稳健的预测变量中的异常值和多重共线性
- Scale-invariance to monotone transformations of the predictor variables 尺度不变性到预测变量的单调变换
- Automatic handling of missing values in predictor variables 自动处理预测变量中的缺失值
Mixed effects models are a modeling approach for clustered, grouped, longitudinal, or panel data. Among other things, they have the advantage that they allow for more efficient learning of the chosen model for the regression function (e.g. a linear model or a tree ensemble).
混合效果模型是针对聚类,分组,纵向或面板数据的建模方法。 除其他优点外,它们还具有以下优点:允许更有效地学习所选的回归函数模型(例如线性模型或树集合)。
As outlined in Sigrist (2020), combined gradient tree-boosting and mixed effects models often performs better than (i) plain vanilla gradient boosting, (ii) standard linear mixed effects models, and (iii) alternative approaches for combing machine learning or statistical models with mixed effects models.
如Sigrist(2020)所述, 结合梯度树增强和混合效应模型的性能通常比(i)普通香草梯度增强,(ii)标准线性混合效应模型和(iii)结合机器学习或统计的替代方法要好。具有混合效果模型的模型。
建模分组数据 (Modeling grouped data)
Grouped data (aka clustered data, longitudinal data, panel data) occurs naturally in many applications when there are multiple measurements for different units of a variable of interest. Examples include:
当对感兴趣变量的不同单位进行多次测量时,在许多应用程序中自然会出现分组数据(又名聚类数据,纵向数据,面板数据) 。 示例包括:
- One wants to investigate the impact of some factors (e.g. learning technique, nutrition, sleep, etc.) on students’ test scores and every student does several tests. In this case, the units, i.e. the grouping variable, are the students and the variable of interest is the test score. 一个人想调查某些因素(例如学习技术,营养,睡眠等)对学生考试成绩的影响,而每个学生都进行几次考试。 在这种情况下,单位,即分组变量,是学生,而感兴趣的变量是测试分数。
- A company gathers transaction data about its customers. For every customer, there are several transactions. The units are then the customers and the variable of interest can be any attribute of the transactions such as prices. 公司收集有关其客户的交易数据。 对于每个客户,都有几笔交易。 单位就是客户,兴趣变量可以是交易的任何属性,例如价格。
Basically, such grouped data can be modeled using four different approaches:
基本上,可以使用四种不同的方法对此类分组数据进行建模:
Ignore the grouping structure. This is rarely a good idea since important information is neglected.
忽略分组结构 。 因为忽略了重要信息,所以这很少是一个好主意。
Model each group (i.e. each student or each customer) separately. This is also rarely a good idea as the number of measurements per group is often small relative to the number of different groups.
分别对每个小组(即每个学生或每个客户)建模 。 这也不是一个好主意,因为每组的测量数量相对于不同组的数量通常很小。
Include the grouping variable (e.g. student or customer ID) in your model of choice and treat it as a categorical variable. While this is a viable approach, it has the following disadvantages. Often, the number of measurements per group (e.g. number of tests per student, number of transactions per customer) is relatively small and the number of different groups is large (e.g. number of students, customers, etc.). In this case, the model needs to learn many parameters (one for every group) based on relatively little data which can make the learning inefficient. Further, for trees, high cardinality categorical variables can be problematic.
在您选择的模型中包括分组变量(例如,学生或客户ID),并将其视为分类变量。 尽管这是一种可行的方法,但它具有以下缺点。 通常,每组的测量数量(例如,每个学生的测试数量,每个客户的交易数量)相对较小,而不同组的数量却很大(例如,学生,客户数量等)。 在这种情况下,模型需要基于相对较少的数据来学习许多参数(每组一个),这会使学习效率低下。 此外,对于树木,高基数类别变量可能会出现问题。
Model the grouping variable using so-called random effects in a mixed effects model. This is often a sensible compromise between the approaches 2. and 3. above. In particular, as illustrated below and in Sigrist (2020), this is beneficial compared to the other approaches in the case of tree-boosting.
在混合效应模型中使用所谓的随机效应对分组变量进行建模。 这通常是上述方法2和方法3之间的明智折衷。 尤其是,如下面和Sigrist(2020)中所示,与在树增强情况下的其他方法相比,这是有益的。
方法论背景 (Methodological background)
For the GPBoost algorithm, it is assumed that the response variable y is the sum of a non-linear mean function F(X) and so-called random effects Zb:
对于GPBoost算法,假定响应变量y是非线性均值函数F(X)与所谓的随机效应Zb的和 :
y = F(X) + Zb + e
y = F(X)+ Zb + e
where
哪里
- y the response variable (aka label) y响应变量(也称为标签)
- X contains the predictor variables (aka features) and F() is a potentially non-linear function. In linear mixed effects models, this is simply a linear function. In the GPBoost algorithm, this is an ensemble of trees. X包含预测变量(又称特征),F()是潜在的非线性函数。 在线性混合效果模型中,这只是线性函数。 在GPBoost算法中,这是一棵树木。
- Zb are the random effects which are assumed to follow a multivariate normal distribution Zb是假定遵循多元正态分布的随机效应
- e is an error term e是错误项
The model is trained using the GPBoost algorithm, where trainings means learning the (co-)variance parameters (aka hyper-parameters) of the random effects and the regression function F(X) using a tree ensemble. The random effects Zb can be estimated (or predicted, as it is often called) after the model has been learned. In brief, the GPBoost algorithm is a boosting algorithm that iteratively learns the (co-)variance parameters and adds a tree to the ensemble of trees using a gradient and/or a Newton boosting step. The main difference to existing boosting algorithms is that, first, it accounts for dependency among the data due to clustering and, second, it learns the (co-)variance of the random effects. See Sigrist (2020) for more details on the methodology. In the GPBoost library, (co-)variance parameters can be learned using (accelerated) gradient descent or Fisher scoring, and trees are learned using the LightGBM library. In particular, this means that the full functionality of LightGBM is available.
使用GPBoost算法对模型进行训练,其中训练意味着 使用树集合 学习 随机效应 的(共)方差参数(aka超参数) 和回归函数F(X) 。 在学习模型之后,可以估计(或预测,通常称为)随机效应Zb。 简而言之,GPBoost算法是一种增强算法,它迭代地学习(协)方差参数,并使用梯度和/或牛顿增强步骤将一棵树添加到树的集合中。 与现有增强算法的主要区别在于,首先,它考虑了由于聚类导致的数据之间的依赖性,其次,它学习了随机效应的(协)方差。 有关该方法的更多详细信息,请参见Sigrist(2020) 。 在GPBoost库中,可以使用(加速)梯度下降或Fisher评分来学习(协)方差参数,而可以使用LightGBM库来学习树。 特别是,这意味着可以使用LightGBM的全部功能。
如何在Python中使用GPBoost库 (How to use the GPBoost library in Python)
In the following, we show how combined tree-boosting and mixed effects models can be applied using the GPBoost library from Python. Note that there is also an equivalent R package. More information on this can be found here.
在下面的内容中,我们展示了如何使用Python的GPBoost库应用组合的树加速和混合效果模型。 请注意,还有一个等效的R包。 有关此的更多信息,请参见此处 。
安装 (Installation)
pip install gpboost -U模拟数据 (Simulate data)
We use simulated data here. We adopt a well known non-linear function F(X). For simplicity, we use one grouping variable. But one could equally well use several random effects including hierarchically nested ones, crossed ones, or random slopes. The number of samples is 5'000 and the number of different groups or clusters is 500. We also generate test data for evaluating the predictive accuracy. For the test data, we include both known, observed groups as well as novel, unobserved groups.
我们在这里使用模拟数据。 我们采用了众所周知的非线性函数F(X) 。 为简单起见,我们使用一个分组变量。 但是同样可以很好地使用几种随机效果,包括层次嵌套的效果,交叉效果或随机斜率。 样本数量为5,000,不同组或群集的数量为500。我们还生成测试数据以评估预测准确性。 对于测试数据,我们既包括已知的观察组,也包括新颖的未观察组。
import gpboost as gpb
import numpy as np
import sklearn.datasets as datasets
import time
import pandas as pd# Simulate data
ntrain = 5000 # number of samples for training
n = 2 * ntrain # combined number of training and test data
m = 500 # number of categories / levels for grouping variable
sigma2_1 = 1 # random effect variance
sigma2 = 1 ** 2 # error variance
# Simulate non-linear mean function
np.random.seed(1)
X, F = datasets.make_friedman3(n_samples=n)
X = pd.DataFrame(X,columns=['variable_1','variable_2','variable_3','variable_4'])
F = F * 10**0.5 # with this choice, the fixed-effects regression function has the same variance as the random effects
# Simulate random effects
group_train = np.arange(ntrain) # grouping variable
for i in range(m):
group_train[int(i * ntrain / m):int((i + 1) * ntrain / m)] = i
group_test = np.arange(ntrain) # grouping variable for test data. Some existing and some new groups
m_test = 2 * m
for i in range(m_test):
group_test[int(i * ntrain / m_test):int((i + 1) * ntrain / m_test)] = i
group = np.concatenate((group_train,group_test))
b = np.sqrt(sigma2_1) * np.random.normal(size=m_test) # simulate random effects
Zb = b[group]
# Put everything together
xi = np.sqrt(sigma2) * np.random.normal(size=n) # simulate error term
y = F + Zb + xi # observed data
# split train and test data
y_train = y[0:ntrain]
y_test = y[ntrain:n]
X_train = X.iloc[0:ntrain,]
X_test = X.iloc[ntrain:n,]学习和做出预测 (Learning and making predictions)
The following code shows how one trains a model and makes predictions. As can be seen below, the learned variance parameters are close to the true ones. Note that when making predictions, one can make separate predictions for the mean function F(X) and the random effects Zb.
以下代码显示了如何训练模型并进行预测。 如下所示,学习的方差参数接近真实参数。 注意,进行预测时,可以对均值函数F(X)和随机效应Zb进行单独的预测。
# Define and train GPModel
gp_model = gpb.GPModel(group_data=group_train)
# create dataset for gpb.train function
data_train = gpb.Dataset(X_train, y_train)
# specify tree-boosting parameters as a dict
params = { 'objective': 'regression_l2', 'learning_rate': 0.1,
'max_depth': 6, 'min_data_in_leaf': 5, 'verbose': 0 }
# train model
bst = gpb.train(params=params, train_set=data_train, gp_model=gp_model, num_boost_round=32)
gp_model.summary() # estimated covariance parameters
# Covariance parameters in the following order:
# ['Error_term', 'Group_1']
# [0.9183072 1.013057 ]
# Make predictions
pred = bst.predict(data=X_test, group_data_pred=group_test)
y_pred = pred['fixed_effect'] + pred['random_effect_mean'] # sum predictions of fixed effect and random effect
np.sqrt(np.mean((y_test - y_pred) ** 2)) # root mean square error (RMSE) on test data. Approx. = 1.25参数调整 (Parameter tuning)
A careful choice of the tuning parameters is important for all boosting algorithms. Arguably the most important tuning parameter is the number of boosting iterations. A too large number will often result in over-fitting in regression problems and a too small value in “under-fitting”. In the following, we show how the number of boosting iterations can be chosen using cross-validation. Other important tuning parameters include the learning rate, the tree-depth, and the minimal number of samples per leaf. For simplicity, we do not tune them here but use some default values.
仔细选择调整参数对于所有升压算法都很重要。 可以说,最重要的调整参数是加速迭代的次数。 数量太大通常会导致回归问题过度拟合,而“欠拟合”值太小。 在下面,我们展示了如何使用交叉验证来选择增强迭代的次数。 其他重要的调整参数包括学习率,树深度和每片叶子的最少样本数。 为简单起见,我们在这里不对其进行调整,而是使用一些默认值。
# Parameter tuning using cross-validation (only number of boosting iterations)
gp_model = gpb.GPModel(group_data=group_train)
cvbst = gpb.cv(params=params, train_set=data_train,
gp_model=gp_model, use_gp_model_for_validation=False,
num_boost_round=100, early_stopping_rounds=5,
nfold=4, verbose_eval=True, show_stdv=False, seed=1)
best_iter = np.argmin(cvbst['l2-mean'])
print("Best number of iterations: " + str(best_iter))
# Best number of iterations: 32特征重要性和部分依赖图 (Feature importance and partial dependence plots)
Feature importance plots and partial dependence plots are tools for interpreting machine learning models. These can be used as follows.
特征重要性图和偏相关图是解释机器学习模型的工具。 这些可以如下使用。
# Plotting feature importances
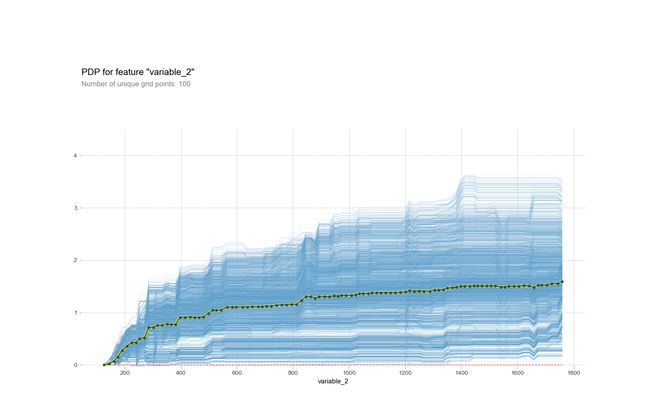
gpb.plot_importance(bst)Univariate partial dependence plots
单变量偏相关图
from pdpbox import pdp
# Single variable plots
pdp_dist = pdp.pdp_isolate(model=bst, dataset=X_train,
model_features=X_train.columns,
feature='variable_2',
num_grid_points=100)
pdp.pdp_plot(pdp_dist, 'variable_2', plot_lines=True)Multivariate partial dependence plots
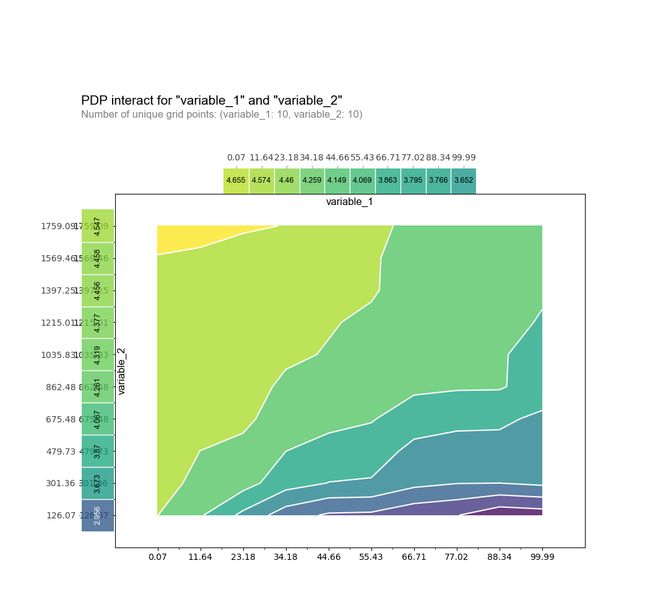
多元偏相关图
# Two variable interaction plot
inter_rf = pdp.pdp_interact(model=bst, dataset=X_train, model_features=X_train.columns,
features=['variable_1','variable_2'])
pdp.pdp_interact_plot(inter_rf, ['variable_1','variable_2'], x_quantile=True, plot_type='contour', plot_pdp=True)SHAP值 (SHAP values)
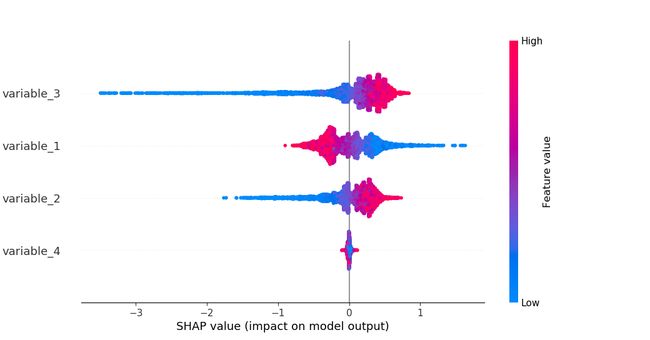
SHAP values and dependence plots are another important tool for model interpretation. These can be created as follows.
SHAP值和依赖性图是模型解释的另一个重要工具。 这些可以如下创建。
Edit: this is currently not yet fully supported by the shap Python package. It should be available soon (hopefully in the next days, see here for the current status). In the meantime, you have to copy-paste a few lines of code to your shap Python package. Just go to the location where your python packages are and add these green marked lines of code to the shap/tree_explainers/tree.py file.
编辑:shap Python软件包目前尚未完全支持此功能。 它应该很快就可用(希望在接下来的几天中,请参阅 此处 了解当前状态)。 同时,您必须将几行代码复制粘贴到您的shap Python包中。 只需转到python包所在的位置,然后将 这些 带有 绿色标记的代码行 添加 到shap / tree_explainers / tree.py文件即可。
import shap
shap_values = shap.TreeExplainer(bst).shap_values(X_test)
shap.summary_plot(shap_values, X_test)
shap.dependence_plot("variable_2", shap_values, X_test)与替代方法的比较 (Comparison to alternative approaches)
In the following, we compare the GPBoost algorithm to several existing approaches using the above simulated data. We consider the following alternative approaches:
接下来,我们使用上述模拟数据将GPBoost算法与几种现有方法进行比较。 我们考虑以下替代方法:
A linear mixed effects model (‘Linear_ME’) where F(X) is a linear function
线性混合效果模型('Linear_ME') ,其中F(X)是线性函数
Standard gradient tree-boosting ignoring the grouping structure (‘Boosting_Ign’)
标准梯度树增强忽略分组结构('Boosting_Ign')
Standard gradient tree-boosting including the grouping variable as a categorical variables (‘Boosting_Cat’)
标准梯度树增强功能,包括将分组变量作为分类变量('Boosting_Cat')
Mixed-effects random forest (‘MERF’) (see here and Hajjem et al. (2014) for more information)
混合效应随机森林(“ MERF”) (有关更多信息,请参见此处和Hajjem等(2014) )
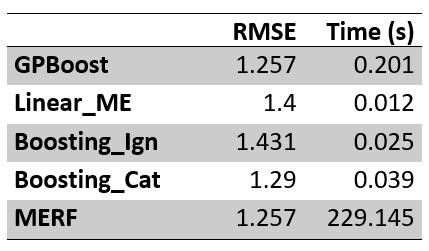
We compare the algorithms in terms of predictive accuracy measured using the root mean square error (RMSE) and computational time (clock time in seconds). The results are shown in the table below. The code for producing these results can be found below in the appendix.
我们根据均方根误差(RMSE)和计算时间(以秒为单位的时钟时间)测得的预测准确性比较算法。 结果如下表所示。 产生这些结果的代码可以在下面的附录中找到。
Comparison of GPBoost and alternative approaches. GPBoost与替代方法的比较。We see that GPBoost and MERF perform clearly best (and almost equally well) in terms of predictive accuracy. Further, the GPBoost algorithm is approximately 1000 times faster than the MERF algorithm. The linear mixed effects model (‘Linear_ME’) and tree-boosting ignoring the grouping variable (‘Boosting_Ign’) have clearly lower predictive accuracy. Tree-boosting with the grouping variable included as a categorical variable also shows lower predictive accuracy than GPBoost or MERF.
我们看到,就预测准确性而言,GPBoost和MERF的表现明显最佳(并且几乎同样出色)。 此外,GPBoost算法比MERF算法快约1000倍。 线性混合效果模型('Linear_ME')和忽略分组变量的'boosting'(boosting_Ign')具有明显较低的预测准确性。 与GPBoost或MERF相比,将分组变量作为类别变量包括在内的树式提升也显示出较低的预测准确性。
Note that, for simplicity, we do only one simulation run (see Sigrist (2020) for a much more detailed comparison). Except for MERF, all computations are done using the GPBoost library version 0.2.1 compiled with MSVC version 19.24.28315.0. Further, we use the MERF Python package version 0.3.
请注意,为简单起见,我们仅进行一次模拟运行(有关 详细比较, 请参阅 Sigrist(2020) )。 除MERF外,所有计算均使用GPBoost库0.2.1版和MSVC 19.24.28315.0版进行编译。 此外,我们使用MERF Python软件包0.3版。
结论 (Conclusions)
GPBoost allows for combining mixed effects models and tree-boosting. If you apply linear mixed effects models, you should investigate whether the linearity assumption is indeed appropriate. The GPBoost model allows for relaxing this assumption. It may help you to find non-linearities and interactions and achieve higher predictive accuracy. If you are a frequent user of boosting algorithms such as XGBoost and LightGBM and you have categorical variables with potentially high-cardinality, GPBoost (which extends LightGBM) can make learning more efficient and result in higher predictive accuracy.
GPBoost允许将混合效果模型和树加速结合在一起。 如果应用线性混合效应模型,则应调查线性假设是否确实合适。 GPBoost模型允许放宽此假设。 它可以帮助您发现非线性和相互作用,并获得更高的预测准确性。 如果您经常使用诸如XGBoost和LightGBM之类的增强算法,并且您的分类变量具有潜在的高基数,那么GPBoost(扩展了LightGBM)可以使学习 效率更高, 并获得更高的预测准确性。
To the best of our knowledge, the GPBoost library is currently unmatched in terms of computational speed and predictive accuracy. Additional advantages are that GPBoost supports a range of model interpretation tools (variable importance values, partial dependence plots, SHAP values etc.). Further, it also supports other types of random effects such as Gaussian processes in addition to grouped or clustered random effects.
据我们所知,GPBoost库目前在计算速度和预测准确性方面无与伦比。 GPBoost的其他优点是支持多种模型解释工具(可变重要性值,偏相关图,SHAP值等)。 此外,除了分组或聚类的随机效应之外,它还支持其他类型的随机效应,例如高斯过程。
Hopefully, you have found this article useful. More information on GPBoost can be found in the companion article Sigrist (2020) and on github.
希望您发现本文很有用。 有关GPBoost的更多信息,请参见配套文章Sigrist(2020)和github 。
翻译自: https://towardsdatascience.com/tree-boosted-mixed-effects-models-4df610b624cb
面板模型混合效应模型