2021年总务部第一次机器学习培训总结

机器学习的基本概念与建模流程

• 机器学习？
• 分类问题vs回归问题？
• 训练集？测试集？
• 模型训练？模型评估？
• ………

机器学习是现阶段解决很多人工智能问题的主流方法，作为一个独立的方向，正处于高速发展之中。最早的机器学习算法可以追溯到20世纪初，到今天为止，已经过去了100多年。从1980年机器学习称为一个独立的方向开始算起，到现在也已经过去了四十多年。

什么是机器学习？

“一个计算机程序，利用经验E来学习任务T，性能表现为P，如果针对任务T的性能P能随着经验E不断增长，则称为机器学习。

                                                                    ——机器学习教父汤姆·米切尔

“通过不断的喂养数据，让算法变得越来越聪明，就叫做机器学习。”

                                                                     —— 更加通俗的解释

机器学习问题的分类？

• 监督学习：数据拥有标签（“标准答案”）

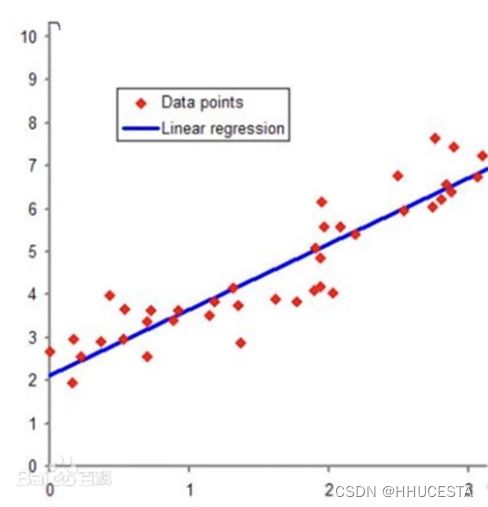
分类问题：将实例数据划分到合适的分类中

回归问题：预测数值型数据，拟合曲线

特性	分类问题	回归问题
输出类型	离散数据	连续数据
目的	寻找决策边界	找到最优拟合
评价方法	精度、混淆矩阵等	SSE等

• 无监督学习：数据没有类别信息，也不会给定目标值
  eg.上次大培训讲过的KNN算法
  

• 判断下列问题属于什么类别

1. 垃圾邮件检测：根据邮箱中的邮件，识别哪些是垃圾邮件，哪些不是。这样的模型，可以程序帮助归类垃圾邮件和非垃圾邮件。
2. 房价预测：根据某地区大量住房的住宅面积、平均房间数、离市中心距离、城镇人均犯罪率、税率等等，预测某个信息一致的房子的价格。
3. 信用卡欺诈检测：根据用户一个月内的信用卡交易，识别哪些交易是该用户操作的，哪些不是。这样的决策模型，可以帮助程序退还那些欺诈交易。
4. 鸢尾花类型判断：根据鸢尾花的花萼长度、花萼宽度、花瓣长度、花瓣宽度，判断一朵鸢尾花属于山鸢尾、变色鸢尾还是维吉尼亚鸢尾。
5. “猜你喜欢”、短视频推送
   有标签也可以自己不要标签，因此两者并不绝对

机器学习基本流程

Step1：使⽤⼤量和任务相关的数据集来训练模型；
Step2：通过模型在数据集上的误差不断迭代训练模型，得到对数据集拟合合理的模型；
Step3：将训练好调整好的模型应⽤到真实的场景中；

数据预处理 → 划分为训练集和测试集 → 用训练集训练模型 → 将模型应用在测试集数据上 → 对比预测结果与真实结果 → 不断反馈直到结果较接近 → 将模型应用在未知数据上
通常将数据集的70%~85%作为训练集，剩余部分作为测试集

• 机器在学习中“变聪明”的本质：反馈机制
  
  笨一点，错的多，再改正就好啦~

朴素贝叶斯算法

• 解决有监督、分类问题

原理：引入贝叶斯公式

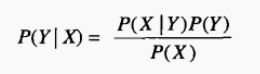
eg.（简单数学题）小明要从A地赶往B地，有两种方式，坐高铁和坐飞机，其中，他选择高铁的概率为60%，选择飞机的概率为40%，若坐高铁，他迟到的概率为10%，若坐飞机，他迟到的概率为25%。已知小明最终迟到了，请问他坐高铁前往B地的概率为多少？

• C1：坐高铁
• X/C1：坐高铁时迟到
• C2：坐飞机
• X/C2：坐飞机时迟到
• X：迟到
• C1/X：迟到了，是坐高铁来的
• 已知P(C1)、P(C2)、P(X/C1)、P(X/C2)，且P(X)可求，因此P(C1/X)可求

实例引入：

详情参考视频 “朴素贝叶斯：最通俗易懂的解释”

代码实现

Scikit-Learn实现

高斯朴素贝叶斯：sklearn.naive_bayes.GaussianNB(priors=None)**

鸢尾花数据集
 
在Sklearn机器学习包中，集成了各种各样的数据集，包括前面的糖尿病数据集，这里引入的是鸢尾花卉（Iris）数据集，它是很常用的一个数据集。鸢尾花有三个亚属，分别是山鸢尾（Iris-setosa）、变色鸢尾（Iris-versicolor）和维吉尼亚鸢尾（Iris-virginica）。
 
该数据集一共包含4个特征变量，1个类别变量。共有150个样本，iris是鸢尾植物，这里存储了其萼片和花瓣的长宽，共4个属性，鸢尾植物分三类。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
gnb = GaussianNB()
y_pred = gnb.fit(X_train, y_train).predict(X_test)
print("Number of mislabeled points out of a total %d points : %d"% (X_test.shape[0], (y_test != y_pred).sum()))

底层代码实现：

0引入numpy库（用于处理矩阵）

import numpy as np

1 建立文本数据

文本数据用一个个对象组成，一个对象是由若干单词组成，每个对象对应一个确定的类别。

代码如下：

# 创建文本数据集
def loadDataList():
    postingList = [ ['my','dog','has','flea','problems','help','please'],
                    ['maybe','not','take','him','to','dog','park','stupid'],
                    ['my','dalmation','is','so','cute','I','love','him'],
                    ['stop','posting','stupid','worthless','garbage'], 
                    ['mr','licks','ate','my','steak','how','to','stop','him'], 
                    ['quit','buying','worthless','dog','food','stupid']] 
    classVec = [0,1,0,1,0,1] 
    return postingList,classVec

2 对文本数据的处理

从文本数据中提取出训练样本的属性集，这里是属性集是由单词组成的词汇集。

代码如下：

# 提取训练集的所有词
def createVocabList(dataSet):
    vocabSet = set([])
    for document in dataSet :
        vocabSet = vocabSet | set(document)  # 两个集合的并集
    return list(vocabSet)

这里利用集合的性质对数据集提取不同的单词，函数 createVocabList() 返回值是列表类型。

3 对词汇集转化成数值类型

因为单词的字符串类型无法参与到数值的计算，因此把一个对象的数据由词汇集中的哪些单词组成表示成：0 该对象没有这个词，1 该对象有这个词。

代码如下：

# 根据类别对词进行划分数值型的类别
def setOfWords2Vec(vocabList, inputSet):
    returnVec = [0]*len(vocabList)
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)] = 1
        else :
            print("the word : %s is not in my Vocabulary!" % word)
    return returnVec

参数 vocabList 是词汇集，inputSet 是对象的数据，而返回值是由词汇集的转换成 0 和 1 组成的对象单词在词汇集的标记。

4 朴素贝叶斯分类器的训练函数

这里说明一下，训练样本是postingList 列表数据，属性集是词汇集，类标号是classVec 列表数据。在编写代码时考虑到对象的单词在词汇集中占有率比较低，会造成词汇集转化时有大量的 0 组成，同时又会造成条件概率大量为 0 ；又有计算真实概率值普遍偏小，容易造成下溢出。因此，代码对计算条件概率时进行转换，但不影响条件概率的大小排序，也就不会影响朴素贝叶斯的使用。

代码如下：

'''
求贝叶斯公式中的先验概率 pAbusive ,条件概率 p0Vect、p1Vect；函数中所求的概率值
是变形值，不影响贝叶斯的核心思想：选择具有最高概率的决策
'''
def trainNB0(trainMatrix, trainCategory):
    numTrainDocs = len(trainMatrix)  # 样本中对象的个数
    numWords = len(trainMatrix[0]) # 样本中所有词的集合个数
    pAbusive = sum(trainCategory) / float(numTrainDocs) # 对类别只有两种的先验概率计算
    # 对所有词在不同的类别下出现次数的初始化为1，为了防止计算条件概率出现为0
    p0Num = np.ones(numWords)
    p1Num = np.ones(numWords)
    # 对不同类别出现次数的初始化为2，词的出现数初始数为1的情况下，增加分母值避免概率值大于1
    p0Denom = 2.0
    p1Denom = 2.0
    for i in range(numTrainDocs):  # 遍历所有对象
        if trainCategory[i] == 1: # 类别类型的判断
            p1Num += trainMatrix[i]  # 对所有词在不同的类别下出现次数的计算
            p1Denom += sum(trainMatrix[i]) # 对不同类别出现次数的计算
        else:
            p0Num += trainMatrix[i] # 对所有词在不同的类别下出现次数的计算
            p0Denom += sum(trainMatrix[i]) # 对不同类别出现次数的计算
    p1Vect = np.log ( p1Num / p1Denom)  # 条件概率,用对数的形式计算是为避免概率值太小造成下溢出
    p0Vect = np.log (p0Num / p0Denom)   # 条件概率,用对数的形式计算是为避免概率值太小造成下溢出
    return p0Vect, p1Vect, pAbusive

5 朴素贝叶斯的分类函数

根据先验概率和条件概率对不同类别的后验概率进行计算，并选取后验概率最大的类别作为朴素贝叶斯预测结果值。

代码如下：

# 计算后验概率，并选择最高概率作为预测类别
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
    p1 = sum(vec2Classify * p1Vec ) + np.log(pClass1) # 对未知对象的单词的每一项的条件概率相加（对数相加为条件概率的相乘）
    p0 = sum(vec2Classify * p0Vec ) + np.log(1.0-pClass1 ) # 后面加上的一项是先验概率
    if p1 > p0:
        return 1
    else :
        return 0

6 测试样本的预测

通过朴素贝叶斯算法给出两个未知类别的对象预测其类别。

代码如下：

# 对侮辱性语言的测试
def testingNB():
    listOposts, listClasses = loadDataList() # 训练样本的数据，listOposts 为样本，listClasses 为样本的类别
    myVocabList = createVocabList(listOposts) # 样本的词汇集
    trainMat = [] # 对样本的所有对象相关的单词转化为数值
    for postinDoc in listOposts :
        trainMat.append(setOfWords2Vec(myVocabList,postinDoc))
    p0V, p1V, pAb = trainNB0(np.array(trainMat),np.array(listClasses)) # 样本的先验概率和条件概率
    testEntry = ['love','my','dalmation','love'] # 未知类别的对象
    thisDoc = np.array(setOfWords2Vec(myVocabList ,testEntry ) ) # 对未知对象的单词转化为数值
    print(testEntry ,'classified as : ',classifyNB(thisDoc, p0V,p1V,pAb)) # 对未知对象的预测其类别
    testEntry = ['stupid','garbage'] # 未知类别的对象
    thisDoc = np.array(setOfWords2Vec(myVocabList ,testEntry )) # 对未知对象的单词转化为数值
    print(testEntry, 'classified as : ', classifyNB(thisDoc, p0V, p1V, pAb)) # 对未知对象的预测其类别

7运行

testingNB()

其运行结果图：

对象 [‘love’,‘my’,‘dalmation’,‘love’] 由直观可知，其类别是非侮辱性词汇，与预测结果（0 代表正常语言）相同；对象 [‘stupid’,‘garbage’] 类别是侮辱性词汇，与预测结果（1 代表侮辱性语言）相同，说明朴素贝叶斯算法对预测类别有效。

算法优缺点总结

优点：

朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。

对缺失数据不太敏感，算法也比较简单，常用于文本分类。

分类准确度高，速度快

缺点：

需要知道先验概率P(F1,F2,…|C)，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。