「Python数据分析系列」20. 聚类分析
来源 | Data Science from Scratch, Second Edition
作者 | Joel Grus
译者 | cloverErna
校对 | gongyouliu
编辑 | auroral-L
全文共4225字,预计阅读时间30分钟。
第二十章 聚类分析
1. 原理
2. 模型
3. 示例:聚会
4. 选择聚类数目k
5. 示例:对色彩进行聚类
6. 自下而上的分层聚类
7. 延伸学习
使吾辈得以类聚者,热情而非疯狂也。
——罗伯特 · 赫里克
本书中的大多数算法都是所谓的监督学习方法,因为它们都是以一组标注过的数据作为起点的,并且在此基础上为新的、未标注过的数据做出预测。然而,本章介绍的聚类分析却是一种无监督学习方法,也就是说,它可以利用完全未经标注的数据(也可以使用标注过的数据,但我们忽略这些标签)进行工作。
1. 原理
每当你观察某些数据源时,很可能会发现数据会以某种形式形成聚类(cluster)。例如,展示百万富翁居住地的数据集中,数据点很可能在贝弗利山和曼哈顿等地方形成聚类。而在展示人们每周工作时间(以小时为单位)的数据集中,数据则很可能聚集在 40 附近(并且,如果这些数据来自法律规定人们每周至少工作 20 个小时的国家的话,那么这些数据很可能就会聚集在 19 左右。)对于登记选民的人口统计的数据集,则可能形成多种集群 (例如“足球妈妈”“无聊的退休人员”“待业千禧”等),这些群体正是民意调查和政治顾问所要密切关注的。
与之前见到的问题不同,这种问题通常没有“正确”的聚类。一个可选的聚类方案是将某些“待业千禧”与“大学毕业生”分为一伙,而将另一些“待业千禧”与“啃老族”分为一组。当然,很难说哪种方案肯定比其他方案要好,但是,对于每一种方案而言,都可以按照自己的“优良聚类”标准不断进行优化。
此外,这些聚类本身无法对自己进行标注。要想标注的话,你必须考察每个聚类中的底层数据。
2. 模型
对于我们来说,每一个输入都是 d 维空间中的一个向量(跟以前一样,我们还是使用数字列表来表示向量)。我们的目标是识别由类似的输入所组成的聚类,(有时)还要找出每个聚类的代表值。
例如,每个输入可以是博客文章的标题(我们可以设法用数字向量来表示它),那么在这种情况下,我们的目标可能是对相似的文章进行聚类,也可能是为了了解用户都在写什么博客内容。或者,假设我们有一张包含数千种(红、绿、蓝)颜色的图片,但是我们需要一个10 色版本来进行丝网印刷。这时,聚类分析不仅可以帮助我们选出 10 种颜色,并且还能将“色差”控制在最小的范围之内。
k-均值算法(k-means)是一种最简单的聚类分析方法,它通常需要首先选出聚类 k 的数目,然后把输入划分为集合 S1,…,Sk,并使得每个数据到其所在聚类的均值(中心对象)的距离的平方之和最小化。
由于将 n 个点分配到 k 个聚类的方法非常多,所以寻找一个最优聚类方法是一件非常困难的事情。一般情况下,为了找到一个好的聚类方法,我们可以借助于迭代算法:
1. 首先从 d 维空间中选出选择 k 个数据点作为初始聚类的均值(即中心)。
2. 将每个点分配给它最接近的聚类中心。
3. 如果所有数据点都不再被重新分配,那么就停止并保持现有聚类。
4. 如果仍有数据点被重新分配,则重新计算均值,并返回到第 2 步。
利用第 4 章中学过的 vector_mean 函数,可以轻松创建如下所示的类来完成上述工作。
首先,我们将创建一个辅助函数,它度量两个向量的分量有多少不一样。我们将使用此方法来跟踪我们的训练进度:
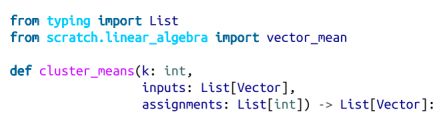
我们还需要一个函数,它给定一些向量和它们所属的聚类,来计算聚类的均值。可能存在一种情况,某个聚类没有向量分配给图。因为我们不能计算空集合的均值,所以在这种情况下,我们将随机选择其中一个点作为该聚类的“均值”:
现在我们已经准备好编码我们的聚类算法了。像往常一样,我们将使用tqdm跟踪我们的进度,但这里我们不知道需要多少迭代,因此我们使用itertools.count,它创建无限迭代,并在完成后返回:
下面让我们来看看其中的原理。
3. 示例:聚会
为了庆祝 DataSciencester 的发展壮大,用户回馈部门的副总决定针对你家乡的用户组织几场私人聚会,并赞助啤酒、披萨和 DataSciencester T 恤。由于你了解所有当地用户的住址(如图 20-1),所以他想让你来选择聚会的地点,以方便大家的参与。
图20-1. 你的家乡用户的位置
根据你的查看方式,你可能会看到两到三个集群。(视觉上很容易,因为数据只是二维的。如果维度更高,就很难从视觉上感知了。)
首先想象一下,她有足够的预算来参加三次聚会。你进入电脑并试试:
你可以在[-44、5]、[-16、-10]和[18,20]为中心找到三个集群,并在这些位置附近的聚会场所(图20-2)。
图20-2. 用户位置分为三个聚类
你向副总裁展示你的结果,副总裁告诉你,现在她只有足够的预算参加两次聚会。“没问题,”你说:
如图20-3所示,一个聚会应该仍然在[18,20]附近,但现在另一个聚会应该接近[-26,-5]。
图20-3. 用户位置分为两个聚类
4. 选择聚类数目k
在前一个例子中,聚类数目 k 的选择是由外部因素决定的,我们无法控制。但是通常情况下,事情并非如此。k 的选择方法可谓五花八门,一个比较易于理解的方法是以误差(即每个数据点到所在聚类的中心的距离)的平方之和作为 k 的函数,画出该函数的图像,并在其“弯曲”的地方寻找合适的取值:
我们可以应用于我们之前的例子:
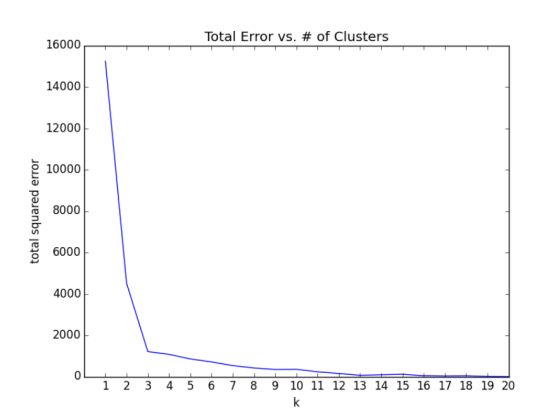
看图20-4,这种方法与我们最初的视觉判断一致,即三个是“正确”的聚类数。
图20-4. 选择合适的k
5. 示例:对色彩进行聚类
负责周边产品的副总设计了一款美观的 DataSciencester 便签,希望你能够在聚会上分发给用户。令人遗憾的是,你的便签打印机功能有限,每张便签上面最多只能打出五种色彩。同时,由于负责美术的副总正在休假,因此,负责周边产品的副总向你咨询能否将其设计改为只包含五种颜色。
我们知道,计算机图像可以表示为像素的二维阵列,其中每个像素本身就是一个三维向量(red, green, blue),代表了该像素的颜色。
为了得到图像的五色版本,我们需要执行下列步骤:
1. 选择五种颜色。
2. 给每个像素从中挑选一种颜色。
事实上,这个工作非常适合用 k-means 算法来做,因为该算法能够将像素划分为红 - 绿 - 蓝空间中的五个聚类。之后,我们只要将这些聚类中的像素用其中间色来重新着色就可以了。
首先,我们需要设法将图像加载到 Python 中。事实上,这可以借助 matplotlib 来实现:
然后我们就可以只使用matplotlib.image.imread:了
实际上,img 在幕后是作为一个 NumPy 数组来处理的,不过就这里来说,我们可以将其视为以列表为元素的列表所组成的列表。
这里,img[i][j] 表示第 i 行第 j 列的像素,并且每个像素都由一个取值范围介于 0 和 1 之间的 [red, green, blue] 数字列表来指定其颜色:
特别是,我们可以将所有像素放到一个扁平化的列表中,如:
然后将其送入我们的聚类模型:
一旦完成,我们得到了一张具有相同格式的新图像:
接下来,我们就可以通过 plt.imshow() 来显示该图像了:
要在黑白书籍中很难显示颜色的结果,但图20-5显示了全彩色图片的灰度版本,以及使用此过程将其减少到五种颜色的输出。
图 20-5:原始图像以及利用 5-means 去色后的效果
6. 自下而上的分层聚类
另一种聚类方法是采用自下而上的方式“生成”聚类,为此,我们可以借助下列方式:
1. 利用每个输入构成一个聚类,当然每个聚类只包含一个元素;
2. 只要还剩余多个聚类,就找出最接近的两个,并将它们合二为一。
最后,我们将得到一个包含所有输入的巨大的聚类。如果我们将合并顺序记录下来,就可以通过拆分的方法来重建任意数量的聚类。举例来说,如果我们想得到 3 个聚类,那么只要撤销最后两次合并就可以了。
我们将使用一种非常简单的方法来表示聚类。首先,我们的数值向量将进入叶(leaf)聚类中,这时我们将其表示为NamedTuples:
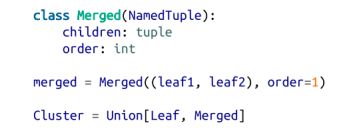
我们将使用这些来逐步合并聚类,并将其表示为NamedTuples:
注意
这是另一种Python的类型注释让我们失望的况。你希望将hintMerged.children键入Tuple[cluster,cluster],但mypy不允许使用这样的递归类型。
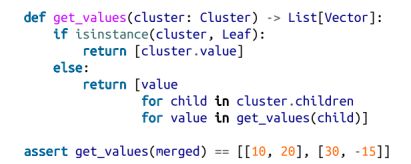
我们将稍微讨论合并顺序,但首先创建一个辅助函数,递归地返回(可能合并的)聚类中包含的所有值:
为了合并相距最近的聚类,我们需要明确聚类之间的距离的概念。为此,我们将使用两个聚类的元素之间的最小距离,据此将两个挨得最近的聚类合并(但有时会产生巨大的链式聚类,但是聚类之间却挨得不是很紧)。如果想得到紧凑的球状聚类,可使用最大距离,而不是最小距离,因为使用最大距离合并聚类时,它会尽力将两者塞进一个最小的球中。实际上,这两种距离都很常用,就像平均距离也很常用一样:
我们将借助合并次序slot来跟踪合并的顺序。这个数字越小,表示合并的次序越靠后。这意味着,当我们想分拆聚类的时候,可以根据合并次序的值,从最小到最大依次进行。由于叶聚类不是合并而来的(这意味着无需分拆它们),因此,我们将它们合并次序的值规定为无穷大:
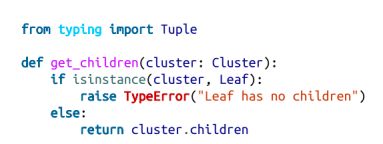
同样,由于Leaf聚类没有children,我们将为此创建并添加一个辅助函数:
现在我们可以创建聚类算法了:
其使用方式非常简单:
这将得到一个聚类,简单表示如下:
顶部的数字表示“合并顺序”。“由于我们有20个输入,所以需要19个合并才能到达这个集群。第一个合并通过组合叶子[19,28]和[21,27]创建了集群18。并且最后一次合并创建了集群0。
如果只需要两个集群,可以在第一个分叉(“0”)拆分,创建一个有6个点的聚类和余下其它点构成的聚类。对于三个聚类,你将继续使用第二个分叉(“1”),这表示将第一个聚类拆分为([19,28]、[21,27]、[20,23]、[26,13])和([11,15]、[13,13])。以此类推。
不过,一般来说,我们不想费眼睛看这样令人讨厌的文本表示。相反,让我们编写一个函数,通过执行适当数量的“逆合并”来生成任意数量的聚类:
例如,如果我们想生成三个聚类,我们只需要:
我们可以很容易地打印出来:
这给出的结果与k-均值有非常不同的结果,如图20-6所示。
图20-6. 三个自下而上的聚类,使用最小距离
如前所述,这是因为在cluster_distance中使用min往往会给出类似链的聚类。如果我们使用最大值(它给出了紧密的聚类),它看起来与3-means的结果相同(图20-7)
注意
以上的 bottom_up_clustering 的实现代码相对来说已经很简单了,但是计算效率依然低得吓人。特别是,在每一步它都要重新计算每对输入之间的距离。更有效的实现方法是,预先算出每对输入之间的距离,然后在 cluster_ distance 里面进行查找。一个真正高效的实现方法可能还需要存储上一步的cluster_distance。
图 20-7:利用最大距离得到的3个自下而上的聚类
7. 延伸学习
• scikit-learn 库中提供了一个单独的模块 sklearn.cluster(https://scikit-learn.org/stable/modules/clustering.html),其中含有多个聚类算法,包括 KMeans 和 Ward 分级聚类算法(该算法使用了不同的聚类合并规则)。
• Scipy(https://www.scipy.org/)模块也有两个聚类模型,即 scipy.cluster.vq(它使用 k- means算法)模型和 scipy.cluster.hierarchy(它使用多种层次聚类算法)模型。